Rep:Mod:jyg11physcomp

The Cope Rearrangement

Introduction

The Cope Rearrangement is a concerted pericyclic reaction which involves the 3,3-sigmatropic rearrangement of 1,5-dienes. The reaction is thought to occur via either a “chair” or “boat” transition state, which we will investigate in this exercise.

Figure 1: The Cope rearrangement of 1,5-hexadiene

Optimising the Reactants and Products

First, a molecule of 1,5-hexadiene was drawn in GaussView with a dihedral angle of 180° between C2-C3-C4-C5. This was optimised at the HF/3-21G level of theory. The optimised molecule was also symmetrised, and when compared with the reference table was shown to be the anti2 conformer of 1,5-hexadiene.

A second molecule of 1,5-hexadiene was constructed, this time with a dihedral angle of 60° between C2-C3-C4-C5. This was also optimised at the HF/3-21G level of theory and symmetrised – in doing so, the dihedral angle was altered to 63.67°. The gauche4 conformer was found.

The table below shows the information obtained from optimisation and symmetrising the anti2 and gauche4 conformers. Other conformers at energy minima were also found (see Appendix 1).

Table 1: Results from the optimisation and symmetrising of the initial antiperiplanar and gauche conformations

	gauche4	anti2
Structure
Point Group	C2	Ci
Energy (Ha) HF/3-21G	-231.6915303	-231.6925353
Energy (kcal/mol)	-145388.5205	-145389.1511

It can be seen from this table that the anti2 conformer is lower in energy than the gauche4 conformer by roughly 0.63 kcal/mol. This can be attributed to the proximity of the groups; in gauche4 they are much closer to each other than in anti2 and so may have a slightly larger steric repulsion.

Next, the anti2 conformer was optimised at the B3LYP/6-31G level of theory. The B3LYP method allows us to calculate the energy of many-electron systems, and the more specific 6-31G basis set gives a better approximation of the geometry, and therefore the energy. We also took the p and d orbitals into account to give a more refined minimum. The two optimisations – one at HF/32-1G and the other at B3LYP/6-31G – are shown in the figure below. The geometry of the structure has changed negligibly, but there is an energy difference of 1832 kcal/mol, where the B3LYP/6-31G method gives the lower energy conformer.

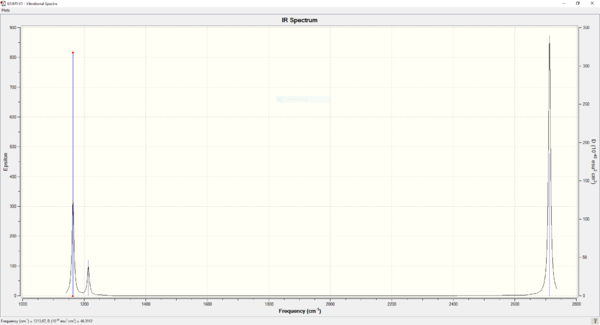
The newly optimised anti2 structure was then subjected to a frequency calculation, which yielded a series of vibrational modes. A few of these modes are shown below, as well as the predicted infrared spectrum of 1,5-hexadiene.

Vibrational mode 13, corresponding to the peak at 940 cm^-1

Vibrational mode 32, corresponding to the peak at 1734 cm^-1

Vibrational mode 36, corresponding to the peak at 3081 cm^-1

Predicted infrared spectrum of 1,5-hexadiene.

Optimising the Chair and Boat Transition Structures

The Chair Transition State

A CH₂CHCH₂ fragment was optimised to the H2/32-1G level of theory, then duplicated to mimic the positions of the atoms in a chair conformation. The distances between C1/C2 and C3/C4 were 2.20Å and 2.21Å respectively.

The "guess" chair structure built with optimised CH₂CHCH₂ fragments

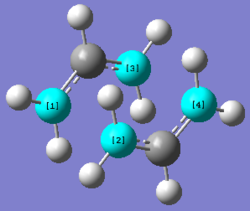
Berny Transition State Method

Using the Berny TS method, an opt+freq calculation was run on this guess structure, with the additional keywords opt=noeigen to prevent imaginary frequencies affecting the calculation. The optimised structure and its corresponding imaginary frequency are shown below. The imaginary frequency corresponding to the Cope rearrangement was found to be 817.8 cm^-1

The optimised chair transition state structure using the Berny method.

Frozen Coordinate Transition State Method

The chair transition state could also be optimised a second way - using the frozen coordinate method. Using the same guess structure, the C1/C2 and C3/C4 atom pairs were "frozen" at a fixed distance using the Redundant Coordinate Editor, in this case at the 2.20Å and 2.21Å specified above. The method used was a regular optimisation and not the Berny method.

Next the second derivatives of the optimisation were measured. The Redundant Coordinate Editor was used again to specify the C1/C2 and C3/C4 atom pairs, and the structure optimised. A comparison between the chair transition structures obtained using the Berny and frozen coordinate methods is shown below.

The optimised chair transition state structures using the Berny (left) and frozen coordinate (right) methods.

The Boat Transition State

The boat transition state was optimised using the QST2 method instead of the Berny or frozen coordinate methods, because it is possible to specify the start and end structures of a reaction. The optimised anti2 conformer was used to determine the boat transition structure from.

Using the Atom List, the labels were altered so that the atoms in the product corresponded to the correct atoms in the reactant. The dihedral angles of C2-C3-C4-C5 and C2-C1-C6-C5 were modified to be 0° and the angles of C1-C2-C3 and C4-C5-C5 modified to be 100° (see below). This is to closer approximate the boat transition state.

The labelled anti2 conformers that correspond to the reactant and product molecules, closer approximated to portray the Boat TS.

After running the QST2 method to find the transition state, a boat structure was obtained.

The Boat TS.

After obtaining the chair and boat transition states, an intrinsic reaction coordinate method was employed to find the conformers connected by these transition states. The results of the IRC were also further optimised by 1) running a second IRC, this time with 100 points instead of 50, 2) optimising the last point of the initial IRC at the HF/3-21G level of theory and 3) further optimising the minimum found using HF/3-21G, using the B3LYP/6-31G level of theory. The results are shown below.

'	Energy (Ha) HF/3-21G	RMS Grad. Norm	Energy (Ha) B3LYP/6-31G* (opt+freq)	Difference in Energy
ChairTS_guess1_berny1_IRC3	-231.69157904	0.00015225
ChairTS_guess1_berny1_IRC3_furtherIRC100	-231.69157888	0.00015227
ChairTS_guess1_berny1_IRC3_furtheroptmin	-231.69166702	0.00000474	-234.62587725	2.93421023
ChairTS_guess1_frozen1_deriv_IRC	-231.69166702	0.00000485
ChairTS_guess1_frozen1_deriv_IRC_furtherIRC100	-231.69166702	0.00000485
ChairTS_guess1_frozen1_deriv_IRC_furtheroptmin	-231.69166702	0.00000484	-234.62585489	2.93418787
Boat_attempt1_nonfailQST2_IRC	-231.68298131	0.00010257
Boat_attempt1_nonfailQST2_IRC_furtherIRC100	-231.68298100	0.00010259
Boat_attempt1_nonfailQST2_IRC_furtheroptmin	-231.68302549	0.00000842	-234.61830271	2.93527722

These energies correspond to the following conformers:

Appendix 1

Conformer	Structure	Point Group	Energy (Ha) HF/3-21G	Relative energies (kcal/mol)
gauche1		C2	-231.6877161	3.10
gauche2		C2	-231.691667	0.62
gauche3		C1	-231.6926611	0.00
gauche4		C2	-231.6915303	0.71
gauche5		C1	-231.6896157	1.91
gauche6		C1	-231.6891602	2.20
anti1		C2	-231.6926024	0.04
anti2		Ci	-231.6925353	0.08
anti3		C2h	-231.6890707	2.25
anti4		C1	-231.6909706	1.06

The Diels Alder Cycloaddition

Introduction

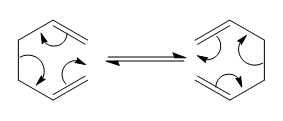
The Diels Alder reaction is also a concerted pericyclic reaction, under the cycloaddtion category. It is particularly facile between conjugated dienes and an alkene (also known as a dienophile) to give a cyclohexene, and demonstrates good control over stereochemistry and regiochemistry. The reaction is commonly used to decorate cyclohexene rings, by use of substituted starting materials, as shown in Figure 1.