Rep:Mod:jwy17

NH₃

Link to .log file https://wiki.ch.ic.ac.uk/wiki/images/c/c2/JY_OPT_NH3_1.LOG

Bond Length

Each N-H = 1.01798 Angstrom

Bond Angle

H-N-H angle = 105.741 degrees

nh3 optimisation
File Name	JY_opt_nh3_1
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.55776873	 a.u.
RMS Gradient Norm	0.00000485	 a.u.
Imaginary Freq	0
Dipole Moment	1.8466	 Debye
Point Group	C3V

          Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986286D-10
 Optimization completed.
    -- Stationary point found.

NH3

Vibrations

-Using the 3N-6 rule, the expected number of vibrational modes is 6, which is true based on the Gaussian program.

-There are 2 pairs of vibrational modes that are degenerate.

-3 vibrational modes (the first three in the above picture) are bending vibrations and 3 other are stretching vibrations.

-2 of these vibrational modes are highly symmetric

-1089.54 HZ is the 'umbrella' mode.

-4 bands should appear because there are 2 pairs of degenerate vibrational modes.

Charge Distribution Over NH₃ Molecule

we would expect the N atom to have the partial negative charge of -1.125 and H atams to have partial positive charge of +0.375. As the N atom is much more electronegative than the 3 H atoms, it 'pulls' electron density towards itself and equally from all 3 H atoms, which is why the magnitude of charge on N is 3 times larger than the Hs'.

HOMO and LUMO of NH₃

The HOMO of NH₃ is the deconstructive overlapping of the nitrogen's s orbital and the Hs' s orbitals all in the same phase. Hence, it is an antibonding molecular orbital.

H₂ and N₂

H₂

Link to .log file https://wiki.ch.ic.ac.uk/wiki/images/2/2e/JY_OPT_H2_1.LOG

       Item               Value     Threshold  Converged?
 Maximum Force            0.000066     0.000450     YES
 RMS     Force            0.000066     0.000300     YES
 Maximum Displacement     0.000087     0.001800     YES
 RMS     Displacement     0.000123     0.001200     YES
 Predicted change in Energy=-5.726834D-09
 Optimization completed.
   -- Stationary point found.

File Name	JY_opt_h2_1
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-1.17853935	 a.u.
RMS Gradient Norm	0.00003809	 a.u.
Imaginary Freq	0
Dipole Moment	0.0000	 Debye
Point Group	D*H

H2

N₂

Link to .log file https://wiki.ch.ic.ac.uk/wiki/images/4/4b/JY_OPT_N2_1.LOG

        Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.401111D-13
 Optimization completed.
   -- Stationary point found.

File Name	JY_opt_n2_1
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-109.52412868	 a.u.
RMS Gradient Norm	0.00000060	 a.u.
Imaginary Freq	0
Dipole Moment	0.0000	 Debye
Point Group	D*H

N2

Calculation for energy for Haber-Bosch reaction

E(NH3) = -56.55776873 a.u.

2*E(NH3) = -113.11553746 a.u.

E(N2) = -109.52412868 a.u.

E(H2) = -1.17853935 a.u.

3*E(H2)= -3.53561805 a.u.

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579073 a.u.

-0.05579073/2 a.u. = -73.24 kJ/ mol (2d.p.)

CF₄

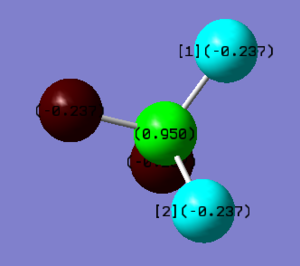
Charge Distribution

The C atom (centre) has a charge of +0.950 and the F atoms (highlighted blue or red) has a -0.237 charge

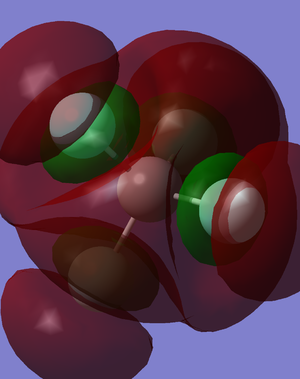
Vibrational modes

There are 2 types vibrations with 3 degenerate levels as the CF₄ molecule vibrates similarly but in 3 different directions. Using the 3N-6 rule, the expected number of vibrational modes is 9, which the computer predicted as well. The are 3 vibrational modes that do not contribute to the infrared spectrum. This suggests that these 3 vibrational mode are symmetrical and do not produce dipole moments.

Molecular orbitals of CF₄

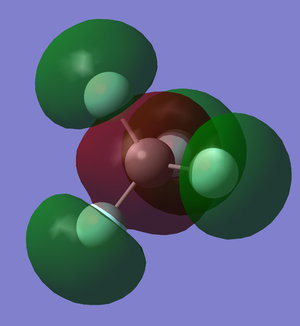
C-F sigma bond

This molecular orbital is formed by the overlap of the 2p orbitals of the fluorine atoms and the 2s orbital of the carbon atom . As this molecular orbital is filled, this molecular orbital contribute 1 bond order to the overall molecule.

2 s orbitals overlap

A very simple molecular orbital formed by the overlapping of the 2s orbitals of each atom. This is not the 1s orbital overlap as the 1s electrons in fluorine are too deep in energy to interact with other atomic orbitals.

Fluorine 2s overlap

This molecular orbital does not involve the atomic orbitals of the carbon atoms. Instead, it is the overlapping of the 2s orbitals of 2 fluorine atoms and is similar for the other 2 fluorine atoms but with different phases.

Fluorine 2P overlap 'hugging' This molecular orbital, like the previous one, does not involve orbitals from the carbon itself. In this molecular orbital, all the 2p orbitals are aligned and such that the one whole side of the molecule is the opposite phase of the other side. The result shows the 2 opposite-phased molecular orbital seemingly hugging each other.

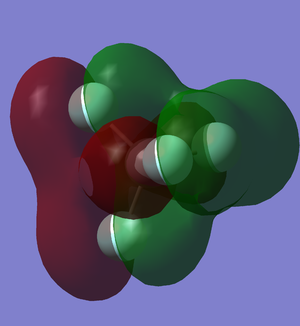
LUMO of CF4

After the carbon atoms form 4 bond with the fluorine atoms, the carbon's 2s and 2p orbital are used and occupied.

NH3