Rep:Mod:jv314
Computational Analysis of Cycloaddition Reactions: Transition States, Reactivity and Activation Energy Barriers
Introduction
Diels-Alder reactions, and cycloaddition reactions in general, are essential part of organic synthesis as they provide efficient route leading to wide scope of cyclic compounds. The mechanism of these reactions is in most cases concerted, i.e. the reaction from reactants to products happens in a single step and goes through single transition state - no intermediates are formed during the course of the reaction.[1] The concerted nature of these reactions makes the computational analysis of cycloadditions significantly simpler and faster since only one transition state structure and one corresponding activation energy barrier (AEB) need to be found. In order to calculate the AEB and in order to be able to evaluate the reactivity and thermodynamics in a given cycloaddition reaction, the energy-minimum structure of the reactants/products and the structure of the transition state (TS) need to be found.
On the potential energy surface, both minimum and transition state are stationary points, i.e. points where gradient is zero - infinitesimally small distortion from the structure results in zero change of energy. The difference between these two points lies in the curvature at these points. For a minimum, the curvature (second derivative) is always positive - small distortion in any direction will result in a trajectory leading back to this minimum. In the case of transition state, the curvature is negative in at least one direction - on 2D potential surface as in Figure 1 the TS is a saddle point for which the curvature in direction A is negative and displacement in this direction results in reaction trajectory away from the transition state (but in direction B the curvature is positive and trajectory could lead back to the transition state; thus it is essential to check the curvature with regard to more than one direction, i.e. to calculate more than one partial second derivative). Structure can be identified as a transition state if it has exactly one imaginary (negative) vibrational frequency - this frequency corresponds to the progress along the reaction coordinate from reactants to products through this transition state.
In this computational exercise, we use Gaussian 09W to first examine simplest Diels-Alder reaction of butadiene with ethene (Exercise 1). Later, more complex Diels-Alder reactions of benzoquinone with cyclopentadiene and of o-xylylene with sulfur dioxide are examined in Exercises 2 and 3, respectively. Finally in Further Work, the methods used in these exercises are used to analyze reactivity in yet-unpublished 1,3-dipolar cycloaddition reactions of nitrilimine with terminal alkenes. The activation energy barriers are computed for the [3+2] formation of 1,3,5- and 1,3,4-trisubtituted pyrazolines and for the [1+2] formation of cyclopropane. The computationally obtained results are then compared with the empirically observed data.
Nf710 (talk) 09:53, 21 November 2016 (UTC) Very good introduction. Excellent understanding of the basic principles. It would have been good if you could have put some understanding of the various levels of theory.
Exercise 1: Reaction of Butadiene with Ethene
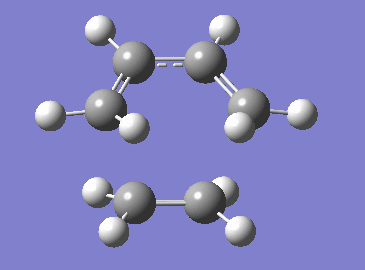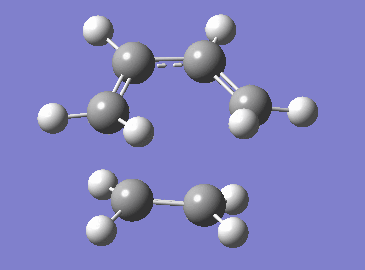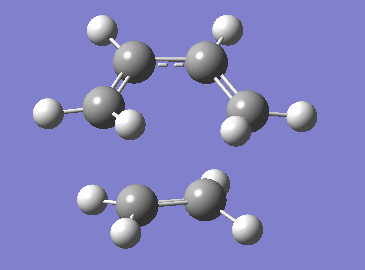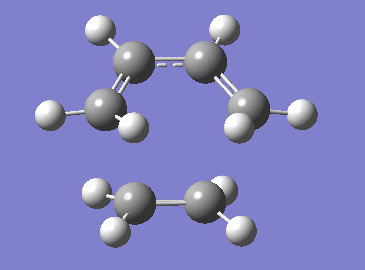
The reaction of butadiene with ethene is simple example of Diels-Alder reactions and a good starting point for computational analysis of these reactions. The reaction proceeds in a concerted manner through a transition state shown in Figure 2.[2] In this exercise, the orbital interaction in the transition state and the synchronicity/asynchronicity of this concerted reaction are examined. Both butadiene and ethene are electron-neutral as they lack any electron-donating or electron-withdrawing groups. This electron-neutrality causes a large energy gap between Frontier MOs of the correct symmetry in these reactants (as shown in Figure 3) which results in poor interactions of these orbitals and thus in poor overall reactivity. Therefore, dienes and dienophiles used in Diels-Alder reactions often have substituents which decrease the energy gap between MOs of the same energy thus improving the orbital interactions and reactivity - more on this in Exercise 2.[1]
Orbital Interaction
The Frontier MOs in Figure 3 are assigned symmetry labels g (gerade - antisymmetrical) and u (ungerade - symmetrical) based on their symmetry with respect to the plane of symmetry perpendicular to both the plane of these molecules and the bond between the middle carbons and going through the centre of these carbon bonds. The orbitals that contribute to the formation of the TS and consequently the resulting cyclohexene are the HOMOs and LUMOs of the reactants - their computed representation shown in Figures 5 and 6. These 4 MOs combine and form 4 new MOs in the transition state - these are the HOMO-1, HOMO, LUMO and LUMO+1 shown in Figure 4.[2] Using the MO symmetry, it is clear from which MOs of the reactants were the MOs in the TS formed. The TS HOMO and LUMO are result of ungerade-ungerade interaction of butadiene LUMO and ethene HOMO (Figure 5). The TS HOMO-1 and LUMO+1 are result of gerade-gerade interaction of butadiene HOMO and ethene LUMO (Figure 6). These g-g and u-u interactions have non-zero overlap integral and are allowed. Conversely, the gerade-ungerade interactions have zero overlap integral and are disallowed. It can be concluded that for the reaction to be allowed the HOMO of one of the reactants and the LUMO of the other must have the same symmetry.
Mechanism
Transition state in the examined reaction was found using the Semi-Empirical PM6 method. The conducted computational analysis allowed us to confirm the concerted fashion of the chosen Diels-Alder reaction and also to evaluate the synchronicity/asynchronicity of this cycloaddition. The correctness of the found TS structure was confirmed by the vibrational frequency analysis. Exactly one negative frequency corresponding to the formation of the new C-C bonds was found for the TS structure (Figure 7) - the remaining frequencies were all positive with the lowest one being the rotation of the ethene fragment out of the plane of the newly forming C-C bonds (Figure 8). The change of energy along the reaction coordinate (Figure 9) obtained from the IRC calculation illustrates the concerted fashion of examined reaction - distortion of the obtained transition state lead in one direction to the product and in opposite direction back to the reactants (which are higher in energy than the product).
The change in length of the C-C bond as the reaction progresses is shown in Table 1. In reactants, bonds C1-C2, C3-C4 and C5-C6 are C-C double bonds with lengths around 1.33 Å typical for sp2 hybridized carbon-carbon bonds.[3] As the reaction progresses from reactants through the TS towards the product, these bonds start to lengthen until they reach the typical sp3 hybridized C-C bond length of approximately 1.53 Å in the product.[3] The inverse and expected behavior is observed for the C2-C3 bond which goes from a slightly shorter (because of the conjugation between the two C-C double bonds)[2] C-C single bond in the reactants to a typical C-C double bonds in the products. The newly forming sigma bonds C4-C5 and C6-C1 are significantly longer in the TS structure than a typical C-C sigma bond but are still close enough for an interaction between the correct FMOs to happen (2.11 Å which is less the 1.5x of the Van der Waals atomic radius of carbon 1.70 Å - indicating short enough interatomic distance for orbital interactions to occur).[4]
Further, based on the obtained data, it can be concluded that the examined reaction proceeds in highly synchronous manner as both newly forming C4-C5 and C6-C1 have the same length and also the lengthening C1-C2 and C3-C4 bonds have the same length in the TS structure. This synchronicity is also apparent from the negative frequency animation for the TS in Figure 7.
 |
 |
 |
|
 |
 |
 | |||||||||||||||||||||||||||||||||
Nf710 (talk) 10:09, 21 November 2016 (UTC) Section very well done
Exercise 2: Reaction of Benzoquinone with Cyclopentadiene
The Diels-Alder reaction of benzoquinone with cyclopentadiene is examined as a more complex alternative to reaction in Exercise 1. With the dienophile being benzoquinone, two possible geometries of the transition state are now possible - compared to to the simple example with ethene where only one geometry was possible. The possible reactant approach trajectories and geometries of the TS are the exo and endo as shown in Figure 10. With a different approach trajectory, there arises a difference between the exo and endo in the secondary orbital interactions resulting in different activation energy barriers for the exo and endo TSs.[1] However, we should first examine the primary orbital interactions in our TSs.
Orbital interactions
In the Exercise 1, we examined a Diels-Alder reaction of electron neutral substrates - which meant that interaction between diene HOMO and dienophile LUMO was roughly as favorable as interaction between diene LUMO and dienophile HOMO as the energy gap within these orbital pairs was very similar. In case of benzoquinone, the presence of electron-withdrawing groups (carbonyl) moves both of the HOMO and LUMO lower in energy. The presence of sp3 hybridized carbon (which is slightly electron-donating) attached to the reacting termini of the diene results in destabilisation of the diene HOMO and LUMO and their increase in energy.[1] Both these factors combined result in considerably smaller energy gap (compare with Figure 3) between the diene HOMO and dienophile LUMO and interaction between these two orbitals is then the main MO interaction in the transition state as shown in Figure 11. The combination of electron-rich diene and electron-deficient dienophile as in this case is an example of a normal electron-demand Diels-Alder reaction.[1] The LUMOs in the TSs of both exo and endo paths correspond to the diene HOMO/dienophile LUMO antibonding orbital combination (shown in Figures 12 and 13) as expected. However, the HOMOs for the transition states (Figures 14 and 15) resemble more the combination of the diene HOMO with the dienophile HOMO (interaction of two occupied orbitals) which is not expected based on Figure 11 - it is possibly a result of more complex orbital interactions that cannot be predicted based on the simple MO diagram in Figure 11. Orbital that would closely resemble the bonding diene HOMO/dienophile LUMO orbital combination could not be found which further supports the presence of more complex orbital interaction in the transition states.
Nf710 (talk) 10:24, 21 November 2016 (UTC) this is due to mixing of higher states and because B3LYP has its exchange correlation slightly parameterised
 |
 |
 |
 |
 |
For the endo TS, secondary orbital interaction take place and since they are bonding in nature they result in stabilization of the endo TS compared to the exo TS. Observed secondary orbital interactions are through space interactions between the MOs on the middle carbons of the diene and the MOs on dienophile opposite to the reacting C-C double bond - visible in the Jmol file below.
The HOMO of the endo TS |
Additionally, the analysis of the lengths of the newly forming carbon-carbon bonds reveals that this reaction is synchronous (as for reaction in Exercise 1) - the formation of both bonds progresses simultaneously at the same rate.
Nf710 (talk) 10:25, 21 November 2016 (UTC) Very nice model of the secondary orbital interactions
Thermochemistry
By running frequency calculations for reactants, TSs and products, thermochemistry data were obtained for these structures (Table 2). By comparing the sum of the energies of the reactants at infinite separation with the energy of the respective TS, the values of activation energy barrier for both reaction proceeding through exo and endo TSs were found. The activation energy barrier for the endo path was found to be lower which agrees with our prediction based on the stabilizing effect of the secondary orbital interactions. The endo product is therefore the kinetic product. Using the DFT B3LYP-31(d) method both endo and exo products were found to be close in energy with the endo product being slightly lower in energy making it also the thermodynamic product. The obtained data suggest that both exo and endo reaction paths are endothermic as the calculated reaction energies are positive (products are higher in energy than reactants). This, however, does not agree neither with empirical data nor with more accurate computational data published for this exact reaction. The problem lies in the energies obtained for the products which are lower than they are supposed to be - both activation energy and reaction energy are more positive than they should be.[1][5] Despite this obstacle, the trend resulting from the obtained data is similar to the real reactivity.
| Energy (Hartree/particle) | kJ/mol | ||||||
|---|---|---|---|---|---|---|---|
| Cyclopentadiene | Benzoquinone | Sum for products | Transition state | Product | Activation energy | Reaction energy | |
| Endo DA | -194.034782 | -381.396831 | -575.431613 | -575.383844 | -575.427062 | 125.393625 | 11.94637 |
| Exo DA | -575.381326 | -575.426758 | 132.003375 | 12.74438 | |||
Nf710 (talk) 10:31, 21 November 2016 (UTC) Excellent argument and use of references to back up the argument. Your energies are correct because you used infinite seperation. However it would be typically more accurate to take the first and last geometries of the IRC so there isn't a seperation energy. This section is very well done.
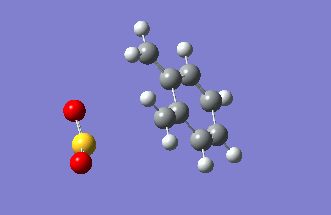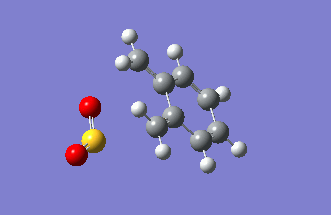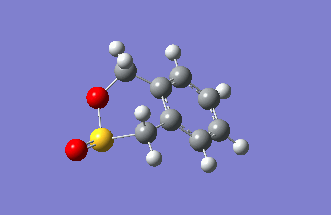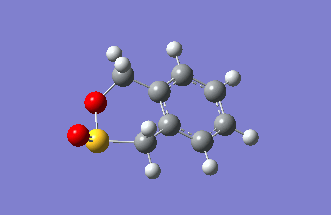
Exercise 3: Diels-Alder vs Cheletropic
In previous exercise we examined Diels-Alder reactions leading to formation of 6-membered carbon rings. In this exercise we examine the Diels-Alder reaction of sulfur dioxide with o-xylylene (Figure 16) leading to formation of 6-membered heterocycle - exo and endo TS as in Exercise 2 possible. The competing cheletropic reaction on sulfur is also examined (Figure 17). Further, in xylylene there are present two cis-butadiene fragments one terminal (DA reaction at this site shown in Figure 16) and an internal one (endo DA reaction at this site shown in Figure 18). The endo DA reaction at the internal cis-butadiene fragment is compared to the addition at the terminal fragment. In all four cases the vibrational frequency analysis using semi-empirical PM6 method confirmed the correctness of the TSs structures (exactly one negative frequency in each case corresponding to the reaction trajectory). The progress of the reactions from reactants towards the products is shown in Figures 20-23 - obtained from the IRC calculations. All 4 examined reactions of o-xylylene with sulfur dioxide are slightly asynchronous. In the Diels-Alder reactions formation of carbon-oxygen bond progresses slightly faster than formation of the carbon-sulfur bond. In the cheletropic reaction formation of one of the carbon-sulfur bonds progresses slightly faster. This asynchronicity is, however, quite weak in comparison to reactions examined in Further Work.
In addition to the frequency calculations for the TSs, frequency calculations were also run for the reactants at infinite separation and products (only positive frequencies present as expected) obtaining the thermochemistry data as in Exercise 2. These data were used to calculate the activation energy barriers and the reaction energies (Table 3). The endo DA reaction at the terminal cis-butadiene fragment was found to have the lowest activation energy barrier and the resulting product is therefore the kinetic product of reaction between o-xylylene and sulfur dioxide. The exo DA reaction at the terminal cis-butadiene fragment has slightly higher activation energy but the resulting product is slightly more thermodynamically stable. The cheletropic reaction has considerably higher activation energy barrier but the product is significantly more stable than products of other compared reactions which makes the cheletropic product the thermodynamic product of the reaction between o-xylylene and sulfur dioxide - the remaining presence of two strong sulfur-oxygen double bonds possibly stabilizes this product. Endo DA reaction at the internal cis-butadiene fragment has the highest activation energy barrier and it also is endothermic with its product being less thermodynamically stable than the reactants at infinite separation. Other three reactions are exothermic - significant stabilization of the products is the result of aromatization of the 6-membered carbon ring forming a benzene ring with significant stabilization due to the delocalization of the pi-electrons (aromatization visible in Figures 20-22). Product of reaction in Figure 18 is not aromatic and therefore it is much higher in energy. The reaction profile of the 4 examined reactions is included in Figure 19 for better visualization of the thermochemistry data.
(Good paragraphs Tam10 (talk) 18:16, 8 November 2016 (UTC))
| Energy (Hartree/particle) | kJ/mol | ||||||
|---|---|---|---|---|---|---|---|
| o-Xylylene | Sulfur dioxide | Sum for products | Transition state | Product | Activation energy | Reaction energy | |
| Endo DA at terminal cis-butadiene | 0.178376 | -0.118614 | 0.059762 | 0.090562 | 0.021701 | 80.850000 | -99.910125 |
| Exo DA at terminal cis-butadiene | 0.092078 | 0.021455 | 84.829500 | -100.555875 | |||
| Cheletropic reaction | 0.099059 | -0.000001 | 103.154625 | -156.877875 | |||
| Endo DA at internal cis-butadiene | 0.10207 | 0.06561 | 111.058500 | 15.351000 | |||
(Note that summing reactants in this way will not include any interaction energies! Tam10 (talk) 18:16, 8 November 2016 (UTC))
 |
 |
 |
 |
 |
 |
 |
 |
Further Work: Nitrilimine Cycloadditions to Terminal Alkenes
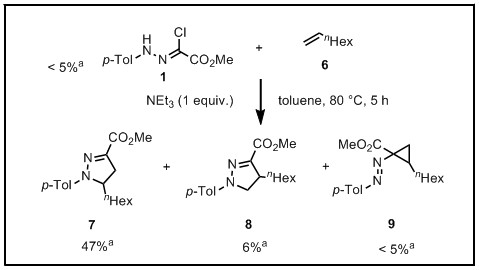
During summer 2016 I conducted a UROP project on use of Deep Eutectic Solvents (DESs) in 1,3-dipolar nitrilimine cycloadditions. Conversions in these solvents were compared with conversions in toluene - solvent commonly used in nitrilimine cycloadditions.[6] The nitrilimine dipole 
was prepared in situ from corresponding hydrazonoyl chloride by base-facilitated dehydrochlorination. One nitrilimine (Figure 24) was tested against three different terminal alkenes (reacting as dipolarophiles) of different electronic properties - butenone (electron-deficient), styrene (electron-neutral) and 1-octene (electron-rich). The cycloaddition of used nitrilimine was reported to work best with electron-deficient dipolarophile[7] which agrees with the obtained experimental data (Figures 25-27). Poorer reactivity was observed for styrene compared to butenone. The reactivity of 1-octene was much worse and required both higher temperatures and longer reaction times. With butenone and styrene, only formation of 1,3,5-trisubstituted pyrazoline as shown in Figures 25 and 26 was observed. With 1-octene as dipolarophile, in addition to 1,3,5-trisubstituted pyrazoline the formation of 1,3,4-trisubstituted pyrazoline and cyclopropane byproduct (result of [1+2] cycloaddition) was also observed. In this computational analysis the structures of reactants and transition states are optimized using the DFT B3LYP-31(d) method, and activation energy barriers are calculated and compared for the possible cycloaddition reactions. Even though better conversions were achieved with DESs as reaction media, calculations are conducted using CPCM solvation model with toluene as solvent since DESs are a novel class of solvents that only recently came into field of interest of computational chemistry and further research is required.[8]
 |
 |
 |
a 1H NMR conversions are the average of at least two independent experiments and determined with respect to 1,3,5-trimethoxybenzene as internal standard
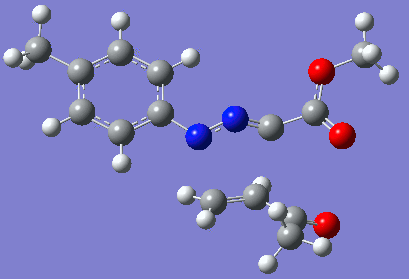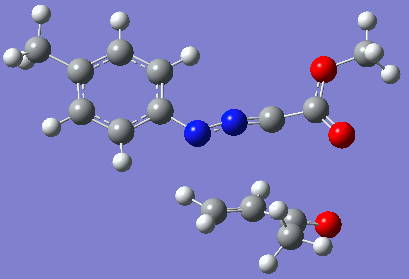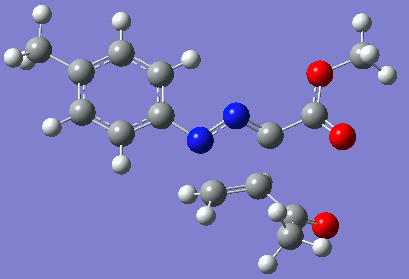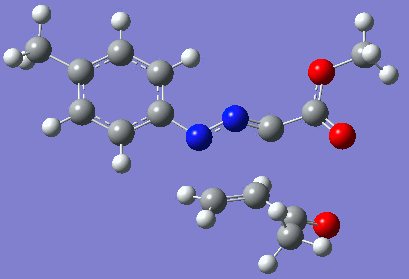
Reaction with butenone leading to 1,3,5-trisubstituted pyrazoline (Figure 25) was examined first since butenone has the smallest number of atoms. The TSs in endo (Figure 28) and exo (Figure 29) reactions with butenone were examined and a smaller activation energy barrier was found for the exo TS (Table 4). Based on this result, the computational approach was approximated and only exo TSs were examined for remaining reactions. The formations of 1,3,5-trisubstituted pyrazolines and 1,3,4-trisubstituted pyrazolines were examined for all 3 substrated (Figures 29-34). The 1,3,5-trisubstituted pyrazolines were found to have lower activation energies in all 3 cases which agrees with empirical data. The trend of activation energy - lowest for butenone and highest for 1-octene - also agrees with empirical data. With 1-octene, the formation of cyclopropane as shown in Figure 27 was also examined. For this reaction, highest activation energy barrier was calculated. The correctness of all TS structures was confirmed by vibrational frequency analysis - exactly one negative frequency present for each TS (visualisations in Figures 28-35). Difference in activation energy between 1,3,5 and 1,3,4 is smallest for 1-octene which could partially explain why is the 1,3,4 isomer observed with this alkene but not with the others.
Lengths of the newly forming bonds in the TS structures were measured (Table 5). The 1,3,5 reaction path was found highly asynchronous with C-C bond forming prior to C-N bond. The 1,3,4 reaction is more synchronous and increase in synchronicity is observed for more electron-deficient alkenes (with butenone C-C and C-N bonds in TS have closely similar lengths). The cyclopopane formation was found to be strongly asynchronous with the C-C bond first forming to the terminal carbon of 1-octene. These data are in agreement with literature.[9]
(Any idea for why there are these trends? How do electron-withdrawing and electron-releasing groups affect the barrier? In terms of isomers between 1,3,4 and 1,3,5, why would the orientation affect the barrier? Is it a steric or electronic effect? If you want to go further and write about this, it would be worth talking about these points Tam10 (talk) 18:16, 8 November 2016 (UTC))
 |
 |
 |
 |
 |
 |
 |
 |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
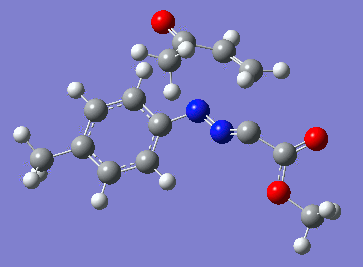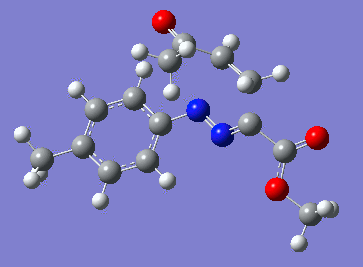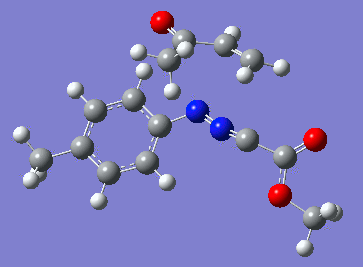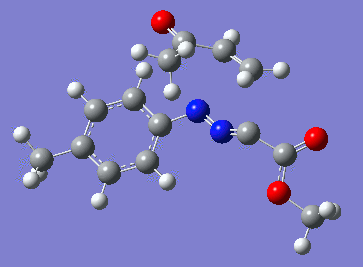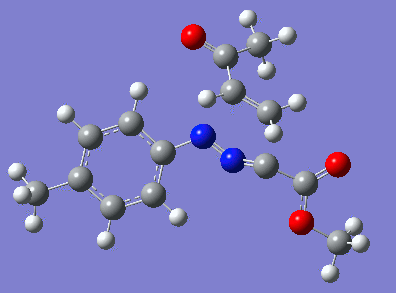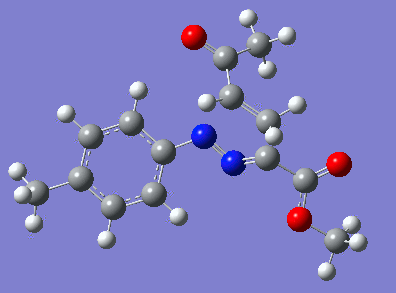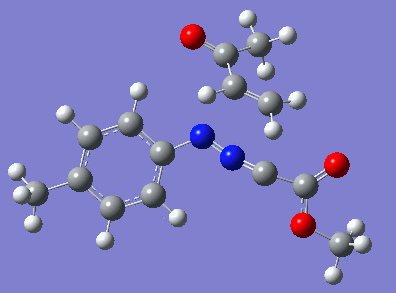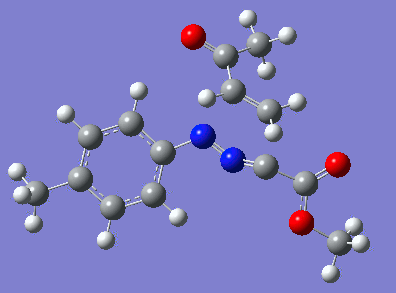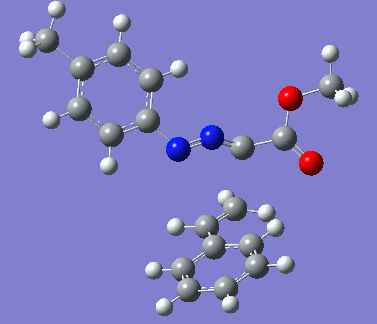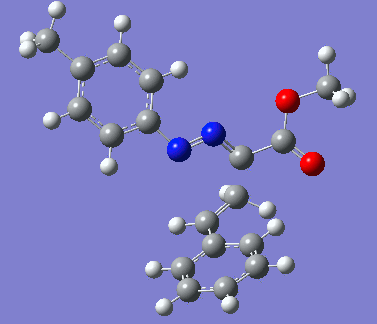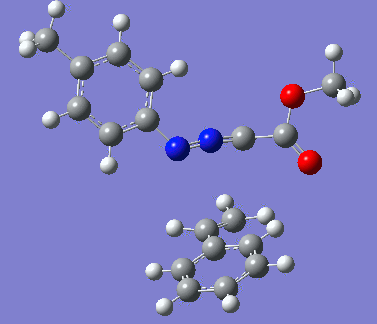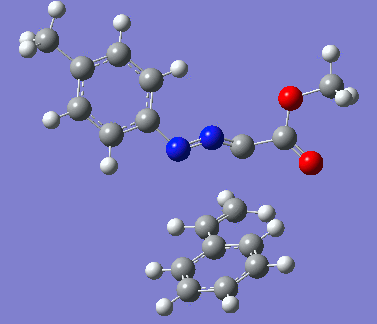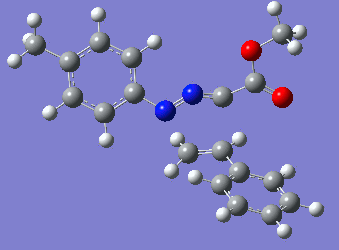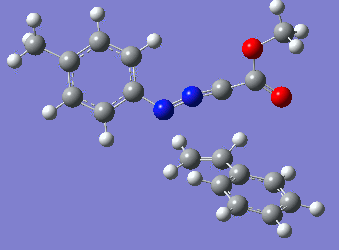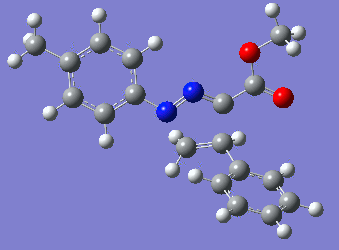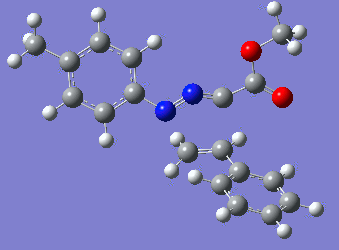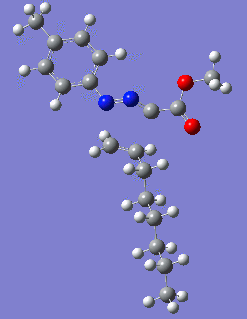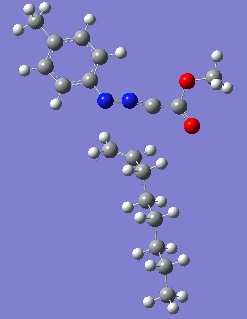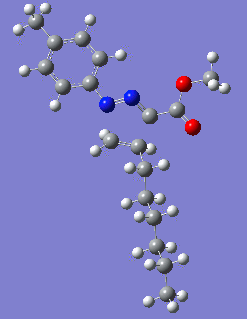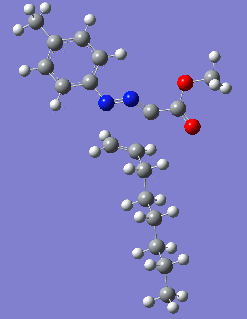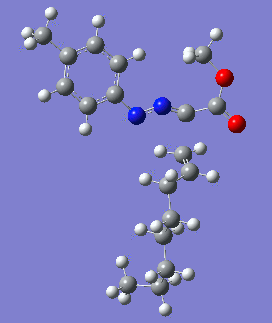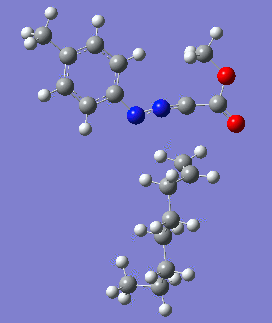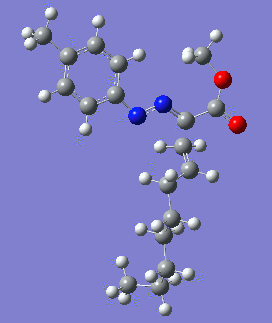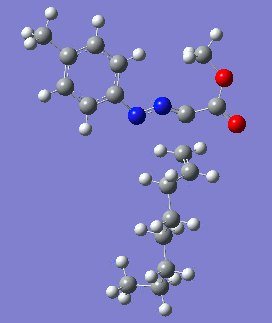(Easy to read tabulated data here Tam10 (talk) 18:16, 8 November 2016 (UTC))
(+22% Tam10 (talk) 18:16, 8 November 2016 (UTC))
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Nicolaou, K. C., Snyder, S. A., Montagnon, T., & Vassilikogiannakis, G. (2002). The Diels-Alder reaction in total synthesis. Angewandte Chemie - International Edition, 41(10), 1668–1698.
- ↑ 2.0 2.1 2.2 Houk, K. N., Lin, Y. T., & Brown, F. K. (1986). Evidence for the concerted mechanism of the Diels-Alder reaction of butadiene with ethylene. J. Am. Chem. Soc., 108(3), 554–556.
- ↑ 3.0 3.1 Brockway, L., & Pauling, L. (1937). Carbon-Carbon Bond Distances. The Electron Diffraction Investigation. Journal of the American Chemical Society, 59(7), 1223–1236.
- ↑ Batsanov, S. S. (2001). Van der Waals Radii of Elements. Inorganic Materials Translated from Neorganicheskie Materialy Original Russian Text, 37(9), 871–885.
- ↑ Tormena, C. F., Lacerda, V., & De Oliveg, K. T. (2010). Revisiting the stability of endo/exo diels-alder adducts between cyclopentadiene and 1,4-benzoquinone. Journal of the Brazilian Chemical Society, 21(1), 112–118.
- ↑ L. De Benassuti, L. Garanti and G. Molteni, Tetrahedron, 2004, 60, 4627–4633.
- ↑ G. Molteni, A. Ponti and M. Orlandi, New J. Chem., 2002, 26, 1340–1345.
- ↑ Ashworth, C. R., Matthews, R. P., Welton, T., & Hunt, P. A. (2016). Doubly ionic hydrogen bond interactions within the choline chloride-urea deep eutectic solvent. Physical Chemistry Chemical Physics, 18(27), 18145–18160.
- ↑ Mawhinney, R. C., Muchall, H. M., & Peslherbe, G. H. (2005). A computational study of the 1,3-dipolar cycloaddition reaction mechanism for nitrilimines. Canadian Journal of Chemistry, 83(9), 1615–1625.