Rep:Mod:jt2010Mod3
Module 3
Optimizing the Reactants and Products
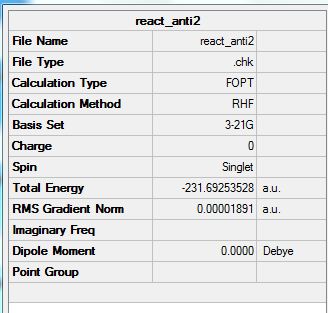
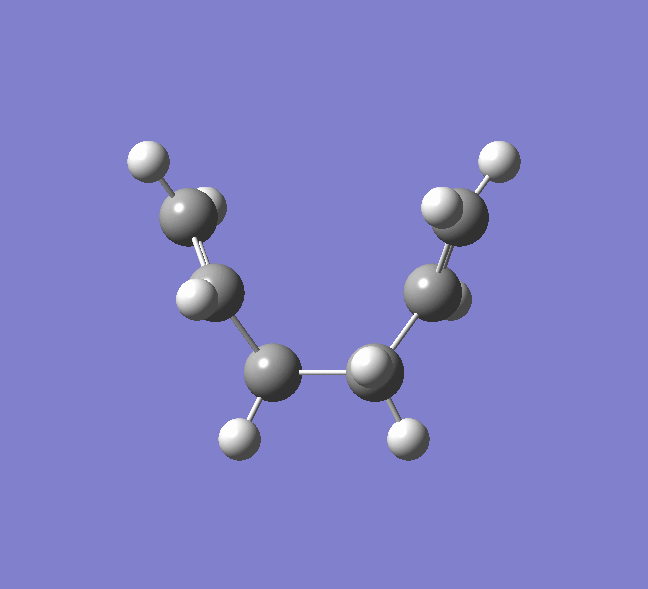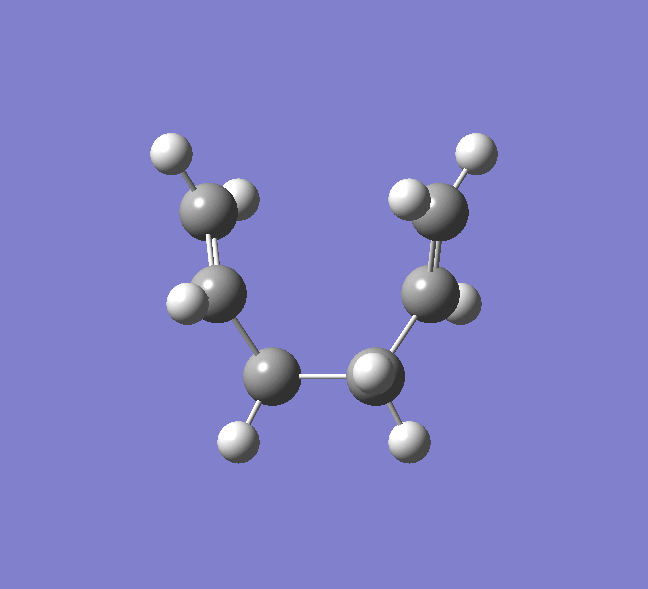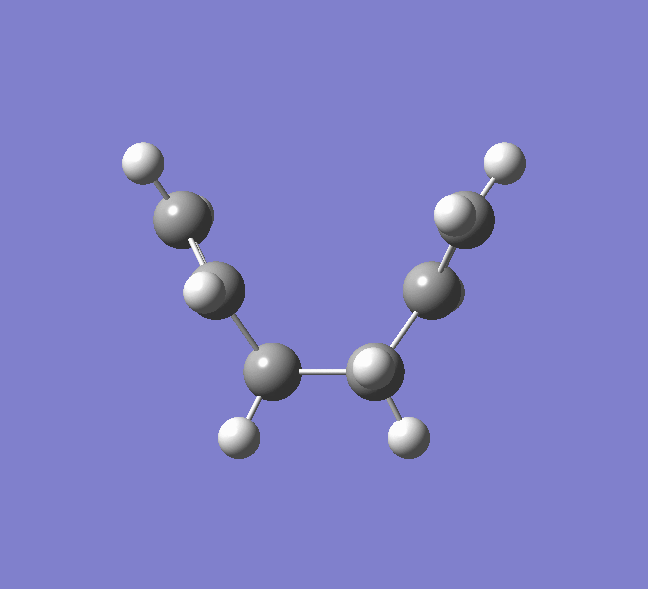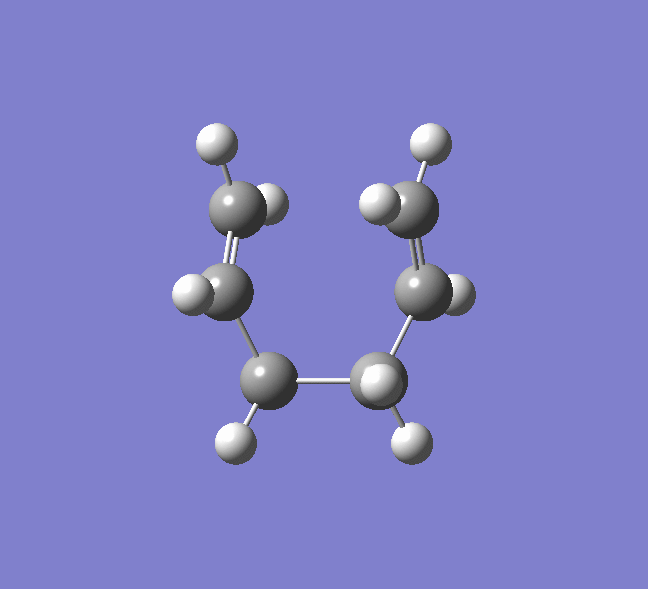
Antiperiplanar Arrangement:
Summary:
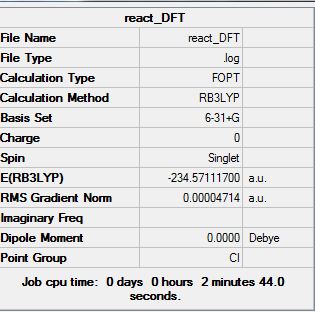
The final structure does show some symmetry as there is a line of symmetry across the xy plane. This is so that the atoms can have the least steric hindrance possible. The symmetry labels recorded are Ci.
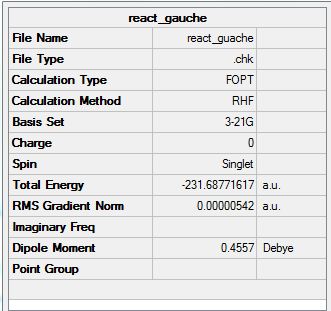
Gauche Conformation:
Summary:
The symmetry shown is C1.
Activation energies and Enthalpies
Calculated activation energies and enthalpies use the lowest energy conformation of a reactant molecule as a reference. As such it will be conformation which has the least steric repulsions and the most stabilizing orbital interactions. From the energies calculated above for app and gauche, it can be seen that app, is going to be lowest energy conformer.
Compare structures in Appendix 1 with optimized structures
From the APP optimization which gives the energy as -231.69253528 a.u this compares very well with the anti2 conformation given in appendix 1. The value given in appendix 1 is -231.69254 a.u. As such the low energy conformer of 1,5-hexadiene is Ci.
For the gauche conformation, the energy given is -231.68771617 a.u. This compares to the gauche 1 conformer in appendix 1. The value given in appendix one is -231.68772 a.u. As such this low energy conformer of 1,5-hexadiene is C2.
The energy comparison between the optimized Ci molecule (-231.69253528 a.u) and the one shown in appendix 1 (-231.69254 a.u.) is 4.72x10-6 a.u. This is relatively small compared to the size of the energies and as such shows us that the final energies calculated using optimization are very close to the true value.
Optimized using B3LYP/6-31G*
Summary:
As can be seen from the summary table, the total energy is much less using this method for calculation. Using the HF/3-21G the energy is: -231.69253528 a.u Using DFT/6-31G*, the energy is: -234.57111700 a.u
From this we can see that there is a 2.87858172 a.u difference which is huge. Although these figures can not be compared directly, it shows that the higher level of theory calculation has found the lower energy conformer.
As can be seen from the summary the symmetry is given as Ci without the need for us to manually ask the program to give it a symmetry label for us. As such, there is a change in overall geometry, however this is not very big.
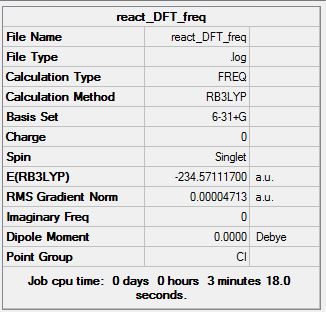
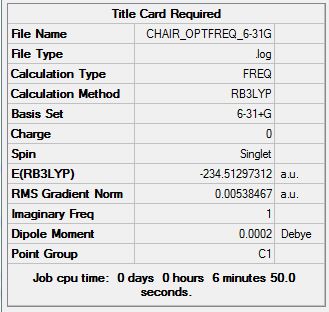
Frequency Calculation
Sum of electronic and zero-point Energies= -234.428083 Sum of electronic and thermal Energies= -234.420769 Sum of electronic and thermal Enthalpies= -234.419825 Sum of electronic and thermal Free Energies= -234.459745
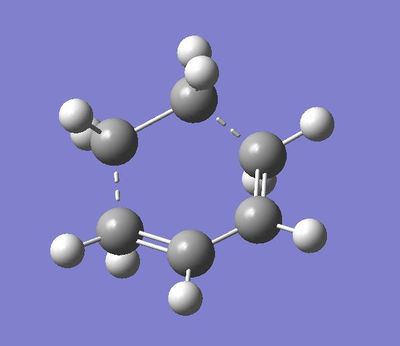
Optimizing the 'Chair' Transition Structures
Optimized allyl fragment
Summary:
test molecule |
The Chair guess can be found here:
File:Chair ts guess.gjf
This is the file where the 2 optimized CH2CHCH2 molecules are ~2.2 Armstrongs apart.
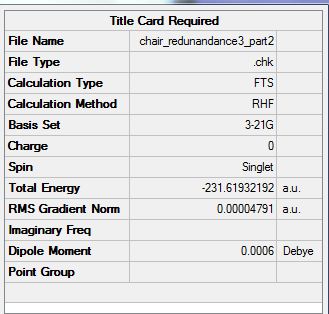
The optimized chair using method: opt+freq and Optimization to a TS (Berny)
The optimized structure has a frequency of magnitude ~818cm-1 shown here:
test molecule |
The optimized molecule has terminal C-C bond breaking/forming bonds at average: 2.020355 Angstroms.
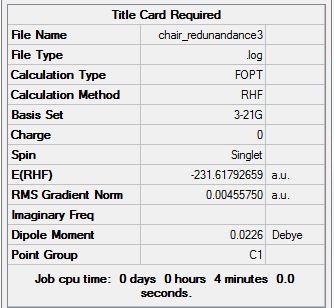
The optimized chair using method: Optimization with Redundant Coord Editor and co-ordinates frozen.
In the above method, the optimized structure looks similar to the transition optimized using the TS (Berny). However the bond forming/breaking distances were fixed to ~2.2 Armstrongs. Average terminal C-C bond distance is 2.156475 Angstroms. However these can now be optimized to give:
This is done by changing the terminal C-C bond atoms to have a derivative setting during optimization.
File:CHAIR REDUNANDANCE3 PART2.LOG
The Average terminal carbon bond separation is: 2.02058 angstroms.
Comparison
| TS (Berny) Optimization | Frozen Cooord Optimization | ||
|---|---|---|---|
| Terminal C-C separation (angstroms) | 2.020355 | 2.02058 | |
| Total Energy (a.u) | -231.61932247 | -231.61932192 |
From the structure we can see the big difference is that in the TS(Berny)Optimization there are 4 bonds observed which are each of a 1.5 bond order. However in the Frozen Coord Optimization there is 2 double bonds and 2 single bonds. What this means is the electron density has been concentrated to one side of the molecule and it is at this side of the molecule that the terminal C-C bonds are likely to form first.
However if we look at the C-C separation, for both methods, the separation does not change very much. What this implies is that both models have taken into account factors such as orbital overlaps and steric hindrances, to get the optimized bond lengths.
The energies differ only at the 6th decimal point, and from this we can say that both are low energy conformers.
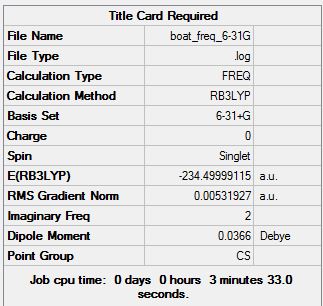
Optimizing the 'Boat' Transition Structures
Firstly labeling of the reactant and product atoms must be done:
Using the QST2 optimization method we get:
Summary:
As can be seen here, Guassian has failed as it did not rotate around the central bonds. As such the bonds have been elongated and are crossing which is unrealistic. If this is to work then the c-c-c-c of the reactant molecule the dihedral angle must be 0 degrees. The inside c-c-c must be reduced to 100 degrees shown below:
The optimized molecule shows this:
Summary:
The imaginary frequency is as follows:
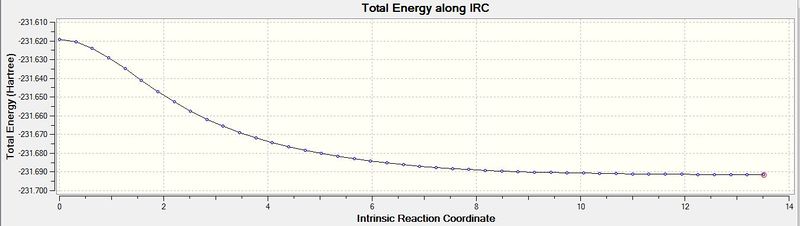
Iintrinsic Reaction Co-ordinate (IRC)
The IRC is the method which allows us to follow the minimum energy path from a transition structure down to its local minimum on a potential surface. I will now optimize the chair transition structure and using IRC with 50 points in the forward direction.
Lowest energy = -231.69157536 a.u
From the above information it can be seen that there this has given the formation of the bond, but more is needed, as the gradient is still not steady. ie. the calculation has not finished. As such to reach the minimum geometry I will recalculate the force constants after each point.
The lowest energy from the plot is: -231.69157878 a.u
This is true as from the plot we can see that the gradient evens out which means the minimum has been reached. Thus this is the lowest energy.
Calculate the activation energies
Chair frequency analysis at HF/3-21G
Sum of electronic and zero-point Energies= -231.466700 Sum of electronic and thermal Energies= -231.461341 Sum of electronic and thermal Enthalpies= -231.460397 Sum of electronic and thermal Free Energies= -231.495206
Boat frequency analysis at HF/3-21G
Sum of electronic and zero-point Energies= -231.450929 Sum of electronic and thermal Energies= -231.445300 Sum of electronic and thermal Enthalpies= -231.444356 Sum of electronic and thermal Free Energies= -231.479775
Chair conformer using B3LYP/6-31G*
Once symmetry has been done on it, it is C2h symmetry.
Sum of electronic and zero-point Energies= -234.369094 Sum of electronic and thermal Energies= -234.362667 Sum of electronic and thermal Enthalpies= -234.361723 Sum of electronic and thermal Free Energies= -234.398934
Boat Conformer optimised using B3LYP/6-31G*
Once symmetry has been performed, it gives C2v symmetry.
Sum of electronic and zero-point Energies= -234.356893 Sum of electronic and thermal Energies= -234.351048 Sum of electronic and thermal Enthalpies= -234.350104 Sum of electronic and thermal Free Energies= -234.385687
| HF, 3-21G | HF 3-21G | B3LYP/6-31G | EB3LYP/6-31G | ||
|---|---|---|---|---|---|
| Eelec + ZPE | Eelec +Etherm | Eelec + ZPE | Eelec +Etherm | ||
| Anti 2 a.u | -231.539539 | -231.532565 | -234.428083 | -234.420769 | |
| Chair TS a.u | -231.466700 | -231.461341 | -234.369094 | -234.362667 | |
| Eact a.u | 0.072839 | 0.071224 | 0.058989 | 0.058102 | |
| Eact Kcal-1 | 45.70712805 | 44.83614902 | 37.0161284 | 36.45952792 |
| HF, 3-21G | HF 3-21G | B3LYP/6-31G | EB3LYP/6-31G | ||
|---|---|---|---|---|---|
| Eelec + ZPE | Eelec +Etherm | Eelec + ZPE | Eelec +Etherm | ||
| Anti 2 a.u | -231.539539 | -231.532565 | -234.428083 | -234.420769 | |
| Chair TS a.u | -231.450929 | -231.445300 | -234.356893 | -234.351048 | |
| Eact a.u | 0.08861 | 0.087265 | 0.07119 | 0.069721 | |
| Eact Kcal-1 | 55.60357249 | 54.75957289 | 44.67236571 | 43.75055499 |
From the table we can see that generally the Chair conformer has lower activation energies than the Boat conformer. This is due to less steric repulsions and better orbital overlaps. The bond angles will be less strained in the chair conformation and as such will be lower in energy and require less activation energy than the boat. The instructions give, experimental values of 33.5 ± 0.5 kcal/mol for the chair and 44.7 ± 2.0 kcal/mol for the boat at 0K. For both the chair and the boat the answers are relatively close, and the trend is immediately obvious. As such Guassian is a good guide to the energy predictions. On top of that it can be seen that the method of B3LYP/6-31G is much better than HF/3-21G in both the chair and boat conformations.
Diels Alder Conformations
All optimizations in this section will be done using AM1 semi-empirical optimization.
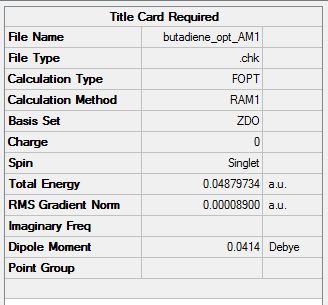
Cis Butadiene Optimize
CisButadiene was optimized using the AM1 method.
test molecule |
Summary:
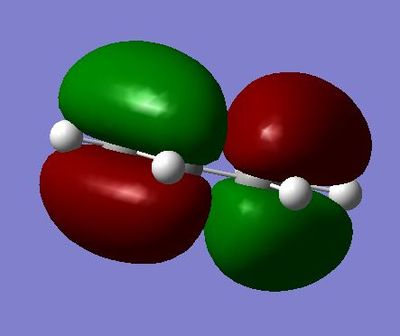
HOMO of the cis butadiene at energy: -0.34382 a.u and asymmetric
LUMO of the cis butadiene at energy: 0.01709 a.u and symmetric
Diene Transition Stat geometry
The computation of the Transition state geometry was done, which maximizes the overlap between the ethylene pi orbitals and the pi system on the butadiene.
Product optimized.
Log file: File:Log 65175.log
This has the HOMO at -0.39167 a.u and has a D2/ C1 symmetry.
The LUMO is at 0.13460
For the above calculations, an AM1 method was carried out with a guess bong length between ethene and butadiene as 1.8 angstroms. The molecule was drawn firstly from a bicyclo system and removing the CH2-CH2 fragment. The C-C bond lengths in the diels alder reaction have a bond length of 1.54766 angstroms.
Typical Sp3</sup C-C bondlengths are 1.54 Angstroms and Sp2 C=C bond lengths are 1.35520 angstroms. The van der Waals radius of a C atom is 1.7 angstroms. From this information we can say that the C-C bond in the TS is much shorter than the typical C-C bond. Also there will be steric hindrance as it exceeds the VDW radius.[1]
The Vibration which corresponds to the TS at -91.85 cm-1 is:
This is asynchronous as compares when compared to the lowest positive frequency: 224.76cm-1 we can see that the intensity of the IR is much bigger, which means it has a much bigger effect on the structure.
The HOMO at the transition structure is anti symmetric and uses the HOMO from ethene and the LUMO from cis butadiene. This is deduced from the fact that the HOMO of one reactant must react with the LUMO of another and from looking at the HOMO and LUMO complexes.
Study the regio-selectivity
Firstly we need to optimize the Cyclohexa-1,2-diene molecule.
Cyclohexa-1,2-diene
Summary:
Bond length of partly formed C-C bond: 1.48178 angstroms
The HOMO is -0.32074 and anti symmetric
The LUMO is 0.01692 and symmetric with respect to the plane
Symmetry is C2V
Then we need to optimize maleic anhydride.
Summary:
The HOMO is given at: -0.44187 and symmetric
The LUMO is given at: -0.05949 and asymmetric
ENDO Form
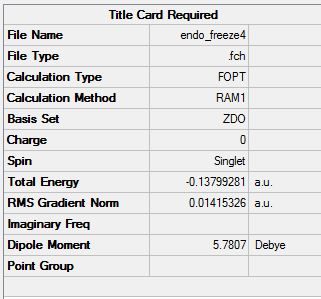
To form this, I will use the freeze method.
Summary:
The C-C bonds were then set to derivative.
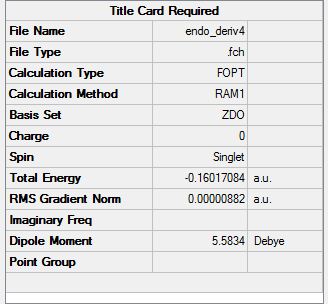
Summary:
The C-C bond lengths formed are: 1.53574 and 1.53576 respectively. Space distance between oxygen ad CH2-CH2 fragment: 1.53691
Space distance between oxygen ad CH2-CH2 fragment: 4.67325
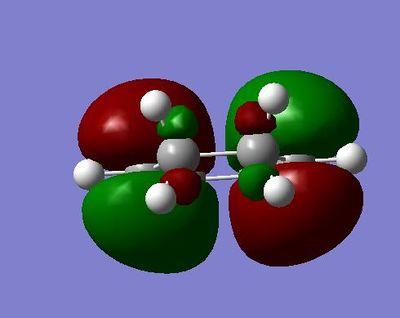
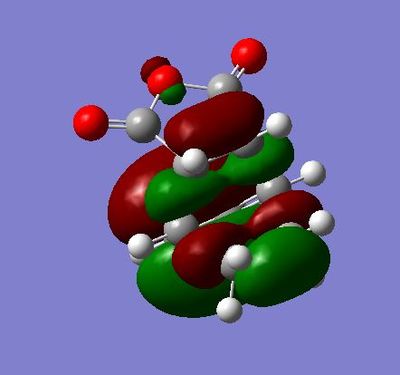
The HOMO is of energy -0.38708 and is symmetric relative to the plane
The LUMO is of energy 0.01077 and is asymmetric relative to the plane
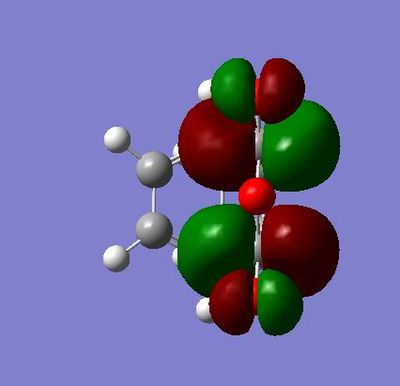
The HOMO here has a node on the central oxygen atom and no apparent electron density on the other oxygens.
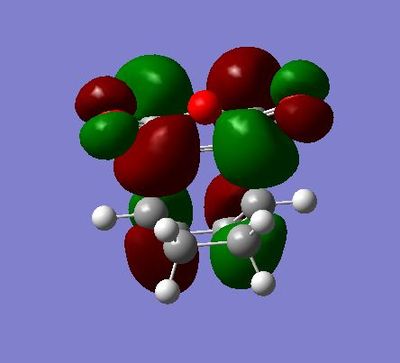
EXO Form
Summary:
The C-C bonds were then set to derivative.
Summary:
Partly Formed C-C Bond Lengths are: 1.53604 and 1.534603 respectively Other Bond Lengths are : 1.53510
Space distance between oxygen ad CH2-CH2 fragment: 3.06650
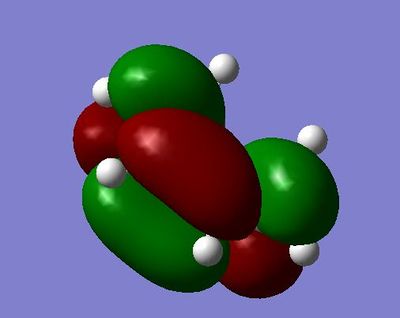
HOMO symmetric with respect to plane and of energy:-0.38787
LUMO asymmetric with respect to plane and of energy: 0.00602
In the HOMO, we can see that there a node on the atom and but there is bonding interactions along the top and bottom faces of the MO.
Compare the endo and exo and discussion
For the endo the energy is: -.160170084 a.u. For the exo the energy is: -0.15990937 a.u.
From this we can see that the exo is higher in energy than the endo. This is because the reaction is supposed to be kinetically controlled. As such because the endo will be the more likely adduct for this reaction. The higher energy can be said to be due to the steric repulsions between the steric repulsions of the CH2-CH2 and Maleic and hydride. For the the endo, slightly lower energy as the pi interactions between the CH2-CH2 and -(C=O)-O-(C=O)- fragments have a secondary orbital interaction.
[2] From this we can conclude that steric effects have a larger effect on the energy of the structure than secondary overlap effect.
References
- ↑ http://en.wikipedia.org/wiki/Van_der_Waals_radius
- ↑ Steric effects vs. secondary orbital overlap in Diels-Alder reactions. MNDO and AM1 studies, J. Org. Chem., 1987, 52 (8), pp 1469–1474