Week 1

Cyclopentadiene Dimer

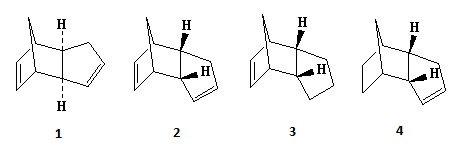
The dimerisation and hydrogenation^[1] of cyclopentadiene were investigated in this experiment. By looking at the characteristics of the dimers, one can predict the thermodynamics of the reaction. The diagram below shows the dimers under investigation. The results obtained through minimising the energy of the dimers using ChemBio3D Ultra (MM2 force field) are shown in the table below.

Parameter	Molecule 1 (exo dimer)	Molecule 2 (endo dimer)	Energy Difference	Molecule 3	Molecule 4	Energy Difference
Stretch	1.2859	1.2508	0.0351	1.2772	1.1301	0.1471
Bend	20.5800	20.8501	0.2701	19.8592	13.0150	6.8442
Stretch-Bend	-0.8382	-0.8355	0.0027	-0.8345	-0.5652	0.2693
Torsion	7.6557	9.5102	1.8545	10.8093	12.4113	1.602
Non-1,4 VDW	-1.4206	-1.5645	0.1439	-1.5627	-1.0520	0.5107
1,4 VDW	4.2323	4.3179	0.0856	5.6334	4.4405	1.1929
Dipole/Dipole	0.3775	0.4475	0.07	0.1621	0.1410	0.0211
Total energy	31.8765	33.9975	2.121	35.6850	29.2475	6.4375

The dimerisation of cyclopentadiene can result in two isomers, exo dimer (molecule 1) and endo dimer (molecule 2). The endo dimer is higher in energy by 2.121 kcal/mol compared to the exo dimer. The main contribution to the energy difference is torsion. The endo dimer has a larger torsion energy, difference of 1.8545 kcal/mol, compared to the exo dimer. Larger torsion energy of the exo dimer suggests that the groups have larger angles between them thus the isomer is more staggered (antiperiplanar) compared to the endo isomer. The more staggered conformer is favoured over the more eclipsed conformer as there is less steric repulsions between groups and it could lead to stabilisation by allowing sigma-sigma* overlap. Therefore the exo dimer is more thermodynamically stable and has a lower energy. Despite this, the endo dimer is the isomer that is formed during dimerisation of cyclopentadiene. This means that the reaction must be kinetically controlled, since the more thermodynamic stable product (exo-dimer) is not formed. Some might argue that the reason for this is due to secondary orbital interactions, with the endo isomer having additional stabilisation due to the interactions between occupied and unoccupied orbitals. This lowers the activation barrier of the endo isomer which has extra stabilisation energy that the exo isomer does not posse. However this does not fully account for the observed trend and the full explanation is far beyond the scope of the course ^[2].

The hydrogenation of cyclopentadiene could result in molecules 3 or 4. Molecule 4 has a lower energy, difference of 6.4375 kcal/mol, compared to molecule 3. The main contribution to their energy difference is the bending energy, with molecule 3 being higher by 6.8442 kcal/mol compared to molecule 4. In cyclopentadiene dimer, the double bonds in the 5-membered rings have unfavourable bond angles (ideally, 120 for sp2 atoms) which is the cause of this bending energy. Hydrogenation across the double bond can relieve the bending energy. The major (or only) product formed would be the hydrogenation of the more-strained double bond as this would lead to greater decrease in strain and energy of the molecule. One of the 5-membered rings consists of a bridge leading to another aromatic ring. The double bond in this ring has a higher strain compared to the other one so this is the double bond that is hydrogenated. This leads to molecule 4 with the lower bending and total energy and molecule 3 is only formed after prolonged hydrogenation.

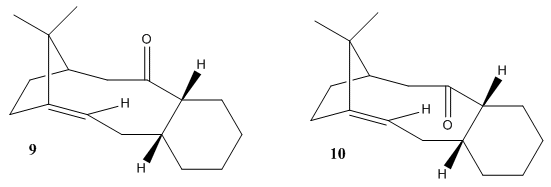
Atropisomerism in an Intermediate related to the Synthesis of Taxol

Atropisomers are formed when the rotation about single bonds is hindered and the steric strain barrier to rotation is high enough to allow for the isolation of the conformers. The Oxy-Cope rearrangement proposed by Paquette^[3] indicated intermediates which are atropisomers for Taxol synthesis. The intermediates are molecules 9 and 10 which differ by the direction of the carbonyl bond. The more stable intermediate can be found by performing calculations of energy minimisation with MM2 forcefield and results are shown in table below.

Parameter	Molecule 9 (up)	Molecule 10 (down)	Energy Difference
Stretch	3.2301	2.6209	0.6092
Bend	17.2721	11.3431	5.929
Stretch-Bend	0.2704	0.3433	0.0729
Torsion	18.2111	19.6657	1.4546
Non-1,4 VDW	0.3309	-2.1601	1.8292
1,4 VDW	13.8090	12.8724	0.9366
Dipole/Dipole	-1.6917	-2.0023	0.3106
Total energy (kcal mol^-1)	51.4318	42.6829	8.7489

MMFF94 force field can also be used which takes into account different interactions. The resulting energy is different to that of the MM2. However the same trend is observed, with molecule 10 being more stable than molecule 9.

Total Energy	Molecule 9	Molecule 10	Energy Difference
MM2	51.4318	42.6829	8.7489
MMFF94	76.2713	60.5581	15.7132

After performing both calculations, it can be seen that the “down” isomer is more stable, by 8.7489 kcal/mol (MM2) and 15.7132 kcal/mol (MMFF94), compared to the “up” isomer. The main contribution to the difference in energy is the bending energy, with “up” isomer being larger by 5.9290 kcal/mol compared to the “down” isomer. Therefore the “down” isomer is the thermodynamically more stable product and should be the major product under thermodynamic conditions. The six membered ring in both isomers can adopt different conformations and these are investigated. Twist boat conformations are less stable than the respective chair conformations and this can be seen by the increased in energy in the twist boat conformations (for both MM2 and MMFF94 force field) by comparing tables immediate above and below. It is worth mentioning that the 9a twist boat conformer is still higher in energy than the 10a twist boat conformer, further validating that carbonyl “up” is an unfavourable conformation. The relatively large energy difference between the chair and twist boat conformers suggests that it is difficult to twist the aromatic ring. The steric strain barrier to rotation is high enough to allow for the isolation of the conformers, forming atropisomers.

Total Energy	Molecule 9a	Molecule 10a	Energy Difference
MM2	57.4953	47.0648	10.4305
MMFF94	82.9969	66.7961	16.2008

Regioselective Addition of Dichlorocarbene to a diene

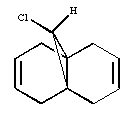
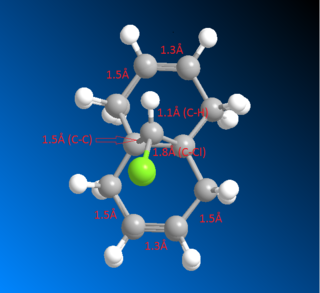
Overlay showing the bond distances of the molecule 12 above computed using MM2 DOI:10042/22251 and MOPAC DOI:10042/22250 :

After inspecting the the actual bond distances of the molecules minimised by MM2 and MOPAC, it can be shown that the bonds indicated below with 5Å have the largest differences between the two molecules (around 0.01Å). This suggests that the C-C bonds that are not shown in the diagram, ie C-C single bridging, C=C double and C-C single bond that connects the two aromatic ring together, are very fixed and non-flexible. Because MM2 and MOPAC takes into account different interactions in the molecule and both calculations yielded pretty much the exact same distance.

The vibrations of molecule 12 is also studied. The most important ones are outlined below.

Frequency	Intensity	Form of Vibration	Animation
770.86	25.1312	C-Cl stretch
1753.04	3.99363	C=C exo
1757.34	3.9363	C=C endo

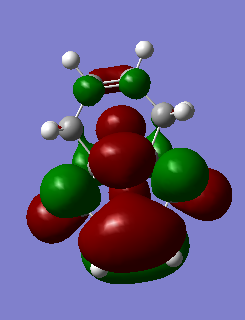
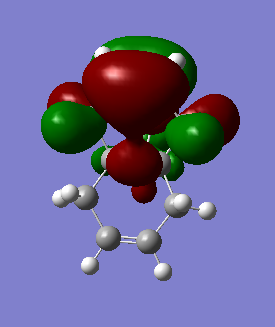
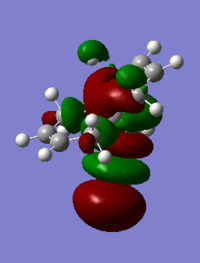
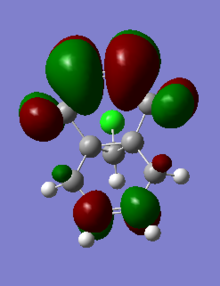
The table below shows the molecular orbitals of molecule 12^[4]. In HOMO-1, electron density can be seen in both double bonds, with the double bond that is exo to C-Cl having much larger lobes, i.e. it is more electron rich and more prone to nucleophilic attack. In HOMO however, the opposite is observed where larger lobes are seen on the double bond that is endo to C-Cl has and the other double bond has no electron density around it at all. This is the reason why carbenes attack the endo double bond instead of the exo double bond. In LUMO, the number of nodal planes has clearly increased and energy has changed from negative to positive, showing the increase in anti-bonding character. Orbitals are also smaller so they are less diffused. LUMO+1 has even more anti-bonding character in the MOs with higher energy and no electron density can be seen in the exo double bond. The trend continues to LUMO +2, where no large or diffused electron density can be seen and there is no electron density around the middle bridge and the Cl atom.

MO	Energy	MO picture
HOMO-1	-0.24519
HOMO	-0.23588
LUMO	0.01555
LUMO+1	0.02025
LUMO+2	0.03613

Monosaccharide chemistry and the mechanism of glycosidation

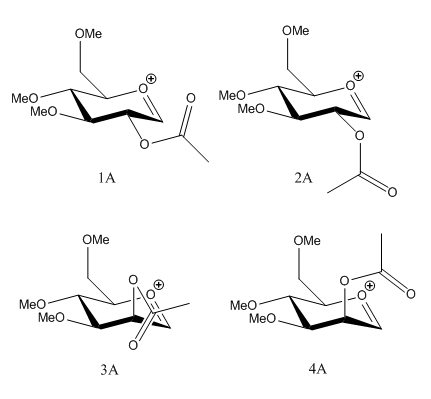
The first step of glycosidation involves the loss of a leaving group at the anomeric carbon. The resulting oxonium intermediate is planar so there is equal probability of SN1 nucleophilic attack from top and bottom face. The neighbouring group effect can control the regioselectivity issue by essentially blocking the attack of nucleophile from one face, which leads to the formation of the trans-product⁵. Firstly, four conformers of the lowest energy found were investigated. Energy was minimised using MM2 and heat of formation was also found using MOPAC.

Parameter	Molecule 1A	Molecule 2A	Energy Difference	Molecule 3A	Molecule 4A	Energy Difference
Stretch	2.1897	2.2463	0.0566	2.4135	2.5136	0.1001
Bend	10.5951	9.8645	0.7306	11.5412	14.8334	3.29228
Stretch-Bend	0.8251	0.8005	0.0246	0.9671	1.0882	0.1211
Torsion	1.3840	1.3783	0.0057	0.3157	1.9530	1.6373
Non-1,4 VDW	-3.8012	-2.9338	0.8674	-1.5602	-1.5066	0.0536
1,4 VDW	18.9398	19.2928	0.353	18.0160	17.7991	0.2169
Charge/Dipole	-0.4433	-11.0357	10.5924	-10.0768	4.8648	14.9416
Dipole/Dipole	4.4460	5.9075	1.4615	7.1479	5.8223	1.3256
Total energy	34.1352	25.5203	8.6149	28.7644	47.3679	18.6035

Energy	Molecule 1A	Molecule 2A	Energy Difference	Molecule 3A	Molecule 4A	Energy Difference
Heat of Formation	-66.72260	-67.48977	0.76717	-66.66579	-56.78597	9.87982

1A and 2A have the acetyl group at the equatorial position and 3A and 4A have the acetyl group at the axial position. The acetyl group in 1A and 4A point away from the aromatic ring and it points towards the aromatic ring in 2A and 3A. For the two equatorial acetyl conformers, the one that points towards the ring is lower in energy; 2A is lower in energy by 8.6149 kcal/mol compared to 1A. This is also true for the axial acetyl conformers. Acetyl group pointing towards the ring shows extra stabilisation; 3A is lower in energy by 18.6035 kcal/mol compared to 4A. This can be due to increased orbital interactions between the acetyl group with the oxonium cation. Another possible explanation is related to charge dipoles. The closer the acetyl group to the oxonium cation, the smaller the charge dipole thus molecule is more stabilised. For the two equatorial isomers, 1A has a larger charge dipole compared to 2A so 1A is less stable, hence it has a greater energy. The same can be observed from the axial isomers, with 3A having a more stable charge dipole energy compared to 4A, which has a higher energy. The MOPAC calculations also agrees with that of the MM2, with 2A and 3A being lower in energy compared to 1A and 4A respectively.

The table below shows the distances between the O atom in the acetyl group and the anomeric C atom. Clearly for the less stable structures (1A and 4A), the distances are larger than that of the more stable isomers (2A and 3A). Larger distances means increased difficulty of attack from the oxygen atom to the anomeric C atom. The increased distances may also contribute to lower orbital interactions and higher charge dipoles, both of which are the causes of the increased in energy.

Parameter	1A	1B	1C	1D
Bond Distance	3.9	1.7	1.6	4.3

1A

1B

1C

1D

The intermediate where the carbonyl oxygen has formed a bond to the anomeric carbon is also investigated. The four conformers, 1B, 2B, 3B and 4B (lowest energy isomers that i could find), also show similar trend to the previous isomers. This is 2B and 3B being more stabilised compared to 1B and 4B respectively, although the energy difference is less than that observed from above. Again, the charge dipoles of 2B and 3B are smaller than 1B and 4B respectively, leading to lower total energy of the molecule. MOPAC calculation also shows the same trend, with 2B and 3B being lower in energy compared to 1B and 4B. Having investigated the reactant and product energies, it can be concluded that the neighboring group effect is not favourable for 1A and 4A as both of these and their resulting products have higher energy. Therefore the formation of the β-anomer (trans product) is very favourable due to lower energy (ie 2A and 3A).

Parameter	Molecule 1B	Molecule 2B	Energy Difference	Molecule 3B	Molecule 4B	Energy Difference
Stretch	2.6510	2.4321	0.2189	2.5825	2.6681	0.0856
Bend	17.4406	16.2919	1.1487	16.6213	17.0389	0.4176
Stretch-Bend	0.7645	0.5937	0.1708	0.7165	0.7341	0.0176
Torsion	7.6820	5.5953	2.0867	6.9043	6.0528	0.8515
Non-1,4 VDW	-2.6350	-2.9863	0.3513	-2.6800	-2.3999	0.2801
1,4 VDW	19.3863	17.7296	1.6567	19.3842	19.0560	0.32282
Charge/Dipole	4.4279	-3.1189	7.5468	-2.5800	1.5020	4.0820
Dipole/Dipole	-0.5301	-4.1735	3.6434	-0.8757	0.2787	0.5970
Total energy	41.6404	39.9107	1.7297	40.0721	44.9307	4.8586

Energy	Molecule 1B	Molecule 2B	Energy Difference	Molecule 3B	Molecule 4B	Energy Difference
Heat of Formation	-66.72260	-67.48977	0.76717	-66.66579	-56.78597	9.87982

week 2

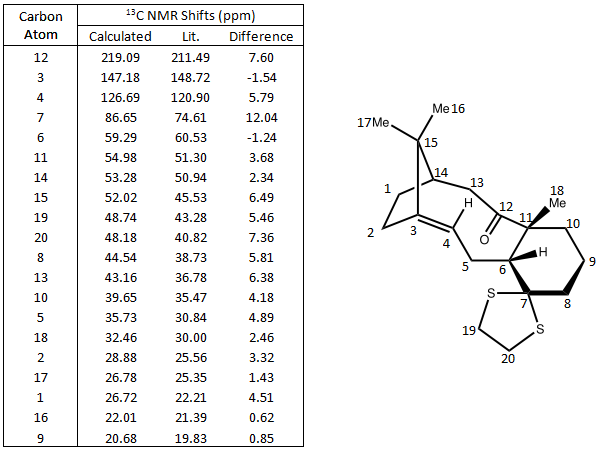
¹³C NMR Prediction

¹³C and Taxol derivative (molecule 18) was predicted and compared against literature values. The calculated chemical shifts generally fit well with data. The biggest error is at carbon number 7, which is bonded to the dithiane group. Other chemical shifts are mostly within 5ppm, except for some special cases such as the carbonyl carbon and those bonded to one S atom. DOI:0042/22255

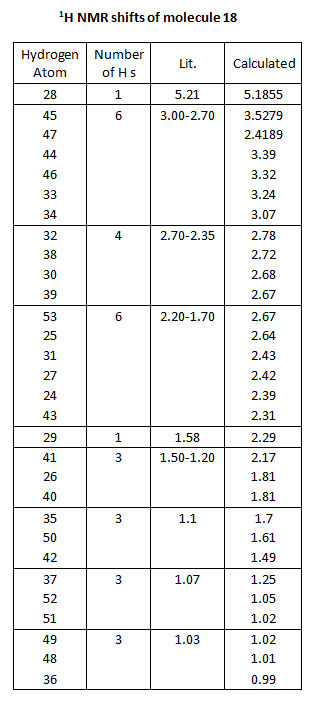
¹H NMR Prediction

Picture showing H numbers:

Table showing H numbers, literature and calculated shifts:

The calculated and the literature values of the chemical shifts correspond well. A lot of the predicted values are slightly larger than that of the literature.

Literature Project

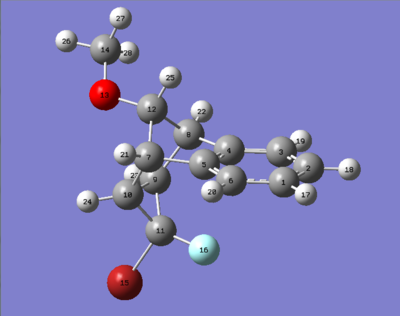
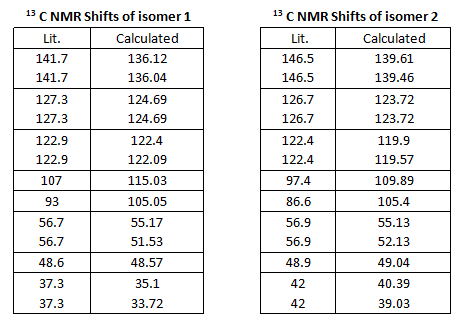
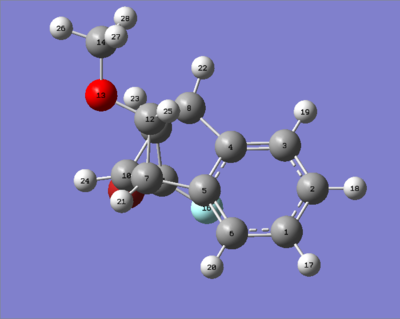
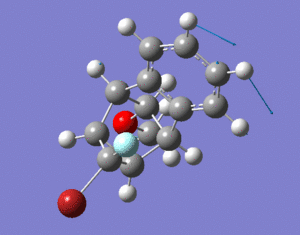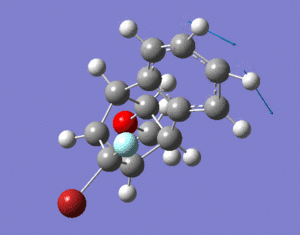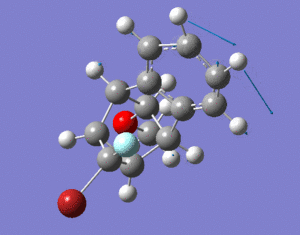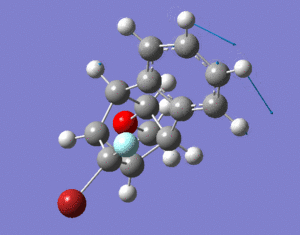
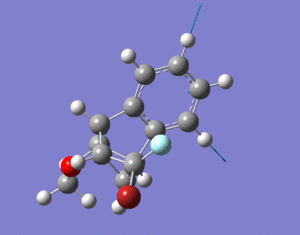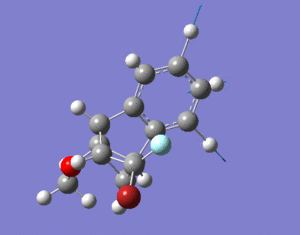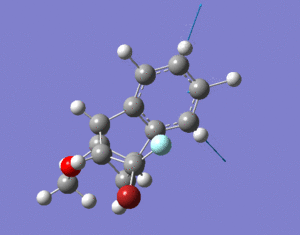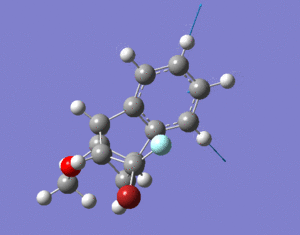
The two isomers shown below were investigated in this project. The aromatic structure consists of two halogens, Br and F. The way these halogens are arranged determine the structure of the isomers. Isomer 1 is when Br is under the aromatic ring and isomer 2 is when F is under the aromatic ring. Energy minimisation calculations were performed using MM2, MMFF94 and MOPAC^[2].

isomer 1

1A

isomer 2

1A

Parameter	Isomer 1	Isomer 2	Energy Difference
Stretch	2.6111	2.3838	0.2273
Bend	34.7915	30.2498	4.5417
Stretch-Bend	-1.6059	-1.5350	0.0709
Torsion	2.9995	3.1306	-0.1311
Non-1,4 VDW	-0.9756	--1.7219	0.7463
1,4 VDW	10.8740	11.9443	-1.0703
Dipole/Dipole	0.6264	0.6260	0.0004
Total energy (kcal mol^-1)	49.3210	45.0774	4.2436

Isomers/Energy	MMFF94	Heat of Formation
Isomer 1	97.0042	-9.36096
Isomer 2	92.9239	-10.25135

From these data it can be seen that isomer 1 has higher energy than isomer 2. The biggest contribution to the difference in energy is bending energy; isomer 1 is higher than isomer 2 by 4.5417 kcal/mol. This can be due to the slight increase in steric clash between the larger Br atom and the aromatic structure. The increase in repulsion increases the angle of the C-C-Br bond to 129 deg (shown in diagram below). The C-C-F bond angle is smaller than that (125 deg) as it experiences less repulsion, which is closer to the idea angle 120 deg. The larger the bond angle the more strain the molecule has and so isomer 1 is higher in energy. The MMFF94 and MOPAC calculations all agree with that of MM2, with isomer 1 being higher in energy compared to isomer 2.

Another conformer (press to see mol file) was found with energy 48.1659 kcal/mol. Other conformations only differ in energy by 1 d.p. therefore is not included here. The details of the conformer is outlined below. Its bending energy is in between that of the two isomers above, and so is the total energy. This indicates the importance of bending energy has on the total energy of the molecule.

  Stretch:                2.3671
  Bend:                  33.9513
  Stretch-Bend:          -1.4393
  Torsion:                1.7270
  Non-1,4 VDW:           -0.4999
  1,4 VDW:               11.2037
  Dipole/Dipole:          0.8558
Total Energy:            48.1659 kcal/mol

¹³C NMR

Isomer 1 DOI:10042/22193 DOI:10042/22194

molecule of isomer 1

¹³C NMR Spectrum of isomer 1

Isomer 2 DOI:10042/22196 DOI:10042/22195

molecule of isomer 2

¹³C NMR Spectrum of isomer 2

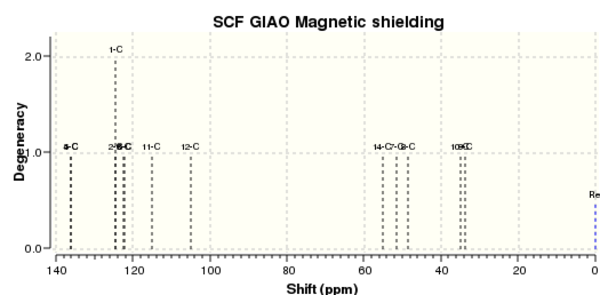
¹³C NMR were predicted and compared against those in literature. All the calculated values agree well (some even up to 1dp) with the literature values. The difference between the chemical shifts are large enough for the two isomers to be identified. Degenerate orbitals are indicated by the boxes. The ¹³C NMR spectra have very close resemblance of each other.

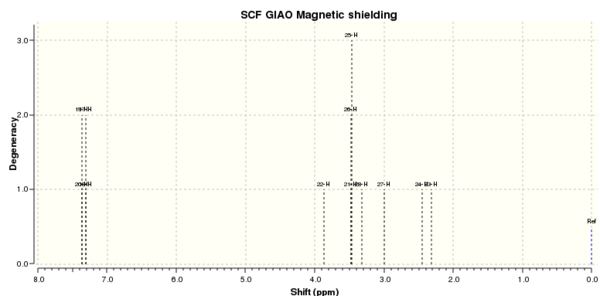
¹H NMR

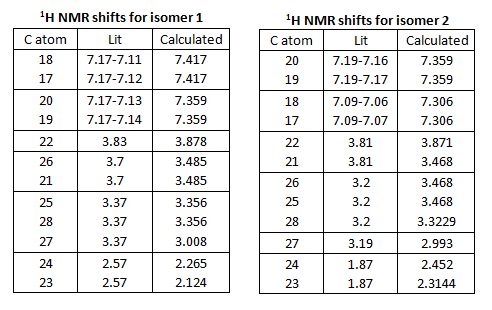
¹H NMR is also calculated and compared against literature.

isomer 1 with H labels

¹H NMR spectrum of isomer 1

isomer 2 with H labels

¹H NMR spectrum of isomer 2

The calculated and literature chemical shifts are summarised below. To find the H atom responsible for the shift, refer back to the two diagrams of the isomers with number labels. Looking at the values of the shifts, the numbers generally have a good match to those from the literature. The boxes indicate degeneracy according to literature (ie for isomer 1, H atoms 18 and 17 are degenerate according to literature as they are in the same box). From literature, H atoms 25, 28 and 27 in isomer 1 are degenerate (all are 3.37). However, according to the calculated shifts, only two of these energies are degenerate (3.356) and the last one is not (3.008). Other examples like this can be found in isomer 2. However the difference is very small and so the computed calculation are still good predictions. Comparing the shifts for the two isomers, all the values are very close together, although there is a small difference, ¹H NMR may not be the best technique to differentiate the two isomers.

Optical Rotation

Isomer 1 and 2 are diastereoisomers as the top chiral centre (top of carbon bridge) is common for both. This means that the isomers would give different optical rotation, since they are not mirror images of each other. After performing calculations, it was found that isomer 1 has optical rotation of -48.62 deg whereas isomer 2 has -82.68 deg, nearly double of isomer 1. With such a large difference in value, optical rotation would be one of the key spectroscopic differences of the two isomers.

isomer 1 DOI:10042/22206

isomer 2 DOI:10042/22207

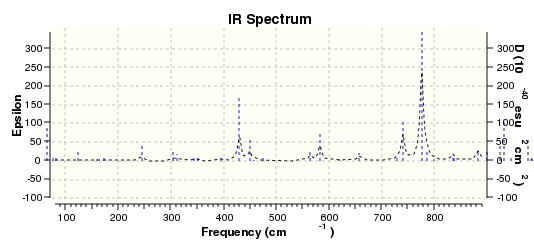
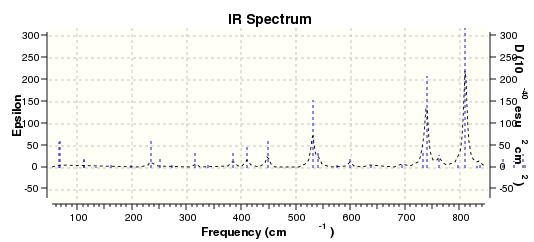
IR

IR calculations were also performed. The energy difference between the two isomers is extremely small. Isomer 1 has 2038828.56 kcal/mol and isomer 2 has 2038830.59 kcal/mol. By inspecting the two IR spectra, you can see that a lot of peaks do not coincide. Three vibrational examples were picked out for comparison. Looking at the two IR tables below for the two isomers, the C-O stretches have different frequencies and intensities. For isomer 1, it has a higher frequency, at 1255.56 Hz, with intensity 52.5002. Whereas for isomer 2 it has a lower frequency, at 1150.32 Hz, with a much higher intensity 176.5924. At frequency of 1508.41 Hz, both isomers have benzene C-H stretches. However the modes are different which can be seen by looking at the animations. Lastly, at around 3117 Hz both isomers have the same kind of benzene asymmetric stretch, with relatively low intensities.

IR spectrum of isomer 1 DOI:10042/22192

IR spectrum of isomer 2 DOI:10042/22191

IR table of Isomer 1:

Frequency	Intensity	Form of Vibration	Animation
1255.56	52.5002	C-O stretch
1507.15	3.8584	Benzene C-H stretch
3117.50	1.2248	Benzene Asymmetric Stretch

IR table of Isomer 2:

Frequency	Intensity	Form of Vibration	Animation
1150.32	176.5924	C-O stretch
1508.41	5.6239	Benzene C-H stretch
3117.93	0.6240	Benzene Asymmetric Stretch