Physical Computational Lab - Transition States

Cope Rearrangement

The Cope Rearrangement is a pericyclic reaction of the type; [3,3] sigmatropic. The reaction is a concerted, cyclic rearrangement of 1,5 hexadiene which involves 6 electrons (4n+2) through a Huckel transition state. The reaction can occur through both Boat and Chair conformation transition satates with the Chair being of lower energy.

Optimising Reactants and Products

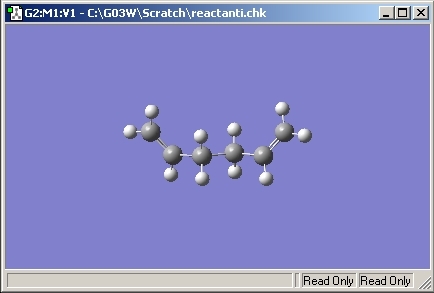
The Hartree-Fock method was then selected along with the 3-21G basis set. The first molecule was drawn in Gaussview and cleaned to improve the calculation time. As per instructions, the anti conformation of 1,5 hexatriene was drawn. The calculation was run and compared to the results table in appendix 1.

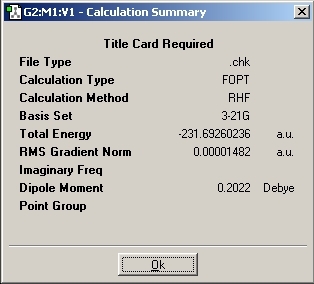
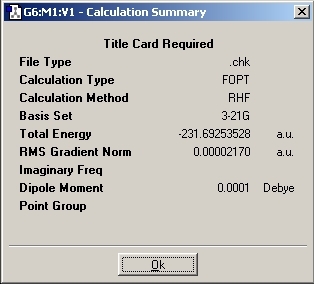
The symmetry of the molecule was found to be C2 which corresponds to the anti-1 conformation given in Appendix 1. The energy was found to be -231.692602 which is the same as quoted in Appendix 1.

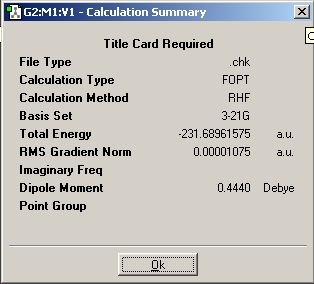
The next part of the experiment required the gauche conformation to be calculated. The diagram below shows the geometry. The same calculation method was run and the results given below.

The symmetry of the conformation was found to be C1 which corresponds to gauche-5 in Appendix-1. The energy was found to be -231.689616 which is the same as quoted in Appendix-1.

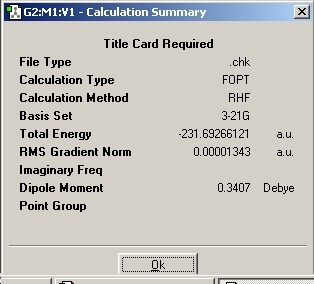
The conformation with the lowest energy was then predicted drawn. The gauche-3 conformation was found to be the lowest with an energy of -231.69266 and C1 symmetry.

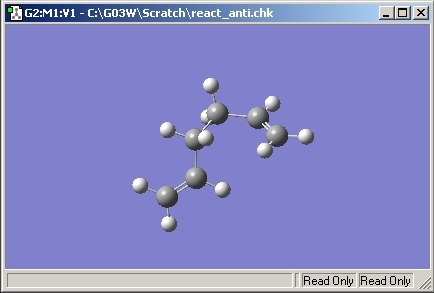
The C_i anti 2 conformation was then drawn and optimised. The results are given below.

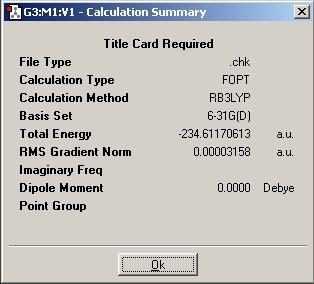
To improve the accuracy and reliability of the calculations, the method was changed to B3LYP with the 6-31G(d) basis set.

As can be seen from the results summary, the energy was dramatically lowered by changing the method calculation and basis set. The main difference by changing to the B3LYP calculation is the geometry of the molecule.

Frequency Analysis

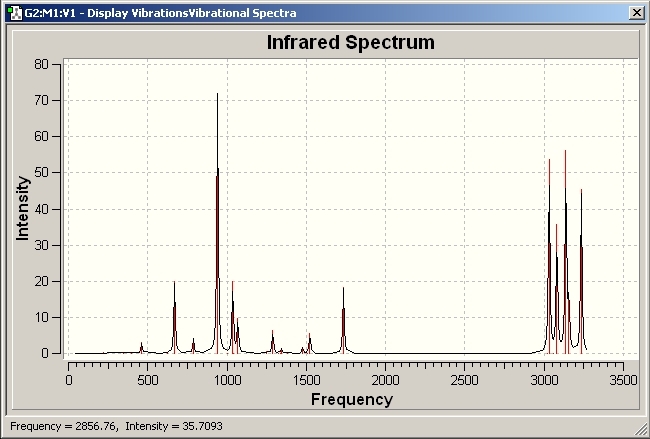
The vibrations of the molecule were then investigated and 42 vibrations for this molecule were observed. All vibrations were positive showing that the geometry is at a minimum although only about half of these vibrations were IR active. The spectra is given below:

Thermochemistry

The .log file of the molecule was then opened and the follwing thermochemistry data was obtained.

Energy Term	Energy at 298.15K (Hartree)
Sum of Electronic and Zero-point energies	-234.469195
Sum of Electronic and Thermal energies	-234.461847
Sum of Electronic and Thermal enthalpies	-234.460903
Sum of Electronic and Free energies	-234.500782

Optimising the Boat and Chair Transition States

The Boat and Chair conformations will be optimised using a different methods of calculation. The energies will then be compared to those given in Appendix 2.

Allyl Unit

The allyl unit, (CH₂CHCH₂), was first drawn and optimised using Gaussian so that the structure of the chair could be guessed.

Chair Transition State

The allyl unit was then copied and pasted. The structures were moved into a chair like position with the terminal carbons set to 2.2Å apart.

The Opt+Freq calculation method was used in this exercise to save time and the structure was optimised to a transition state, TS Berny. "noeigen" was entered into the calculation to ensure only one transition state was calculated.

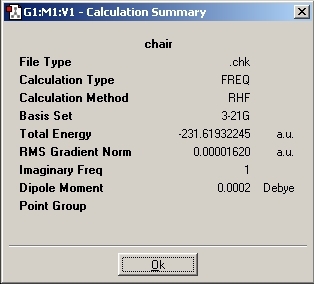
The results show that the chair transitiom state has an energy of -231.61932 Hartree with a C_2h symmetry point group.

However, the terminal carbons both have different bond distances (2.0197Å and 2.0201Å) which will be further optimised below. The vibrations of the molecule show an imaginary frequency at -817.9cm^-1. This vibration shows the bond making/breaking involved in the transition state.

The Redundant Coordinate Editior was used for this calculation to fix the position of the terminal carbons. The same allyl structure was used for this calculation with the Hartree-Fock method and 3-21G basis set. The bonds were then frozen and the calculation run.

Boat Transition State

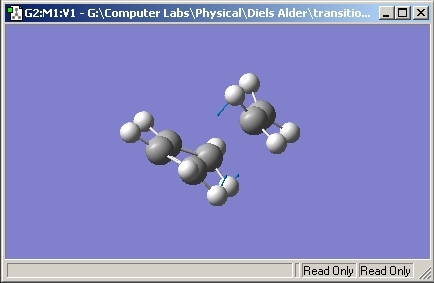
Th allyl fragment which was used for the chair conformation was again used for the boat conformation. Again the fragment was copied and then pasted beofre being moved to a boat like conformation. The optimisation was set up with the QST2 method being used. However, the first calculation failed and a chair like structure was seen. The dihedral angle was then modified as per the script and a boat like reactant was set up. Each atom was also labelled:

This was then optimised and a boat conformation transition state was achieved.

The Boat conformation was found to have an energy of -231.60280 Hartree with a C_2V point group. The terminal carbons were found to be 2.14Å away from each other.

From the results above, it can be said that the Chair conformation is the most favourable transition state for the Cope rearrangement. The energy of the chair transition state is approximately 43kJ/mol lower than that of the Boat conformation and the terminal carbon bond distances are also closer to those observed in C-C bonds (1.54Å)

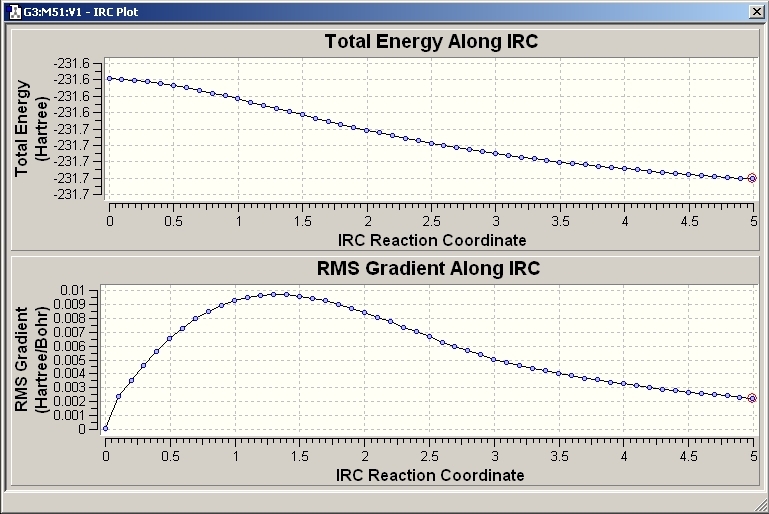
IRC Method

The checkpoint file can then be used to show that change in structure through small steps. The IRC graph is opened and from this the minimum energy point in the transition state can be found.

Activation Energies

Inorder to compare the energy between the boat and chair transition structure, the optmisation calculations had to be run at the more accurate B3LYP method with 6-31G(d) as a basis set. The resultant energies were very different to the HF method. A comparison of the energies can be seen below.

Energy	Chair	Boat	Reactant
Sum of Electronic and Zero-Point energies	-234.414927	-234.402332	-234.469195
Sum of Electronic and Thermal Energies	-234.409005	-234.396005	-234.461847

The activation energy was then calculated from the difference between the zero-point energy and the reactant energy. The results were then compared to experimental values:

Conformation	B3LYP at 0K	Expt.
Boat	41.95	44.7 +/- 2.0
Chair	34.05	33.5 +/- 0.5

As can be seen from the table above, the calculated energies are close to the experimental energies making the B3LYP method an accurate calculation. The energies have been given to 2 d.p. but the results would have error and are probably only accurate to +/- 1 kcal/mol at most.

Diels Alder Cycloaddition

Cis Butadiene and Ethene

Here we will look at the pericylic reaction between cis butadiene and ethene:

The HOMO and LUMO orbitals will be investigated as there must be interaction between the HOMO of one reactant and the LUMO of another inorder for the reaction to occur.

The cis butadiene molecule was drawn in Gaussview and optimised with frequency using the semi-emperical AM1 method. From this calculation the HOMO and LUMO orbitals of the molecule could be seen.

HOMO

The HOMO orbital of Cis Butadiene is shown below and is Antisymmetric.

LUMO

The LUMO orbital of Cis Butadiene is shown below and is Symmetric.

The same calculation was then run for Ethene. Again the HOMO and LUMO orbitals were plotted.

HOMO

The HOMO orbital of Ethene is shown below and is Symmetric.

LUMO

The LUMO orbital of Ethene is shown below and is Antisymmetric.

The fragements were then added to one window and a product like structure was created. The terminal carbons were set to 2.2Å. The Semi-Emperical AM1 method was first used and optimised to transition state Berny. The structure was then used again for further optimisation using the most accurate HF method with the 3-21G basis set.

By first looking at the product, it is possible to say that there is a bonding interaction between the terminal carbons in this transition state. Although the bond distance was found to be 2.209Å, this is considerably shorter than the sum of the Van der Waals radius indicating a covalent bonding interaction. The bond distance is much bigger than the sp² bond distance of 1.34Å and the sp³ bond distance of 1.54Å suggesting a very weak bond.

The vibrations of the molecule were then investigated with the hope they would provide an explanation about the terminal carbon bonding.

Imaginary Vibration

As this is a transition state calculation there is a negative vibration as expected. The vibration shows the making of the bond between the two terminal carbon atoms with a frequency of -818cm^-1.

First Positive Vibration

The first positive vibration was seen at -167cm^-1 and shows the ethene fragment twisting. This vibration shows no bonds forming.

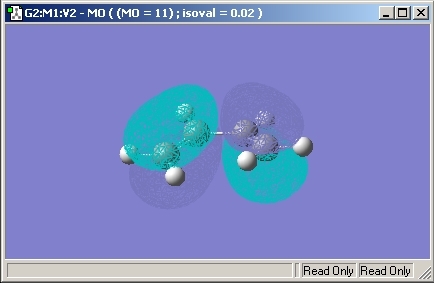
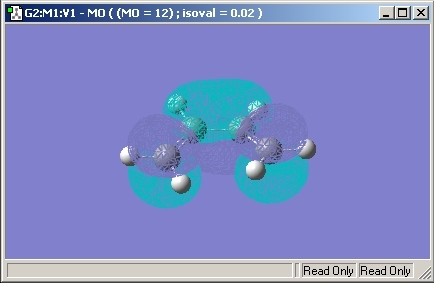
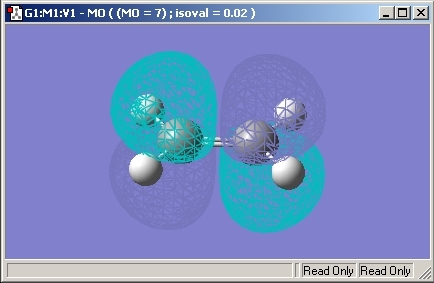
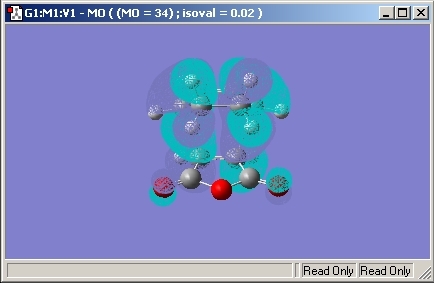
Molecular Orbitals

The Molecular Orbitals of the transition state were then investigated and are shown below.

The HOMO and LUMO Orbitals are both symmetrical through a verticle plane in the molecule.

HOMO

LUMO

Looking at the molecular oribtals of the porduct, it is possible to say that the transition state molecular orbitals must have constructive overlap. Therefore, the same symmetry element would be expected for both the reactants and the transition state.

As the HOMO given in the transition state has symmetric molecular oribtials, it is therefore the wrong MO. The bonding interaction would be expected to be between the electron rich HOMO (butadiene) and the electron poor LUMO (ethene). The HOMO also shows a node which shows that no bonding is present.

It was then noticed that the HOMO and HOMO-1 were very close in energy to eachother and that the HOMO-1 could possible be the bonding orbital as the Hartree Fock calculation isn't the most accurate available. By looking at the MO and comparing it to the seperate MO's of butadiene and ethene, it is possible to see that there is a bonding interaction.

HOMO-1

The HOMO-1 orbital is Asymmetric

The HOMO-1 molecular orbital is therefore infact the HOMO orbital. However, the calculations were not accurate enough to distinguish between the two orbitals and so a more accurate calculation would be needed to explain this observation.

Cyclohexa-1,3-diene Reaction with Maleic Anhydride

This pericylic cycloadditon reaction can form two different conformations; exo and endo. The reactants both have the same energy and both form a transition state so the reaction is either kinetically or thermodynamically driven. The transition state with the lowest activation energy will therefore be the kinetic product. Infact, this reaction is kinetically favoured and so the lowest activation energy barrier will be the prodominent product.

The molecular is more complex than the previous reaction but the Hartree Fock and 3-21G calculation method and basis set should be adequate to explain this reaction. The geometries and molecular orbitals are shown below:

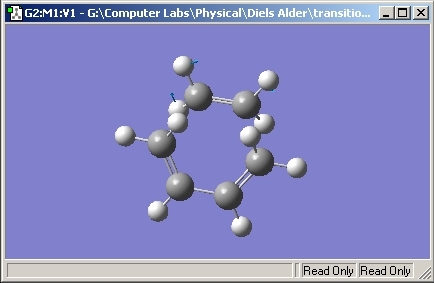
Endo

As we are interested in the activation energy, the Sum of the Electronic and Zero-Point energy was found to be -605.408. The bonds made in the transition state were found to be 2.23Å in length.

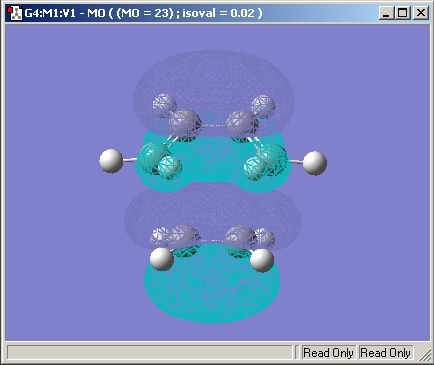
The HOMO molecular orbital is given below.

Exo

Again, the same calculation was used and the Sum of the Electronic and Zero-Point energy was found to be -605.415. The bonds made in the transition state were found to be 2.26Å in length, longer than the Endo conformation.

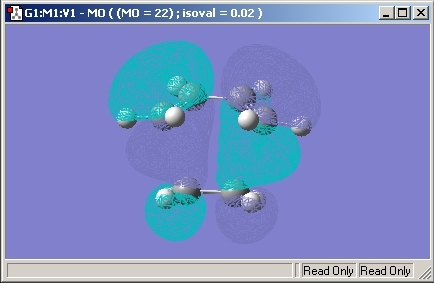
The HOMO molecular orbital is given below.

By comparing the two energies, it was found that the Endo transition state has an activation energy that is approximately 17kJ/mol lower in energy than the Exo conformation.

By looking at the MO's and using the carbon bond distance, it is possible to say that the Endo conformation is the lowest in energy. There is more hindrance for the attacking anhydride in the Exo conformation and so a longer C-C bond is observed. Both of the MO's obtained have antisymmetric orbitals. Looking in more detail at the Endo MO, there is a stabilising overlap. There are two orbitals on the cyclohexadiene (possibly π*) which interact with two orbitals on the Anhydride (possibly π* and Oxygen lone pair). These orbitals are not involved in the actual bonding of the new carbon bonds and so are known as secondary orbital stabilisations. This interction is not present in the Exo conformation and so there are no stabilising secondary orbital overlaps causing it to have a higher energy compared to the Endo conformation.