Rep:Mod:jrb061411

Computational Chemistry - Inorganic

Introduction

The types of calculations used throughout this computational experiment are Vibrational analysis calculations. These are second derivative functions of the potential energy surfaces (PES) with respect to the bond length of the equilibrium geometry. The calculation optimises the geometry of the product and the output provides information regarding the states of the molecule; i.e. is the ground or transition state the most stable. The output of these calculations allows for the vibrational frequencies to be investigated. The BH₃ molecule was first used to gain an insight in the nature of the Gaussian programme and the type of analysis required before moving onto the more complicated molecules. The BCl₃ was the first molecules investigated.

BCl₃

Optimised Geometry

Before the vibrational features of the molecule could be calculated, the molecule had to be optimised using the B3LYP calculation with the LanL2MB basis set. This basis set is a higher basis set used compared to BH₃ due to the electronic nature of the Cl atoms. As a second row element, the p orbitals must be taken into account to gain a more accurate result.

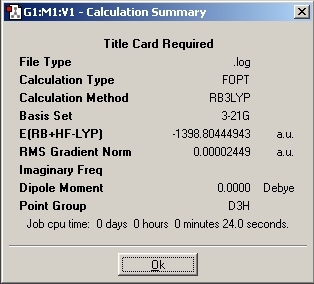
The calculation was run on the laptop and the following information was gained from the output file:

	Result
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2MB
Energy	-69.43928
RMS Gradient	0.00005905
Dipole Moment	0.00 D +/- 0.01
Point Group	D3H
Time	11 s

Using tools available in Gaussian, the equilibrium B-Cl bond length and the Cl-B-Cl bond angle were calculated:

B-Cl Distance = 1.87 Å +/- 0.01 Å

Bond Angle = 120.0^o +/- 0.1 ^o

The angle was 120^o as expected and as confirmed by literature. However, the bond length was higher than expected for this optimisation so the basis set was changed and the calculation was re-run. As the molecule was optimised once, the calculation was fast.

It can be seen that this optimisation dramtically reduced the total energy of the molecule producing a B-Cl bond much closer to the literature value of 1.74Å. Therefore, as an distance of 1.775Å was acheived, the computer modelling calculations are only accurate to 2d.p.

As with any calculations, there will be errors involved with the results are the output file produces a number. This number can be taken to many decimal places but this is unnecessary as the computer calculations aren’t that accurate. The energies generated are only accurate to 3.8E-4 Hartree which is approximately 1kJ/mol.

Vibrations

After the optimisation was run, the calculation was changed to frequency so that the vibrations of the molecule could be seen.

	Result
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2MB
Energy	-69.43928
RMS Gradient	0.00005910
Dipole Moment	0.00 D +/- 0.01
Point Group	D3H
Time	11 s

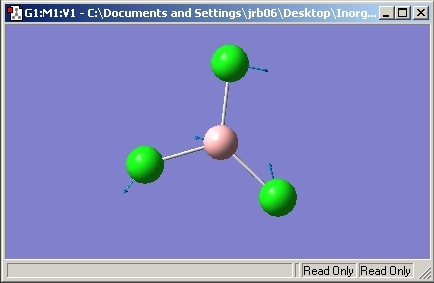
The Vibrations were then run in the Gaussian program and then snapshots were used to compute a table showing the displacement of the vibrations along with their frequency, intensity and symmetry.

Number	Vibration	Vibration Description	Frequency (cm-1) / Intensity	Symmetry
1		Vibration in plane of the molecule, one B-Cl bond vibrating	214.131 / 3.93	Asymmetric Bend, E'
2		Vibration in plane of molecule. Two B-Cl bonds are vibrating in scissor action	214.132 / 3.93	Asymmetric Bend E'
3		Boron atom moves back and forth out of the plane of the molecule	376.94 / 43.78	Asymmetric stretch A2
4		Boron stationary. Chlorines move back and forth in plane of the molecule	417.377 / 0	Symmetric Stretch A1'
5		Boron moves from side to side in plane of molecule	939.469 / 258.67	Asymmetric stretch E'
6		Boron moves along B-Cl bond	939.470 / 258.688	Asymmetric stretch E'

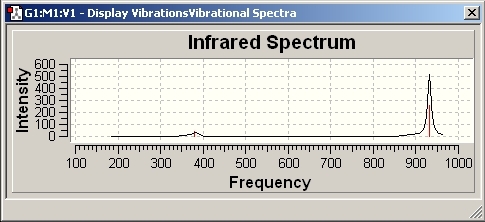
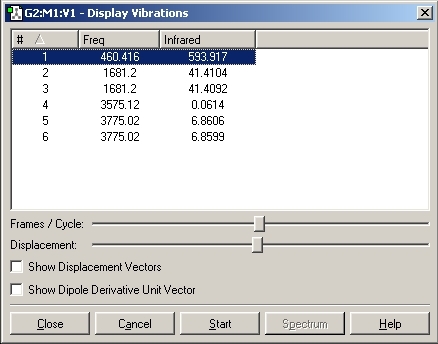
As can be seen with the vibrations, they are all positive implying that the optimised geometry of the molecule is at a minimum on the PES. There are 6 vibrations seen as a non linear molecule will have 3n-6 normal modes of vibration, where n=4.

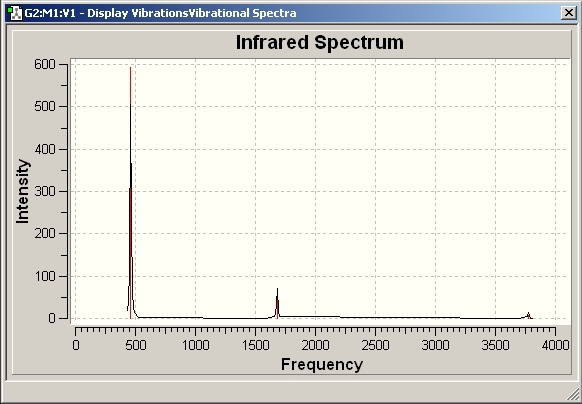
Looking at the IR spectra in more detail, it can be seen that there are less than 6 peaks. This is because the Infra Red absorption frequencies are determined by the dipole moment of the bond. As the symmetric stretch, A1’, has no change in dipole moment, it doesn’t show a peak. Another important observation from the frequencies that the degenerate E’ sets are different. This is because one is the B-Cl bending vibration (214.13cm^-1) and the other is the B-Cl stretching vibration (939.47cm^-1). Stretching a bond requires more energy than bending a bond so it has a higher absorption. The stretching peak is much more intense than the bending peak as the change in dipole moment is greater.

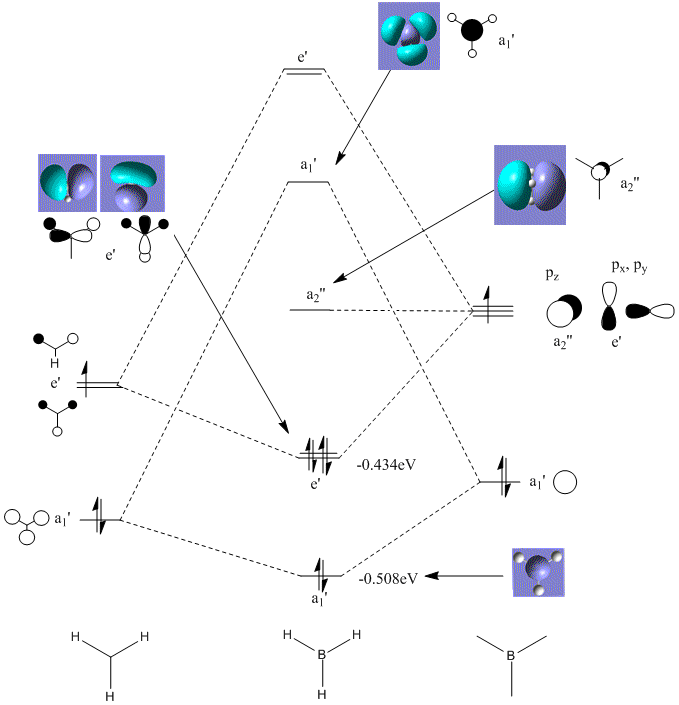
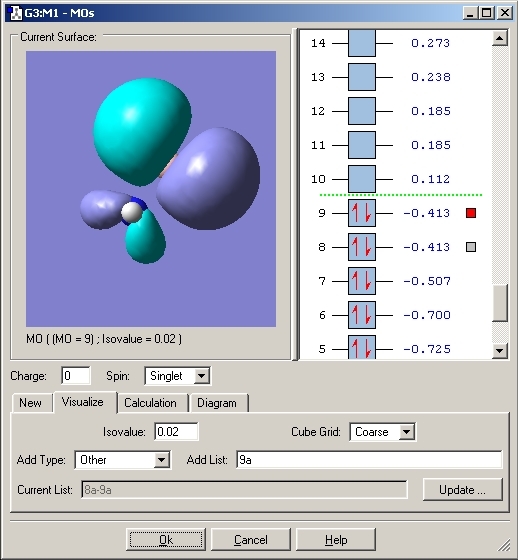
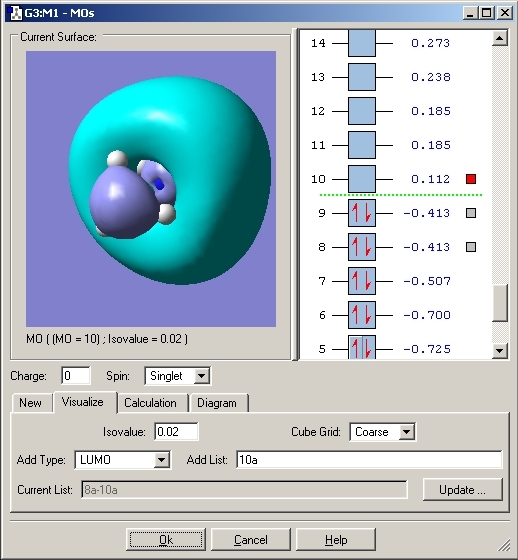
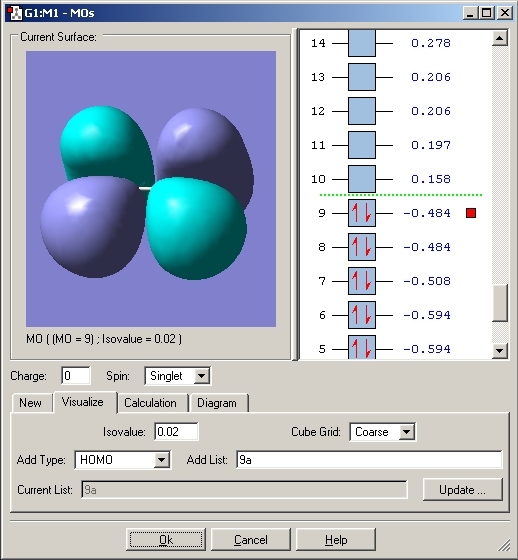
MO Diagram

The Gaussian program was then used to describe the Molecular Oribtals of BH₃. The qualitative approach to the MO's were first looked at and was constructed as taught in earlier lectures. These gave an insight into the shapes of the orbitals but a quantitative approach was also needed. The MO's were looked at in the Gaussview program and from this they were matched to the corresponding MO's (as below).

Questions

The basic shapes produced from both approaches are very similar although the quantatative approach gives a much better visualisation. The qualitative MO's can be seen to be similar as "like" phases will overlap producing shapes much more like the Gaussian MO's. Thus, this allows one to say that the Mo theory is a very powerfu, fast and accurate description of molecular oribtals.

For molecules to become stable they must complete their octet or electrons, thus BH₃ needs two more electrons. As BH₃ is Lewis acidic, it can be seen that the a₂" orbital offers a large and broad area above and below the plane of the molecule allowing a Lewis Base to attack easily.

An interesting point about using Gaussview to visualise the orbitals is that it produced 4 MO's. The one which was left out was significantly lower on energy than the others and can only be explained as a weakness in the prediction.

Small Molecule - H2O

Optimised Geometry

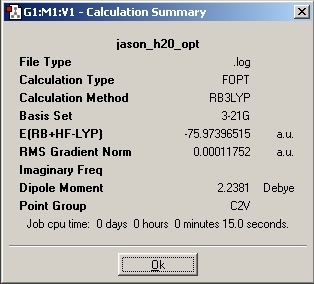
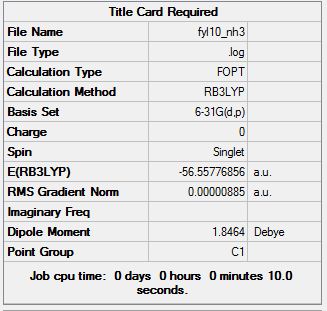
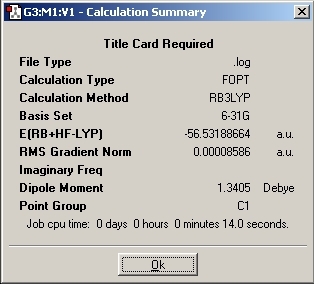
As this small molecules contains atoms in the first row of elements only, a 3-21G basis set was used for the optimisation. Although 3-21G has a lower accuracy than the LANL2MB basis set used in the previous exercise, H₂O only requires a small number of mathematical functions.

From the optimised structure, the bond length and angle for H₂O was analysed.

O-H Distance = 0.99 Å +/- 0.01 Å

Bond Angle = 103.9^o +/- 0.1 ^o

As with the BCl₃ molecule, the computed values are close but not the same as the literature values. The bond angle is close to literature (104.45^o) but the bond distance is a little more inaccurate (0.958Å). This is because the 3-21G basis set is a very simple mathematical calculation.

The molecule was uploaded with the following D-Space Link: DOI:10042/to-1918

Vibrations

Number	Vibration	Vibration Description	Frequency (cm-1) / Intensity	Symmetry
1		O-H bonds move in a scissoring action	1692.47 / 36.74	Asymmetric Bend A1'
2		Hydrogens move along the O-H bond in-time with each other	3412.4 / 13.71	Assymmetric Stretch A1
3		Hydrogens move towards the oxygen along the bond. They are out of time to each other	3553.34 / 1.56	Asymmetric stretch B12

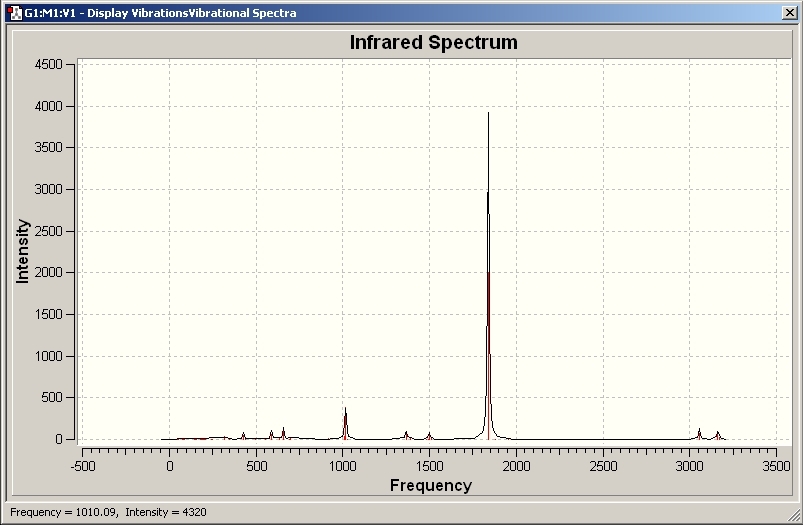
The vibrations can then be plotted on a graph as shown below. The spectra shows 3 different peaks for H₂O althought one of the peaks is very weak. This is because all of the stretching frequencies are IR active as there is a change in dipole for each vibration.

As can be seen from the spectra above, there are three normal modes of vibrations which is expected using the 3n-6 formula. All of the frequencies are positive implying that the optimisation of the molecule is at the minimum energy ground state.

Questions

The co-ordinates for the H₂O molecule are given below.

 ---------------------------------------------------------------------					
 Center     Atomic     Atomic              Coordinates (Angstroms)					
 Number     Number      Type              X           Y           Z					
 ---------------------------------------------------------------------					
    1          8             0        0.000000    0.000000    0.110812					
    2          1             0        0.000000    0.783976   -0.443248					
    3          1             0        0.000000   -0.783976   -0.443248					

The D-Space Link for this molecule is:

Mo(CO)4L2 - (L=P(CH3)3)

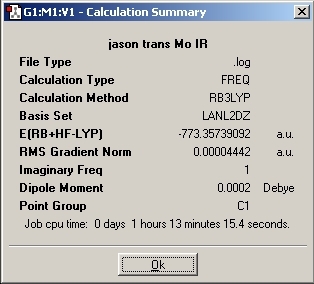
This part of the experiment investigates the transition metal complex; Mo(CO)4(PMe3)2. The cis and trans forms of the complex were investigated and compared to literature as well as each other. The molecules were first drawn as accurately as possible using the Gaussview tools to ensure an accurate input file was created. The first optimisation run used the B3LYP method and the LanL2MB basis set. This set was not accurate enough but was needed so that the more accurate LanL2DZ basis set could be run with a time that wasn’t too long. The convergence for this calculation was also set to be more tightly as the calculation involves a much higher level basis set. As Phosphorous atoms have low lying d-orbitals, these have the ability to interact with vacant p orbitals so the calculation basis set needed to be increased.

The difference with this molecule compared to the others is the need to use pseudo potentials. They are needed because the complex involves a large number of electrons. Due to the large number of electrons, the calculations had to be sent to the overnight SCAN system.

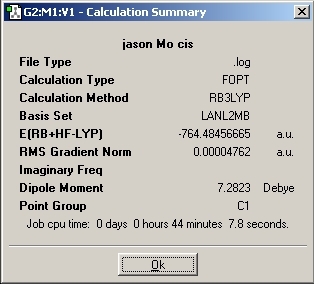
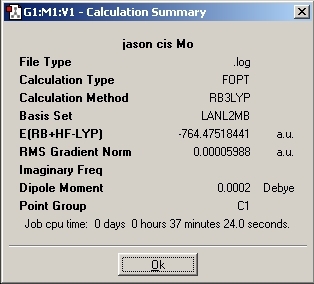
Cis Isomer

LanL2MB Optimisation

LanL2DZ Optimisation

The basis set was then changed and the calculation was resent to SCAN. The D-space link is provided.

The optimised molecules D-Space Link: DOI:10042/to-1812

Vibrations

Finally, the vibrations of the complexes were analysed using the optimised geometry. Again, these had to be sent to SCAN to ensure the calculations completed properly.

D-Space Link: DOI:10042/to-1836

Discussion

	Optimised Values	Literature Values
Mo-P	2.65Å	2.53Å
Mo-C (Cis to P)	2.03Å	2.03Å
Mo-C (Trans to P)	1.98Å	1.97Å
P-Mo-P angle	95.3o	97.5o

By looking at the above table and comparing the values to those in literature, it can be said that the computer modelling is an accurate and effective way to analyse complex molecules. The literature bond distances are similar to those gained from the modelling with the cis Mo-C bond being exactly the same as literature. The slight deviation from literature could be explained by the fact that Molybdenum contains f orbitals and the basis set used does not take these electrons into account. Again the angle is similar but not exactly the same which is probably due to the f orbitals not being taken into the interaction.

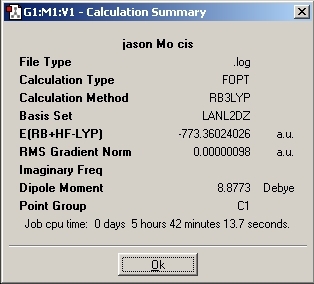
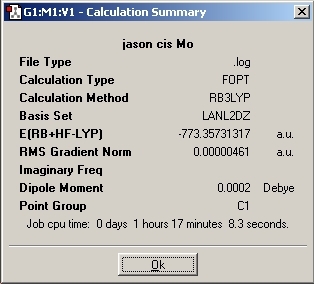
Trans Isomer

D-Space Link: DOI:10042/to-1795

LanL2MB Optimisation

LanL2DZ Optimisation

The basis set was then changed and the calculation was resent to SCAN. The D-space link is provided.

D-Space Link: DOI:10042/to-1795

Vibrations

Finally, the vibrations of the complexes were analysed using the optimised geometry. Again, these had to be sent to SCAN to ensure the calculations completed properly.

D-Space Link: DOI:10042/to-1796

Discussion

	Optimised Values	Literature Values
Mo-P	2.57Å	2.50Å
Mo-C	2.03Å	2.01Å
P-Mo-P angle	180.0o	180.0o

By looking at the above table and comparing the values to those in literature, it can be said that the computer modelling is an accurate and effective way to analyse complex molecules. The angle is exactly the same as the literature value and that would be expected as the complex is in the trans formation. The literature bond distances are similar to those gained from the modelling. The slight deviation from literature could be explained by the fact that Molybdenum contains f orbitals and the basis set used does not take these electrons into account.

Comparing the two isomer energies, the cis isomer is 7.69kJ/mol lower in energy compared to the trans isomer, making it the most stable of the two isomers.

Vibrational Analysis

Looking at the vibrational analysis and in more detail the infra red spectra of the two complexes, the C=O is the most intense of all the infra red active vibrations.

Cis

The Infra Red for the cis complex produces 4 intense C=O vibrations:

1848.46cm^-1

1850.71cm^-1

1869.94cm^-1

1960.43cm^-1

Trans

The Infra Red spectra for the trans complex produces two very intense peaks which overlap on the spectra:

1839.21cm^-1

1839.41cm^-1

NH3

Ammonia was studied as it has the ability to tunnel between Potential Energy Surfaces. This means that the molecule can invert causing creater symmetry. This inversion process is very similar to the SN2 reaction inversion. Due to this ability, a C_3V symmetry product is seen with a transtion state of D_3H.

The calculations were run for each molecule using the B3LYP calculation and 6-31G basis set.

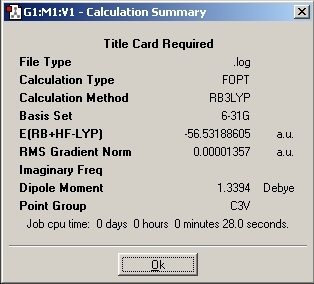
C3V Optimisation

C1 Optimisation

One of the N-H bonds was set to 1.01A so that the symmetry was locked to C1. This would cause the Gaussian program to work the molecular calculations out and not take shortcuts as it does with symmetrical molecules.

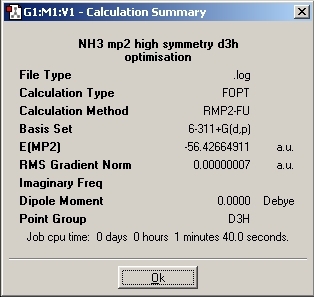
D3h Optimisation

The transition state was then investigated and a "dummy" atom was inserted to lock the symmetry to D_3H.

Questions

1. If the symmetry of the molecule us changed then the final structure of the molecule will also be different. The C_3V and C₁ symmetries have a trigonal pyrimidal structure where as the D_3H has a trigonal planar structure. Changing the rotational symmetry of the molecule does not effect the structure but mirror planes and rotational axis do. The introduction of the dummy atom causes there to be more σh planes and three new C₂ axis. These are perpendicular to the principal C₃ axis which causes the symmetry to become D.

2. By changing the symmetry of the molecule, the time taken to optimise the geometry also changes. The difference between the two C group symmetries is quite small compared to the D group symmetry. As the symmetry increase, the time increase (14s to 28s to 1min 21s)

3. The calculations work from the VSEPR predicted symmetry which is C_3V. Thus deviating away from this symmetry causes the calculation times to change.

4. The optimisation holds the symmetry throughout the calculation in the examples investigated above. Looking at the output files, the symmetry does remain constant but one would expect the calculation to be able to break symmetry if a poor input file was used.

5. By using a high symmetry structure to optimise, the calculation time should be reduced as the only the bond lengths need optimising and not the position of the atoms.

6. The lowest energy confirmation turns out to be the C₁ symmetry. However, the C_3V energy is the same to 6d.p. The computer programme produces a number and the accuracy of the model is to about 3.8E-4 Hartree which would suggest this deviation is not applicable. Thus, all three of the symmetries have the same energy to 4d.p.

7. The energy difference between C₁ and C_3V is 1.55J/mol. The energy difference between C₁ and D_3H is 905J/mol.

8. The energy difference between the two C symmetries is very small. This is because they both have the same trigonal pyramidal structure and only one bondlength is different causing the symmetry difference. However, upom changing the symmetry from C to D group and thus changing the structure of the molecule, there is a huge difference in energy. This is bacause the higher symmetry causes the the hydrogens to be closer to the nitrogen lone pair of electrons. This causes a stronger repulsion and so the energy is raised. Also the trigonal planar symmetry is not as favoured for the NH₃ molecule.

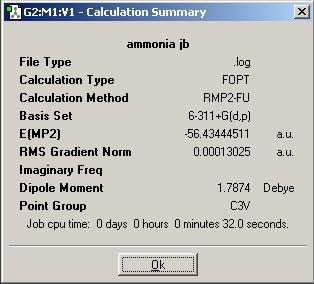
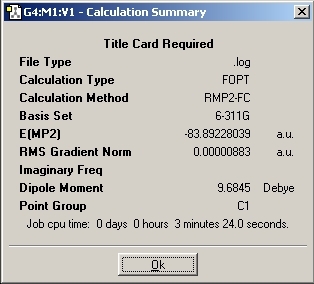
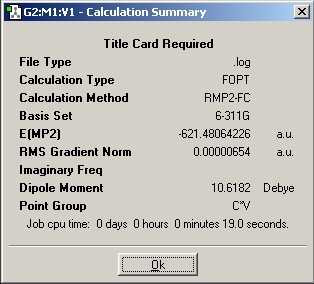
MP2 Optimisation

The optimisation method calculation was changed to RMP2-FU method and the 6-311+G(d,p) basis set was used. This change of method causes the number of mathematical calculations to increase which should improve the accuracy of the calculation.

Again, the "dummy" atom was added to the molecule to lock the symmetry so that D_3H point group was achieved.

Questions

1. Both of these calculations took longer than the previous B3LYP method as the mathematical complexity was increased.

2. The energy difference for the inversion is: 20.47kJ/mol

3. By changing the calculation method, there has been a huge increase in the energy difference. The energy change has changed from 0.905kJ/mol to 20.47kJ/mol.

4. The B3LYP method cannot be compared to literature as it is orders of magnitude different. THe MP2 method gives a result with the same magnitude and is accurate to 1s.f. Therefore, this method does provide results accurate enough to be used.

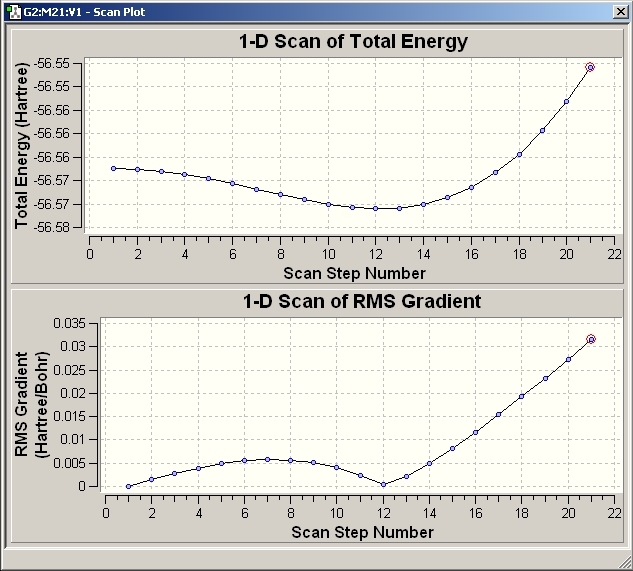
Inversion

Gaussian also has the ability to run a SCAN process which allows the inversion to take place in steps. The process can be shown on a graph of energy versus SCAN step number which is effectively the H-N-H bond. The PEs profile shows that the energy is at a minimum at step 13. The H-N-H angle at this point is measured to be 104.6^o.

Vibrations

The vibrational frequencies were then analysed from the B3LYP method optimised geometries. The spectra are shown below, along with the summary of the frequencies.

C3V Frequencies

D3H Frequencies

Questions

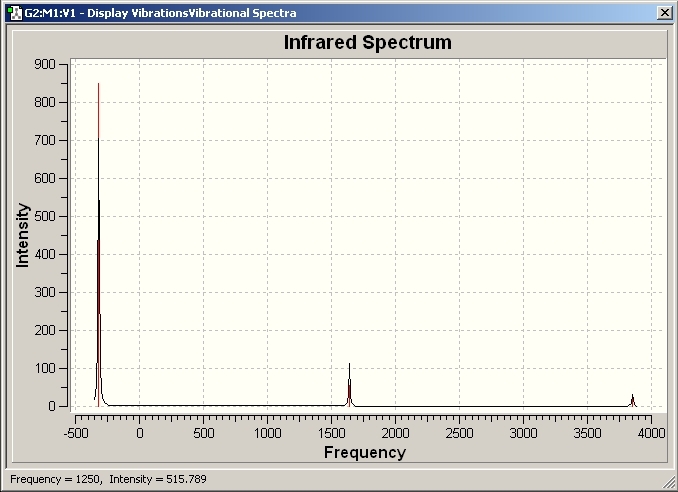
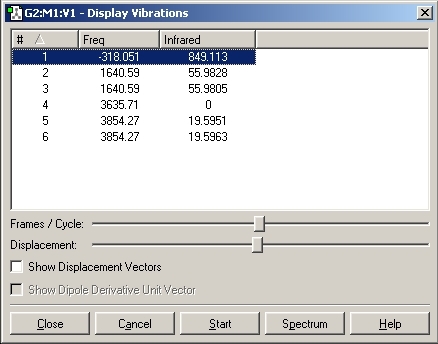
1. There are 6 positive frequencies for the C_3V structure and 5 for the D_3H.

2. As D_3H and C_3V have similar symmetry properties, the vibrations do pair up. The displacements are very similar with the only differences being due to the slightly different H-N-H bond angle. However, the A₁' should not be similar to the A₂" as this is the vibration used to follow the inversion process. This vibration is therefore expected to change.

3. The negative frequency for D_3H is seen at -318cm^-1.

4. The vibration which is lowest in frequency for both of the structures follows the inversion reaction path. For C_3V this is at 462cm^-1. and for D_3H at -318cm^-1.

Mini Project - Fuels of the Future

Introduction

With the modern world running low on fossil fuels and the increasing risk of global warming, hydrogen has been intensively investigated as a replacement fuel for the world. The fuel wold be very clean and very effective with numerous benefits but the main problem surrounding its use is the storage of such a potentially explosive material.

This investigation will look at Ammonia Borane, NH₃BH₃, a white, stable solid at room temperature with a high content of hygdrogen (~20% by weight). The formation of NH₃BH₃ is also relatively simple with an Ammonia salt and Borane salt being reacted in situ to produce NH₄BH₄. This is then reduced in organic solvent to the wanted Ammonia Borane product.

(Please note; Snapshots have been taken wherever possible to prove that the calculations have been run. For the final optimisation of the products the Gaussian Input File has been uploaded to wiki with the web link attatched.)

Results

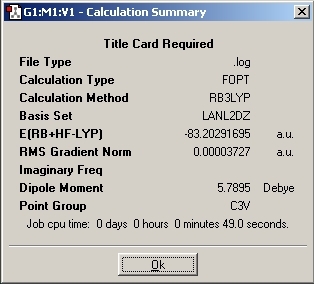
Ammonia Borane can exist in two conformations; eclipsed and staggered. Both of these were drawn in the Gaussview program with dihedral adjustments to create the eclipsed conformer. The B3LYP method with the LanL2MB basis set was first used as an optimisation. This method was chosen due to the simplicity of the calculations so that the calculation time was too long. Further adjustments could then be made to this optimised molecule which would greatly reduce calculation times.

B3LYP

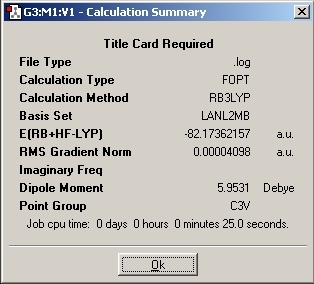
The first conformation analysed was the eclipsed conformation.

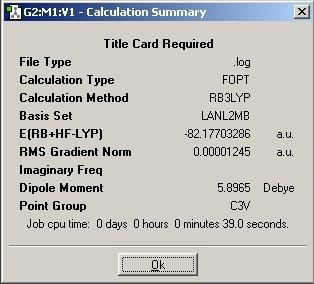
The bond was then rotated and the staggered conformation was analysed.

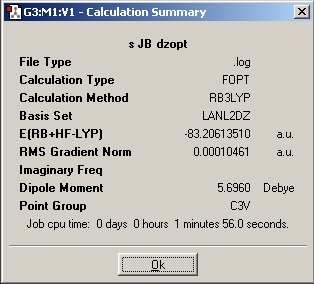
The method was then left unchanged but the basis set was increased to the more accurate LanL2DZ set.

Staggered Conformation

By changing the basis set, the energy has dropped by approximately 1 Hartree which is about 2500kJ/mol!!!

MP2

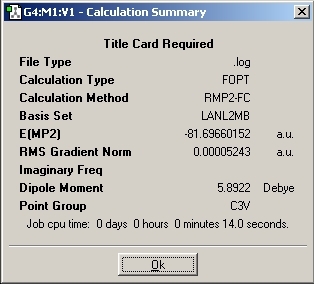
The relatively simple nature of Ammonia Borane due to all atoms being in the first row of elements meant that the MP2 calculation could be run with ease. The LanL2MB basis set was first used before the higher 6-311G(d,p) basis set was used. The MP2 calculations are a lot more accurate than the B3LYP which should make these set of results more reliable.

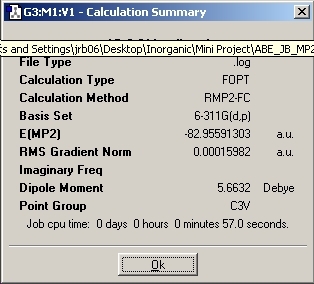
The energy of the eclipsed conformation was first investigated. Upon immediate observation of the results, it was clear that the energy of the molecule rose dramtically. It was therefore decided not to run the calculation for the staggered conformation to save time. The basis set was changed which should provide a better set of results. The 6-311G (d,p) basis set was used.

The file could not be uploaded to D-space so it was uploaded to wiki. There link is below: https://www.ch.ic.ac.uk/wiki/index.php/Image:ABe_JB_mp2611.gjf

The energy was again very different to the first MP2 calculation but a lot closer to the B3LYP method. It was therefore concluded that this basis set result is the most accurate obtained.

The staggered conformation was then run with this method and basis set:

https://www.ch.ic.ac.uk/wiki/index.php/Image:AB_JB_OPT_mp2611.gjf

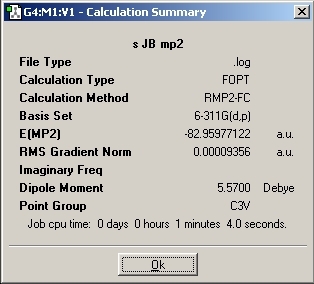
This method and basis set produced a very accurate and reliable set of results and so no further optimisation calculations were conducted. The two results were then analysed and the following conclusions were drawn:

By looking at the total energy of the molecule, it is possible to suggest that the Ammonia Borane molecule exists in the Staggered conformation. This conformation is 10.12kJ/mol +/- 1kJ/mol lower in energy than the eclipsed conformation. This can be further explained by looking at the distance between adjacent hydrogens. There is a difference of approximately 0.19Å +/- 0.01Å which helps explain why the staggered conformation is lower in energy. This is because the hydrogens are further away in the staggered conformation to the adjacent hydrogens which causes the electronic repulsions in the molecule to be reduced. The staggered conformation has lower steric hindrance and higher better stereoelectonic stabilisations so the energy is lower.

Using the Gaussian program, it is also possible to look at the difference in the N-B bond distance. The staggered N-B bond distance is 1.65Å +/- 0.01Å compared to 1.68Å +/- 0.01Å for the eclipsed conformation. As the staggered distance is shorter, this would suggest a stronger N-B bond. This means that the orbital overlap is better for the staggered conformation as there would be no hydrogen interactions.

Molecular Orbitals

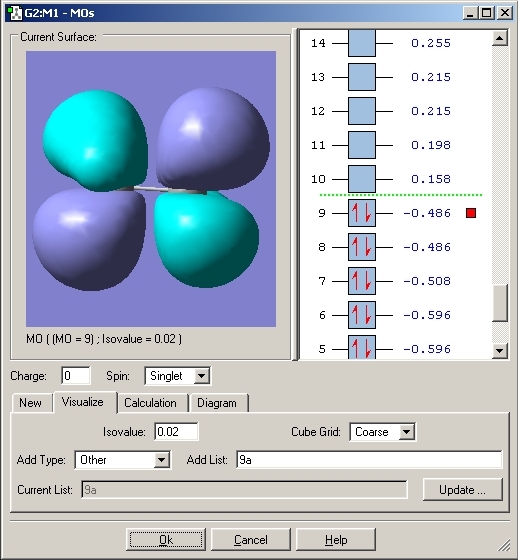
The molecular orbitals were then viewed using the checkpoint file and the Gaussian program. These would aid the explanation for the bonding in this compound. The HOMO orbital was analysed. The MO's for both Ammonia Borane and Ethane are included.

Eclipsed Ammonia Borane

Staggered Ammonia Borane

Eclipsed Ethane

Staggered Ethane

As can be seen with the MO's for Ammonia Borane, the overlap between the B and N orbitals is weak compared to that in Ethane.

The bonding between Boron and Nitrogen could have been explained by saying that the Nitrogen lone pair donates its electrons to the lewis acidic boron centre. This would create a dative covalent bond but looking at the MO's it is fair to say that a σ bond is created by overlap of the nitrogen lone pair and B-H σ^* orbital.

Comparison to Ethane

Ammonia Borane is very similar in size and isoelectronic nature to the widely used and studied organic molecule, Ethane. It would therefore make sense to compare the two compounds and their relative energies. The same method and basis set for Ethane must be used otherwise the comparison is invalid. The MP2 method with 6-311G (d,p) basis set was used to compare the energy difference between the staggered and eclipsed conformations.

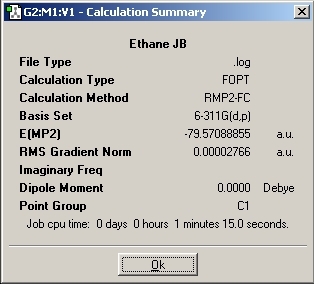
Staggered Results

D-space link unavailable so file uploaded here: https://www.ch.ic.ac.uk/wiki/index.php/Image:EthaneJB.gjf

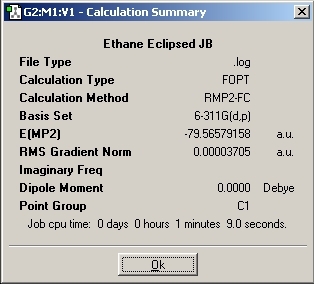
Eclipsed Results

D-space link unavailable so file uploaded here: https://www.ch.ic.ac.uk/wiki/index.php/Image:EthaneeJB.gjf

The total energies for both conformations was then analysed. The energy difference between the two was found to be 13.38kJ/mol +/- 1kJ/mol. This energy difference is higher compared to the Ammonia Borane molecule. This could be due to the fact that in ethane there would be better stereoelectronic overlaps causing a greater stabilisation. The overlaps would be better as the orbitals would all be the same size whereas in the Ammonia Borane there is orbital mismatch.

Products and Reactants

The reaction scheme given in the introduction was then used to calculate the relative energies for the products and reactants. The MP2 method was used along with the 6-311G (d,p) basis set.

Reactants

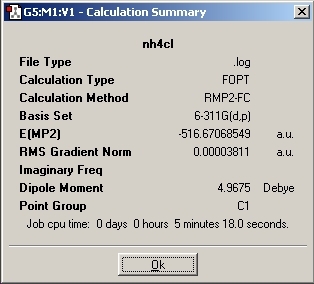
NH₄Cl

The NH₄ molecule was then drawn and the Cl was added at a distance of 3A from the hydrogens.

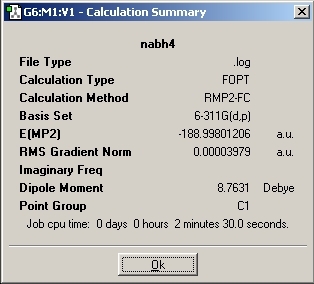
NaBH₄

https://www.ch.ic.ac.uk/wiki/index.php/Image:NABH44.gjf

Products

NH₄BH₄

The molecule was drawn in Gaussian and the H-H distance was set to 1.2A. initally the 3-21 basis set was used to reduce time and from the optimised structure the 6-311G basis set was used. The file has been uploaded to here: https://www.ch.ic.ac.uk/wiki/index.php/Image:NHBH1.gjf

NaCl

H₂

The energy of the reactants was found to be -705.666 and the products was found to be -705.58. Although these numbers are similar, they must be converted into kJ/mol before any reak analysis can be made. The energy difference was therefore found to be about -200kJ/mol. This shows that the products are more stable which would be expected as you are producing hydrogen gas (high entropy) and an ionic crystal salt, NaCl.

The intermediate product in the reaction, NH₄BH₄ was also optimised. The energy of this was approximately equal to the energy of NH₃BH₃ plus H₂ gas. The intermidate was slightly higher in energy making the formation of hydrogen gas and NH₃BH₃ favourable. This would be expected as the NH₄BH₄ does not contain a N-B bond. The final product, after the loss of hydrgoen gas which will entropically favour the reaction, is therefore lower in energy.

Question

Ammonia-Borane is isoelectronic with ethane. But whereas ethane has an extremely low melting point, the former melts aound 110^oC. Why?

At room temperature Ammonia-Borane is a solid molecular crystal with a melting point of 110^oC whereas ethane is a colourless gas. As the B-N bond has a change in dipole due to the difference in electronegavity of B (2.4) and N (3.4). This allows hydrogen bonding to form between two adjacent hydrogen atoms through a B-H--H-N bond. This causes the melting point of the structure to increase. This cannot occur in ethane as only carbon is present and so any dipole moments are cancelled.