Rep:Mod:jrb0614

Structure and Spectroscopy

Throughout this course, Molecular Mechanics (MM) will be used to gain an insight in the energies of different molecules. These mechanics are based on Newtonian Mechanics and they are used to model a system. However, inorder for these calculations to be possible, the modelling makes some key assumptions; Each atom is modelled as a single particle with a constant radius and net charge, and the bond length between two atoms is an equilibrium. The MM model calculates the stretching, bending, torsion and Van der Waals interactions between each atom and gives an estimate to the total energy of the molecule. As there are so many assumptions in the model, the results are used for comparison and not accurate energy calculations.

The Hydrogenation of Cyclopentadiene Dimer

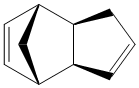
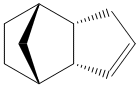
Cyclopentadiene dimers are formed via a Diels Alder reaction of two cyclopentadienes. One of the molecules acts as the dienophile and the other as the diene. Due to sterics, one of the molecules must attack from either above or below the other. This gives two isomers for the dimerisation product; exo (1) and endo (2).

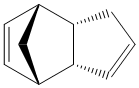
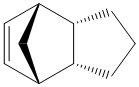
The hydrogenation of the dimer only occurs on the endo isomer and there are two possible positions of attack. The two products are shown (3) and (4).

Exo Dimer (1)	Endo Dimer (2)	Hydrogenated Endo Product (3)	Hydrogenated Endo Product (4)

The geometry of the dimers can be optimised and analysis can be carried out to determine the energy contributions to the total energy. The results can then be used to determine whether the dimerisation gives the kinetically or thermodynamically favoured product.

Energies (kcal/mol)	Exo Dimer (1)	Endo Dimer (2)	Hydrogenated Endo Dimer (3)	Hydrogenated Endo Dimer (4)
Stretch	1.2735	1.24540	1.2244	1.09580
Bend	20.5652	20.8603	18.8500	14.5087
Stretch-Bend	-0.8366	-0.8320	-0.7530	-0.5501
Torsion	7.6617	9.5039	12.2374	12.4979
Non 1,4 VdW	-1.4017	-1.5083	-1.5459	-1.0521
1,4 VdW	4.2395	4.3012	5.7556	4.5129
Dipole-Dipole	0.3777	0.4448	0.1631	0.1407
TOTAL	31.8794	34.0153	35.9317	31.1537

From the analysis above, it can be seen that the exo isomer is the most thermodynamically stable as it has the lower total energy. It would therefore be expected to be the major product but in fact the endo isomer is the major product. This would suggest that the endo isomer is the kinetically favoured and that the reaction is kinetically controlled. The endo intermediate is formed at a lower energy than the exo intermediate.

The hydrogenated reaction only works for the endo products. The hydrogenation can occur at 2 different positions and the two different products are shown (3) and (4). This reaction is thermodynamically controlled and the thermodynamic product, product 4 has the lowest energy.

By considering the calculation results, it is possible to suggest that the bending strain is lower in product 4 compared to product 3. The double bond in product 4 is under less strain. The hydrogenation reaction is thermodynamically controlled and so the most stable, lowest energy product predominates.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring

Alkylation of Prolinol

Molecular calculations can be used to explain the stereochemistry of the reactant and the subsequent product as shown in figures 5 and 6.

The starting position of the carbonyl was changed until the lowest energy geometry was achieved.

A Grignard reagent, methyl magnesium iodide, was then used to alkylate the pyridine ring with the position of attack being C4. The stereochemistry of the product 6 can then be explained using the molecular calculations.

Reactant (5)	Product (6)

Energies (kcal/mol)	Reactant (5)	Product (6)
Stretch	0.8863	1.0490
Bend	6.4691	9.1135
Stretch-Bend	0.1115	0.2072
Torsion	9.8048	11.4205
Non 1,4 VdW	-2.6927	-2.4311
1,4 VdW	11.4799	12.9545
Charge-Dipole	3.2556	----
Dipole-Dipole	-3.7702	-3.8816
Dihedral Angle	41	37
TOTAL	25.5442	28.4322

The carbonyl is not co-planar with the aromatic ring system and so a dihedral angle of 41^o is observed compared to an angle of 0^o if the carbonyl was planar.

The product is higher in energy than the reactant due to the loss of aromaticity in the pyridine ring.

Mechanism of Reaction

Methyl magnesium iodine attacks the C4 position of the ring as a methyl carbanion and magnesium iodide cation. The magnesium chelates to the carboxyl oxygen and causes the methyl to attack on the top face if the ring, giving the stereochemistry shown. A magnesium enolate is generated when the methyl ligand from magnesium through conjugate delivery to the carbon.

Nucleophilic Addition of NHPh

The MM2 calculation to minimise the energy was again run for the molecules shown (7). The starting position angle of the carbonyl was again changed until the lowest possible energy conformation was achieved.

Reactant (7)	Product (8)

Energies (kcal/mol)	Reactant (7.1)	Reactant (7.2)
Stretch	1.5467	1.6139
Bend	6.7007	6.7475
Stretch-Bend	0.3311	0.3397
Torsion	-6.4930	-6.5193
Non 1,4 VdW	-1.7051	-1.7617
1,4 VdW	17.6082	17.5872
Charge-Dipole	2.4099	2.3750
Dipole-Dipole	-4.7962	-4.7991
Dihedral Angle	-41	-43
TOTAL	15.6023	15.5832

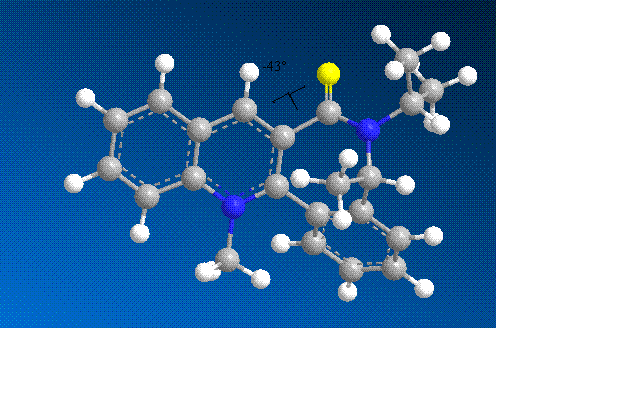
The energy was minimised and dihedral angles of -41^o and -43^o were seen, with the dihedral angle of -43^o having the lowest energy conformation. The negative angle shows that the C=O is below the plane of the aromatic ring. Inoder to achieve this the 7 membered ring was inverted but the stereochemistry of the methyl was retained. The screenshot below shows the dihedral angle:

The PhNH₂ attacks the aromatic ring, stablising the positive charge on the nitrogen although aromaticity is lost. The attack has the same stereochemistry as the Grignard attack but for different reasons. PhNH₂ does not have the ability to coordinate to the carbonyl and compared to the Grignard it is a lot more sterically hindered. The stereochemistry is therefore controlled by sterics.

By analysing the model results, the lowest energy and therefore most stable conformation is when the PhNH₂ attacks from the top of the ring due to there being less steric hindrance as the caronbyl is below the ring.

Improvements

Improvements can be made to the model so that a more accurate explanation for Nucleophilic and electrophilic attack can be made. More parameters need to be included in the calculations so that a better understanding can be achieved.

The activation barriers and transition state energies would also give a much more information about the mechanism of reaction and would allow for thermodynamic and kinetic analysis.

The MM2 model is based on Newtonian mechanics which creates a very quick and powerful program for comparing stereochemistry but not a detailed understanding of the stereochemistry. Electronic calculations for the molecules would be required to explain the positions of Nucleophilic and electrophilic attack.

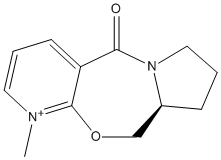
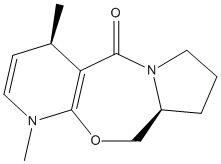
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

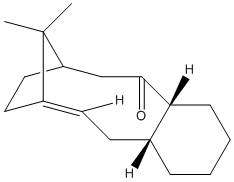
This part of the investigation involves the molecule Taxol which is an important drug used for the treatment of ovarian cancer. The carbonyl group can be pointing either up or down as proposed by Paquette.

The carbonyl in this molecule has the ability to switch from up to down and vice versa. This type of isomerisation is known as atropisomerism.

Intermediate (10)	Intermediate (11)

Energies (kcal/mol)	Intermediate (10)	Intermediate (11)
Stretch	2.6979	2.5742
Bend	15.8394	11.4137
Stretch-Bend	0.3998	0.3481
Torsion	18.1548	18.7389
Non 1,4 VdW	-0.9893	-1.3081
1,4 VdW	12.6323	12.9812
Dipole-Dipole	0.1491	-0.1775
TOTAL	48.8841	45.0183

From the above molecular calculations it can be seen that when the carbonyl is pointing down (Intermediate 11), the lowest energy is achieved. The first calculations gave the molecule in the boat conformation. An initial energy of about 51 kcal/mol was achieved for intermediate 11 so the cyclohexane ring had to be manually changed to create the chair (favoured) conformation. This substantially lowered the energy of the molecule and with some more minor adjustments, the energy was lowered to 45.0 kcal/mol. The same problem occurred with intermediate 10 and again the energy was lowered by manually creating the chair conformation as seen in the image below.

Comparing the two isomers it can be seen that there is only a small energy difference (~3.8 kcal/mol) between the two which suggests that there is isomerisation between the two forms. Intermediate 11 is more stable as the carbonyl is pointing down into the molecule. This creates a cage around the structure of the olefin and due to the large size, intermediate 11 is more stabilised as it is a hyperstable olefin.

Peptide

This experiment investigates a peptide and the effect that isomerisation has on the rate of hydrolysis. The two isomers are very simalar with one being of cis and one of trans conformation. The stereochemistry for the moelecule was given, but the peptide chain wasn't resulting in 4 possible conformations for the molecule.

Cis Isomer (13)

Axial 13	Equitorial 13
Axail (13)	Axail (13)

Energies (kcal/mol)	Axial 13	Equitorial 13
Stretch	1.4309	1.6128
Bend	7.8174	5.7837
Stretch-Bend	0.5943	0.5857
Torsion	11.6495	8.5832
Non 1,4 VdW	-8.2087	-5.6729
1,4 VdW	10.5017	9.4627
Dipole-Dipole	-4.4963	-6.5562
TOTAL	19.2889	13.7990

This molecule is based on the cis-decalin ring system and the peptide can either be equatorial or axial. The first conformation analysed was the axial peptide position and the hydroxyl group on the equatorial position. An initial energy of 177 kcal/mol was achieved but the hydroxyl group was moved to the equatorial position so that the stereochemistry was the same as that shown in the diagram. The energy was dramatically reduced to approximately 20 kcal/mol. Upon further rotations of the peptide chain, the lowest energy of 19.2889 kcal/mol was achieved when the C=O bond faced the hydroxyl group. The peptide chain was then changed to the equatorial position and a lower energy conformation of 13.7990 kcal/mol was achieved after several modifications. From the above calculations is can be seen that the thermodynamically favoured conformation is when the peptide chain and the hydroxyl group are equatorial. This difference in energy is due to hydrogen bonding between the carbonyl and hydroxyl groups. H-bonding considerably lowers the energy of the molecule as it greatly reduces the dipole-dipole interaction.

Trans Isomer (14)

Axial 14	Equitorial 14
Axail (13)	Axail (13)

Energies (kcal/mol)	Axial 14	Equitorial 14
Stretch	1.5235	1.5390
Bend	5.1371	3.2732
Stretch-Bend	0.5507	0.4916
Torsion	8.6972	7.4165
Non 1,4 VdW	-6.9614	-8.2358
1,4 VdW	9.6105	9.8769
Dipole-Dipole	-6.5271	-5.2925
TOTAL	12.0305	9.0688

The trans isomer cannot undergo ring flipping and so the hydroxyl position is locked. Again the axial position was investigated first and the initial energy was high. As with the cis isomer, the peptide was rotated until the lowest possible energy was achieved. An energy of 12.0305 kcal/mol was achieved.

The equatorial position was then analysed and the energy was considerable lower, with an energy of 9.0688 kcal/mol achieved. The energy was lower due as the hydrogen bonding was stronger as the two groups were closer.

Discussion

The reaction is a Nucleophilic attack with the hydroxyl oxygen attacking the carbonyl double bond. The lone pair of the hydroxyl attacks the π*C=O, which is at an angle of 107^o. This angle was first investigated by Burgi and Dunitz and became known as the Burgi-Dunitz angle. The closer the angle of attack to 109^o, the faster the reaction due to stereoelectronic arguments.

Modelling Using Semi-empirical Molecular Orbital Theory

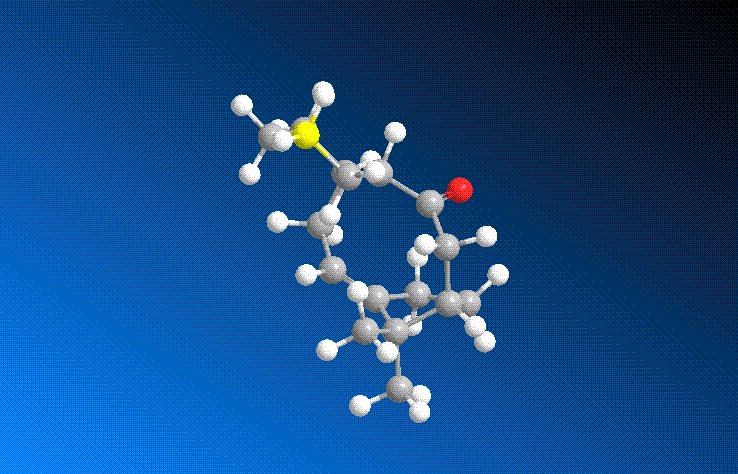
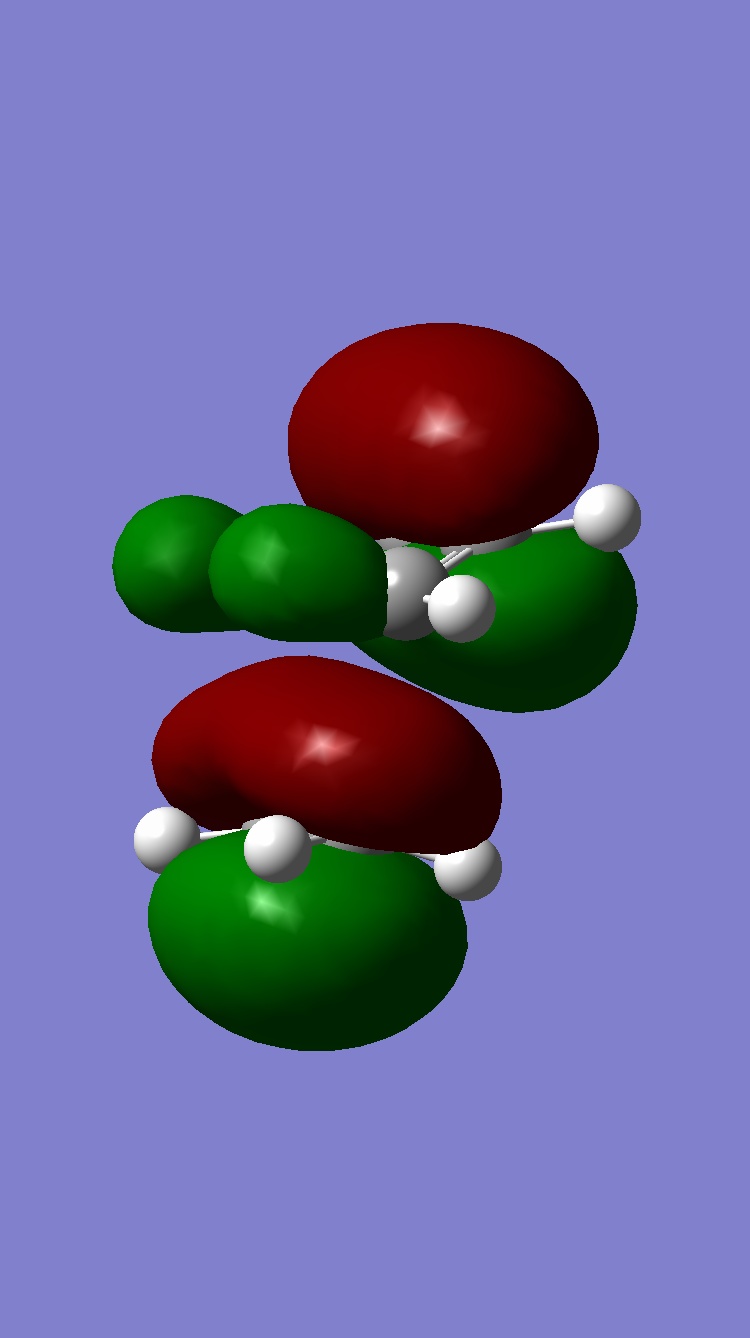
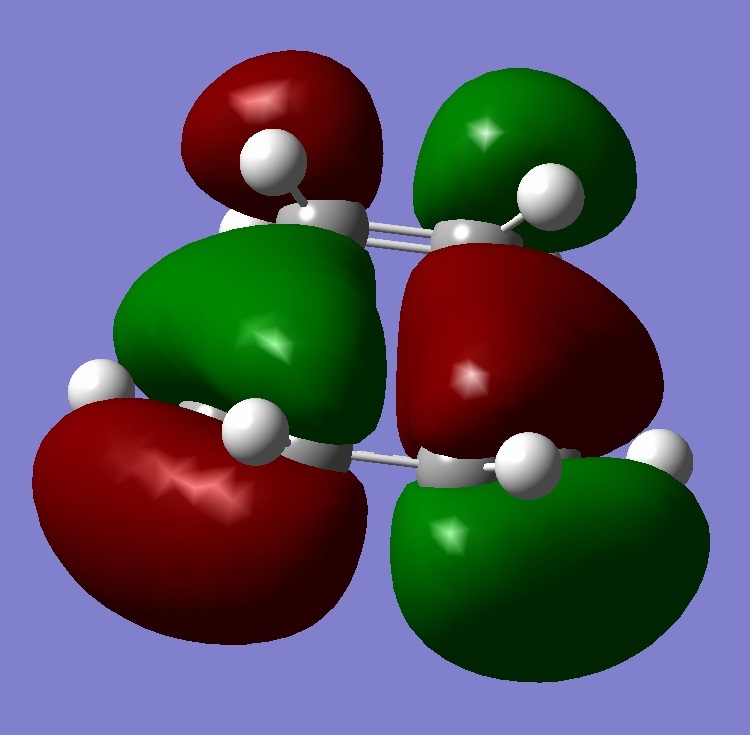
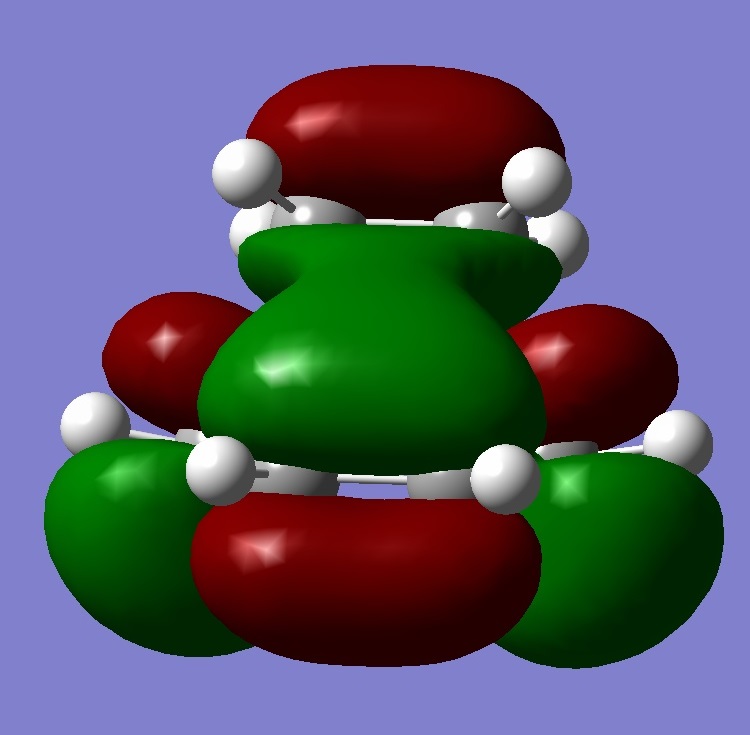
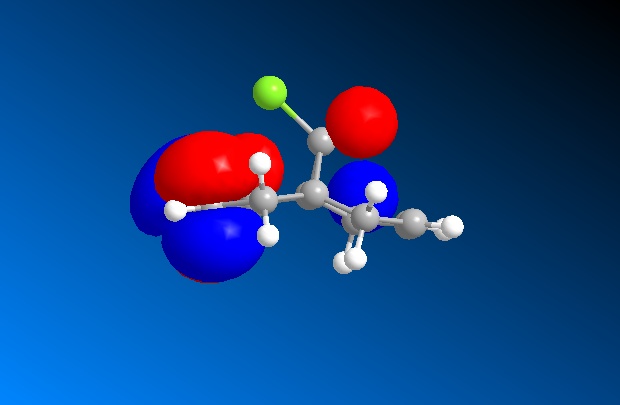
This part of the investigation uses semi-empirical molecular orbital theory to explain the regioselectivity of the following molecule. This calculation method is more advanced than the basic molecular modelling calculations previously used and calculates the molecular orbitals of the molecule from the atomic orbitals. The energy of the molecule is calculated using a self-consistent-field molecular orbital method and from this calculation, graphical representations of the molecular orbitals can be shown. The calculations and diagrams should help to explain why the exo double bond to the chlorine is hydrogenated and not the endo.

The molecule was first optimised using the MM2 method and a minimum energy of 17.8982 kcal/mol was achieved. This file was then saved and uploaded into Gaussview and the B3LYP/ 6-31G method was sent to the Chemistry SCAN system to be calculated. The file was then downloaded and opened with Gaussview. The method ran was the Density Function Theory (DFT) and from this the molecular orbitals of the molecule as well as the vibrations can be seen.

HOMO	HOMO-1

LUMO	LUMO+1

LUMO+2

The regioselectivity of this reaction can be explained by looking at the HOMO-1 and LUMO+2 MO’s. Looking at the LUMO+2 MO, it is clear to see that there is a favourable antiperiplanar relationship between the C-Cl σ* and exo double bond π orbital in the HOMO-1. This allows electron density to pass from the alkene bond to the C-Cl σ* which causes the π bond to be less nucleophilic.

Looking at the bridgehead carbon and the exo / endo distances, the two distances for exo can be explained by distortion of the molecular orbital overlap.

As the electron density is donated into the C-Cl σ* bond, this destabilises the C-Cl bond and makes the bond longer. Looking at the equation: v = 1/2π (k/μ) ½ the effect this destabilisation has can be analysed using IR. As k is the force constant of the bond, when the bond strength is weakened, the frequency is lowered. Thus, when the diene is hydrogenated, the exo π bond is no longer present and so the C-Cl σ* bond is not destabilised. This leaves the hydrogenated C-Cl bond to have a stretching frequency of about 4cm-1 stronger than the diene.

Stretch	Diene (cm-1)	Hydrogenated alkene (cm-1)
C-Cl	772.613	776.83
Exo C=C	1740.79	-
Endo C=C	1760.98	1761.66

Mini Project - Click Chemistry

Introduction

Click Chemistry is a powerful branch of organic chemistry as it allows small molecule units to join together quickly with high stereospecificity with the aid of a metal catalyst. These properties have allowed the click reaction to become a very useful synthesis tool in material science and biology. The example investigated here is the 1,3-dipolar cycloaddition between an azide and an alkyne to give a 1,2,3-triazole. The reaction is can form two isomers, A and B, which can be controlled using metal catalysis. The 1,4 isomer (A), is formed when a Copper (I) catalyst is used and the 1,5-isomer when a Ru(II) catalyst is used.

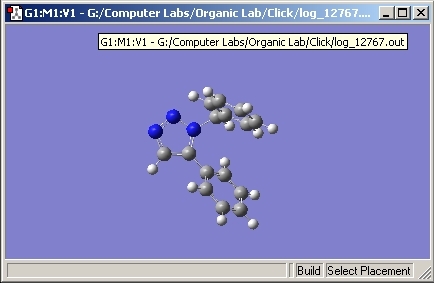
In order to explain the regioisomers, the most effective spectroscopic method would be ¹³C NMR. The isomers were first drawn and optimised in ChemBio 3D using the basic MM2 calculations. These are not powerful enough and so the molecules were uploaded to the Gaussian program where a more detailed calculation could be run. A 6-31G(d,p) basis set optimisation was run on the two isomers. Due to the complex size of the isomers, the files were sent to Chemistry SCAN. The optimised geometries were then resubmitted to SCAN to calculate the ¹³C NMR for each one. The results were then opened and the NMR spectra were compared to literature.

Results

Geometry of A

Geometry of B

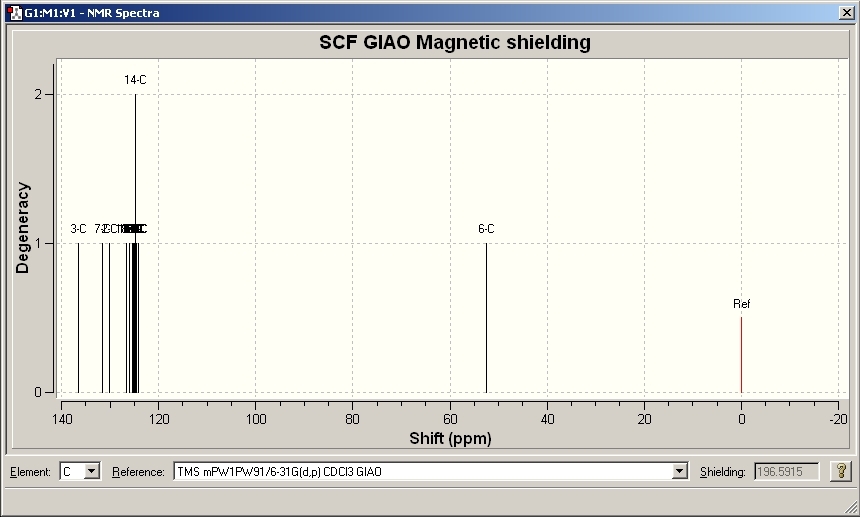
NMR Results for A

Model Chemical Shift ppm	Literature Chemical Shift ppm
54.744	54.0
117.661	119.5
121.209	125.5
124.284	127.9
124.993, 125.204	128.56
125.94	128.9
127.359	130.4
132.562	134.6
144.862	148.0

NMR Results for B

Model Chemical Shift ppm	Literature Chemical Shift ppm
52.122	51.85
124.135	126.93
124.492	127.22
125.207, 125.320	128.22
125.471	128.92
125.961	129.08
126.087	129.64
126.644, 126.678	133.26
130.225	133.34
131.621	135.66
136.526	138.26

Discussion

Comparing the spectra for isomer A to literature, it is fair to say that the molecular calculations are a very good estimate to the real data. . The shift of the peaks is slightly different but this is to be expected as the molecular calculations contain assumptions. Isomer B also shows very good correlation to literature.

Comparing the two spectra, they are very similar with the exception of one peak. Isomer A contains a peak at approximate 148ppm whereas Isomer B doesn’t. This is due to the chemical environment of the carbon. In Isomer B, the peak appears at approximately 133ppm. The geometry of isomer A allows both the nitrogen and phenyl aromatic systems to be in the same plane. This causes a delocalised conjugated system through the molecule and causes the carbon to be very deshielded, increasing the chemical shift. However, in isomer B, the planar system is impossible to achieve due to the steric bulk of the phenyl groups. The phenyl groups cannot be arranged in a way to create a planar system and so the conjugation is lost, hence a lower chemical shift is seen. The vibrations of the isomers were also looked at and the IR spectrums were produced. Due to the very similar nature of the molecules and the fact that the vibrations are basically the same, the spectra were very similar and are not useful for this explanation. In conclusion, molecular modelling can be used as a very powerful and accurate method to predict the geometry and spectra of molecules. As with all calculations, assumptions are made throughout the calculations and this explains why the peaks do not perfectly match the experimental. The modelling also gave many more peaks compared to the experimental due to there being a very high resolution.