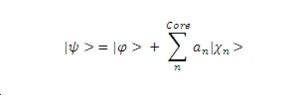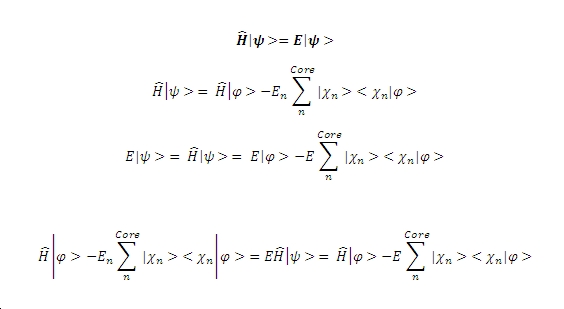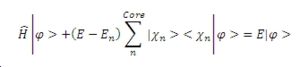Rep:Mod:jp806inorganicrewrite1

Module 2: Inorganic

Part 1: Experiments in Inorganic CompChem

The BH₃ Molecule

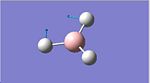
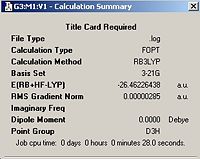
A molecule of BH₃ was defined using GaussView and then manipulated to give all bond lengths of 1.5 Å. The molecule was then optimised using the B3LYP method and the 3-21G basis set . The optimised molecule had equal bond lengths of 1.19435Å and equal bond angles of 120.00^o. The output file for this optimisation can be seen below along with a screen shot of the output summary.

BH3
Optimised Gaussian Output	Calculation Summary
Cyclopentadiene Endo Dimer

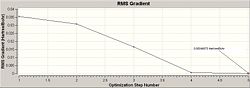
The optimisation of the BH₃ was then analysed by opening the .log file with the "Read Intermediate Geometries" option checked. The table below shows the plot of total energy and energy gradient against optimisation step number as well as a visual representation of the molecule at each point in the optimisation.

Analysis of Optimisation
Optimisation Point	Total Energy Profile	RMS Gradient	Molecular Representation
1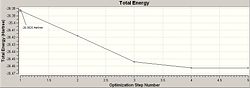
2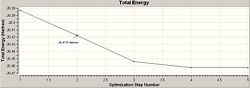
3
4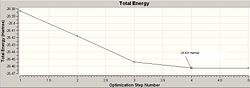
5

Aside 1: The Meaning of Optimisation in Gaussian

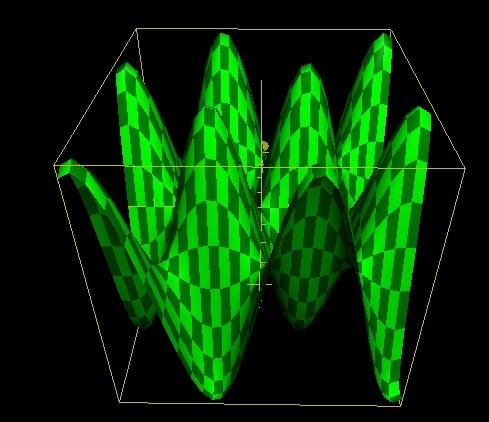
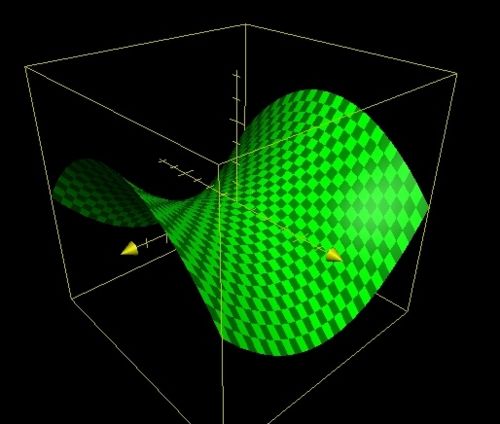
In order to optimise the molecular structure of the input a potential energy surface (PES) is used, this usually involves two degrees of molecular freedom and forms a surface by plotting the energy above the plane. The height of a structure on the surface is equal to that particular conformations energy. In general there are three types of stationery points one must consider when evaluating a PES these are: 1. Maxima these represent areas of maximum energy and are found by calculus since f'(x,y)=0 and f"(x,y)<0 at maxima. 2. Minima these represent areas of minimum energy and are also found by calculus since f'(x,y)=0 and f"(x,y)>0 at minima. 3. Saddle Points are the three dimensional equivalent of a 2D point of a inflection defined by f'(x,y)=0 and f"(x,y)=0.

Examples of Stationery Points
Maxima/Minima	Saddle Point
f(x,y)=10sin(x/2)sin(y/2)	f(x,y)=x2-y2

Examples of all 3 stationery points can be found above, these were plotted using the functions given in the table on the 2005 Apple Computer Inc Grapher (version 1.1) software. There are then two types of extrema local and global. A local point represents a stationery point that is the extrema for a particular region of the PES. A global extrema represents an extrema for the entire surface. In an optimisation program the algorithum used seeks to find a stationery point, this stationery point is hopefully the global minima it is however possible for the algorithum to get stuck in a local minima and therefore return an optimised structure that is not of the lowest possible energy. In an attempt to prevent the optimisation from becoming stuck in a local minima Gaussian has 4 criteria that must be satisfied for optimisation to converge, these are listed below.

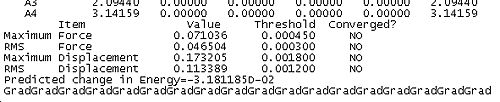
The forces must be less than 0.00045 this is effectively saying that the forces must be 0. Forces are critical since force is the negative differential of potential (F=f'(V)) hence at an extrema the force will equal zero since the differential of potential equals 0.

The root mean square of force must be below 0.0003. A root mean square force esentially gives a statistical measure of the size of the force.

The calculated displacement of the subsequent step must be less than 0.0018. That is the distortion to the molecular geometry must be very small for the next step

The root mean square of displacement must be less than 0.0012

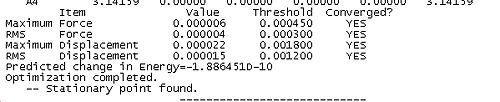
Together these criteria serve to reduce the likelihood of Gaussian predicting a minimum to early in a calculation. Reading the output from an optimisation can yield some useful and interesting data as well as demonstrating the application of the above criteria for convergence in the algorithum. In the case of BH₃ the convergence was achieved in 5 steps. The table below shows snapshots of the first and last step in the convergence, note that the energy of the final molecule is calculated and printed in the penultimate step of the optimisation.

Optimisation Output
Step 1	Final Step

Immediately after the convergence criteria are satisfied the final molecular structure is printed, this also prints the optimised molecular parameters of bond length, bond angle and dihedral angle. In the case of BH₃ the angles and bond lengths changed thus:

Optimisation Output
	Input (Initial)	Ouput (Converged)
Bond Angle	120.0o	120.0o
Bond Length	1.5 Å	1.1944 Å
Dihedral Angle	180.0o	180.0o

From this data it is clear that the bond and dihedral angle remained constant whilst the bond lengths decreased by 25% relative to the original bond length.

BCl₃

A pseduopotential is used in this section, a pseduo potential removes the complicated effects of a systems core electrons. When a valence electron wavefunction passes through the core it oscillates rapidly to maintatin orthogonality with the tightly bound core electrons. So in this approximation the core electrons are considered to have a pseudo-potential that then acts on the valence electrons pseudo-wavefunction. This pseudo-potential is designed to remove the rapid oscillations in the core region instead replacing it with a smooth more mathematically simplistic pseduo-wavefunction. Outside of the core region hte pseudo wave function behaves exactly as the valence electron wave function. Chemical physics demonstrates that the core electrons have little effect on the reactivity and properties of a species and thus the simplification is valued. A more mathematical treatment can be seen below:

(ITAL) Justification 1:

Following the mathematics presented by clearly demonstrates that the pseduo-wave function is of the same energy as valence electron wave function. Unfortunately the mathematics editing facility on the wiki is currently not functioning so instead equations have been saved and inserted as image files. First one must consider what it is we want a pseudopotential to do. We want it to model in a smooth manner the with the wave function for a valence electron, so consider the wave function defined below with a constant term added for the core electrons states.

As has already been mentioned the valence electron wave function must be orthogonal to the core electron wave function, this allows us to determine a substitution for the value of a_n. Substituting this into the equation defined in part 1 gives a new version of the same wave function.

If the Schrodinger equation is then considered along with the fact that we assign an energy Eigenvalue of E_n the following result comes from the substitution and rearrangement:

From the equation it is clear that two operators now exist, one is the Hamiltonian whilst the other is an operator for the potential energy of the nucleus, condensing the equation into operator form therefore gives the following results.

The final equation then shows how the energy of the smooth function (pseudo-wavefunction) that includes a term for pseudo-potential is of the form as the valence electron wave function. This means that the method of pseudopotentials is valid.

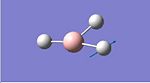
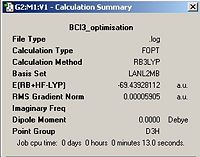
A molecule of BCl₃ was first defined in GaussView and a Density Functional Theory (DFT), the B3LYP was again employed using the Lanl2mb option that implements the basis set D95V for first row elements and the Los Almos ECP on heavier elements . After optimisation the bond lengths were constant throughout the molecule at 1.86592 Å the bond angles were also constant at 120.00^o. The optimised molecule and calculation summary can be found below.

BCl3
Optimised Molecule	Calculation Summary
Cyclopentadiene Endo Dimer

Own Small Molecule: PCl₃

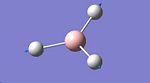
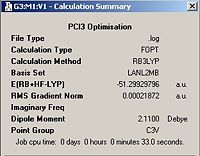
A molecule of PCl₃ was first defined using GaussView this molecule was then optimised using DFT/B3LYP with the LANL2MB basis set. The optimised molecule can be seen below, unfortunately the optimal structure was such that the phohphorus and chlorine atoms were not sufficiently close to be defined as bonded by Gaussian. The optimised structure could not be uploaded into D-Space and can be found on the CD provided as pcl3.log. The structure can also be found below along with the calculation summary from the Gaussian Job.

PCl3
Optimised Molecule	Calculation Summary
Cyclopentadiene Endo Dimer

According to these calculations the PCl₃ molecule has a C_3V point group whereae the BCl₃ has a D_3h point group. This is due to the trigonal pyrimadal shape adopted by PCl₃ in comparisson to the trigonal planar shape adopted by BCl₃. This is due to the presence of a lone pair on the P that the B atom does not have. In this case the cartesian co-ordinates are shown below:

Coordinates of Atoms
Atom	Position (x,y,Z)/Å
P	(-0.031876, 0.055211,-0.022540)
Cl(1)	(-0.001189, 0.002059, 2.160126)
Cl(2)	(2.036190, 0.002059, -0.721163)
Cl(3)	(-1.019878, -1.762363, -0.721162)

The bond lengths in the optimised molecule were all equal at 2.39746 Å and the Cl-P-Cl bond angle is 99.51414^o. This bond angle is close to the 103.6^o bond angle expected for this compound . The bond length of 239pm is however substainally different from the expected bond length of 204pm

Further Work on BH₃

The optimised BH₃ molecule from section 1.1.1 was taken and a frequency calculation was run, the calculation was run as a DFT B3LYP with a basis set of 321-1G the geom=connectivity and pop=full options were also implimented. The energy after the optimisation was given as -26.46226438 a.u after the frequency calculations were conducted the summary pane gave the energy as -26.46226438 a.u. this demonstrates that the frequencies have been calculated for the molecule that was optimised. Gaussian calculated 6 possible modes of vibration for the molecule and these can be seen in the table below. (nb. Vibrations occur in forward and back directions along the displacement vectors)

Vibrational Modes of BH3
Number	Diagran	Description	Frequency/cm-1	Intensity	Symmetry of D3h
1		H remain fixed B moves back and forth through plane of H atoms	1145.71	92.6991	A"
2		One H remains fixed other H atoms scissor around vibrating boron.	1204.66	12.3789	E'
3		Boron fixed all three H atoms transverse Boron atom.	1204.66	12.3814	E'
4		B fixed H atoms radiate from center moving in and out.	2592.79	0	A'
5		1 H atom fixed other two moving into and away from vibrating Boron.	2731.31	103.837	E'
6		Boron fixed H move towards and away from.	2731.31	103.83	E'

The point groups were derived using character tables available at http://www.webqc.org/symmetry.php. The character tables were applied to the determine the group with the vibrations being dealt with as static objects. The spectrum option was used on the vibrations pane in order to produce a computed IR spectrum for BH₃, this spectrum can be seen below and has only 3 peaks. This is not immediately obvious since the frequency calculation returned 6 possible vibrational modes and each vibrational mode represents a possible peak on an IR spectrum. In this case however four of the possible vibrational modes are degenerate (2 pairs of degenerate vibrations) and one vibrational mode at 2592.79cm^-1 has a zero intensity, therefore one would expect 3 peaks in the IR spectrum as is observed.

Predicted IR-Spectrum for BH3

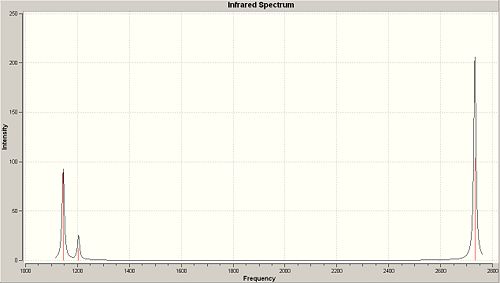
The qualitative molecular orbital diagram of BH₂ was drawn and can be seen below. The qualitative orbitals were compared with those generated on GaussView this comparisson can be seen in the table immediately below the MO diagran. The MO were generated quantitatively by setting the pop=full option in a calculation pane for the optimised BH₃ molecule, the result of this calculation was then viewed as a check point (.chk) file in the MO visualisation tool found under the Edit menu.

Qualitative MO for BH3

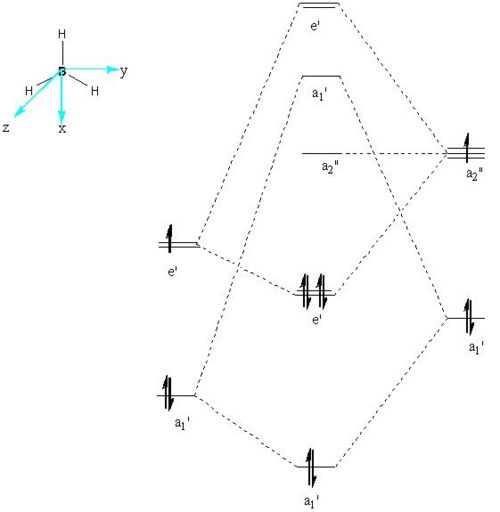
MO Comparisson for BH3
Molecular Orbital	Symmetry	Qualititative	Quantitative	Comments
1	a1'			Very similar with little difference between qualitative and quantitative shape. Overall shape could be easilt predicted qualitatively
2	e'		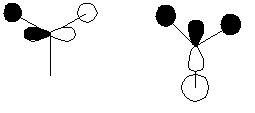	Closer to second qualitative MO but again both qualitative and quantitative in good agreement.
3	a2"			Very similar but difference in shape of lobes not predicted quantitatively.
4	a1'			Similar to qualitative with alrge lobes centred on the B atom disguing the H atoms.
5	e'	File:Jp806qualmo5.jpg		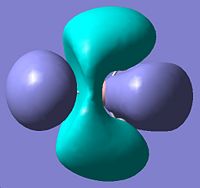blah

The quantitative process generated an MO for the 1s electrons in boron, these core electrons are not involved in bonding and were therefore excluded from the qualitative MO diagram. The MO orbital and qualitative prediction for this orbital can be seen below.

MO Comparisson for BH3 2
Molecular Orbital	Symmetry	Qualititative	Quantitative	Comments
1	a1'			This is almost an exact match between qualitative and quantitative MOs.

This work suggests that qualitative MO theory is of a reasonable level of accuracy since all the MO orbitals generated by Gaussian were very similar to the qualitative MOs created. A key difference is that the quantitative MO calculations give the exact shapes of the MOs which cannot be easily predicted qualitatively. Furthermore quantitative MO calculations give accurate relative energies for each MO, these energies lead to more accurate MO diagrams than those predicted qualitatively.

The Ammonia Molecule

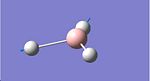
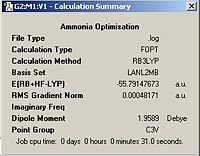
An ammonia (NH₃) molecule was defined on GaussView and then minimised using the B3LYP method and the 6-31G basis set, the optimised molecule and calculation summary can be found below.

Ammonia Optimisation
Ammonia	Calculation Summary
Cyclopentadiene Endo Dimer

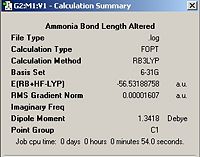
A second molecule of ammonia was then defined and a bond length changed to 1.01 Å from 1.00Å, all other bond lengths were kept as pre-defined by Gaussian. The molecule was the optimised using the B3LYP method and the 6-21G basis set with the ignore symmetry option selected. The result of this calculation can be found below.

Ammonia Altered Bond Length Optimisation
Ammonia (1.01 Å)	Calculation Summary
Cyclopentadiene Endo Dimer

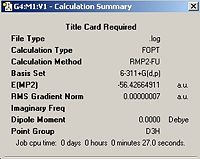
A high symmetry molecule of ammonia was then downloaded from http://www.ch.ic.ac.uk/hunt/teaching/teaching_comp_lab_year3/9b_nh3_symmetry.html this file was first converted to a Gaussian input file by changing the extension from .txt to .gjf. This was then minimised using a MP2 with a 6-311G basis set, the output file and summary can be seen in the boxes below.

Ammonia With a Dummy Atom
Ammonia (Dummy Atom)	Calculation Summary
Cyclopentadiene Endo Dimer

The symmetry of the input file has made a difference to the final structure in the C_3v case the molecule is trigonal pyrimidal this is also true in the C₁ case, however in the C₁ case the difference between the N centroid and the H plane is less than in the C_3v case. The D_3h case which is of highest symmetry has a planar structure. The symmetry also hasa marked effect on the calculation time, the higher the symmetry of the molecule the faster the calculation runs, for example D_3h runs in 27s whereas C₁ takes twice as along at 54s. The symmetry of a molecule can be broken if the ignore symmetry tab is checked. However under normal circumstances the Gaussian Program will always attempt to optimise the molecule within its point group. This means that by inputing a highly symmetrical molecule the computational expense of calculation is reduced since there are fewer possible alterations to the molecule. The higher the symmetry of the input the higher the energy of the output in this case D_3h is of the highest energy. The energy difference between the isomers of lower symmetry is ΔE=1.2 kJmol^-1. This is a very small energy and therefore is of limited significance.

Symmetry

In this discussion of ammonia three different point groups have been assigned these are C₁, D_3h and C_3v. Point groups are derived from group theory, in this case C₁ is a subgroup of C_3v whic is in itself a subgroup of D_3h. A subgroup is defined thus "A subset H of a group G is a subgroup of G if H is itself a group with respect to the operation on G". A proof of this could be attempted by first showing that the sub group C_3v is a closed group (complete) and then that each operation is an operation of D_3h. Unfortunately due to time and a lack of insight on my part this proof could not be elegantly completed.

MP2 (Moller-Plesset Perturbation Theory (see end) is a higher level of calculation and this was the carried out on the C_3v and D_3h ammonia molecule. The results of this optimisation can be seen in the table below.

Ammonia Via MP2
Ammonia C3v	Calculation Summary	Ammonia D3h	Calculation Summary
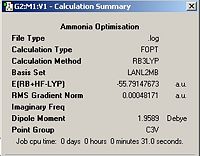
Cyclopentadiene Endo Dimer		Cyclopentadiene Endo Dimer	File:Jp806ammoniamp2hssummary.jpg

Surprisingly these calculations took less time to compute than the lower level calculations. From the calculations the barrier to the inversion can be calculated by finding the difference between the energies of the two symmetries. In the case of MP2 this was found to be ΔE=31.2 kJmol^-1 this is reasonably close to the experimentally determined value of 24.3kJmol^-1. Under the lower level conditions a value for ΔE=43.9 kJmol^-1 was found this is clearly very different from higher level calculation and of lower accuracy (less correlation with experiment). This barrier represents the benergy barrier through which the ammonia protons must tunnel. This quantum tunnelling requires a change to the Schrodinger wave equation in which the nuclei can no longer be modelled as harmonic oscillators but rather as wave. This means a nuclear wave function must be included in the Schrodinger equation.

The Inversion Mechanism

There are two basic mechanisms that one could propose for the inversion of ammonia. The first mechanism involes the movement of the N atom from the equilibrium position. In this model the potential energy surface is plotted as energy against reaction coordinate where reaction coordinate is effectively the distance between the N atom and the plane of the three H atoms. In modelling this mechanism the NH bond length is kept constant, this means that the NH bonds will move into space and the HNH bond angle will be altered between the two C_3v species this renders this mechanism physically unrealistic. The diagram below demonstrates this mechanism for inversion.

Ammonia Inversion Mechanism 1

Inversion Mechanism 1

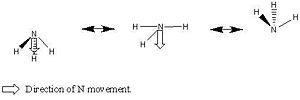
Another proposal is that the inversion is caused by the movement of the H atoms about the N centre, in this model the N atom is held in its position on the principle symmetry axis. In this model the bond lengths and angles vary contiunously throughout the motion from the C_3v ammonia to the D_3h transition state. This implies that the transition state can be reached via the normal vibrations of ammonia. This mechanism can be rationalised in terms of hydridisation of orbitals, this is best explained by a diagram and this can be seen below.

Ammonia Inversion Mechanism 2 Orbital Diagram

Inversion Mechanism 2

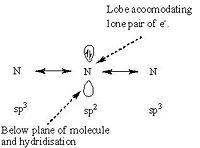
In this case the 3 H atoms are all attracted to and competing for, the lobes this causes the H atoms to collapse into the orbitals and hence either maintain the molecules previous conformation or invert to an alternative conformation. There is a equal probability of inversion or maintenance; of conformation. During this mechanism the bond angles are changing continuously until eventually the transition state angle of 120^o is reached. Since there is an energy difference between the D_3h symmetry and the C_3v symmetry there is a barrier to the inversion and by overcoming this barrier the H atoms move from one conformation to the another. One suggested way that the this energy barrier is penetrated is via quantum tunelling effects. During the molecular reorganisation the physical properties of the molecule will be continually changing since the charge distribution will be changing. One such property is dipole moment as the symmetry increases from C_3v to D_3h the dipole moment should reduce, this is observed by the calculations conducted. Mechanism 2 can be summarised by the diagram below.

Ammonia Inversion Mechanism 2

Inversion Mechanism 2 Summary

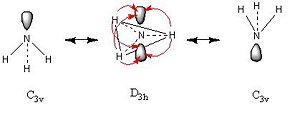
The discussion of the inversion mechanism eluded to quantum tunnelling, this is a highly interesting phenomena in which a particle moves through an energy barrier that is higher than the energy of the particle. A particle achieves tunneling when its wave function predicts its position to be on the higher energy side of an energy barrier then there is a chance that the particle has penetrated the energy barrier rather than moved over it. Quantum tunelling is usually demonstrated (in text books) with electrons in this case however the protons are tunnelling through the energy barrier! This means that calculations concerning quantum tunnelling must take into account a wave function for the nucleus rather than modelling it as an oscillator. This alters the Scödinger equation to give the following:

Where X_N represents the nucleus' wave function and ψ_e represents the electrons wave function. This adds complexity to the quantum tunelling phenomena and takes it outside of the scope of this wiki project.

Inversion mechanism 2 was then modelled using a "scan" calculation this allows investigations to be made into the potential enrgy surface of a transformation. The scan calculation calculates a series of single point energies along the potential energy surface. To follow the inversion the H atoms were allowed to move and whilst the position of the N atom remained constant. The H atoms were defined to move in such a way as to model the 'umbrella' inversion of ammonia, thus following mechanism 2. A pre-calculated scan computation was downloaded from http://www.ch.ic.ac.uk/hunt/teaching/teaching_comp_lab_year3/9d_nh3_inversion.html saved as a .log file and opened using GaussView. The results tab was then selected and the potential energy surface viewed. The potential energy surface can be seen below.