Rep:Mod:jp1612

EX₃ Section

Geometry Information

geometry data

	BH3	BBr3	GaBr3
r(E-X)	1.193	1.956	2.39
θ(X-E-X)	120	120	120

Borane

B3LYP/3-21G level

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000692 0.001800 YES RMS Displacement 0.000441 0.001200 YES Predicted change in Energy=-1.635268D-07 Optimization completed. -- Stationary point found.	optimised Borane molecule

BH₃:B3LYP/6-31G(d,p)

Optimisation file: here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000849 0.001800 YES RMS Displacement 0.000415 0.001200 YES Predicted change in Energy=-1.436188D-07 Optimization completed. -- Stationary point found.	optimised Borane molecule

Gallium (III) Bromide

GaBr₃:B3LYP/LANL2DZ

optimisation file: DOI:10042/91253

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.307730D-12 Optimization completed. -- Stationary point found.	optimised GaBr3 molecule

Boron Tribromide

BBr₃:B3LYP/LANL2DZ

Optimisation file: here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000027 0.001800 YES RMS Displacement 0.000018 0.001200 YES Predicted change in Energy=-2.208681D-10 Optimization completed. -- Stationary point found.	optimised BBr3 molecule

Discussion

Structure Comparison

All three molecules above are trigonal planar molecules and are all electron deficient. We expect GaBr₃>BBr₃>BH₃ for X-Y (X=H,Br; Y=Ga,) bond lengths. This is due to increasing size of atoms from B to Ga and H to Br. All molecules display a X-E-X bond angle of 120° after calculation, this is expected for a trigonal planar molecule

The estimated B-H bond length is 1.15Å, the calculated length is 1.193Å. After considering the error in the calculation and estimated deviations we can say that the calculated bond is very close to a pure covalent bond. The estimated B-Br bond length is 2.04Å and the calculated length is 1.93Å. This is a larger deviation than for the B-H and may be caused by pi conjugation of Bromine and Boron atoms. Gallium is in the same group as Boron but 2 rows down. As we go down group 5 the atoms get larger and the lewis acidity decreases therefore, there will be weaker effects of pi conjugation and a longer B-Br bond. The estimated Ga-Br bond length is 2.42Å and the calculated length is 2.39Å, this shows very strong agreement to the real bond length.

Bonds

A bond is an attraction between atoms. This can be due to electrostatic attraction or dipole interactions. Electron density is shared between the two atoms. The Born-Oppenheimer approximation states that the kinetic energy is neglected, and the nuclei positions are located at the ends of a bond. Atoms have orbitals which are occupied by electrons, it is this orbital overlap that determines the strength of the bond. In reality there will always be energy in the system, vibrations will cause bonds to oscillate causing deviations in bond length. The electrons in the system adapt to changes in the atoms orientations and movements in order to maintain the lowest energy possible.

The type of bonding discussed relates to covalent bonding. There are other types of bonding such as ionic and metallic bonding. The mechanism for the attraction between atoms is different to that of covalent bonding. Ionic bonding is the strong electrostatic attraction between two oppositely charged ions, ionic bonds tend to be stronger than covalent bonds. However, there is no such thing as a pure ionic bond and therefore we describe bonds as having ionic character of which the magnitude is the difference of electronegativities of the two atoms.

An example of a strong covalent bond is a Nitrogen molecule which has a length of only 110pm and bond strength of 945 kJ/mol. It is a diatomic molecule where the two Nitrogen atoms are strongly bound by a triple bond. There is a σ bond and 2 π bonds leading to a triple bond. Halogen molecules are also diatomic but are bound by a single bond. Lone pairs on the atoms repel each other causing elongation and weakening of the bond. However, there are weaker bonds than single bonds. If we take Cl₂ as an example we have a longer bond length of 199pm and a bond strength of 243 kJ/mol. As we go down the Halogen group these bond lengths become longer as bond strength decreases. BH₃ (Borane) readily dimerises to B₂H₆ forming 3c-2e bridging bonds. Borane is electron deficient and this is overcome by formign a dimer. The η-B-H bonds are longer than the terminal B-H bonds suggesting that they are weaker.

GaussView can judge the strength of the interaction between atoms. If the basis set used in calculations is too simple it will recognise there is no bonding interaction and not display a bond. A 3c-2e bond is weaker and longer than a normal B-H bond, Gaussian will deduce that the bond is too long compared to the normal B-H bond and not show a bond,

Frequency Analysis

BH₃:B3LYP/6-31G(d,p)

Frequency file: here

summary data	low modes
	Low frequencies --- -9.6311 -9.6170 -0.1740 0.0005 0.5207 1.0594 Low frequencies --- 1162.9886 1213.1485 1213.1487

wavenumber	Intensity	IR active?	type
1163	93	Yes	Bend (wag)
1213	14	Yes (slight)	Bend (scissoring & rocking)
1213	14	Yes (slight)	Bend (scissoring)
2583	0	No	Stretch (symmetrical)
2716	126	Yes	Stretch (anti-symmetrical)
2716	126	Yes	Stretch (anti-symmetrical)

|

There are 3N-6 vibrational modes for BH₃, this means we can have six IR active modes. A stretch will only appear on the spectrum if there is a change in the dipole moment. This is why we don't see the stretch at 2583cm^-1 because there is no change in dipole moment for a symmetrical stretch. There are only 5 modes which will produce a change in dipole moment and these are IR active.

GaBr₃:B3LYP/6-31G(d,p)

Frequency file: DOI:10042/85100

summary data	low modes
	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

wavenumber	Intensity	IR active?	type
76	3	Yes	Bend
76	3	Yes (slight)	Bend
100	9	Yes (slight)	Bend
197	0	No	Stretch (symmetrical)
316	57	Yes	Stretch
316	57	Yes	Stretch

|

---

It is important to use the same method and basis set for both optimisation and frequency analysis calculations. When the basis set is changed the accuracy of the calculation will also change. When a molecule is optimised we are finding the lowest energy geometry. If we use different basis sets there will be large differences in the energies calculated. Different basis sets have different potential energy surfaces and so if we use different basis sets our molecules are 'sitting' on different curves.

The frequency analysis confirms whether the optimised structure is a transition state or not. If the frequencies are all positive then it is confirmed the optimised structure. A negative frequency is a transition state.

Low frequencies are corresponding to translations and rotations to the optimised structure, and they should be ideally equal to zero.

Molecular Orbitals of BH3

DOI:10042/91248

Linear combination of atomic orbitals (LCAO) is most effective for the core orbitals where the real MOs and calculated MOs are similar. When comparing real and calculated MOs it was seen that LCAO methods were good at predicting the phases of MOs.

For borane, qualitative MO theory is useful and accurate because there is no great difference in the electronegativity and size of hydrogen and boron. There is no significant difference between real and LCAO MOs If we were to examine high energy orbitals which are unoccupied we would see a decrease in accuracy because oribtals start to distort in order to reduce repulsive interactions.

Ammonia

NH₃:B3LYP/6-31G(d,p)

Optimisation

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000012 0.000060 YES RMS Displacement 0.000008 0.000040 YES Predicted change in Energy=-9.844385D-11 Optimization completed. -- Stationary point found.	optimised NH3 molecule

Frequency Analysis

Frequency file: here

summary data	low modes
	Low frequencies --- -0.0130 -0.0021 -0.0016 7.0724 8.1020 8.1023 Low frequencies --- 1089.3849 1693.9369 1693.9369

wavenumber	Intensity	IR active?	type
1089	145	Yes	Bend
1694	14	Yes (slight)	Bend
1694	14	Yes (slight)	Bend
3461	1	No	Stretch
3590	0	No	Stretch
3590	0	Yes	Stretch

|

NBO analysis

DOI:10042/91286

Atom	Charge
H	0.375
N	-1.125

Ammonia Borane

NH₃BH₃:B3LYP/6-31G(d,p)

Optimisation

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000023 0.000060 YES RMS Displacement 0.000010 0.000040 YES Predicted change in Energy=-8.841259D-11 Optimization completed. -- Stationary point found.	optimised NH3BH3

Frequency Analysis

Frequency file: here

summary data	low modes
	Low frequencies --- -5.6933 -0.3189 -0.0466 0.0009 1.1642 1.2396 Low frequencies --- 263.2815 632.9623 638.4593

Wavenumber	Intensity	IR active?	Type
263	0	No	Bend
633	14	Yes (Slightly)	Stretch
638	4	No	Bend
638	4	No	Bend
1069	41	Yes	Bend
1069	41	Yes	Bend
1196	109	Yes	Bend
1204	3	No	Bend
1204	3	No	Bend
1329	114	Yes	Bend
1676	27	Yes	Bend
1676	28	Yes	Bend
2472	67	Yes	Stretch
2532	231	Yes	Stretch
2532	231	Yes	Stretch
3464	3	No	Stretch
3581	28	Yes	Stretch
3581	28	Yes	Stretch

|

Bond Energy

E(NH₃)= -56.5566412367 E(BH₃)= -26.5169826548 E(NH₃BH₃)= -83.2156564967

ΔE= E(NH₃BH₃) - [E(NH₃) + E(BH₃)] ΔE = -0.1420326052 au ΔE = 372.9 kJmol^-1

The strength of the B-N bond can be regarded as a 'medium strength bond'. It is much weaker than a Nitrogen triple bond but stronger than a dihalide X-X bond.

Project Section: Lewis Acids and Bases

Introduction

As touched on previously, there are bonding interactions other than the simple single, double or triple bond. Multi-centre (bridged) bonds exist although they are relatively weak. Diborane, B₂H₆ is an example of a molecule which exhibits 3c-2e bonding. It took chemists several decades to confirm the structure of diborane. Alfred Stock proposed an ethane-like structure however the Boron is electron deficient. L. Pauling and H. Schlessinger proposed the current structure however did not discuss the 3c-2e bonding. Longuet-Higgins, Hedberg and Shomaker, and especially Lipscomb confirmed the 3c-2e bonding. Lipscomb won the Nobel Prize in Chemistry for his work using X-Ray Crystallography and MO theory to describe the 3c-2e bond.

Al₂Cl₄Br₂ is a compound that has been found to also exhibit 3c-2e bonding. There are 5 isomers of this compound which will be analysed computationally.

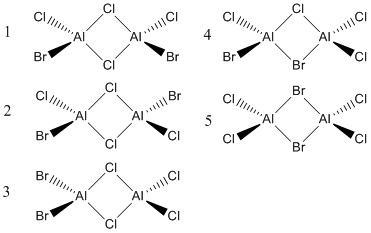
Optimisation

Isomer 1 DOI:10042/102329

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000003 0.000060 YES RMS Displacement 0.000001 0.000040 YES Predicted change in Energy=-1.133901D-12 Optimization completed. -- Stationary point found.	optimised Al2Cl4Br2 molecule

Isomer 2 DOI:10042/102350

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000046 0.000060 YES RMS Displacement 0.000011 0.000040 YES Predicted change in Energy=-4.914331D-11 Optimization completed. -- Stationary point found.	optimised Al2Cl4Br2

Isomer 3 DOI:10042/102380

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000010 0.000060 YES RMS Displacement 0.000003 0.000040 YES Predicted change in Energy=-5.597483D-12 Optimization completed. -- Stationary point found.	optimised Al2Cl4Br2 molecule

Isomer 4 DOI:10042/102387

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000014 0.000060 YES RMS Displacement 0.000005 0.000040 YES Predicted change in Energy=-3.625291D-11 Optimization completed. -- Stationary point found.	optimised Al2Cl4Br2 molecule

Isomer 5 DOI:10042/102434

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000008 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-1.396927D-13 Optimization completed. -- Stationary point found.	optimised Al2Cl4Br2 molecule

The energies from the optimisation calculation can show us the lowest energy conformer and the relative energies of the other conformers. (frequency analysis of the isomers was performed to ensure that no structures were transition states)

Isomer	Relative Energy (kJ/mol)
1	0.1714
2	0.1156
3	-
4	13.75
5	26.30

We can see that the order of energies is as follows:

Isomer 3<Isomer 2<Isomer 1<Isomer 4<Isomer 5

The calculation is not accurate and error must be taken into consideration. There is a ±10kJ error margin in the calculation and so the actual order is:

Isomer 3=Isomer 2= Isomer 1< Isomer 4< Isomer 5

We can see that Isomers 1-3 are very close in energy and can assume degeneracy.

Stability of Conformers

It is important to understand why the molecule is a dimer. Aluminium compounds form dimers readily compared to Boron. Boron being in group 3, it expected that we would see similar bonding. We do see dimerisation in borane to diborane but boron tribromide remains a monomer. Boron tribromide is an electron deficient structure however, the trigonal planar structure allows for sufficient overlap between the filled p orbitals on bromine and the empty p orbitals on boron. We have discussed the strong pi conjugation for boron molecules. As we go down the group to Aluminium we see a weaker effect of pi conjugation as aluminium is larger and there is less overlap between orbitals and so dimerisation is favoured.

The position of the bromine atom is fundamental to the energy of the molecule. Dimerisation is favoured in our molecule to alleviate electron deficiency by increasing electron density around the aluminium atom. This is done by 3c-2e bonding where a sigma lone pair is donated from bromine to aluminium.

Dative bonding model

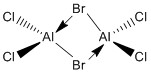
If the only factor determining the energies was the ability to donate a lone pair to the aluminium atom then we can say that Isomer 5 would have the lowest energy. Bromine is less electronegative than chlorine and so would be more likely to donate a lone pair of electrons. However, the calculations show that it has the highest energy of all conformers.

The donating ability is not soley governed by electronegativity. Orbital overlap is another factor that must be considered. The ability of the aluminum orbitals to overlap with the lone pair is key. Chlorine and aluminium will have a relatively better overlap. Chlorine and aluminium can be assumed to have better overlap because they are in the same period. This means that the isomer with the lowest energy must contain two bridging chlorine atoms. This is confirmed by our calculations which show isomers 1-3 having the lowest energies.

We may also consider the possibility of Al-Al interactions. The length of the 3c-2e bridging bonds is an important factor when determining the overlap between Al-Al. The bond angles in the dimer suggest sp³ hybridisation however infra-red spectroscopy display sp² hybridisation.

Each bridging bromine atom increases the energy of the molecule by approximately 13kJ. We can conclude that for Al₂Cl₄Br₂ bridging Br is 13kJ less stable than the bridging Cl. Isomers 1-3 are found to be of lowest energy so we can conclude that orbital overlap is the most influential factor over electronegativity.

NBO analysis may be used to display orbital overlaps of the 3c-2e bonds, this will help us understand the extent of orbital overlap.

Stability of Dimer vs Monomer

We will now compare energies of the lowest energy dimer and its monomers in order to to determine the stability. The fact that the dimer forms would suggest that the dimer is of lower energy.

We will be analysing the AlCl₂Br monomer. It can be seen easily in all isomers except Isomer 3.

Isomer 3 is formed via dynamic exchange from another Isomer. We see the Al-Br bridging bond breaking and then a rotation about the Al-Cl bridging bond.

AlCl2Br can be concluded to be the monomer unit which can form all conformers of the dimer.

DOI:10042/106935

Summary Data	Convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000000 0.000060 YES RMS Displacement 0.000000 0.000040 YES Predicted change in Energy=-5.556512D-16 Optimization completed. -- Stationary point found.

We can now calculate the dissociation energy from the lowest energy conformer. ΔE=E(Al2Cl4Br2)-[2E(AlCl2Br)] ΔE=94.57 kJ/mol

This means that the dimer is 94.57kJ/mol more stable than the monomers. Therefore, we are correct in our theory that the molecule would prefer to dimerise.

Frequency Analysis

Isomer 1 DOI:10042/104680

summary data	low modes
	Low frequencies --- -1.3345 -0.7628 -0.0038 -0.0024 -0.0008 2.2141 Low frequencies --- 17.4965 51.1454 78.5264

|

Isomer 2 DOI:0042/104683

summary data	low modes
	Low frequencies --- -1.8527 -1.5565 -1.1640 0.0014 0.0026 0.0032 Low frequencies --- 18.1841 49.1557 72.8915

|

Isomer 3 DOI:10042/104689

| |

 Low frequencies ---   -0.7884   -0.6014   -0.0022    0.0005    0.0016    2.0598
 Low frequencies ---   18.6308   51.2108   72.2013

|}

|

Isomer 4 DOI:10042/104692

| |

Low frequencies ---   -0.1508   -0.0011    0.0014    0.0015    1.1198    1.8000
 Low frequencies ---   16.9402   55.9182   80.0642

|}

|

Isomer 5 DOI:10042/104698

| |

Low frequencies ---   -0.8418   -0.0025    0.0016    0.0027    1.3042    1.3825
 Low frequencies ---   16.0719   63.6248   86.1129

|}

|

A vibrational mode is only IR active if there is a change in dipole moment.

The main reason we may see different number of peaks in each spectra is due to symmetry of molecules. Isomer 4 which displays C1 Symmetry gives the highest number of peaks. This is probably because both symmetrical and asymmetrical stretches will be IR active because of the lack of symmetry in the molecule.

Isomer 2 shows the least number of peaks. It displays CS symmetry and so is more symmetrical and so any vibration can be displaced by equal motion somewhere else in the molecule. Isomers 1 and 5 both are of C2V symmetry and show the same number of bands however, at different frequencies and intensities.

The terminal or bridging position of the Br atom will effect the position and nature of Al-Br stretching vibrations.

Bridging Stretches:

Isomer'	Mode	Wavenumber	Intensity
Isomer 1	12	279	26
Isomer 2	12	280	29
Isomer 3	13	323	41
Isomer 4	13	289	48
Isomer 5	12	241	100

The stretch being examined is where the bridging atoms move towards each other and away from an aluminium atom. It is seen that Isomer 3 has a considerably larger IR stretch than the others. A higher frequency relates to stronger bonding, the higher frequency in the isomer may be due to the stability of this conformer. From our calculations it was seen that Isomer 3 in fact was the lowest energy isomer so it makes sense that we see stronger bonding. Isomer 5 has the lowest frequency which would indicate weaker relative bonding. Isomer 5 is the highest energy conformer and so it makes sense that it has weaker relative bonding. As we substitute chlorine bridging atoms with bromine atoms we see a noticeable decrease in the IR frequencies. Isomer 4 displays an anomalous result where we see a higher frequency with the subsitution of one bridging chlorine with a bromine. We expect the frequency to be between that of Isomer 5 and Isomers 1-2. What is actually happening is the bromine is behaving like a mainstay on the bond, the chlorine exhibits exaggerated displacement as a result of this.

Terminal Stretches:

Isomer'	Mode	Wavenumber	Intensity
Isomer 1	18	583	277
Isomer 2	18	580	316
Isomer 3	17,18	495,616	105,177
Isomer 4	16,18	493,615	197
Isomer 5	18	618	332

We will be looking at the stretch where the two Al atoms move up/down together which causes elongation/shortening of the Al-X bonds. Comparing the range of frequencies compared to bridging frequencies we see that they are much larger. This is because the terminal bonds are 2c-2e and so are stronger. When we have 2 modes listed, the synchronised movement of Al doesn't occur. One Al atom behaves as an anchor whilst the other moves up/down. We see this behaviour in Isomer 3 and Isomer 4. The lowest mode out of the two will contain the terminal bromine atom. This is due to arguments discussed above that Al-Cl will overlap better causing stronger interactions. We see in Isomer 5 there are no terminal Br atoms and so we see the highest frequency. Isomers 1 and 2 display very similar frequencies because they have one of each terminal bromine and chlorine on a Al atom. The similarities in the frequencies for the terminal Al-Cl bonds and Al-Br bonds across isomers tells us that the positioning of terminal atoms is not as influential compared to the bridging atoms in determining energies of the conformers.

Molecular Orbital Analysis

After energy analysis was performed on the lowest energy conformer we can analyse the Molecular Orbitals. 5 core orbitals are shown ranging from bonding to anti-bonding. By analysing the shapes and characters of these oribtals we seek to rationalise the contributions of the atomic orbitals to the MO.

Energy Calculation file: DOI:10042/107601

MO 37

a: shows a large single phased orbital with no nodal planes. The Al-3s orbital interacts with Cl-3p orbitals strongly to form the shape. Nodal planes between two phases of a p orbital are apparent through the centre of Cl atoms as there is a phase change (red to green) at the centre of the atom.

We see good distribution of electron density around 'a'. This may be because the Al atom is surrounded by only (4) chlorine atoms. This means that there is no inbalance of electronegativty around this area.

b: Shows the nodal plane of the p orbital in the terminal chlorine atom.

c: shows the nodal plane at the centre of the bridging chlorine atom. The electron density is shifted to the terminal chlorine atoms because the p-orbitals are distorted. The Al atom on the right is more electropositive than the left and therefore more electron deficient. This in turn means there is a better overlap between Cl-3p and Al-3s orbitals allowing for the electron deficiency to be better relieved.

What could also occur is that the distortion of the chlorine allows the out of phase mixing between the two (red and green) phases to separate. This will decrease the unfavourable anti-bonding interaction.

d: shows the out of phase mixing at the centre of the molecule. The 'hole' we see displays how the two phases are separated to minimise the interaction between each other.

e: shows the green phase on the left of the molecule. The formation of this phase is similar to that of 'a'. Electrons are attracted to the Aluminium atom, this is because bromine is more polarisable and so electron density can be better polarised to the Al atom.

f: shows the weak in phase mixing between terminal bromine p-orbitals.

Overall we see a strong overlap between Al-3s and Cl-3p orbitals allowing for the greater stability of this conformer. There is an out of phase interaction in the centre of the molecule. There is out of phase mixing between Al-3s orbitals.

MO 39

a: shows the p orbital interaction of the terminal chlorine atom with the large phase formed from the interaction between Al atom and bridging chlorine atom. This is relatively quite a small interaction.

b: shows the nodal plane through the molecule.

c: shows the nodal plane at the centre of both bridging chlorine atoms.

d: shows the bonding interaction between the bridging chlorine atom and the Al atom. The lower electron density around the terminal chlorine atoms may be because this is a pi bonding interaction and so there is naturally a weaker overlap. The interaction between the bridging chlorine atom and Al atom has a dominant sigma characteristic.

e: shows there is no contribution to the system by the terminal bromine atoms.

The MO is overall a weakly bonding orbital.

MO 43

a: shows the electron density (green phase) between the two terminal chlorine atoms. The interaction has sigma characteristics and is therefore a stronger overlap.

b: shows a nodal plane at the centre of the p orbital on the bridging chlorine atoms

c. shows the non-symmetrical formation of the electron cloud in the bonding region across the centre of the molecule.

d: shows the difference in electron densities surrounding the terminal halogens. Bromine has much more diffuse orbitals.

e: There is no orbital contribution from Al atoms. The polarisability of the Al atom contributes to forming diffuse orbitals towards the left of the diagram around the Al and Br atoms.

There is some bonding interactions between the bridging chlorine atoms. We can see weak through space bonding interactions between the terminal chlorine atoms and the bridging chlorine atoms. There are relatively stronger yet weak antibonding interactions between the bridging chlorine atom orbitals and the opposite phase orbital found in between the terminal chlorine atoms because it is closer.

There is weak pi bonding interaction between bridging chlorine atoms because there is not much overlap.

MO 46

a: shows an out of phase interaction between terminal bromine atoms. The orbitals are very diffuse which may be because of the relatively lower electronegativity of bromine and the highly polarisable Al atom. There is weak through space interacions between bridging chlorine atoms and terminal bromine atoms. There is a nodal plane through the centre of the bromine atom.

b: shows weak through space bondingg between terminal and bridging chlorine atoms.

c: shows a weak but relatively stronger pi bonding interaction between bridging bromine atoms.

d: shows an out of phase interaction between the terminal chlorine atoms. There is a nodal plane through the centre of the Chlorine atom. We can see skewing of the orbital towards the polarisable Al atom.

This is an antibonding MO because the main interactions are out of phase ones. The in phase interactions are weaker as they are through space and are not well aligned.

MO 49

a: shows the out of phase mixing between p orbitals of the bridging chlorine atoms. The interaction is purely antibonding as there is no contribution from Al.

b: shows the out of phase interaction between the p orbitals of the terminal chlorine atoms. These are also antibonding and are very localised on the chlorine atoms in order to provide a maximum distance between energetically unfavourable interactions

This MO is overall strongly antibonding as there is no bonding interactions.

Conclusion

We have studied the implications of the positioning of the bromine atom, whether it is in the bridging or terminal position in a dimer, Al₂Cl₄Br₂. Bromine in a bridging position can lead to relative destabilisation of the dimer. We look at predicted IR data and also MO analysis to demonstrate the effects of the positioning on the energy of the molecule.

We could extend this experiment by choosing different group 3 and 7 elements and performing calculations to analyse the energies in these molecules. Compounds such as [R₂GaX]₂ [R₂InCl]_n can be analysed. We know the indium complex adopts larger coordination numbers and this can be a further explored by examining the energies in the molecule.