Introduction
Using Gaussian 5.0, the molecules NH3, N2, H2 and S2 were optimised using RB3LYP as the calculation method and 6-31G(d,p) as the basis set. To ensure that optimisation was carried out successfully, the item table was included so that the values of the force could be reported. All the molecules calculated showed convergence in the item table, showing that the energy reached a stationary point since Force is the first differential of energy. To ascertain that the stationary point is a minimum, rather than a maximum which could correspond to a transition state, the frequency of vibration (which corresponds to the second derivative of energy) was calculated. All the values of frequency were positive, showing that the stationary point of energy is a minima.
The reaction energy of the Haber Bosch reaction N2 + H2 → NH3 was calculated as well and found to be -146.47849401 kJ/mol. Using Gaussian, the molecular orbitals of H2CO and S2 were also visualised to predict their reactivity and bonding properties.
Part 1: NH3
Molecular Information
| NH3 molecule
|
|
|
| Molecule information
|
| Name
|
Ammonia
|
| Calculation Type
|
OPT, FREQ
|
| Calculation Method
|
RB3LYP
|
| Basis Set
|
6-31G(d,p)
|
| Final Energy E(RB3LYP) in
atomic units (au)
|
-56.55776873
|
| RMS gradient (au)
|
0.00000485
|
| Point Group
|
C3v
|
| Link to complete NH3
optimization .log file
|
The optimisation file is linked to here
|
| Optimised N-H bond distance (angstroms)
|
1.01798
|
| Optimised H-N-H bond angle (o)
|
105.471
|
Item Table:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
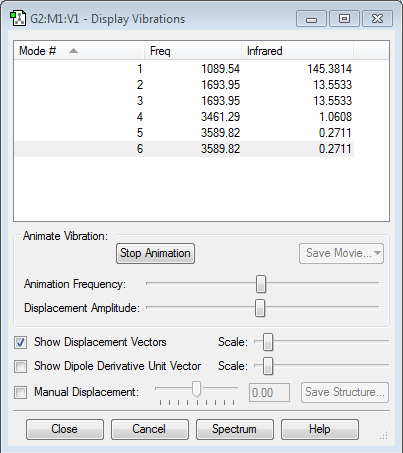
Vibrational Analysis
 |
Using the 3N-6 rule, 6 modes of vibrations are expected. Modes 2 and 3, as well as 5 and 6 are degenerate. Modes 1, 2 and 3 are bending vibrations while modes 4, 5 and 6 are bond stretching vibrations. Mode 4 is highly symmetric. The umbrella mode is vibrational mode 1. Since the intensity of vibrational modes 4,5 and 6 are very low, they will be lost due to background signals. Since modes 2 and 3 are degenerate, 2 bands are expected to be seen in an experimental spectrum of gaseous ammonia.
|
Charge Analysis
 |
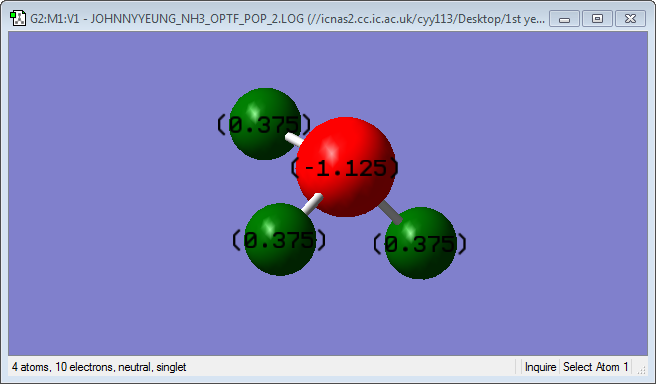Nitrogen has a charge of -1.125, while hydrogen has a charge of 0.375. Nitrogen bears the partially negative charge as it has a much high electronegativity than hydrogen and pulls electron density towards itself. The Pauling electronegativity values of nitrogen and hydrogen are 3.04 and 2.20 respectively. {1}
|
Part 2: N2
Molecular Information
| N2 molecule
|
|
|
| Molecule information
|
| Name
|
Nitrogen
|
| Calculation Type
|
OPT, FREQ
|
| Calculation Method
|
RB3LYP
|
| Basis Set
|
6-31G(d,p)
|
| Final Energy E(RB3LYP) in
atomic units (au)
|
-109.52412868
|
| RMS gradient (au)
|
0.00000060
|
| Point Group
|
D∞h
|
| Link to complete N2
optimization .log file
|
The optimisation file is linked to here
|
| Optimised N-N bond distance (angstroms)
|
1.10550
|
| Optimised bond angle in N2 (o)
|
N/A as 3 atoms are required to calculate a bond angle.
|
Item Table:
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
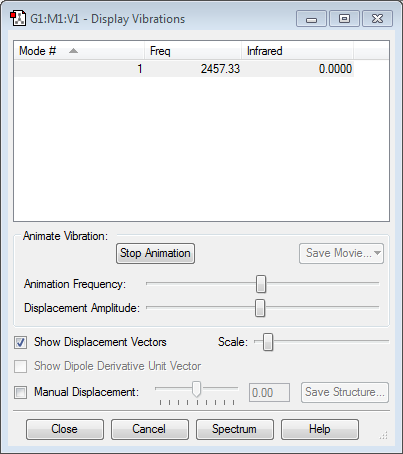
Vibrational Analysis
 |
Using the 3N-5 rule, 1 mode of vibration is expected. The mode of vibration is a symmetric stretch. However, this vibration does not cause a change in dipole moment and thus not IR active. Hence, no band will be observed in an IR spectrum.
|
Charge Analysis
 |
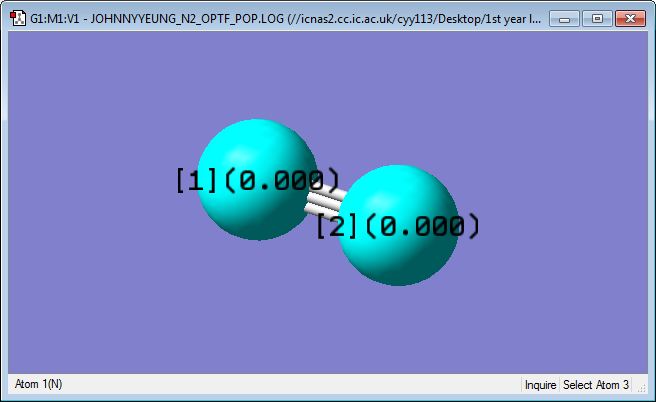Both nitrogen atoms have a charge of 0. This is expected, as both nitrogen atoms have the same electronegativity and the difference in electronegativity is 0.
|
Part 3: H2
Molecular Information
| H2 molecule
|
|
|
| Molecule information
|
| Name
|
Hydrogen
|
| Calculation Type
|
OPT, FREQ
|
| Calculation Method
|
RB3LYP
|
| Basis Set
|
6-31G(d,p)
|
| Final Energy E(RB3LYP) in
atomic units (au)
|
-1.17853936
|
| RMS gradient (au)
|
0.00000017
|
| Point Group
|
D∞h
|
| Link to complete H2
optimization .log file
|
The optimisation file is linked to here
|
| Optimised H-H bond distance (angstroms)
|
0.74279
|
| Optimised bond angle in H2 (o)
|
N/A as 3 atoms are required to calculate a bond angle.
|
Item Table:
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
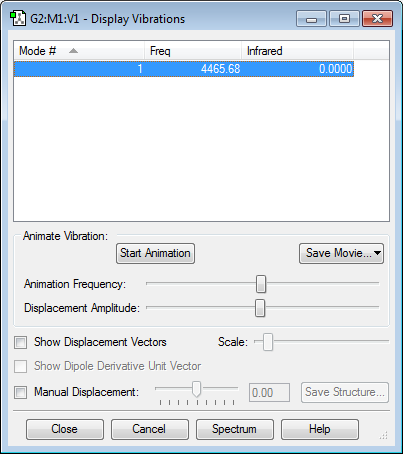
Vibrational Analysis
 |
Using the 3N-5 rule, 1 mode of vibration is expected. The mode of vibration is a symmetric stretch. However, this vibration does not cause a change in dipole moment and thus not IR active. Hence, no band will be observed in an IR spectrum.
|
Charge Analysis
 |
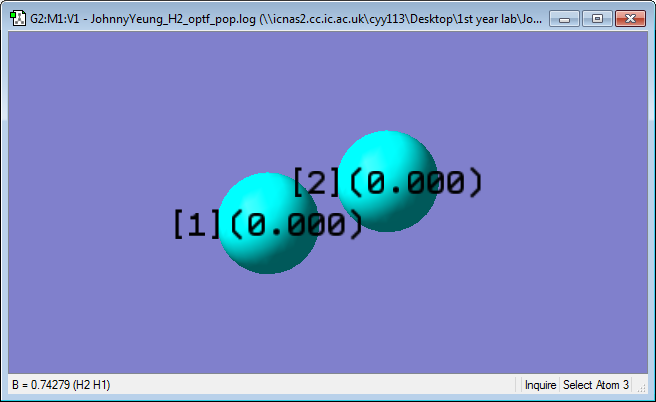Both hydrogen atoms have a charge of 0. This is expected, as both hydrogen atoms have the same electronegativity and the difference in electronegativity is 0.
|
Part 4: Reaction Energy
The following energy values (in au) were obtained in order to calculate the energy of the Haber-Bosch reaction:
| E(NH3) |
-56.55776873
|
| 2*E(NH3) |
-113.11553746
|
| E(N2) |
-109.52412868
|
| E(H2) |
-1.17853936
|
| 3*E(H2) |
-3.53561808
|
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] |
-0.0557907
|
Using a web based converter, the energy of the Haber-Bosch reaction is -146.47849401 kJ/mol. Thus, NH3 is more stable than N2 and H2.
Part 5: A choice of small molecule: H2CO
Molecular Information
| H2CO molecule
|
|
|
| Molecule information
|
| Name
|
Formaldehyde
|
| Calculation Type
|
OPT, FREQ
|
| Calculation Method
|
RB3LYP
|
| Basis Set
|
6-31G(d,p)
|
| Final Energy E(RB3LYP) in
atomic units (au)
|
-114.50319933
|
| RMS gradient (au)
|
0.00007386
|
| Point Group
|
Cs
|
| Link to complete H2CO
optimization .log file
|
The optimisation file is linked to here
|
| Optimised bond distances (angstroms)
|
(C=O)=1.20676; (C-H)=1.11057
|
| Optimised bond angles (o)
|
(H-C=O)=122.395; (H-C-H)=115.219
|
Item Table:
Item Value Threshold Converged?
Maximum Force 0.000197 0.000450 YES
RMS Force 0.000085 0.000300 YES
Maximum Displacement 0.000270 0.001800 YES
RMS Displacement 0.000149 0.001200 YES
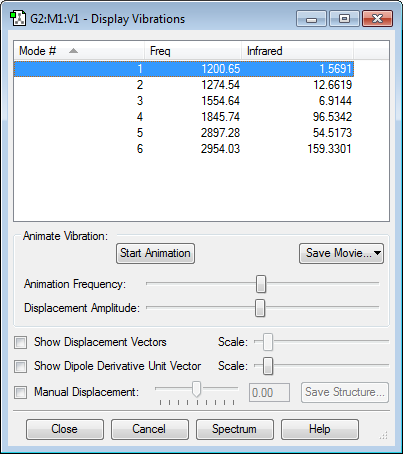
Vibrational Analysis
 |
Using the 3N-6 rule, 6 modes of vibrations are expected. All the vibrational modes cause a change in dipole moment and thus will be IR active. Since the intensity of vibrational modes 1 and 3 are very low, they will be lost due to background signals. Thus, 4 bands are expected to be seen in an experimental spectrum of H2CO.
|
Charge Analysis
 |
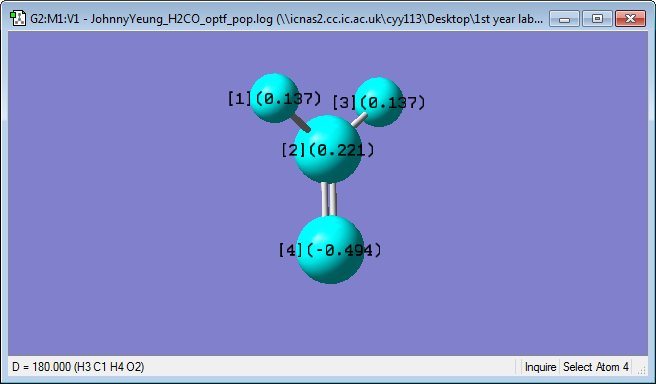Oxygen has a charge of -0.494, Carbon has a charge of 0.221, while Hydrogen has a charge of 0.137. Oxygen bears the partially negative charge as it has a much higher electronegativity (3.44; Pauling scale) than hydrogen (2.20; Pauling scale) and carbon (2.55; Pauling scale) and pulls electron density towards itself.
|
Molecular Orbital (MO) Analysis
 |
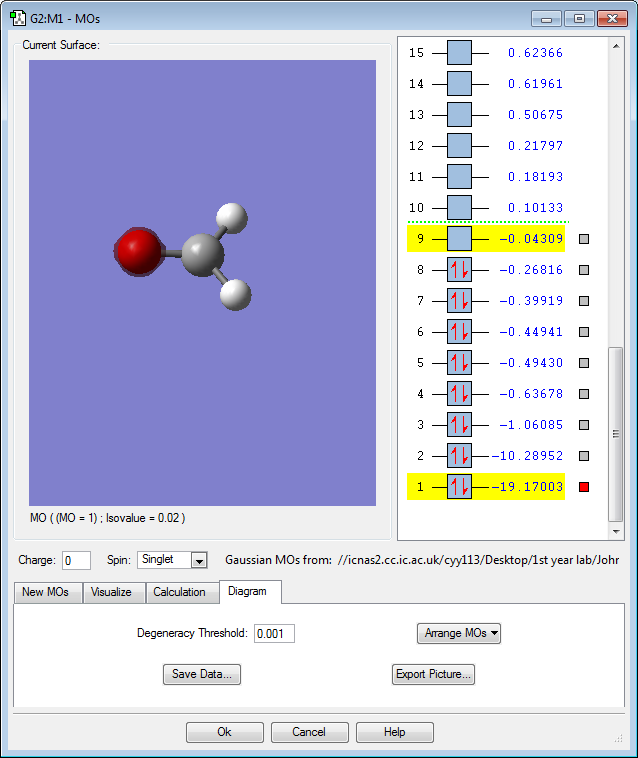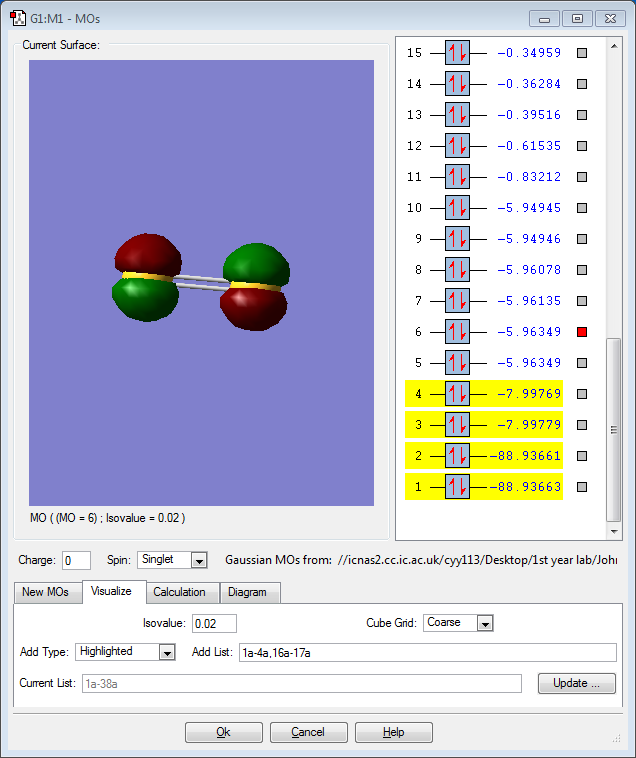
MO 1: The 1s orbital of oxygen contributes to this non-bonding molecular orbital. The MO is very low in energy, with a significantly negative value of -19.2. The 1s orbitals of oxygen and carbon are too small and the electron density is very close to the nucleus, so no overlap is possible. Since the MO is too low in energy, it is usually left out of the MO diagram as it does not contribute significantly to any reactivity of H2CO.
|
 |
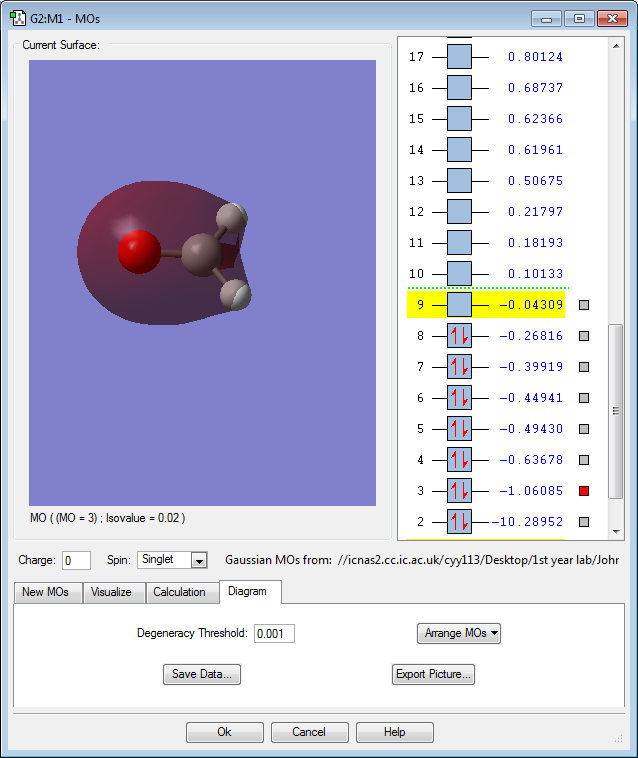MO 3: The 2s orbitals of oxygen, carbon and 1s orbitals of hydrogen contributes to form this bonding molecular orbital. The MO is relatively low in energy, with a negative value of -1.06. It is an occupied orbital. Because it is also a bonding orbital, occupying this will have a stabilizing effect on the molecule.
|
 |
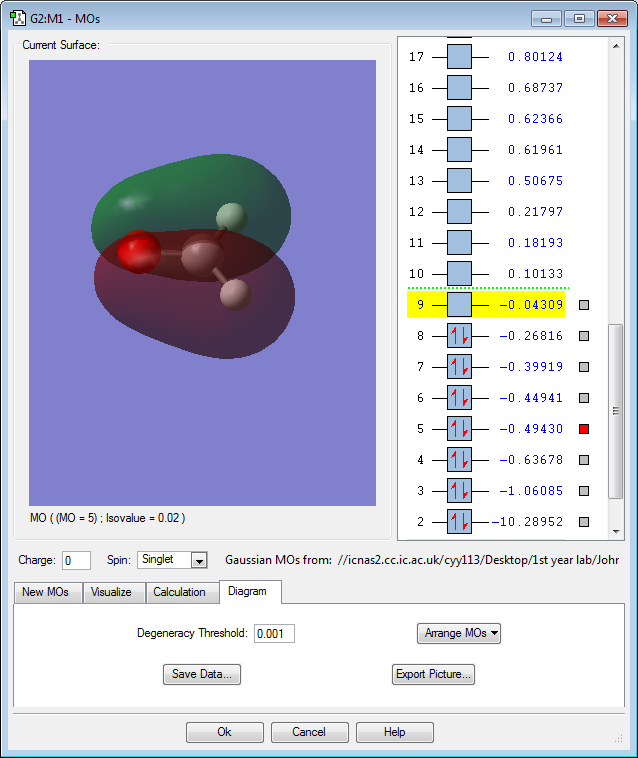MO 5: The 2s orbitals of oxygen, carbon and one hydrogen contribute in an in-phase manner, while the other hydrogen contributes in an out-of-phase manner. There is 1 nodal plane. This MO is rather high in energy with a slightly negative value of -0.49au.
|
 |
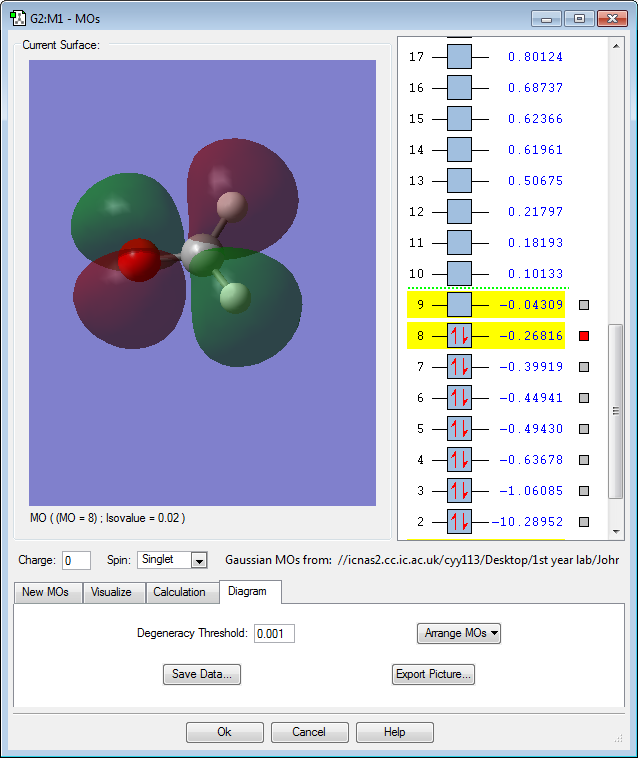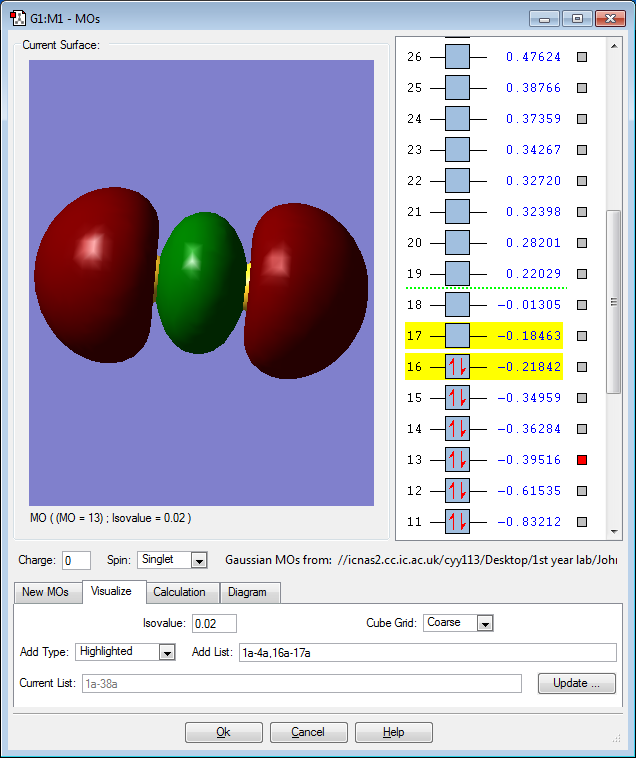
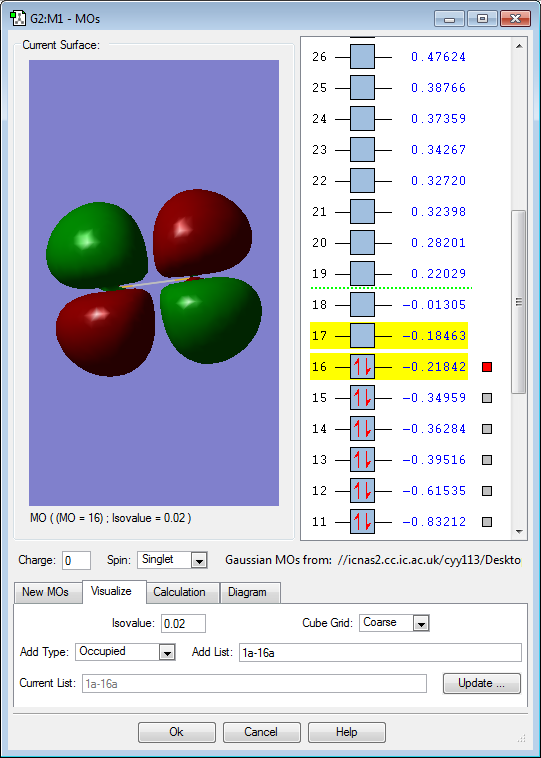
MO 8: The 2p atomic orbitals of carbon and oxygen contribute to form this antibonding molecular orbital. The MO is rather high in energy with only a slightly negative value of -0.29au. This is the highest occupied molecular orbital (HOMO) and it has the highest number of nodes of all the occupied molecular orbitals. Because it is an antibonding orbital and is occupied, this will have a destabilizing effect on the molecule. Protonating this oxygen increases the effective nuclear charge of oxygen and lowers the energy of its atomic orbital. The energy of the resulting molecular orbital is lowered making it more stable. This explains why the carbonyl oxygen is protonated first in an acid-catalysed nucleophile attack reaction.(Keeler and Wothers, 2014)
|
 |
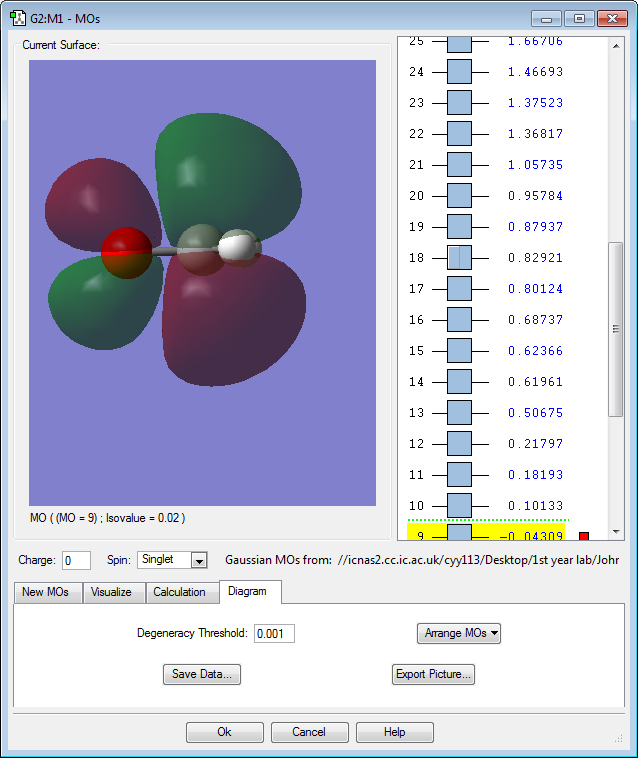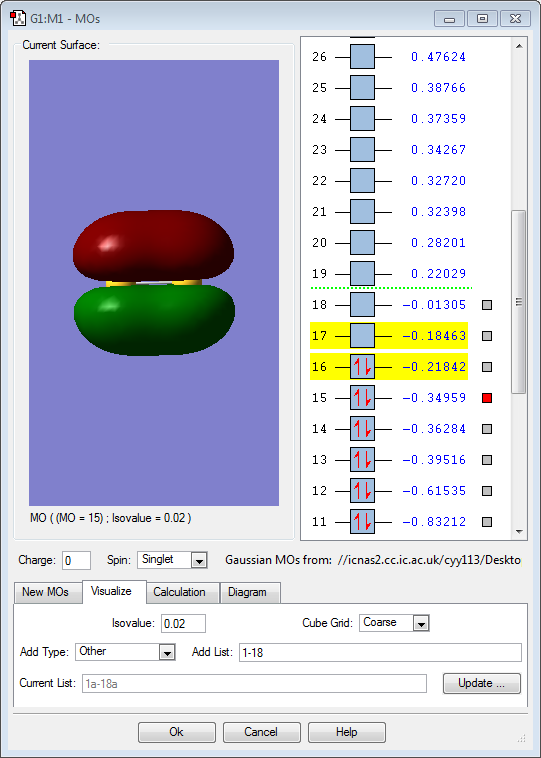
MO 9: The 2p atomic orbitals of carbon and oxygen contribute to form this antibonding molecular orbital. The MO is rather high in energy with only a slightly negative value of -0.04au. This is the lowest occupied molecular orbital (LUMO) and it has the smallest number of nodes of all the unoccupied molecular orbitals. Because it is an antibonding orbital and is unoccupied, this will have a stabilizing effect on the molecule. The largest lobe on the molecule is 107o with respect to the (C=O) bond, thus the nucleophile approaches the carbonyl compound with an angle of 107o, known as the Burgi-Dunitz Angle.(Clayden, 2001)
|
Part 6: Another choice of small molecule: S2
Molecular Information
| S2 molecule
|
|
|
| Molecule information
|
| Name
|
Disulfur
|
| Calculation Type
|
OPT, FREQ
|
| Calculation Method
|
RB3LYP
|
| Basis Set
|
6-31G(d,p)
|
| Final Energy E(RB3LYP) in
atomic units (au)
|
-796.32599779
|
| RMS gradient (au)
|
0.00000372
|
| Point Group
|
D∞h
|
| Link to complete S2
optimization .log file
|
The optimisation file is linked to here
|
| Optimised S=S bond distance (angstroms)
|
1.92943
|
| Optimised S=S bond angle (o)
|
N/A as 3 atoms are required to calculate a bond angle.
|
Item Table:
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000011 0.001800 YES
RMS Displacement 0.000016 0.001200 YES
Vibrational Analysis
 |
Using the 3N-5 rule, 1 mode of vibration is expected. The mode of vibration is a symmetric stretch. However, this vibration does not cause a change in dipole moment and thus not IR active. Hence, no band will be observed in an IR spectrum.
|
Charge Analysis
 |
Both sulfur atoms have a charge of 0. This is expected, as both sulfur atoms have the same electronegativity and the difference in electronegativity is 0.
|
Molecular Orbital (MO) Analysis
 |
MO 1: The 1s orbital of one sulfur atom contributes to this non-bonding molecular orbital. The MO is very low in energy, with a significant negative value of -88.9. This MO and MO 2 are degenerate orbitals having the same energy as the other 1s orbital of the other sulfur atom contributes to MO 2. The 1s orbitals are too small and the electron density is very close to the nucleus, so no overlap is possible. Degenerate orbitals are formed because both 1s orbitals of sulfur are of the same energy. Since the MO is too low in energy, it is usually left out of the MO diagram as it does not contribute significantly to any reactivity of S2.
|
 |
MO 6: The 2p orbital of one sulfur atom contributes to form this non-bonding molecular orbital. The MO is low in energy, with a negative value of -5.96. MO 5, 6, 7, 8, 9 and 10 are degenerate orbitals having the same energy. There are 3 degenerate 2p orbitals per sulfur atom that are orthogonal to each other and they are too small to overlap. 2 sulfur atoms contribute a total of 6 2p orbitals to generate a total of 6 non-bonding MOs.
|
 |
MO 13: Two 3p orbitals contribute to form this σ bonding molecular orbital in a head-on overlap. This MO is rather high in energy with a slightly negative value of -0.40au. It is an occupied orbital. Because it is a bonding orbital, occupying it will stabilize the molecule.
|
 |
MO 15: Two 2p orbitals of sulfur contribute to form this π bonding molecular orbital in a side-on overlap. There is electron density above and below the nodal plane. This MO is also rather high in energy with a slightly negative value of -0.35au. It is an occupied orbital. Because it is also a bonding orbital, occupying this will have a stabilizing effect on the molecule and cancels out the destabilizing effect in MO 15.
|
 |
MO 16: Two 3p atomic orbitals contribute to form this π antibonding molecular orbital. It is gerade. The MO is rather high in energy with only a slightly negative value of -0.22au. This is the highest occupied molecular orbital (HOMO) and it has the greatest number of nodes of all the occupied molecular orbitals. Because it is an antibonding orbital and is occupied, this will have a destabilizing effect on the molecule. Nevertheless, the molecule is still stable due to more extensive bonding contributions from other molecular orbitals.
|
Part 7: References
1. Keeler J, Wothers P. Chemical structure and reactivity. Oxford: Oxford University Press; 2014.
2. Clayden J. Organic chemistry. Oxford: Oxford University Press; 2001.
3. What is Pauling's scale used for and how does it work? | Socratic [Internet]. Socratic.org. 2016 [cited 11 March 2016]. Available from: http://socratic.org/questions/what-is-the-paulings-scale-used-for-and-how-does-it-work
