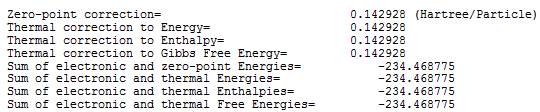Joe McDermott Wiki, Module 3

The Cope Rearrangement

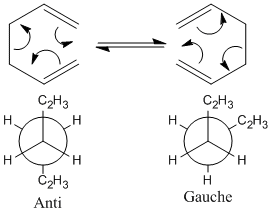
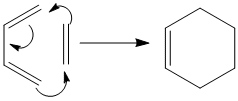
The Cope rearrangement of 1,5-hexadiene is investigated in this project (the mechanism with Newman projections shown in figure 1) using analytical techniques on Gaussview 5.0.9. The mechanism in figure 1 shows the Cope rearrangement to be a [3,3]- sigmatropic shift reaction; an example of a peri-cyclic reaction, which is a reaction that proceeds via a cyclic conjugated transition state. The aim of the project is to determine the concerted nature of the Cope rearrangement.


Figure 1

Optimization of Reactants and Products

Table 1 shows the energy and structure of the ten possible conformers of 1,5-hexadiene; obtained using Gaussview 5.0.9 with the Hartree Fock method and 3-21G basis set.

Energy/ Hartree	Relative energy/ kcalmol^-1	Point Group
-231.6926	0.04	C₂
-231.6925	0.08	C_i
-231.6891	2.25	C_2h
-231.6909	1.06	C₁
-231.6877	3.10	C₂
-231.6917	0.60	C₂
-231.6927	0.00	C₁
-231.6915	0.71	C₂
-231.6896	1.91	C₁
-231.6892	2.20	C₁

Table1

The Hartree Fock optimization method does not take electron correlation into consideration when preforming calculations therefore the calculations are much faster than other optimization methods such as DFT. All the results presented in table 1 are a close match to those provided on the Module 3 wiki page. When thinking about the sterics of the possible conformers it is expected that the anti conformers will have lower steric clashing than the gauche conformers and therefore be lower in energy thus being the most stable; however this expectation is not observed.

The gauche 3 conformer is found to be the most stable, with the anti 1&2 conformers being very close in energy to gauche 3; so a re-optimization is preformed on the three conformers to determine which is truly the most stable using a higher basis set on Gaussview 5.0.9; B3LYP method and 6-31G(d) basis set are used, the results are shown in table 2.

Energy/ Hartree	Relative energy/ kcalmol^-1	Point Group
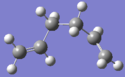
-234.6113	0.28	C₁
-234.6118	0.00	C₂
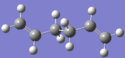
-234.6117	0.04	C_i

Table 2

The re-optimization does not cause any major changes to the structures but does produce the conformers in a more stable orientation. The minor change comes in the form of the dihedral angles of the terminal carbons by plus 4.1^° going from the HF to the DFT method. The order of stability also changes with the gauche conformer now the highest energy conformer and the anti 1 becoming the lowest in energy.

It can be concluded that the DFT method produces a more accurate representation of the conformers than the HF method.

IR spectrum

The IR spectrum shown in figure 2 obtained using Gaussview 5.0.9 B3LYP method and 6-31G(d) basis set.


DOI:10042/to-11122
Figure 2

An IR spectrum is necessary to determine if the conformer is fully optimized as the presences of negative vibrational frequencies is an indication of bond strain and therefore a non-fully optimized molecule. All the frequencies of the anti 2 conformer are positive so the conformer can be said to be fully optimized with 42 different vibrations.

Figures 3 and 4 show the thermochemistry results for the anti 2 conformer at 298.15k and for 0.00k respectively.


Figure 3


Figure 4

Optimizing the Chair and Boat Transition Structures

In this section of the project the transition states of the Cope rearrangement are investigated, analyzing possible transition states to be in the chair or boat orientations.

Chair conformer

A chair conformer optimized using Gaussview 5.0.9 with HF/3-21G method/basis set.

Firstly the optimization is set to TS (berny) optimization, the resultant shows that the conformer is in the transition state of the Cope rearrangement along with a imaginary vibrational frequency at -817.94cm^-1. The bond length of the terminal allyl fragments are 2.0205Å and 2.0204Å.

Secondly the a frozen coordinates approach was taken; the distance between terminal allyl fragments was set to 2.2Å and an optimization carried out, the conformer is then re-optimized without the terminal allyl fragments frozen. This approach obtained bond lengths of the terminal allyl fragments both of 2.0200Å and an optimized .

It can be seen that both methods produce similar results.

An IRC calculation was then preformed on the chair conformer with 50 calculation points and calculated force constants at every point. The graphs obtained are the total energy (top) and the RMS gradient (bottom), figure 5 and the of the conformer is shown in figure 6.


Figure 5


Figure 6

The low RMS gradient shown indicates that the optimization is complete, the structure and energy (-231.6917) of the chair transition state very closely matches that of the gauche 2 conformer.

Boat conformer

The boat conformer is optimized with the QST2 TS method using Gaussview 5.0.9. The optimization failed as the produced resembles a chair conformer.

The optimization is repeated but with the dihedral angles of the four central atoms changed to 100^° and the angle between all four of these carbons changed to 0^° to produce the and imaginary vibrational frequency of -840.13cm ^-1.

An IRC calculation was then preformed on the boat conformer with 50 calculation points and calculated force constants at every point. The graphs obtained are the total energy (top) and the RMS gradient (bottom), figure 7 and the of the conformer is shown in figure 8.


Figure 7


Figure 8

The low RMS gradient shown indicates that the optimization is complete, the structure and energy (-231.6927) of the boat transition state very closely matches that of the gauche 3 conformer.

Activation Energies

The summary of energies and activation energies are shown in tables 3 and 4 respectively.

	Sum of electronic and thermal energies DFT (B3LYP) 0.00k/Hartree	Sum of electronic and thermal energies DFT (B3LYP) 298.15k/Hartree
Chair TS	-234.4112	-234.4052
Boat TS	-234.3981	-234.3926
Anti 2 conformer	-234.4619	-234.4688

Table 3

	B3LPY/6-31G(d) 0.00k/kcal mol^-1	B3LPY/6-31G(d) 298.15k/kcal mol^-1	Expt. 0.00k/kcal mol^-1
ΔE (Chair)	31.69	39.73	33.5 ± 0.5
ΔE (Boat)	40.30	47.77	44.7 ± 2.0

Table 4

The calculated activation energies at both 0.00k and 298.15k follow the same trend of the chair transition state having a lower activation energy than the boat transition state. The reduced amount of steric clashing between hydrogen atoms in the chair transition state compared to the boat transition causes the chair to have the lower activation energy. The orientation of the chair transition state means its more favorable for secondary orbital overlap interactions which will cause destabilization. The destabilizing overlap is greater in the boat transition state than in the chair transition state as the terminal carbon atoms are closer in the boat transition state than in the chair transition state.

The Diels Alder Cycloaddition

This section of the projected will investigated a cycloaddition Diels Alder reaction. The cyclosaddtion will be between 1,5-butadiene and ethene to produce cyclohexene. The mechanism for the reaction is shown in figure 9.


Figure 9

cis-Butadiene and Ethene

Both cis-butadiene and ethene are optimized using Gaussview 5.0.9 with a semi-empirical method and AM1 level of theory, this also produced molecular orbitals for both, the HOMO and LUMO graphical representations of which are shown in table 5.

Molecule	HOMO	LUMO
cis-Butadiene
Ethene

Table 5

The cis-butadiene HOMO can be seen to be antisymmetrical with respect to the plane between the four central carbons that is perpendicular to the plane of the molecule; the LUMO can be seen to be symmetrical with respect to the same plane.

The ethene HOMO can be seen to be symmetrical with respect to the plane between the carbon carbon double bond that is perpendicular to the plane of the molecule; the LUMO can be seen to be antisymmetrical with respect to the same plane.

Cycloaddition Transition state

The cycloaddition transition state is found by freezing the distance between terminal carbons and optimizing to a minimum using Gaussview 5.0.9 with a semi-empirical method and AM1 level of theory, then the coordinates are unfrozen and optimized to a TS(berny) this also produced molecular orbitals for both, the HOMO and LUMO graphical representations of which along with the structure of the transition state are shown in table 6.

Structure

HOMO

LUMO

Table 6

The reaction can be seen to proceed via a [4π+2π] syn-cycloaddition as from the imaginary vibrational frequency calculated at -956.24cm^-1. The vibration shows bonds to be forming simultaneously so it is in agreement with the theory that says the reaction is concerted. The next lowest vibrational frequency calculated is at 147.26cm^-1 and displays asynchronous bond formation and relates to cyclisation that is higher in energy than the cycloaddition.

It can be seen in the molecular orbitals above for the transition state that the HOMO consists of the combination of the ethene LUMO and the cis-butadiene HOMO; also the LUMO consists of the combination of the ethene HOMO and the cis-butadiene LUMO. This occurs as the orbitals combining are of the same symmetry and produce stabilizing orbital orbital overlap. The molecular orbitals for the transition state also show the HOMO to be donating π electrons from cis-butadiene to the π* orbital on ethene which forms the two σ bonds; the LUMO donates π electrons from ethene to π* orbital of cis-butadiene to form the carbon carbon double bond.

The length of the single bonds is found to be 1.397Å and the length of double bonds is found to be 1.382Å; the single bonds are shorter than expected as started from a double bond and the double bonds are longer than expected^[1] as π electrons leave to produce a new bond. The distance between terminal carbons is found to be 2.119Å, this distance is larger than both the single and double bonds present so the ethene is said not be be fully bonded i.e transition state.

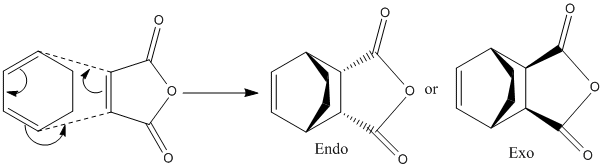
Regioselectivity of the Dield Alder Reaction

Here the transition state is found by freezing the distance between terminal carbons and optimizing to a minimum using Gaussview 5.0.9 with a semi-empirical method and AM1 level of theory, then the coordinates are unfrozen and optimized to a TS(berny) this also produced molecular orbitals for the endo and exo, the HOMO, LUMO and LUMO+1 are graphical representations of which are shown in table 8; the structure of the transition states shown in table 7 and the mechanism for the reaction is shown in figure 10.


Figure 10

Endo

Exo

Table 7

Orbital	Endo	Exo
HOMO
LUMO
LUMO+1

Table 8

Imaginary vibrational frequencies found for both structures; the endo at -806.42cm^-1 and the exo at -812.27cm^-1. The terminal carbon bond lengths for the endo and exo products are found to be 2.162Å and 2.170Å respectively.

All of the molecular orbitals are shown to have no symmetry in the one axis and to be antisymmetric in the other; the oxygen atom regions display large nodes that coordinate electron density towards the carbon carbon double bond which will favor electron donation to produce bonds with the cyclohexdadiene.

The endo transition state is found to have a lower energy than the exo transition state; -0.051504 Hartree compared to -0.50419 Hartree. This proves that the endo structure is the kinetic product; this is due to there being a greater amount of steric clashing in the endo structure compared to the exo structure therefore the endo product is more stable due to secondary orbital effects^[2].

Conclusion

This project deals with optimizing transition states using the HF/3-21G, Semi-Empirical/AM1 and DFT/6-31G; accuracies of which are in increasing order. By obtaining imaginary (negative) vibrational frequencies it is possible to confirm that the structure being investigated are in transition states; the IRC plots produced show how the energy changes when the reaction moves from products to reactants via the transition state therefore providing an explanation for the favored product and transition state.

The cope rearrangement was investigated with two different optimization methods to provide a more complex analysis of the three lowest energy transition states. From analyzing the more complex Diels Alder reaction it can be concluded that the endo product is preferred to the exo product due to secondary orbital overlap.

References

↑ R. Dias, Organic Chemistry, http://www.odu.edu/~rfdias/chem311/02BONDING.pdf
↑ Ian Fleming, Frontier orbitals and organic chemical reactions, John Wiley & Sons, 2006, 106-107