Jump to content

Rep:Mod:joewikiwiki

From ChemWiki

Joe McDermott Wiki, Module 2

BH3

Optimization

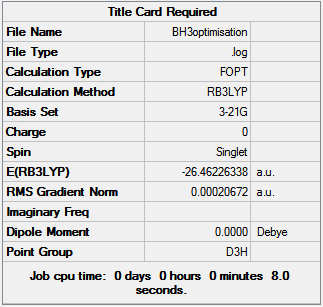
Using Gaussview 5.0.9 a BH3 molecule was created and all three B-H bonds set to 1.50Å. The created molecule is then optimized using the B3LYP method and 3-21G basis set as both recommended to be the most efficient method and basis set to optimize the simple BH3 molecule; the resulting B-H bond length is 1.19Å and the H-B-H bond angle is 120o. Figure 1 shows the results summary from the optimization.

Figure 1

summary of BH3 optimization

The final energy of the molecule is -26.46 Hartree, the RMS gradient is very close to zero (0.00021) indicating the optimization has finished and the total time of the optimization is 8 seconds, a small amount of time was to be expected as the molecule is very simple. BH3 does not poses a dipole due to the D3h point group and means that all hydrogen atoms have the same orientation to the boron.


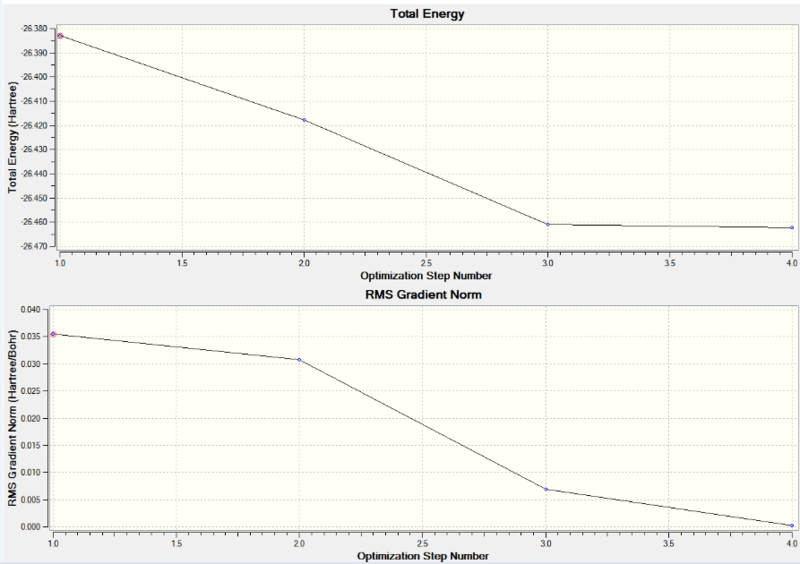
Figure 2 shows two graphs, the top graph is for the total energy through the optimization and the bottom graph is for the RMS gradient through the optimization BH3.

Figure 2

Graphs for BH3 optimization

The graph for the total energy shows a decrease in energy for the first few optimization steps before reaching a minimum value, the same trend is shown for the graph of RMS gradient through the optimization. The two graphs show that the molecule was fully optimized after four steps as there is no longer a change in total energy and the RMS gradient is less than 0.001 therefore the displacement of each hydrogen after four steps is too small to cause any further change geometry.

IR spectrum analysis

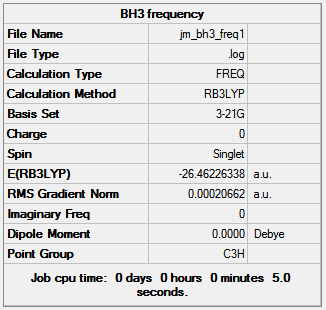
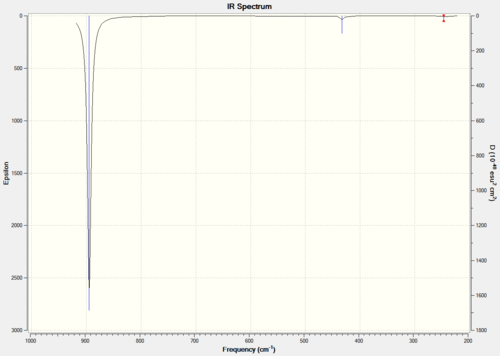
Gaussview 5.0.9 used again to obtain an IR spectrum with the B3LYP method and 3-21G basis set. This is necessary as to determine whether the BH3 molecule is fully optimized, negative stretching frequencies will mean the molecule is still in its transition state, i.e not fully optimized; positive stretching frequencies will mean the molecule is in its ground state and therefore is fully optimized. The summary of the IR spectrum calculation is shown in figure 3.

Figure 3

Summary for BH3 IR frequency

The total energy is the same as the optimized molecule, -26.46 Hartree. There is a change in point group from D3h to C3h which indicates the molecule is no longer planer after the IR frequency calculations but the lack of dipole moment means the molecule is still planer so Gaussview must have made a mistake.

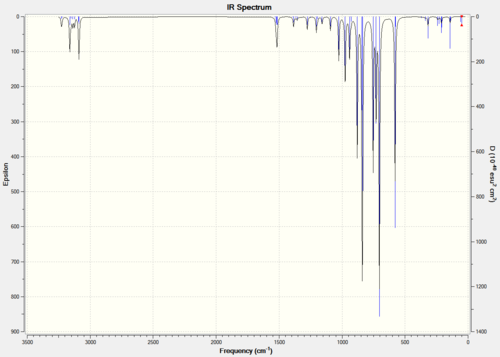
Figure 4 shows the obtained IR spectrum and table 1 shows the calculated IR spectrum data both for BH3.

Figure 4
IR spectrum


No Stretch Wavenumber (cm-1) Intensity Symmetry (D3h)
1 Wagging 1144 92.9 A"
2 Scissoring 1204 12.3 E'
3 Rocking 1204 12.3 E'
4 Symmetrical stretch 2598 0 A'
5 Antisymmetrical stretch 2737 103.7 E'
6 Antisymmetrical stretch 2737 103.7 E'

Table 1

The IR spectrum shows three peaks even though Gaussview calculated six vibrational frequencies for the BH3 molecule. The first reason for this is the degree of degeneracy between vibrations two & three and five & six (shown in table 1), the degeneracy causes the peaks to be superimposed over one and other. The second reason is that vibration four has an intensity of zero due to the vibration not having a change in dipole moment as it is perfectly symmetrical; for a vibration to be shown in an IR spectrum it needs to have a change in dipole moment. Considering these reasons the IR spectrum produced appears to correspond to the calculation results.

Molecular orbital (MO) results for BH3

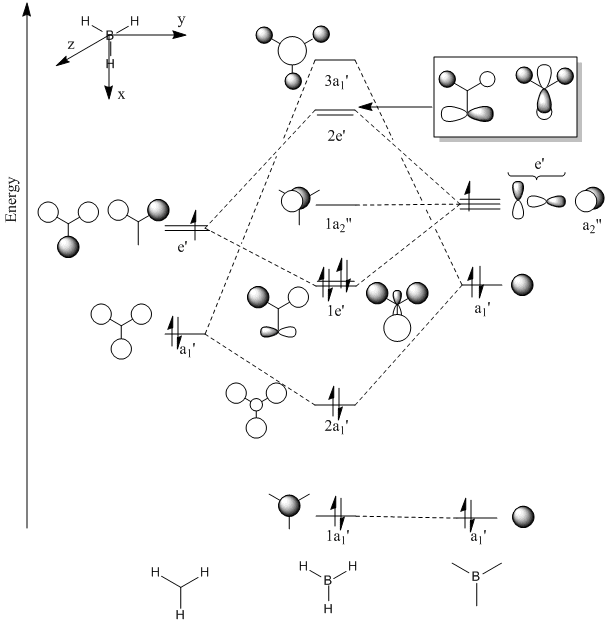
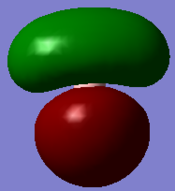
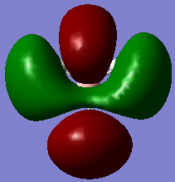
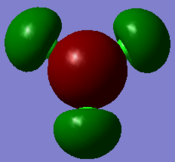
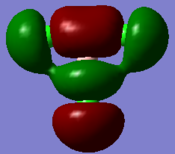
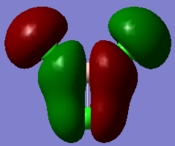
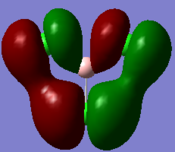
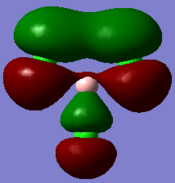
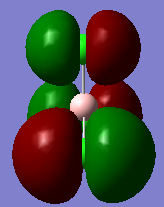
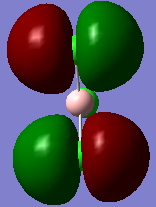
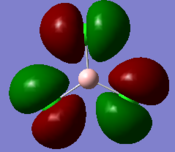
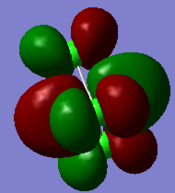
Molecular orbitals and their energies calaculated using Gaussian via SCAN with the DFT/B3LYP method, 6-31G basis set and considering natural bond orbitals. Figure 5 shows the molecular orbital diagram and for BH3 and also the calculated energy for each MO.

MO diagram Calculated energies

Figure 5

Figure 6 shows the eight lowest energy MO's graphically represented after being obtained from Gaussian.

1a1' 2a1' 1e' 1e'
1a2" 2e 2e 3a1'

Figure 6

The 1s orbital of boron is two low in energy at -6.73 Hartree to interact with the 1s orbitals of the hydrogen atoms. The calculated energies provide the evidence that the two MO's with symmetry 1e' and the two MO's with symmetry 2e' are degenerate as shown in the MO diagram of BH3 in figure 5. The MO diagram was produced before the Gaussian calculation so it was unknown whether the 2e orbitals would be higher or lower in energy than the 3a1'orbital; the calculation shows that the diagram is correct in placing the 3a1' higher in energy than 2e. All of the MO's drawn on the diagram are proven to be very similar to the real MO's as calculated by Gaussian.

Natural bond orbital (NBO) results for BH3

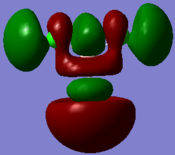
Gaussian used to calculated the NBO to obtain the charge distribution of the BH3 molecule shown below in figure 7 (green corresponds to positive and red corresponds to negative) and the information in table 2 is for the NBO of the BH3 molecule.

Figure 7 Table 2

Figure 7 shows the boron atom being electron deficient, a Lewis acid, and the the hydrogen atoms being relatively electron rich. Boron is a Lewis acid as the B in BH3 is sp2 hybridized and is bonded to three hydrogen 1s orbitals, causing the pz orbital on boron empty and as it is low in energy it will be able to accept a pair of electrons therefore acting as a Lewis acid.

A summary of the bonding in BH3 in shown in figure 8

Figure 8

The bonding summary shows the boron contributes 66.67% from a p orbital and 33.33% from a s orbital this confirms the sp2 hybridization; boron contributes 45.36% to each B-H bond and hydrogen contributes 54.64%.

From table 2 it can be seen that the boron atom has a natural positive charge of 0.27816 and each hydrogen atom has a natural negative charge of 0.09272; the difference in natural charge is due to the distribution of electrons. BH3 carries no overall charge as it is a neutral molecule as the positive boron charge is canceled out by the negative charge from all three hydrogen atome (3 x 0.09272 = 0.27816).

Dspace for BH3 MO's and NBO- DOI:10042/to-10543

TlBr3

Optimization

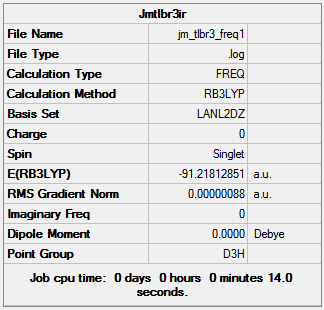
TlBr3 is much larger than BH3 and with 143 more electrons so pseudopotentials are required, which mainly concentrates on the valence electrons where the chemical bond is produced. The TlBr3 is optimized using the B3LYP method and LanL2DZ basis set on Gaussview 5.0.9 after being locked into the D 3h point group to avoid the same mistake shown for BH3. The resultant Tl-Br bond length is 2.65Å which is relatively close to the literature value of 2.52Å[1] and the Br-Tl-Br bond angle is 120o. Figure 9 shows the results summary from the optimization.

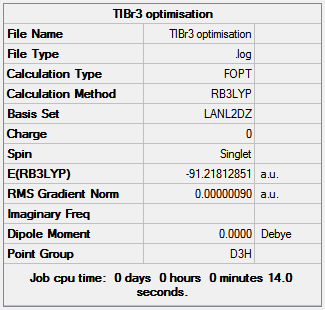
Figure 9
Summary of TlBr3 optimization

The final energy of the molecule is -91.22 Hartree, the RMS gradient is very close to zero (0.0000009) indicating the optimization has finished and the total time of the optimization is 14 seconds, a small amount of time was to be expected as the molecule is very simple. TlBr3 does not poses a dipole due to the D3h point group and means that all bromine atoms have the same orientation to the thallium; D3h point group retained after the optimization calculation as expected.

Figure 10 shows two graphs, the top graph is for the total energy through the optimization and the bottom graph is for the RMS gradient through the optimization for TlBr3.

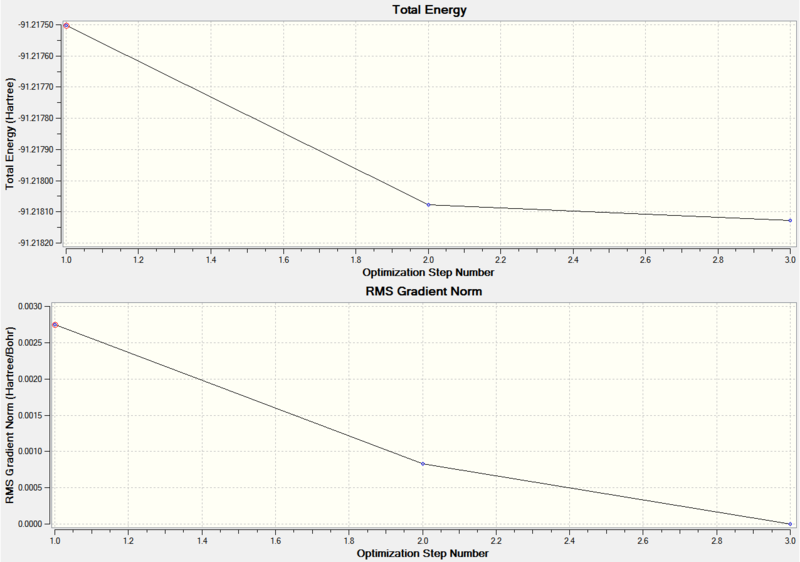
Figure 10
Graphs for TlBr3 optimization

The analysis of these graphs is the same as the as the analysis shown for the BH3 graph analysis at the end of section 1.1; except the optimization is carried out in three steps for TlBr3 and four steps for BH3.

IR spectrum analysis

Gaussview 5.0.9 used to obtain an IR spectrum with the B3LYP method and 3-21G basis set; this is necessary for the same reasons as stated for BH3 at the start of section 1.2. The summary of the IR spectrum calculation is shown in figure 11.

Figure 11

Summary for TlBr3 IR frequency

The total energy is the same as the optimized molecule, -91.22 Hartree and there is no change in the point group of TlBr3; so there is no change from the optimized TlBr3. Figure 12 shows the obtained IR spectrum and table 3 shows the calculated IR spectrum data both for TlBr3.

Figure 12
IR spectrum


No Stretch Wavenumber (cm-1) Intensity Symmetry (D3h)
1 Scissoring 46 3.7 E'
2 Rocking 46 3.7 E'
3 Wagging 52 5.8 A2"
4 Symmetrical stretching 165 0 A1'
5 Antisymmetrical stretching 211 25.5 E'
6 Antisymmetrical stretching 211 25.5 E'

Table 3

The IR spectrum shows three peaks even though Gaussview calculated six vibrational frequencies for the TlBr3 molecule, the same result was shown for the BH3 molecule. The first reason for this is the degree of degeneracy between vibrations one & two and five & six (shown in table 2), the degeneracy causes the peaks to be superimposed over one and other so double each peaks intensity. The second reason is that vibration four has an intensity of zero due to the vibration not having a change in dipole moment as it is perfectly symmetrical. Considering these reasons the IR spectrum produced appears to correspond to the calculation results.

The smaller peaks in the TlBr3 IR spectrum compared to the BH3 IR spectrum is due to the bromine atoms being much larger than the hydrogen atoms therefore will oscillate at a much lower frequency.

What is a bond?

A bond can be said to be an attractive force between atoms, allowing the formation of molecules or crystals via the "sharing" of valance electrons on each atom. Areas of electron density on each atom are known as orbitals and the formation of bonds is due to orbitals of the same symmetry overlapping to share the electron density and stabilize the atoms involved.

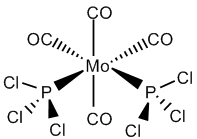
Investigation into Isomers of Mo(CO)4L2

Mo(CO)4(PCl3)2 is optimized using Gaussian through SCAN with B3LYP method and the basis set LANL2MB for the first optimization and LANL2DZ basis set for the second optimization; this is carried out for both the cis and trans isomers of Mo(CO)4(PCl3)2. The LANL2MB basis set is used to optimize the low level pseudo potential and the LANL2DZ basis set increases electronic convergence.

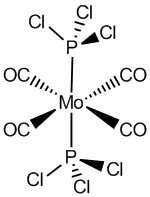
Trans Mo(CO)4(PCl3)2

The structure of the trans isomer as well as the view along the P-Mo bond is shown in figure 13.

Figure 13

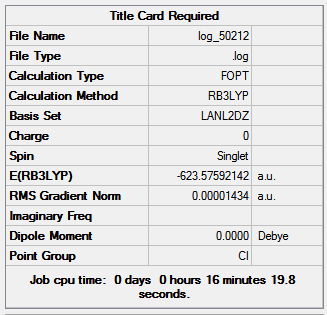
Figure 14 shows the optimization summaries for the trans isomer with basis sets LANL2MB and LANL2DZ.

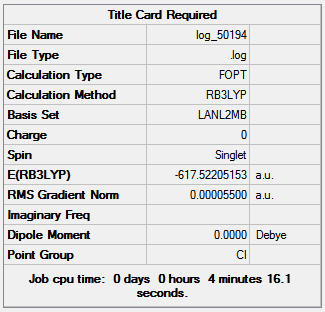
1st optimization 2nd optimization
DOI:10042/to-10600 DOI:10042/to-10608

Figure 14

Table 4 shows the bond lengths and angles of the trans isomer.

Bond Length(Å) 1st optimization Angle (o) 1st optimization Length(Å) 2nd optimization Angle (o) 2nd optimization
P-Cl 2.40 N/A 2.24 N/A
Mo-C 2.11 N/A 2.06 N/A
Mo-P 2.48 N/A 2.45 N/A
C-O 1.19 N/A 1.17 N/A
P-Mo-C N/A 89.4 N/A 89.1
C-Mo-C N/A 179.2 (trans), 90.1 (cis) N/A 180 (trans), 90.0 (cis)
Cl-P-Mo N/A 120.3 N/A 116.5

Table 4

The second optimization is slightly lower in energy than the first; both summarizes show no dipole moment for the trans Mo(CO)4(PCl3)2 and the low RMS gradient indicates that both optimizations are complete. The bond angles are close to the expected values the small discrepancies are due to the inaccuracies of Gaussian. Expected values are: 90o for P-Mo-Co, 120o for Cl-P-Mo, 180o and 90o for C-Mo-C.

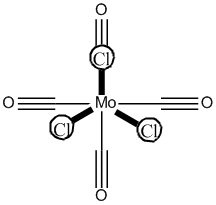
Cis Mo(CO)4(PCl3)2

The structure of the cis isomer is shown in figure 15.

Figure 15

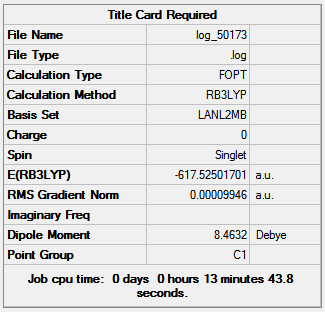
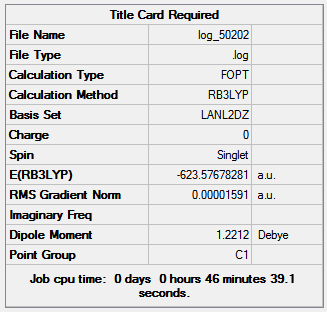
Figure 16 shows the optimization summaries for the cis isomer with basis sets LANL2MB and LANL2DZ.

1st optimization 2nd optimization
DOI:10042/to-10542 DOI:10042/to-10607

Figure 16


Table 5 shows the bond lengths and angles of the cis isomer.

Bond Length(Å) 1st optimization Angle (o) 1st optimization Length(Å) 2nd optimization Angle (o) 2nd optimization
P-Cl 2.39 N/A 2.24 N/A
Mo-C 2.11 N/A 2.06 N/A
Mo-P 2.53 N/A 2.51 N/A
C-O 1.19 N/A 1.17 N/A
P-Mo-Cl N/A 127.4 N/A 123.5
C-Mo-C N/A 89.5 (cis), 178.4 (trans) N/A 89.2 (cis), 178.3 (trans)
P-Mo-C N/A 90.5 (cis), 174.8 (trans) N/A 90.7 (cis), 174.4 (trans)

Table 5


The second optimization is lower in energy than the first; both summarizes show a dipole moment for the trans Mo(CO)4(PCl3)2, with the second optimization producing a dipole moment 7.24 Debye smaller than the first and the low RMS gradient indicates that both optimizations are complete. The bond angles are close to the expected values the small discrepancies are due to the inaccuracies of Gaussian. Expected values are: 120o for Cl-P-Mo, 180o and 90o for C-Mo-C and P-Mo-C.


The cis isomer is shown to be the more stable isomer by 2.23 kJmol-1, this low difference in energy means the two isomers are in equilibrium at relatively low temperatures. The trans isomer is less stable due to experiencing the trans effect which causes destabilization. If more bulky ligands replaced PCl3 e.g. PPh3, the cis isomer could become the more unstable isomer due to steric effects of the new ligands.

To gain more accurate results a higher basis set could be used, such as 6-311G(d,p).

After the optimizations of both isomers Gaussview 5.0.9 does not show "bonds" between Mo and P, P and Cl; this is due to the "bond" distance being out of the range of Gaussview's internal list of bond distances. A bond is an undefined concept as it is not fully explained by distance, energy nor electron density.

IR Analysis of Mo(CO)4(PCl3)2

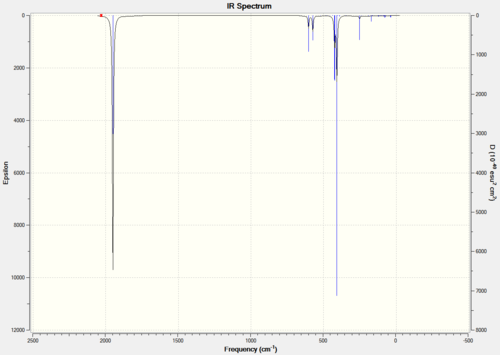
IR spectra obtained for the both cis and trans isomers using Gaussian through SCAN with B3LYP method and the basis set LANL2DZ. The spectra are used to investigate the differences in vibrational frequencies, particularly those of the CO ligands. Table 6 shows the spectra for the cis and trans isomers and a magnification of the CO vibrational region.

Cis Isomer Trans Isomer
DOI:10042/to-10628 DOI:10042/to-10629

Table 6

Table 7 shows the vibrational frequencies for the CO ligands for both isomers.

Number Wavenumber (cm-1)
Cis isomer 1 1945
2 1949
3 1958
4 2024
Trans isomer 1 1950
2 1950
3 1977
4 2031

Table 7

There are four vibrations shown for each isomer although there are two degenerate peaks for the trans isomer and are of very low intensity. The large difference in frequency for vibrations 3 and 4 for the cis isomer is due to the two CO ligands being in different environments; one equatorial and one axial. A low basis set means there is inaccuracies in the calculation, shown in the lack of degeneracy of the vibrations as one peak is expected for the trans isomer and two peaks for the cis isomer.

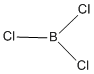
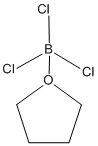
Mini Project: Investigating the effects of a donor solvent THF on BCl3

The aim of the mini project is to investigate the difference in energy and vibrational frequencies between optimized structures of boron trichloride and boron trichloride tetrahydrofuran adduct; also to produce and analyze a molecular orbital diagram and NBO for boron trichloride. Figure 17 shows the structures of the models being investigated; BCl3 on the left and the THF BCl3 adduct on the right.

Figure 17

Optimization of BCl3

The boron trichloride molecule is optimized using Gaussian through SCAN with a pseudopotential due to the large number of electrons on the model from the three chlorine atoms; using B3LYP method and LanL2DZ basis set. The B-Cl bond length and Cl-B-Cl angle were found to be 1.79 Å and 120o respectively. Figure 18 shows the results summary for the optimization.

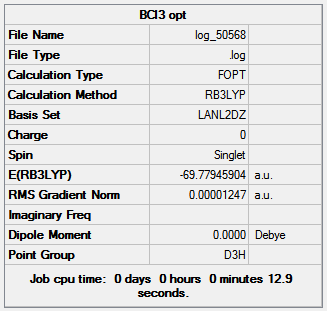
DOI:10042/to-10701
Figure 18

The very low RMS gradient is indicates that the optimization is complete. There is no dipole moment as the molecule is trigonal planar with all the polar B-Cl bonds being symmetrical therefore canceling one and other out to give an overall neutral molecule; the D3h point group means that all chlorine atoms have the same orientation to the boron. The energy of BCl3 is lower in energy than BH3 calculated earlier due to the stronger B-Cl bonds which are however longer than the B-H bonds due to the larger atomic size of chlorine compared to hydrogen.

Molecular orbital results for BCl3

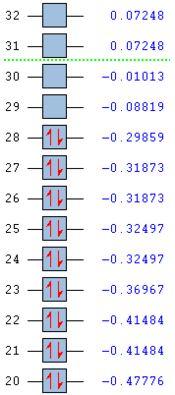
Molecular orbitals and their energies calculated using Gaussian via SCAN with the DFT/B3LYP method, 6-311G(d,p) basis set and considering natural bond orbitals. Figure 19 shows the MO's 20-31 graphically represented after being obtained from Gaussian and the energy of these orbitals.

Energy level 20 Energy level 21 Energy level 22 Energy level 23
Energy level 24 Energy level 25 Energy level 26 Energy level 27
Energy level 28 (HOMO) Energy level 29 (LUMO) Energy level 30 Energy level 31

Figure 19

Molecular orbitals below the energy of -0.47776 Hartree are not shown here as they are deemed too low in energy and too for from the HOMO LUMO region to be important. The calculated energies show degeneracy between molecular orbitals 21&22, 24&25, 26&27 and 31&32. The HOMO can be seen to have three nodal planes and the LUMO can be seen to have four nodal planes this causes the LUMO to be higher in energy. The LUMO has a negative energy which indicates it is a bonding orbital. The low lying means that BCl3 is an electrophile being able to accept electrons into the LUMO via nucleophilic attack; this is illustrated with tetrahydrofuran. The molecular orbitals are not occupied close to or past the zero energy point therefore no antibonding orbitals are occupied so the molecule is relatively stable.

Natural bond orbital results for BCl3

Gaussian through SCAN used to calculated the NBO to obtain the charge distribution of the BCl3 molecule shown below in figure 20 (green corresponds to positive and red corresponds to negative) and the information in table 8 is for the NBO of the BCl3 molecule.

Figure 20 Table 8

It can be seen from figure 20 that boron is electron deficient and chlorine atoms are electron rich, this is due chlorine being more electronegative than boron therefore has a greater "pull" on the electrons in the B-Cl bond. The boron center has six valence electrons so is considered electron deficient in terms of the octet rule so boron trichloride will dimerize to become more stable; the electron deficiency of boron also accounts for the Lewis acid behavior of BCl3.

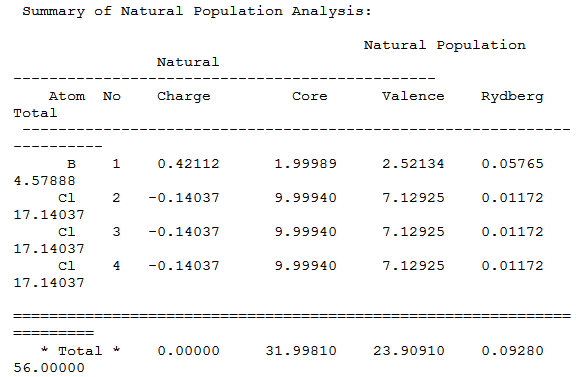
The boron atom is sp2 hybridized as each B-Cl bond consists of a 66.46% contribution for a p orbital, 33.28% contribution for a s orbital and a small 0.25% contribution for a d orbital; boron contributes 31.71% to each B-Cl bond and chlorine contributes 68.29%. Table 8 shows boron with a positive charge of 0.42112 and each chlorine atom with a negative charge of 0.14037; there is no overall charge on BCl3 as 3 x -0.14037 = 0.42111. The remaining positive charge of 0.00001 is down to inaccuracies of Gaussian.

Dspace for BCl3 MO's and NBO-DOI:10042/to-10705

Optimization of THF

Tetrahydrofuran molecule is optimized using Gaussian through SCAN with the B3LYP method and 6-311G(d,p) basis set. Figure 21 shows the results summary for the optimization and table 9 shows the bond lengths plus angles ( an(O) indicates that one of the carbons in bonded to the oxygen).

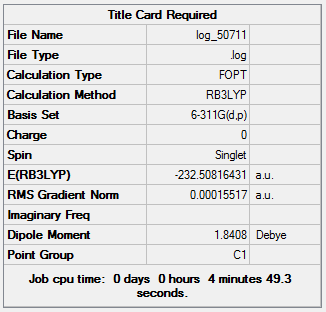
DOI:10042/to-10730
Figure 21


Bond Length/Å Angle o
C-O 1.43 N/A
C-C 1.54 N/A
C-H 1.09 N/A
C-C (O) 1.55 N/A
C-H (O) 1.10 N/A
O-C-C N/A 108.5
C-C-C N/A 105.4
H-C-H N/A 107.7

Table 9

The low RMS gradient indicates the optimization is complete. There is a dipole present due to the electronegative oxygen atom having a greater affinity for the electrons in the C-O bond than carbon, producing two slightly positive carbon atoms and a slightly negative oxygen atom. THF is shown to have a much lower energy than BCl3 as it is a lot more stable due to all the atoms, except hydrogen, having a full valence octet of electrons compared to the electron deficient boron. Also the C-O and C-C bonds are stronger than the B-Cl bonds.

Optimization of the BCl3 THF adduct

The boron trichloride tetrahydrofuran adduct is optimized using Gaussian through SCAN with a pseudopotential due to the large number of electrons on the model from the three chlorine atoms; using B3LYP method and LanL2DZ basis set. The bond lengths of the adduct are as follows, B-O 1.58 Å, B-Cl 1.88 Å and C-O 1.52 Å; the Cl-B-O and Cl-B-Cl bond angles for the adduct are 106.7o and 112.4o respectively. Figure 22 shows the results summary for the optimization.

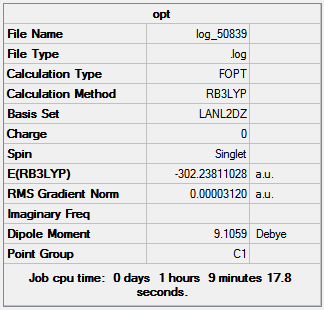
DOI:10042/to-10825
Figure 22

The low RMS gradient indicates the optimization is complete. There is a much larger dipole present in the adduct than THF and BCl3 combined due to the chlorine atoms no longer canceling one and other out as the boron is now almost a tetrahedral structure not triginal planar. This is also reflected in the change of Cl-B-Cl bond angle going from 120.0o to 112.3o, indicating the boron is no longer sp2 hybridized and now sp3.

The energy of the adduct is -302.238, lower than both THF and BCl3. The energy of formation calculation is shown in table 10.

ΔE = E(adduct) - [E(THF) + E(BCl3)]
ΔE = -302.23(adduct) - [-232.508(THF) + -69.779(BCl3)]
ΔE = 0.049 Hartree
ΔE = 128.6 kJmol-1
Table 10

The formation of the adduct requires a relatively small energy input as for the THF to become close enough to the positive boron it needs to distort the BCl3molecule. The distortion involves the repulsion of chlorine atoms to one side ot the BCl3 molecule causing an increase in bond length and a decrease in bond angle[2]; this explains the difference in B-Cl bond length and Cl-B-Cl between the adduct and the BCl3 molecule. The energy required to preform the distortion combined with energy lost from the weakening of the B-Cl and O-C bonds is greater that the energy gained from the formation of the B-O bond, this is why the an input of energy is required to produce the adduct.

IR spectra analysis of BCl3 and the BCl3 THF adduct

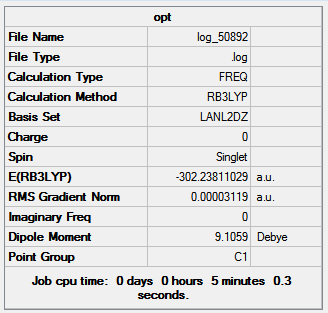
Gaussian through SCAN used to obtian IR spectra for BCl3 and the BCl3 THF adduct with B3LYP method and LanL2DZ basis set to determine the change in vibrational frequencies when boron has a full valence octet of electrons. The the results summary for both spectra is shown in figure 23.

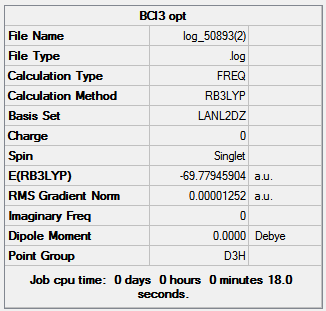
BCl3 Adduct
DOI:10042/to-10872 DOI:10042/to-10870

Figure 23

There is no change in the energy, dipoles and point group between the optimized molecules and the vibrational calculations of the molecules. Both summaries show a low RMS gradient which indicates the vibrational calculations for both are complete.

Table 11 shows the IR spectra for the adduct and BCl3.

BCl3 Adduct

Table 11

Table 12 shows the vibrational frequencies for BCl3 the relevant frequencies for BCl3THF adduct.

Molecule Number Wavenumber (cm-1) Intensity
BCl3 1 247 1.7
2 247 1.7
3 427 0.0
4 433 10.9
5 895 378.1
6 895 378.1
BCl3THF adduct 1 208 2.4
2 212 3.8
3 338 1.5
4 370 0.5
5 730 86.8
6 753 126.1

Table 12

There is degeneracy in the BCl3 spectrum between peaks 1&2 and 5&6 this is not seen in the adduct spectrum. Changes in intensity of some of the peaks is due to the coordination of THF causing distortion of the BCl3 structure, leading to the dipole moment being different in the adduct therefore altering the intensity of the peaks. The distortion caused by the THF coordination leads to the Cl-B bond increasing in length thus becoming weaker; this is why the vibrational frequencies of bonds in the adduct are lower than in BCl3.

Optimization of BF3 and a BF3 THF adduct

In this section fluorine is used is place o chlorine to investigate the effect this will have on energy of formation of the THF adduct. Optimizations for both are carried out using Gaussian through SCAN with the B3LYP method and LanL2DZ basis set. The B-F bond length and F-B-F are found to be 1.35 Å and 120.0o respectively; bond lengths for the adduct are as follows: B-O 3.40 Å, B-F1.36 Å AND C-O 1.48 Å, the Cl-B-Cl found to be 118.4o. Figure 24 shows the results summary for both the BF3 optimization and the BF3 THF adduct optimization.

BF3 BF3 THF adduct
DOI:10042/to-10948 DOI:10042/to-10950

Figure 24

Both summaries show very low RMS gradients indicating both optimizations are complete. The dipole present in the adduct is lower than the dipole for the BCl3 THF adduct as the THF has less impact on changing the triginal planar structure of BF3. The energy of the adduct is -556.975, a lot lower than both THF and BF3. The energy of formation calculation is shown in table 13.

ΔE = E(adduct) - [E(THF) + E(BF3)]
ΔE = -556.975(adduct) - [-232.508(THF) + -324.554(BF3)]
ΔE = 0.087 Hartree
ΔE = 228.4 kJmol-1
Table 10

There is a higher formation energy for the BF3 THF adduct compared to the BCl3 THF adduct by 0.038 Hartree (99.8 kJmol-1). This is due to the B-F bonds being shorter and therefore stronger than the B-Cl bonds, the higher strength bond means that a larger amount of energy is need to stretch the B-F bond so the distortion of BF3 requires more energy as the fluorine atoms are not as easily repelled. This is reflected in the bond angles and bond lengths in the BF3 THF adduct as their change is minimal compared to the changes seen in the BCl3 THF adduct.

The B-F bonds are stronger because orbitals used in the bond from fluorine are less diffuse than those from chlorine, so produce better orbital-orbital overlap. Boron trichloride can be said to be more Lewis acidic than boron trifluoride as it can coordinate a pair of electrons from a donor molecule more easily than boron trifluoride.

Conclusion

Overall I feel the project has been a success with only a few minor problems with SCAN. It can be concluded that the Lewis acidity of a molecule is directly proportional to the ease at which the molecule can be distorted. Also that generally speaking cis isomers of octahedral metal complexes are more stable than the trans isomer due to the trans effect.

References

  1. ↑ J. Blixt et al, Structure of thallium(III) chloride, bromide, and cyanide complexes in aqueous solution
  2. ↑ Bryan D. Rowsell, Ronald J. Gillespie, and George L. Heard, Inorg. Chem. 1999, 38, 4659-4662
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:joewikiwiki&oldid=819794"