Rep:Mod:joc12

                           Year 3 Core Computational Physical - Transition States and Reactivity
                                        Name: Joshua Carr CID: 00731400

Part 1: Cope Rearrangement Tutorial

Background

The Cope Rearrangement is a pericyclic process whose mechanism that has been widely studied. It is a [3,3] sigmatropic rearrangement of a diene possessing terminal alkenes. 6π electrons participate in this reaction and has a suprafacial component. The Transition State has Huckel topology. Using Gaussian, this reaction was investigated. 1,5 hexadiene is an alkene that can undergo the Cope Rearrangement.

Figure 1: Cope Rearrangement through a concerted pericycle mechanism.

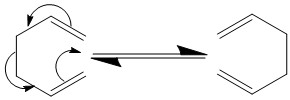
Optimizing the Reactants and Products

Lowest Energy Conformation The central four carbons of 1,5 hexadiene can adopt two different conformation type: anti and gauche. The anti conformation refers to the dihedral angle of the hydrogens on the carbon backbone being 180 ^o. There is a stabilization effect caused by the favorable overlap of the C-H σ and the C-H σ^* orbital. The gauche conformation has the hydrogens between Carbon 3 and Carbon 4 possess a dihedral angle of 60^o.

The preferred confirmation will depend on the following factors:
1) The strength of the orbital overlap between C-H σ and the C-H σ^* orbital.
2) The extent of Pauli replusion between C-H σ and the C-H σ. This refers to bond electron repulsion and is a destabilizing effect.
3) The Van der Waals dispersion forces in between non-bonded atoms. This can be either an stabilizing or destabilizing effect.

To investigate the structure, 1,5 hexadiene was optimized using Gaussian at a HF/3-21G level of theory. The Figure 1 below shows the results of the optimization displaying their energy and point group.

Anti Conformation			Gauche Conformation
Image	Energy (Hartree-Fock Units)	Point Group	Image	Energy (Hartree-Fock Units)	Point Group
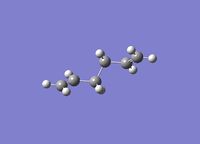
	-231.6926	C2		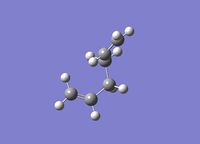-231.6896	C1

The Anti structure corresponds to Structure 1 in Appendix 1 and the Gauche structure corresponds to Structure 5 in Appendix 1. From these results, it can be inferred that the anti confirmation is more energetically favourable than gauche confirmation. To test this hypothesis, a structure was optimized again without any of the dihedral angles set. These obtained structure is a gauche conformer as shown by the dihedral angles being 180^o. This structure corresponds to Gauche structure 6 in Appendix 1. This is an anti conformation which matches the theory.

Figure 2: Optimized Guess Structure

The gauche is preferred because the stabilization to possesses less repulsive forces than the anti conformation does though the difference is minimal.. Gauche is usually adopted by alkanes because it minimizes the Pauli Repulsion which is more important the C-H σ and the C-H σ^* orbital stabilisation. This is due to C-H being a high energy donor and high energy acceptor making the effect negligible.

The C_i point group is the point group of the Anti-2 structure in Appendix 1. This particular structure has the dihedral angles of the hydrogens at 180^o as well as fixing the rest of the hydrogen on the same horizontal plane possess a dihedral angle of 60^o It has an energy of -231.69254 au. A optimization was performed to compare the outputs using the HF/3-21G level of theory in Gaussian.

HF/3-21G vs. DFT/6-31G*

This structure was optimized using a higher level of theory: B3LYP/6-31G* as well as setting the Density Functional Theory (DFT) method.

Ci HF/3-21G level of theory	Ci B3LYP/6-31G* level of theory
Energy (Hartree-Fock Units)	Energy (Hartree-Fock Units)
-231.461346	-234.408998

Once the calculation was completed, the structure produced was almost identical to the input file. However, there was an energy change. The new energy was lower. This shows that the higher level theory was produced a structure that possesses a lower energy minima.

Density Functional Theory is a higher level theory in comparison to Hartree-Fock. Hartree-Fock is better suited for atomic systems consisting of < 5 whilst Density Functional Theory is better equipped is deal with > 5-10 atomic systems with greater accuracy. DFT is based off the electron density distribution n(r) instead of many-electron wave functions that Hartree-Fock is based off.The basis for DFT comes from Hohenberg and Kohn who stated that the Specification of the ground state density n(r) determines the external potential υ (r). The key difference the Hartree-Fock and DFT is the that DFT takes into account the exchange correlation energy which is also known as the Pauli Repulsion derived from the Pauli Exclusion Principle. Taking this effect into account, DFT makes more apt approximations compared to Hartree-Fock revealing more energy stabilisation effects hence a lower energy. 6-31G is also more precise than 3-21G. The 6 means that d and f orbitals are taken into account instead of just s and p. /

In order to determine the vibrational energies of the bonds, a frequency optimization had to be undertaken. The B3LYP/6-31G* optimized structure was subjected to a frequency calculation. This was done to obtain show the vibrations the molecule undergoes as well as producing an Infra-Red spectrum. After the optimization, no imaginary frequencies were produced.

Figure 3 is the Vibration Movie of the C_i Hexadiene

Figure 4 is the IR generated from the calculation of the C_i Hexadiene

Energies of the C_i Structure

In addition to these, a variety of electronic and vibrational energies were calculated in Hartrees. An attempt to calculate these values at 0 K was attempted, but was unsuccessful. Thus all 0 K values were calculated using correction values in the Log file.

Ci HF/3-21G level of theory 298.15K				Ci HF/3-21G level of theory 0 K
Sum of Electronic and Zero Point Energies (Hartrees)	Sum of Electronic and Thermal Energies (Hartrees)	Sum of Electronic and Thermal Entahlpies (Hartrees)	Sum of Electronic and Thermal Free Energies (Hartrees)	Sum of Electronic and Zero Point Energies (Hartrees)	Sum of Electronic and Thermal Energies (Hartrees)	Sum of Electronic and Thermal Entahlpies (Hartrees)	Sum of Electronic and Thermal Free Energies (Hartrees)
-231.539539	-231.532565	-231.531621	-231.570915	-231.369254	-231.372595	-231.370707	-231.449295

Ci B3LYP/6-31G* level of theory 298.15K				Ci B3LYP/6-31G* level of theory 0 K
Sum of Electronic and Zero Point Energies (Hartrees)	Sum of Electronic and Thermal Energies (Hartrees)	Sum of Electronic and Thermal Entahlpies (Hartrees)	Sum of Electronic and Thermal Free Energies (Hartrees)	Sum of Electronic and Zero Point Energies (Hartrees)	Sum of Electronic and Thermal Energies (Hartrees)	Sum of Electronic and Thermal Entahlpies (Hartrees)	Sum of Electronic and Thermal Free Energies (Hartrees)
-234.416259	-234.408966	-234.408021	-234.447881	-234.272814	-234.258227	-234.256338	-234.336058

Optimizing the "Chair" and "Boat" Transition Structures

Background

The Cope Rearrangment goes through a Transition State that can either adopt the chair or boat conformations. Both of these conformations are composed two allyl fragments separated at the terminal ends by 2.2 A. The energy of the transition state is important to determine because it represents a maxima in the potential energy surface. The chair conformation is in the C_2h point group. The boat conformation is in the C_2v point group.

The Chair Transition State

Optimizing these transition structures can be done via two different methods. The first method using the TS(Berny methodology) using HF/3-21G level of theory. In order to do this optimization, an estimation of the Transition state must be done. This part of the experiment took a long time. This is due to the estimates of the transition states first conducted were not of sufficient quality to produce an accurate optimized Transition state producing the Lnk1e in C:\G09W\l9999.exe error would occur. The distances had to be set precisely to 2.2 A otherwise he two allyl fragments joining together via C3-C4 respectively. After much testing, the chair transition state was eventually isolated.

Figure 5 above shows the transition state calculated to possess an imaginary vibration of -818 to 3 s.f as well being in the C_2h point group. This indicates that this is indeed a transition state.

Another method of obtaining the transitions state was to freeze the intermolecular distances between the two allyl fragments in the Redundant Co-ordinate Editor in Gaussian. One of these distances represent the bond that formed upon completion of the rearrangement. Freezing the distance to 2.2 A will produce a structure that would be on the potential energy surface for that particular distance. The non-frozen distances will be optimized with respect to that inter molecular separation. Once a structure was obtained for 2.2 A value, the frozen distances were subsequently optimized by altering the conditions in the Redundant Co-ordinate Editor. This was achieved by altering the Freeze Co-ordinate to the Derivative which follows Hessian Methodology.

Berny NoEigen Chair TS			Frozen/Derivative Chair TS
Image	Point Group	Bond Distance between Broken/Made	Image	Point Group	Bond Distance between Broken/Made
	C2h	2.02015		C1	2.02017

The resultant structure looked similar to the structure produced without using the Redundant Co-ordinate Editor. They both had the same point group and by eye, appeared identical. The bond lengths are almost identical with differences arising from numerical approximations of the program. The key difference is symmetry. The NoEigen method produces the correct point group (C_2h), but the second method does not. It can be symmetrized to the C_2h.

In terms of usability, the second method was a lot easier to use. It provided more control over the input structure. Whilst both methods suffers when the input structure was not close enough to the Transition State Structure, the Redundant Co-Ordinate Editor allowed the intermolecular distances being set in the co-ordinate removing a lot of the trial and error the first method suffered from. This reduced the amount of errors in the calculations encountered in the experiment. The second method is also preferable since it is allows the intermolecular distances to be frozen. As a consequence, different structures on the reaction co-ordinate can be easily studied and physical properties can be quickly retrieved.

The Boat Transition State

In order to optimize the boat transition state, a different method was used. The C_i of 1,5 hexadiene optimized structure was taken to be the reactant and product and placed into two separate molecular group windows in the same Gaussian input file . Each structure was labelled and rotated to illustrate a before and after picture. These structures were subject to a TS (QST2) process in a Opt+Freq calculation. Initially, the calculation failed because the two structures entered for optimization could not be linked to a Transition state. This was due to the geometries being incorrect. This job failed to produce a boat transition state. All that it produced was an almost identical structure that still was in the C_i point group. The resulting structure produced was like the chair transition state, but with increasing bond lengths as shown below. It became clear that the anti conformation would form the chair transition state over the boat. Therefore, alterations to the geometry were made. The dihedral angle of the central C-C-C-C backbone was set to 0^o. In addition to this, the C-C-C bond angle was reduced from 109.5^o to 100 ^o.

There was a lot of difficulty in obtaining a optimized Transition state even after these alterations. The link kept crashing due to unforeseen problems. The reason for the error was the same as earlier: Lnk1e in C:\G09W\l9999.exe. An attempt to optimize the pre-structures so it looks the closest to the boat conformation produced an unsuccessful TS transition structure. The same error was given. This failure represents the limitations of the QST2 methods. The structure has to be very close to the transition state in order for the calculation to be successful. The tolerance error appears to be too narrow for estimation. Another source of error were the orientation of the hydrogens being different in the two structures. If a hydrogen was facing out of the plane in the reactant yet the equivalent was pointing into the plane in the product. Further experimentation is needed to find a better method for determining the transition states. Due to time constraints from calculation problems and file glitches, QTS 3 was not chosen for further experimentation. This method involves a third window where the Transition State approximation is placed. This method might be more desirable because it provides Gaussian with more information about the reaction profile.

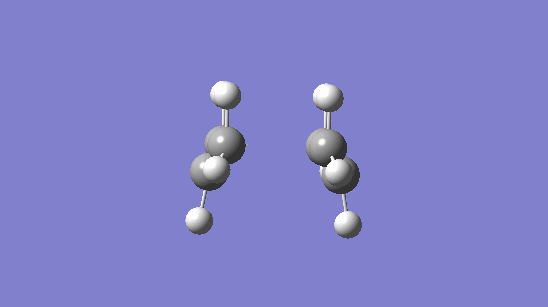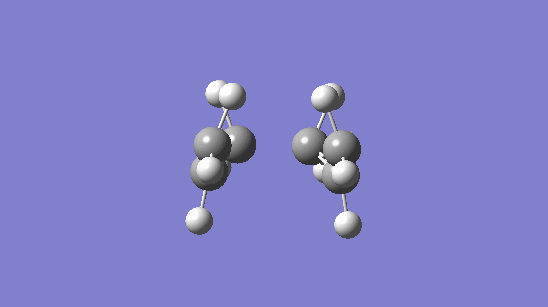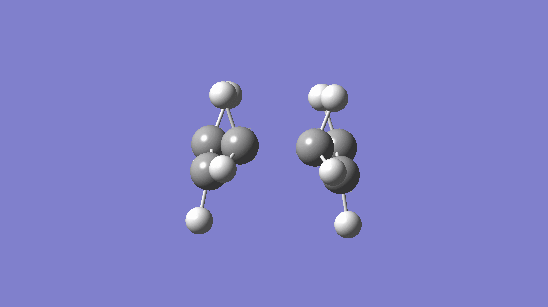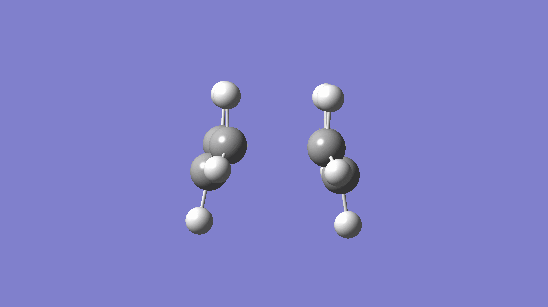
Figure 6 above the Boat vibrates similarly to the Chair indicating that it is indeed the Cope Arrangment. It belongs to the C_2v point group as predicted.

The Intrinsic Reaction Co-ordinate (IRC)

Once the optimized chair and boat transition states were located, it is necessary to see what the reaction co-ordinate of this reaction is. Each conformation will go through a different Transition state because of their geometry. There are three different approaches to find the minimum geometry.
1) Optimize a Minima for the final step produced
2) Calculate Force Constants at every step
3) Use more steps in the reaction co-ordinate.

An IRC was run intially using HF/3-21G where the parameters were: Forward Direction, Force Constant calculated once and 50 steps. This produced a movie where the final step hadn't gone to products. So the three methods were tested:

Method 1: The final step was successfully optimized to a minima which was the hexadiene as expected.
Method 2: Produced more frames, but still insufficient number of frames necessary to complete the IRC.
Method 3: When the number of steps was increased from 50 to 100, the calculation ran to completion meaning that the initial step number was too small.

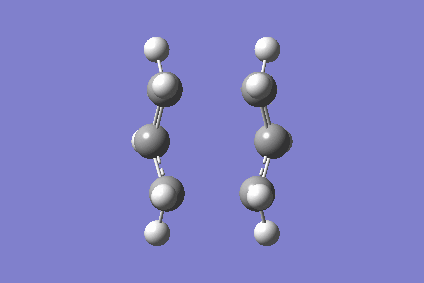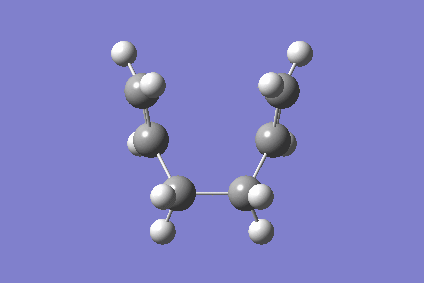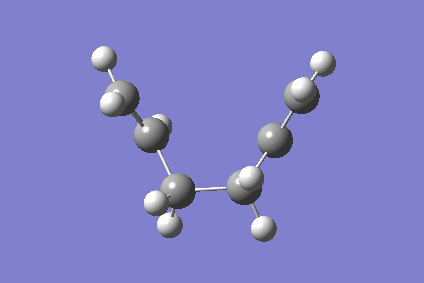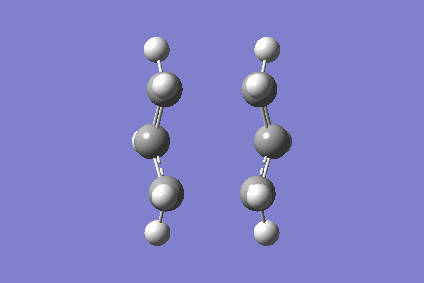
Figure 7 above the movie above is a 78 step IRC calculation that showing the chair TS going to products forming the gauche conformation as shown by the last frame of the movie. It can concluded from this that the boat TS forms the anti conformation. As the Figure 8 depicts below, the chair structure obtained is indeed a transition state and at the peak of the reaction co-ordinate.

Activation Energies for the Cope Rearrangement

In order to determine the activation energy for the Cope Rearrangement via both structures, a higher level of theory is required. B3LYP/6-31G* level of theory optimizations and were carried out. Comparisons to the lower level of theory were carried out also.

Activation energy for the Chair TS (kcal/mol)
HF/3-21G at 298.15 K	HF/3-21G at 0 K	B3LYP/6-31G* at 298.15 K	B3LYP/6-31G* at 0 K	Expt at 0K.
44.69	45.57	35.12	34.01	33 ± 0.5

Activation energy for the Boat TS at 0 K
HF/3-21G at 298.15 K	HF/3-21G at 0 K	B3LYP/6-31G* at 298.15 K	B3LYP/6-31G* at 0 K	Expt at 0K.
54.76	55.78	42.12	43.09	44.7 ± 2.0

Comment: The activation energies have a good agreement with the literature. Differences arise from the approximates in HF and DFT theory.

Part 2: Diels-Alder Reaction Study

Introduction

The Diels-Alder is regioselective pericylic reaction involving a diene and dienophile. The π orbtials from the dienophile must be similar energy level to the π orbitals on the diene. This ends up forming 2 new σ bonds. The reaction works particularly well with electron withdrawing group present on the dienophile such as maleic anhydride. The electron withdrawing group must be conjugated to the double bond in the dienophile. The reaction is permitted when the HOMO and the LUMO of the reactants can achieve significant overlap destiny. The diene has to be in the s-cis conformation. The Diels-Alder adduct can adopt the endo or the exo product. The preference of formation is dependent on the reaction conditions.

Cis-Butadiene and Ethylene Diels Alder - Analysis of the Nature of Diels Alder reactions

The most basic Diels Alder reaction is between an ethene and cis-butadiene. This reaction produces cyclohexene. The transition state formed is an envelope shape either endo or exo optimized by the π orbitals from the ethane overlapping with the π system of the cis-butadiene. Cis-butadiene was optimized so that the HOMO and LUMO could be obtained in Gaussian.

Semi Empirical Methods vs Hartree Fock

AM1 Semi Empirical is a method that takes Hartree Fock and sets certain approximations to zero and adds parameters to fit in with experimental data./. Attempts were made to get the structures using Hartree Fock and DFT, but they were unsuccessful.

MOs of reactants

Cis-Butadiene HOMO			Cis-Butadiene LUMO
Image	Symmetry with respect to the vertical plane	Energy	Image	Symmetry with respect to the vertical plane	Energy
	Anti - Symmetric	-0.34381		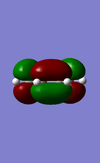Symmetric	0.01707

Ethylene HOMO			Ethylene LUMO
Image	Symmetry with respect to the plane	Energy	Image	Symmetry with respect to the plane	Energy
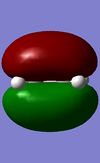
	Symmetric	-0.26746		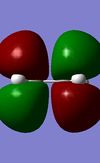Anti - Symmetric	0.01742

These HOMO and LUMOs would be compared to that of the transition state.

Transition State Calculations and MO Analysis

The transition state estimate was obtained by drawing using a bi-cyclo system and adapting it accordingly. The transition state was obtained by the QTS 2 method after the freezing/derivative method failed to produce a transition using AM1 semi-empirical methods. Physical data such as vibrations and energies were obtained. An IRC calculation was attempted, but there wasn't successful.

The HOMO and LUMO of the Transition State were found as well as shown below:

Diels Alder TS HOMO			Diels Alder TS LUMO
Image	Symmetry with respect to the plane	Energy	Image	Symmetry with respect to the plane	Energy
	Symmetric	-0.30086		Symmetric	0.14244

A typical sp³ C-C bond length is 1.54 nm and sp² C-C bond length is 1.39 nm respectively. The Van der Waals radii of Carbon is 1.70 A. Taking these number. The bond forming distance in the optimized Transition State is 2.20 A and the carbon bonds involvement in the concerted electron pushing are 1.37. These values indicate delocalisation of electrons. The value is close to that of benezne which is 1.40 A indicating aromatic like stabilization which is in accordance with Huckel topology this reaction follows. Transition State Geometry - C_¹ where it could easily be symmetrized to C_s. The C_s geometry is likely to be the transition state geometry meaning the structure produced is not the true transition state, but rather a structure on with large relative positive position on the potential energy surface.

Vibration of Transition State and lowest positive frequency.
Figure 9 below shows the Imaginary vibration of this particular structure vibrating at -818 cm^-1.

Figure 10 below shows the real vibration of this particular structure vibrating at 166 cm^-1.

Explanation of HOMO and LUMO

Figure 10: MO diagram of forming TS MOs

The reason for the choices made in this diagram were as follows: 1) Orbitals only interact with those with those of the same symmetry. 2) The LUMO of the diene and the HOMO of the dienophile are closer in energy hence they have the greatest splitting. As a result, this is what causes the LUMO. As a result of this, means that the bonding MO is lower than the reverse molecular interaction. The HOMO is higher in energy than the equvialent to the cis-butadiene since it is in a transition state.
Synchronicity

If the bond formation is synchronous, then the bonds formed at the same time. Conversely, if bond formation is asynchronous then the bonds do not form at the same time. There is some controversy as to whether Diels Alder is synchronous or not. In theory, a a pericycle reaction such as this should be synchronous, but there is an opposing theory that bond formation is actually asynchronous. A method of determining this is whether the both intermolecular distances between the termini of the diene and dienophile are the same. As seen by the transition state geometry and the data extracted. It is clear that this Diels Alder is synchronous due to the very similar numerical quantities. Differences arise from the numerical approximations done in the calculation itself.

Structure II During another computation, structure was computed and it is very similar to the typical drawings for a transition state.

Figure 11 below shows the imaginary frequency below with the frequency of -54 cm^-1.

Figure 12 below shows the real frequency below with the frequency of 156 cm^-1.

This structure is probably on the other side of the potential energy surface since the IRC calculation produced taken was only eleven steps frames and it is difficult to see a change in the bonds.

Why is reaction allowed?

The List Below is the selection rules:

1)The reaction is allowed because it follows the selection rules:
2)If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed. The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden.

If one was to compare the HOMO and LUMOs of the reactant, it is clear that there is energy matching because they similar in symmetry. Since they are similar in energy, there is significant overlap destiny. This means that the reaction is thermodynamically feasible. However, it does not take into account kinetics.

Regioselectivity - Exo vs Endo Products

Introduction

Diels Alder reactions are regioselective. The exo and endo compete with each other. What differentiates them is a balance between steric and secondary orbital effects. Intrinisically, the endo is favoured to form first because it has the lesser sterics and has these orbital overlap effects. To test this theory, Cyclohexadiene and Maleic Anhydride were chosen as reactants for a Diels Alder cycloaddition and observe what occurs at the Transition State with the bond distances and HOMOs.

The Exo Transition State Calculation

Exo Transition State was found by using the TS (QTS2) method by first optimizing the exo product semi-empirically. This product was copied to the first window where it was altered back into the reactants. This process was surprisingly swift in obtaining a reasonable estimate for the transition state. Once the reactants were cleaned, the optimization was run producing the vibrating Transition State and the IR. The Endo Transition state was much harder to optimize. The QTS2 was initially unsuccessful in producing the correct structure. It produce a structure that possessed four imaginary stretches two of which were over 1000 cm^-1. This was despite looking almost like the perfect transition state. A common error was Lnk1e in C:\G09W\502.exe error indicating there was a convergence failure indicating there is a very flat potential surface. Hartree-Fock methodology was then applied instead of semi-empirically producing and failed for similar reasons. The Freeze Co-ordinate and Derivative Hessian method was also tested. The bond lengths were set to around 2.3 A before the calculation was. Semi-empirical methods failed to achieve the transition state. HF and DFT were then tested and the results of these were unsuccessful. Eventually, a reversion back to the QTS2 and setting the intermolecular distances to around 2.3 A managed to achieve the Transition State required.

Results and Discussion

Figure 13: Sketch of Endo TS obtained

Figure 14: Sketch of Exo TS obtained

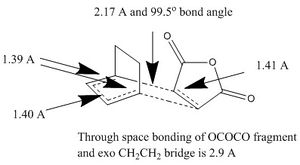
These structures were very close to the transition state though there are reasons as to why they are not. The C-C bond distances of the already made bonds that follow Huckel topology aren't the same distance. They are very close, but they aren't the same. They should be 1.39 A. The differences arise could be found a slightly incorrect angle of approach or limitations in the semi-empirical methods used. Further experimentation and calculations are needed to verify the cause.

Vibrations

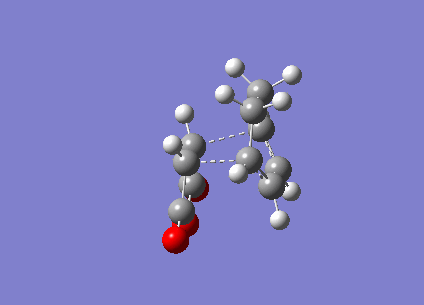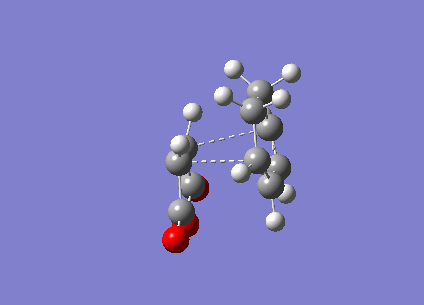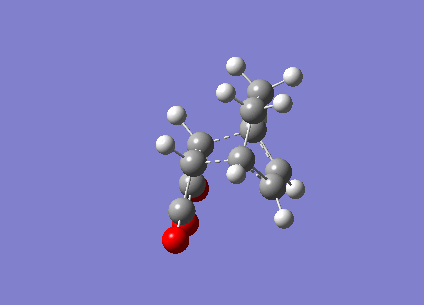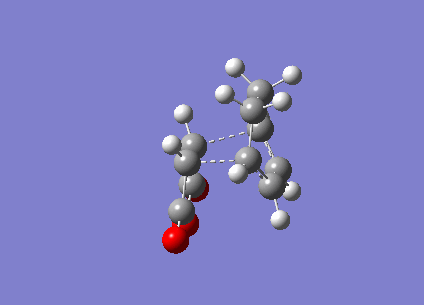
Figure 15 above is the vibration of the endo Transition State. The vibration the between the Carbons that would form the new bond is that of a bonding vibration of sufficient frequency (-802 cm^-1). The bond distances are identical and the vibration on both sides are near identical indicating that bond formation is synchronous.

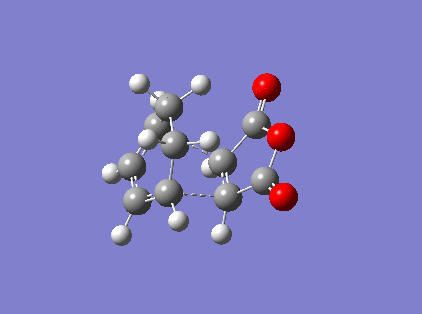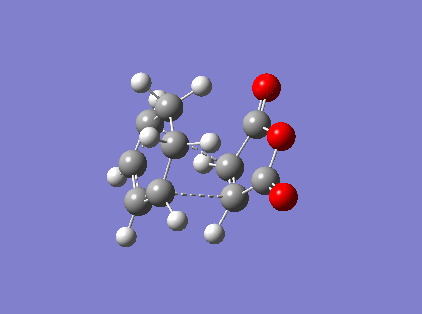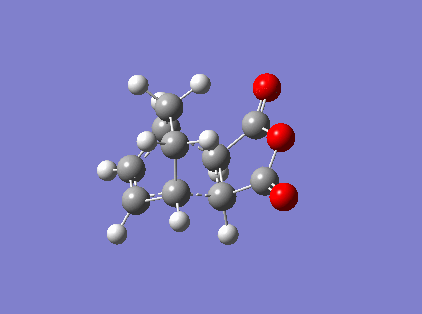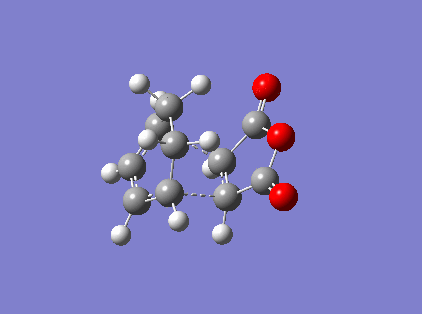
Figure 16 above is the endo vibration. The vibration the between the Carbons that would form the new bond is that of a bonding vibration of sufficient frequency (-818 cm^-1). The bond distances are identical and the vibration on both sides are near identical indicating that bond formation is synchronous.

Both products have a low positive frequency indicating that there is little driving force to form a bond in this structure. However, these structures must be close enough to the Transition State as indicated by the ability to perform some MO analysis of the HOMOs are both plausible.

Comment:

The energies of the exo and endo are slightly different. -0.06 au energy for TS. Endo and -0.05 au energy for TS. Exo. This indicates that the exo is higher energy. This is because of a couple of reasons. As shown by the sketch, the CH₂CH₂ bridge has the potential to have steric clashes with the maleic anhydride which is more likely to occur with the exo product since both groups are on the same face and likely to be Van der Waals repulsive./

Another factor is the secondary orbital effects: This information can be obtained by looking at the HOMO of the exo and endo product respectively./ The secondary orbital effect is a stabilization effect caused by the π bonds of the C=O on the maleic anhydride having favourable overlap with the C-C being formed in the transition state. This effect is more prominent in endo than in exo./

HOMO of exo and endo products

Figure 17: HOMO of Endo Obtained

Figure 18: HOMO of Exo Obtained

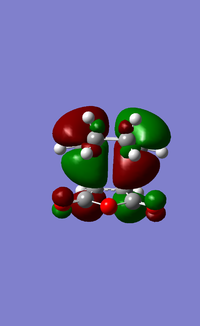
The HOMO is the endo shows that the side of orbital on the Oxygen nearest the newly forming C-C MO as shown by there green colour and brown parity part of the C=O π orbital with the brown orbital. In contrast, the LUMO has the opposite parity (brown) with the green parity and vice-versa. This small difference manifests itself into a secondary orbital effects, but the size of this effect cannot be determined with the information provided. More sophisticated methods are required to do this.

Neither of the structures were precisely at the transition state. This is due to the bond lengths of the carbon-carbon bonds in the cyclohexene ring are notthe same. The point group for the endo structure was C₁. An IRC calculation was attempted, but a result could not be obtained despite the lengthy calculation time. This would provide more information as to whether the structures optimized were the transition state or how far away these structures were form the true transition state. In my opinion, what has been produced by Gaussian are structures very close to the transition state and those structures could be altered and optimized to deliver the true transition state, but couldn't be done in this experiment due to time restrictions.

Summary

Conclusion

In conclusion, this experiment was mildly successful in studying the transition states of the Cope Rearrangments and Diels Alder. Physical data was obtained and the transition state was studied in detail. The Cope Rearrangement was a successful computation in obtaining the chair and boat transition states in relation to different conformers as well as the activation energy. The Diels Alder studies were less successful though it provides a basis for future study.

Further Experimentation

Because of the problems encountered throughout this investigation, further work would need to be done to get Transition States at HF and DFT as well as getting IRC for the endo and exo products. Due to the restricted time period this investigation was undertaken, this was a limited insight into the Transition States of Diels Alder reactions. Different Dienophile with different electron withdrawing groups could be investigated to see whether they would be endo or exo selective. The effect of Electron Withdrawing and Donating groups on the diene could also be investigated. The true transition states could be found so that the more detailed in depth analysis can be made using DFT. Calculations set to 0 K could be run to find the true values rather than using a correction factor.