Rep:Mod:jlphyswik
This is James Lees' physical component for 3rd year computational lab
Tutorial on the Cope Rearrangement
In this section I investigate the Cope rearrangement of 1,5-hexadiene as an example of how to study a chemical reactivity problem. The goals are to find the low energy minima and transition state structures using the potential energy surface of C6H10, a comparison of which should allow the determination of the preferred mechanism.To investigate the reaction the reactants/products were optimised allowing for the energy of the 1,5-hexadiene to be found and then contrasted with the energies from the optimised transition structures. This would allow for a determination of which transition structure is more likely to be involved, thus determining which pathway is kinetically favoured.
The reaction is a [3,3] sigmatropic shift rearrangement, a pericyclic reaction, which is thought to proceed through a boat or a chair transition state, this will be investigated at the B3LYP/6-31G level.
Optimising the Reactants and Products
First a molecule of 1,5-hexadiene was drawn in gaussview. This was then arranged such that the carbons were arranged to make the carbon carbon linkages in an anti conformation as shown. This was then optimised at the HF, 3-21G level.
 |
 |
This molecule belonged to the Ci point group and had an overall energy of -231.6925a.u. This meant that it was the same molecule as 'anti 2' from appendix 1.
Next a molecule of 1,5-hexadiene was drawn and arranged to give it gauche linkage. Again this was then optimised to the HF,3-21g level.
 |
 |
This molecule belonged to the C2 point group and had an overall energy of -231.6917a.u. This meant this molecule corresponded to 'gauche 4' from appendix 1.
The script indicated that the Ci conformer would be the lowest energy possible which had been my initial prediction when drawing that conformer. This is because this conformation both minimises steric interactions and allows favourable overlap of σ* C-H orbitals with adjacent σ C-H orbitals as shown in the diagram (note only 1 interaction is shown for clarity but more exist, these interactions are maximised in 'anti 2')
 |
The 'anti 2' conformer was then optimised using DFT, B3LYP 6-31g. A comparison between this structure and the HF 3-21g structure showed the bond lengths were all the same to 2d.p on the angstom scale, though some bonds were different in length at scales below this, these values are outside of the reasonable margin of error for bong lengths of ~.1A.
Next a frequency calculation was performed on the B3LYP 6-31g structure. This confirmed that the structure was a minimum by returning no negative frequencies for any vibrations. The IR spectrum of the compound is shown below along with the table of vibrations to confirm no negative frequencies were observed.

|
The following thermodynamic data was recorded:
This molecule is an asymmetric top.
Rotational symmetry number 1.
Rotational temperatures (Kelvin) 0.77951 0.06368 0.06269
Rotational constants (GHZ): 16.24234 1.32678 1.30635
Zero-point vibrational energy 376724.9 (Joules/Mol)
90.03941 (Kcal/Mol)
Optimising the Transition Structures
The chair and boat transition structures were now invesitgated using a variety of methods. I then performed an IRC calculation on each to demonstrate they truely were a transition state in the cope rearrangement. Finally, the relative energies of the transition states and the product were compared to allow for a determination of which reaction pathway is preferred, and this is is then discussed.
Computing Force Constants at the beginning
First an allyl fragment was drawn in gaussview and then optimised using HF, 3-31g. Two of these fragments were now arranged in a single mol group approximately 2.2A apart and in a shape that looked chair like. The chair transition state belongs to the C2h point group. An opt+freq calculation was performed on this molecule, optimising it to a TS(Berny) and at the 3-21g level. This returned a structure corresponding to the chair transition state. It was confirmed to be a transition state by analysis of the vibrational results which showed a single imaginary frequency at -818cm^-1. This vibration clearly corresponded to the cope rearrangement.
 |
 |
 |
 |
Using the Redundant Coordinator
Taking the initial guess at the transition structure from the 2 allyl fragments arranged into roughly a chair conformation, I now proceeded to find the transition structure using the redundant coordinate method. The first step was to freeze the 'bonds' between the 2 fragments. This was then minimised to a minimum. I then took this and changed the redundant coordinate editor options from freeze on the bonds to derivative. This was again minimised. The purpose of this sequence is that everything other than the interfragment geometry is optimised, then the interfragment geometry is minimised.
 |
The bond lengths between the fragments were 2.02A.
QST2 and QST3
In this section I investigated the QST2 and QST3 methods for finding transition structures.
First 2 molecules of 1,5-hexadiene were drawn such that they would be the 2 different forms following from the cope rearrangement. Care was taken to ensure the labelling of the carbons was consistant between the 2 molecules.
 |
These molecules were used as the inputs for a QST2 opt+freq calculation. This job failed with the returning proposed transition structure being of the following form:
 |
To correct this the 2 input molecules had their dihedral angles, and internal bond agles altered as in the script. The 2 input molecules now looked like:
 |
These were then used as the input for the QST2 calculation again. This time the calculation would not run. The returning error said 'Try using 3 structures as input for QST transition state search'. Therefore I decided to draw what I assumed the transition structure should look like and perform a QST3 calculation. Again care was taken to ensure consistant labelling between carbon atoms.
 |
This calcualtion was successfully completed, an imaginary vibration was observed at -839cm^-1 corresponding to the cope rearrangement via a boat transition state.
 | |
 |
 |
IRC
An IRC calculation was performed on the chair TS found from the first method, and on the boat TS found from the QST3 calculation. Both clearly showed that they were undergoing a cope rearrangement, but neither had reached a point which could be concluded to be a minimum, and certainly the Ci (anti2) molecule was not the end point for either calculation. Of the 3 options given at the end of the scripts section on IRC, I decided that computing the force constants at every step would be the best choice for finding which conformation they ended up in. This is because it should give the best result, and for a reasonably small molecule such as 1,5-hexadiene it shouldn't be massively time consuming. To save more time both jobs were submitted to SCAN.
| Stage | boat TS | chair TS |
|---|---|---|
| Beginning |  |

|
| End |  |

|
| Stage | boat TS | chair TS |
|---|---|---|
| Beginning |  |

|
| End |  |

|
It can be seen that after this kind of calculation the final geometry is much more easily observed. Whichever transition state pathway is followed, the optimal conformer for the end point is still anti2.
Activation Energies
The transition structures were now optimised to the DFT, B3LYP 6-31g level. A table showing comparisons between the transition structures and the product, hexadiene, is shown below.
| Property | Boat | Chair TS | 1,5-hexadiene |
|---|---|---|---|
| Energy/a.u. | -234.4928 | -234.5055 | -234.5597 |
| Fragment seperation/A | 2.25 | 2.03 | N/A |
| C-C bond length/A | 1.39 | 1.41 | 1.55 |
| C-C-C bond angle/degrees | 122.9 | 120.9 | N/A |
Making the activation energy for conversion through the boat transition state =0.0669a.u. or 165kJ.mol-1, or 41.98kCal.mol-1. The conversion through the chair transition state =0.0542a.u. or 142.30KJ.mol-1 or 34.01Kcal.mol-1. This matches fairly well to the literature values given in the script.
| Calculated chair pathway | literature chair pathway | calculated boat pathway | literature boat pathway |
|---|---|---|---|
| 34.01 | 33.5 | 41.98 | 44.7 |
The calculated value is closer for the chair form, though both are reasonably close, in fact the calculated value for the chair is within the margin of error for the literature value. Certainly the right order is observed between the 2 with the chair form requiring less energy than the boat form.
The Diels Alder Cycloaddition
In this section the Diels Alder reaction is studied as an example of comparing reaction pathways. The contribution of molecular orbitals to the reaction mechanism is looked at, and the reason for the high level of regioselectivity found in DA reactions is also investigated.
Reaction of Butadiene with ethene
 |
Cis-butadiene was constructed in gaussview and the MOs were found using the AM1 method.
| Cis-butadiene | HOMO | LUMO |
|---|---|---|
 |
 |

|
| It can be seen that the HOMO has 'a' symmetry with respect to the plane | The LUMO has 's' symmetry with respect to the plane |
For a pericyclic reaction the symmetry of the orbitals must be conserved. In the reaction the LUMO of butadiene is used, with electron density from the π bond of the ethene (the HOMO of ethene) donating into the butadiene's LUMO π*, breaking the double bonds in butadiene and forming 2 new sigma bonds. The π orbital of the ethene is obviously going to be symmetric with respect to the plane, and as such this reaction is allowed.
Next I looked to finding the transition state. The work on the tutorial section of the report had shown me that using the most simple method, calculating the force constants at the start of the reaction and minimising to a TS(Berny), provided the best accuracy to time results; at least for molecules as simple as are dealt with here. As such I drew what I believed should be the TS of the reaction.
 |
This was then put into an opt+freq calculation, minimising to a TS Berny at HF 3-21g level. This returned the following molecule for the transition state.
 |
This was the desired transition state structure, confirmed by the imaginary frequency found at -818cm^-1 which clearly corresponded to the DA reaction. The partly formed C-C sigma bonds were 2.21A. This is considerably longer than typical carbon-carbon bond lengths (sp3-sp3 1.54A, sp2-sp2 1.34A, vdw radius 1.7A)[1]. This might be expected as the transition structure is formed while the 2 molecules are some distance apart. The lowest positive frequency vibration corresponded to a twisting rotation of both the butadiene and the ethene, with each turning the oppposite direction.
 |
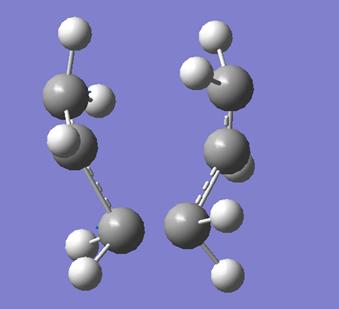 |
Both new sigma bonds form simultaneously, as is necessary for a pericyclic reaction which by definition involve a concerted motion of electrons. This can be seen in the above diagram where the view of the vibration on the right clearly shows the ethene and the butadiene coming together in a fashion that would cause both bonds to form at the same time.
The HOMO of the transition state structure is shown below
 |
It can be seen that the HOMO of this transition state structure is 's' symmetrical with respect to the plane used before. This mirror plane runs through the middle of the ethene double bond, then through the middle of the bond between the 2 central carbons in the butadiene part. The HOMO of the transition state is the MO involved in the reaction, and by being 's' symmetrical allows for the reaction to proceed, serving as further proof that this is the correct transition structure.
In conclusion of this section, for a pericyclic reaction, such as a Diels Alder reaction, to proceed, molecular orbital symmetry must be conserved. This is shown in this example by the HOMO of butadiene, the LUMO of ethen and the HOMO of the transition state all being 's' symmetric. The HOMO of the product of the reaction is also 's' symmetric.
 |
The regioselectivity of the Diels Alder reaction
In this section the regioselectivity of the Diels Alder reaction was investigated using the following reaction between maleic anhydrude and cyclohexa-1,3-diene as an example:
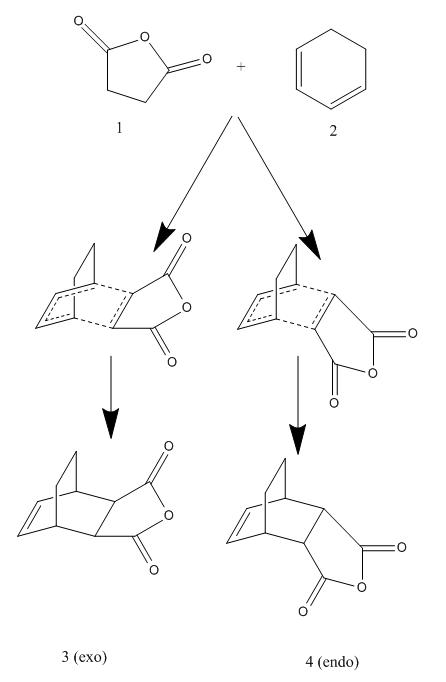 |
The reactants and products were first constructed in gaussview, then optimised to a HF 3-21g level.
 |
 |
 |
 |
The relative energies of 3 and 4 are shown below, note these can’t be compared with the reagents due to having a different number and type of atoms. The products, and eventually the transition states, can be compared though due to both having the same number (and type) of atoms. While trying to optimise the endo molecule (4) it kept minimising to the exo molecule(3) which was a further indication that the endo molecule is in a higher energy state. Eventually molecule 4 was constructed by taking the molecule of 3 and swapping the hydrogens with the furan ring rather than trying to draw it from scratch.
| Molecule 3 | Molecule 4 |
|---|---|
| -605.7187a.u. | -605.7213a.u. |
I first tried a Berny opt+freq calculation at the HF,3-21g level, using the following guess for the transition state of molecule 4:
 |
Which failed. Several imaginary frequencies were observed, none of which were even close to the reaction coordinate. Knowing the transition state should be effectively aromatic I put in the aromatic bonds and set up the calculation again using opt+freq minimising to a TS(Berny).
As it seemed unlikely I would be able to get the transition state molecule near the real thing by chance, I decided to take the product molecules and edit the bonding so that the furan ring and the other section were not bonded, a distance was set of 2A. A berny calculation was set up. This was taking a long time so I stopped it and sent it to SCAN.
This came back entirely successful. Below the transition state structure starting from product 4 is shown, followed by the imaginary frequency at -643cm-1 corresponding to the reaction coordinate.
 | |
 |
 |
The energy of this transition state was -605.6104a.u. Below are the HOMO and LUMO.
 |
 |
The HOMO is the molecular orbital of more interest for the same reasons as those mentioned in the first DA section. It can be seen that the HOMO is 'a' symmetric in the transition state of the endo molecule. Again this means that the molecular orbitals involved in the reaction must be of 'a' symmetry, which in this Diels Alder reaction corresponds to the HOMO of the maleic anhydride and the LUMO of cyclohexadiene(shown below).
 |
 |
 |
To find the transition state for molecule 3(exo) I effectively mirrored the furan ring, replacing the furan ring with the hydrogens and vice-versa. The returning molecule had an imaginary frequency at -533.9cm-1, this being the reaction coordinate. The overall energy was -605.7187a.u. and the imaginary vibrational frequency was at -533.9cm-1.
 | |
 |
 |
Below is a picture showing the 2 transition structures from the same orientation
 |
The partially formed carbon-carbon bonds in the transition state are of interest, specifically their bond lengths:
 |
The exo transition state has partly formed σ bonds of a longer length than in the endo transition state. This is a reason for the exo transition state being lower in energy. In both cases the partly formed σ bonds are longer than a usual length for fully formed σ bonds, and the closer to the normal length the partially formed bonds are the lower in energy they will be. One reason for this is that the orbital overlap between the ethene HOMO and the LUMO of the cyclohexa-1,3-diene will be poorer, resulting in a more diffuse orbital corresponding to the new σ bonds. More diffuse orbitals will result in a higher energy system, and in the endo transition state the orbitals in question are indeed more diffuse.
 |
The endo form is less strained than the exo form. This is because in the endo form the bridge only interferes with the hydrogens from the section that were on the furan, whereas in the exo form the entire furan ring is in this place causing a greater degree of unfavourable steric interactions.
The endo transition state is also favoured over the exo transition state due to secondary orbital overlap. In the endo transition state the carbonyl groups on the maleic anhydride are also able to contribute favourably to the partially formed σ bonds, thus stabilising them, which is why the partially formed bonds are shorter in the endo form, and another reason for the endo transition state being lower in energy, which in turn causes the preference for the endo product over the exo product. This can be shown in the image[2] below.

|
A table comparing properties of molecules and their transition states:
| Molecule 3 | 3 TS | Molecule 4 | 4 TS | |
|---|---|---|---|---|
| Energy/a.u. | -605.7187 | -605.9421 | -605.7213 | -605.6104 |
| Imaginary frequency/ cm^-1 | N/A | -533.9 | N/A | -643 |
| HOMO |  |
 |
 |

|
| LUMO |  |
 |
 |

|
The difference in energy between the 2 products is only 1.6Kcal.mol-1. Such a small difference means that the reason for the preference of the endo form cannot be thermodynamic. The difference in energies between the product and transition state however through the 2 pathways is more notable. 140.1856kCal/mol for 3 and 69.59082kCal/mol for 4. Clearly then the endo form is preferred for kinetic reasons.
The imaginary vibration is at a lower frequency for the endo transition state. This would indicate that the reaction pathway from the transition state to the product requires less energy, again showing this pathway is energetically favoured.
References
- ↑ Organic Chemistry, M.A. Fox, J.K. Whitesell, 2004, pg49, ISBN:0763721972
- ↑ http://commons.wikimedia.org/wiki/File:Cyclopentadiene_Maleic_Anhydride_Diels_Alder.png