Rep:Mod:jlm2014

Computational chemistry : Module 3

The Cope rearrangement tutorial

Optimizing the reactants and products

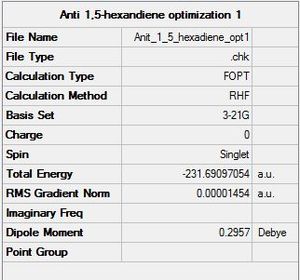
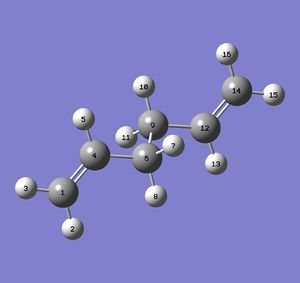
A) The summary of the optimization is shown below:

Summary of the optimization (anti)

Summary of the optimization (anti)

!!

The energy calculated by Gaussian is -231.69097054 Hartree. An isolated value is not relevant, it can not be interpreted but only compared with the energy of similar molecules.

The point group found by Gaussian is C₁. The same result has also been found "manually" with the help of a point group flowchart. This is a coherent result given the poor symmetry of the molecule.

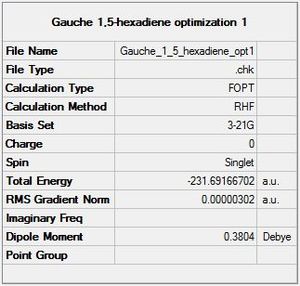
B) The summary of the optimization is shown below:

Summary of the optimization (gauche)

Summary of the optimization (gauche)

!!

The gauche conformer will probably be less stable than the anti conformer because the gauche conformer is sterically more hindered than the anti conformer. One could imagine that the gauche conformer could be stabilized by conjugation but the orientation of the two π systems is not optimal.

The energy calculated by Gaussian is -231.69166702 Hartree. Consequently, according to the Gaussian calculation, the gauche conformer is 1.83 [kJ/mol] more stable than the anticonformer. This result contradicts the above hypothesis. Nevertheless, the energy difference is relatively small and it is difficult to have the same accuracy without doing calculation.

The point group found by Gaussian is C₁. The point group found "manually" is also C₁. This is coherent with the low symmetry of the molecule.

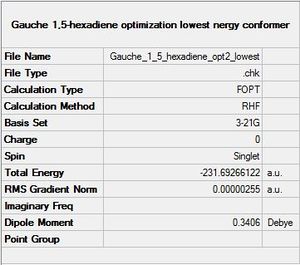
C)The lowest energy conformer will be the less hindered. The best way to avoid constrains is to minimize the H-H interactions and to optimize the C-C angles. Consequently, the conformation of C₃ and C₄ should be "staggered" and the hydrogen atoms on C₂ and C₅ should not interact with the hydrogen atoms on C₃ and C₄. Such a molecule has been drawn in Gaussview, the summary of the optimization is shown below.

Summary of the optimization (lowest energy conformer)

Summary of the optimization (lowest energy conformer)

!!

The energy of this conformer is -231.69266122 Hartree, it is then 2.61 [kJ/mol] more stable than the previous "gauche" conformer and 1.06 [kJ/mol] more stable than the "anti" isomer.

D) The above "anti" conformer corresponds to the "anti 4" conformer in the "Appendix 1". The above "gauche" conformer corresponds to the "gauche 2" conformer in the "Appendix 1". FInally, the lowest energy conformer corresponds to the "gauche 3" conformer in the "Appendix 1".

The comparison of all those molecules is only based on the comparison of the energy. Anyway, in the three cases, the structure of the molecules is similar.

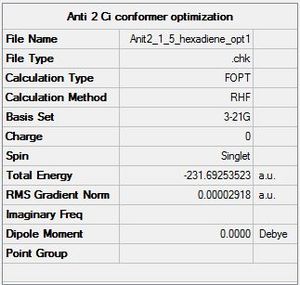
E) The "anti 2" conformer has been created in Gaussview. The summary of the calculation is shown below:

Summary of the optimization (Anti 2)

Summary of the optimization (Anti 2 conformer)

!!

The calculated energy and the "appendix 1" energy are the same. The point group found by Gaussview is C_i.

F) The general shape of the molecules does not change with the DFT B3YLP 6- 31G(d) but some geometrical values are slightly different. The following table list this differences.Because of the C_i symmetry of the molecule the angles of only half of the molecule have been listed.

Atom labels

Atom labels

!!

Differences between HF 3-21G and DFT B3LYP/6-31G(d):

Measure	HF 3-21G	DFT B3LYP/6-31G(d)
(3,1,2) angle	116.3°	116.5°
(1,4,5) angle	119.7°	118.9°
(5,4,6) angle	115.5°	115.8°
(7,6,8) angle	107.7°	106.8°
(4,6,9) angle	111.4°	112.4°

The bong lengths are also different but in all the cases, the difference was smaller than 0.01 [Å] which is the accuracy limit of Gaussview.

G) The different values of energy calculated by Gaussian are listed below:

Sum of electronic and zero-point Energies= -232.830852 [Hartree] Sum of electronic and thermal Energies= -232.823847 [Hartree] Sum of electronic and thermal Enthalpies= -232.822903 [Hartree] Sum of electronic and thermal Free Energies= -232.862124 [Hartree]

Optimizing the "Boat" and "Chair" transition structures

B) The calculation gave the expected imaginary frequency of 818[cm^-1]. The corresponding vibration is shown below.

Imaginary vibration

Chair TS calculated with the first method

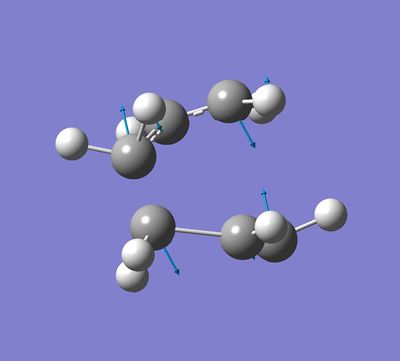This vibration correspond to the Cope rearrangement mechanism. One can see that this vibration closer the two terminal carbon atoms.

D) The following table shows the chair transition state optimized with the tow methods. The differences between the angle values and the bond lengths are also presented.

Measure	First method	Second method
	Chair TS calculated with the first method	Chair TS calculated with the second method
Distance between two terminal allyl C	222 [pm]	220 [pm]
C-C bond length (in the same allyl)	139 [pm]	138 [pm]
C-C-C angle	124.3°	122°
H-C-H (terminal angle)	117.5°	115°

G) The following table shows the calculated energies for the two TS and for the reactant:

	Reactant	Chair TS	Boat TS
Electronic energy (HF/3-21G)	-231.692535 [a.u]	-231.616309 [a.u]	-231.602801 [a.u]
Electronic + zero point energy (HF/3-21G)	-231.539539 [a.u]	-231.465353 [a.u]	-231.450918 [a.u]
Electronic + thermal energy (HF/3-21G)	-231.532565 [a.u]	-231.460244 [a.u]	-231.445283 [a.u]
Electronic energy (B3LYP/6-31G*)	-234.610240 [a.u]	-234.554485 [a.u]	-234.540434 [a.u]
Electronic + zero point energy (B3LYP/6-31G*)	-234.467365 [a.u]	-234.411639 [a.u]	-234.398474 [a.u]
Electronic + thermal energy (B3LYP/6-31G*)	-234.461867 [a.u]	-234.405179 [a.u]	-234.392540 [a.u]
Activation energy (0[K], HF/3-21G)	-	46.55 [kcal/mol]	55.61 [kcal/mol]
Activation energy (298.15[K], HF/3-21G)	-	45.38 [kcal/mol]	54.77 [kcal/mol]
Activation energy (0[K], B3LYP/6-31G*)	-	39.02 [kcal/mol]	43.80 [kcal/mol]
Activation energy (298.15 [k], , B3LYP/6-31G*)	-	35.57 [kcal/mol]	43.50 [kcal/mol]
Experimental values (0[K})	-	33.5 +/- 0.5 [kcal/mol]	44.7 +/- 2 [kcal/mol]

The calculated activation energies of the chair TS are, with the two methods, closer to the experimental values than the activation energies of the boat TS. Consequently, one can deduct that the real reaction path implies a chair TS.

The Diels Alder reaction

1) The following table shows the HOMO and the LUMO of the cis-butadiene and of the ethylene. For the cis-butadiene, the HOMO is antisymmetric with respect to the plan between C2 and C3 and the LUMO is symmetric with respect to the same plan. For the ethylene, the HOMO is symmetric and the LUMO is antisymmetric.

HOMO	LUMO
HOMO of the cis butadiene	LUMO of the cis-butadiene
HOMO of the ethylene	LUMO of the ethylene

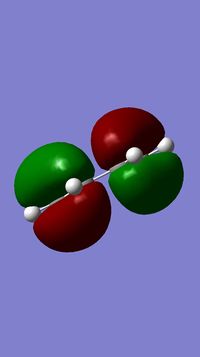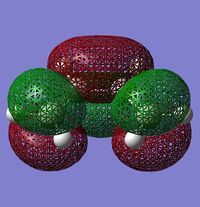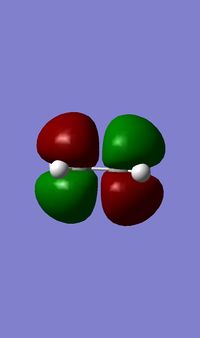2) The transition state of the Diels Alder reaction has been calculated in two steps. The first steps was a QST2 calculation usine the semi empirical AM1 method. This calculation failed (). Anyway, the "failed" calculated TS did not seem far from the expected TS (same geometry and only one negative frequency which corresponds to the expected mechanism). Consequently, this "failed" TS has been optimized to a transition state using the semi empirical AM1 method. The following table shows different data about this transition state.

TS of the Diels-Alder reaction

Vibration	Freqency	Electronic energy of the TS	Electronic energy of the Reactants	Activation energy	Literature value (activation energy)
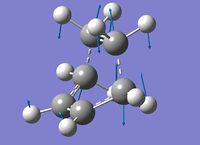Negative vibration of the TS	-956.2 [cm-1]	0.111655 [a.u]	0.073991 [a.u]	23.6 [kcal/mol]	25.2 +/- 0.1 [kcal/mol]

The following table shows the HOMO and the LUMO of the calculated TS:

HOMO and LUMO of the TS

HOMO	LUMO
HOMO	LUMO

One can clearly see that the HOMO of the TS (antisymmetric) is an interaction between the butadiene HOMO and the ethylene LUMO (the both are antisymmetric).

The length of the new σ bond of the TS is 212 [pm], which is shorter than the bond length calculated in this article (221.7 [pm]), but much more longer than a typical C_sp³-C_sp³ bond (154 [pm]), or C_sp²-C_sp² bond (147 [pm]). This difference can be explained by the fact that the new σ bond is only partially formed, the orbital overlap is not complete.

Finally, a IRC calculation has been carried out. The following movie shows the complete mechanism of the reaction (you must click on the picture to see the animation).

Diels Alder reaction. Complete mechanism

Mechanism of the Diels-Alder reaction

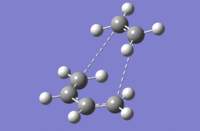This animation clearly shows how the vibration of the butadiene allows the overlap of the frontier orbitals and consquently the formation of the new σ bonds. Furthermore, on can see the how the two double bonds of the butadiene disappear (and form the new σ bonds) and how the double bond of the cyclohexene appears.