Rep:Mod:jlm2013

Computational chemistry lab : module 2

Questions in the part "using pseudo-potentials":

1) What is the optimised Tl-Br bond distance? The optimised Tl-Br bond is 2.69 [Å]

2) What is the optimised Br-Tl-Br bond angle?

The optimised Br-Tl.Br bond is 120°

Optimisation of TlBr3: summary

File name	TlBr3_optimisation
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-91.21812851 [a.u.]
RMS Gradient Norm	0.00000090 [a.u.]
Imaginary Freq
Dipole Moment	0.0000 [Debye]
Point Group	D3H
Job cpu time: 0 days 0 hours 0 minutes 27.0 seconds.

Link to the optimized file: Optimization file: DOI:10042/to-9980

Questions is the part "animating the vibrations":

Link to the population analysis : DOI:10042/to-9982 The charge numbers of the H atoms are : -0.111. The charge number of the B atom is : 0.332.

Vibrations analysis:

The following table summarizes the six different vibrations of the molecule:

Vibrations of BH3

N°	Form	Frequency	Intensity	Symmetry
1	1st vibration	1146.03	92.66	A2" (inversion with 3C2, σh and 2S3)
2	2nd vibration	1204.86	12.39	E'
3	3rd vibration	1204.86	12.39	E'
4	4th vibration	2591.65	0.0	A1'
5	5th vibration	2730.07	103.86	E'
6	6th vibration	2730.07	103.85	E'

The IR spectrum of the molecule is the following:

IR spectrum of BH3. In increasing order : vibration 1, 3 and 6.

IR spectrum of BH3

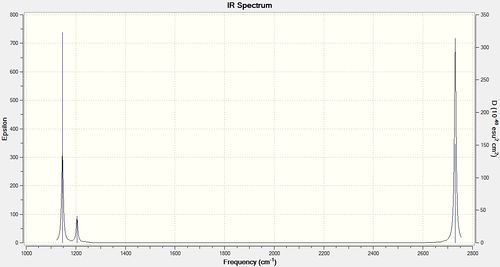The reason for which only the vibrations 1, 3 and 6 are visible on the IR spectrum is that they are the only ones that change the dipole moment of the molecule. The dipole moment is changed if the vibrations are not symmetrical about the plan σ_n and/or σ_h.

Optimisation of TlBr3:

1) What is the calculation method?

The calculation method used in this optimization is the DFT B3YLP. The DFT B3YLP method is used because it doesn't require a lot of computational work and and produces results that are accurate enough to analyse TlBr3.

2) What is the basis set?

The basis set of equations is Lan2DZ. The thallium and the bromide are relatively big atoms (especially the thallium). In order to simplify the calculation, the core electrons (that don't have a role in the bonding according to valence bond theory) will be "replaced" by a core potential function (imitating the core electrons). That's the role of the Lan2DZ set.

3)Why must you use the same method and basis set for both calculations?

The frequencies analysis is carry out to determine is the optimized structure is really a minimum. If the frequencies analysis is conducted on a molecule different from the optimized one (e.g. the methods or sets are different), then it will be impossible to deduct anything about the energy of the optimized molecule (is it a minimum? a transition state ?).

4) Why do you have to carry out a frequencies analysis?

To be sure that the energy of the optimized molecule is really a minimum, the energy function of the molecule must be studied. Mathematically, if the gradient of a function is equal to zero in a point (x,y,z) it's possible to say that this point is an extremum, but impossible to say if it's a minimum or a maximum. The analysis of the laplacian of the function will determine if the point (x,y,z) is actually a minimum or a maximum. The frequencies analysis is calculated with the second derivative of the potential energy surface of the molecule. Consequently, study the vibrations give information on the energy.

5) What are the low frequencies of TlBr3 ? What is the lowest real normal mode?

The low frequencies of TlBr3 are the following:

Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449

The lowest real normal mode is 0.0015 [cm^-1].

6) Compare the optimised Th-Br bond distance to others you find in the literature.

This article . about "Structure of Thallium(III) Chloride, Bromide, and Cyanide Complexes in Aqueous Solution" provides experimental measurements and other literature data. The article reports a bond length of 2.52 [Å] and the literature quoted (in the article) a bond length of 2.51 [Å]. The distance found in the optimised module is 2.65 [Å]. The relative difference is ~5%. This can be explained probably by the fact that the article measurements concern complexes in water while Gaussian calculates data for a isolated molecule.

7) In some structures Gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?

The fact that Gaussview doesn't draw the bonds doesn't mean they are not there. Gaussview doesn't draw the bonds when they are not in the range of the "allowed" values (to short or to long).

8) What is a bond?

A chemical bond is created by a constructive interference between two atomic orbitals. The constructive interference means that the probability of finding the electrons between the two nuclei is big. The constructive interference is lower in energy than the destructive interference, so it will be populated first (according to the "aufbau" principle). The bond length will vary over time because it's an equilibrium situation including electrostatic forces (nuclei-electron attraction, electron-electron and nuclei nuclei repulsion).

MO diagram of BH3

Optimized file: DOI:10042/to-9979

The MO diagram of BH3 is the following:

MO diagram of BH3

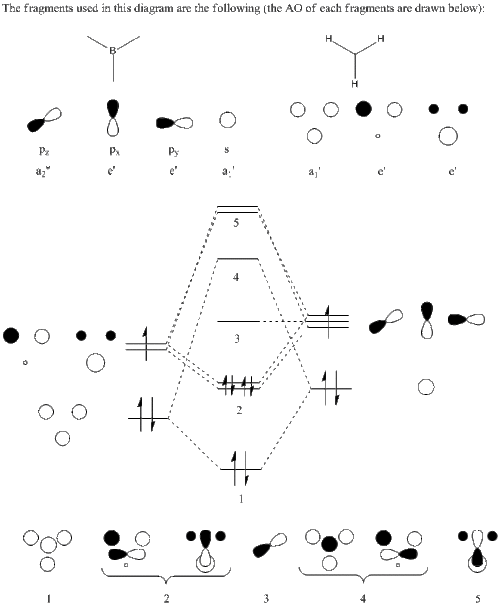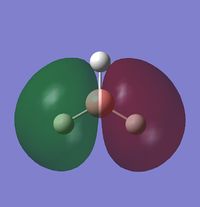
The occupied orbitals are the MO 1 and 2 while the LUMO is the MO 3.

The real MOs are shown below:

MO 1

MO 2a

MO 2b

MO 3

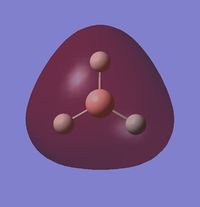1) Are there any significant differences between the real and LCAO MOs?

There are not really significant differences between the LCAO and the MOs. The only difference is that the MOs are more realistic than the LCAO (they are not only schematic) but, qualitatively, they are the same (shape, phase, position).

2) What does this say about the accuracy and usefulness of qualitative MO theory?

The absence of significant differences between the LCAOs and the MOs shows that the MO theory is relevant and can be used to describe molecules and predict their reactivity or properties. However, as seen in the "module 1", in the case of more complicated molecules, the MO diagram becomes really difficult to draw and it's more complicated to compare LCAOs and MOs (here LCAOs and MO match very well because BH3 is a small and simple molecule).

Isomers of Mo(CO)₄L₂

Structures

Optimized files:

Cis isomer: DOI:10042/to-9974 Trans isomer: DOI:10042/to-9975

Trans complex

The trans isomers has a high symmetry level. Therefor, it is expected that this complex will have a tidy geometry. In fact, that exactly what it is observed. All the ligand - metal - ligand angle are right (small deviation listed below), and the two PCl₃ groups are totally eclipsed (they have been oriented in this conformation manually but one can see that the dihedral angle has not changed during the second and the third step of the optimization).

The following table lists all the important geometrical information of the complexe and information found in the literature (PCl₃ and POCl₃) (trans-Cr(CO)₄(PPh₃)₂

It is important to know that because of the ligand and conformation differences between the cis-[Mo(CO₄)(PCl₃)₂] and the cis-[Mo(CO₄)(PPh₃)₂] it has not been possible to compare directly the angles and the bond lengths. The values marked with a "*" values ​​are either average or values ​​without direct correspondence between the two complexes. There are represented here to compare the calculated values and the experimental data measured on a similar complex.

Trans molybdenum complex

Measure	Complex	PCl3	POCl3	trans-Cr(CO)4(PPh3)2	Atom numbers
P-Mo bond	242 [pm]	-	145 [pm]	236* [pm]
Cl-P bond	211 [pm]	204 [pm]	199 [pm]
C-Mo bond	205 [pm]	-	-	187* [pm]
O=C bond	117 [pm]	-	-	115 [pm]
Cl-P-Cl angle (16,11,17) & (12,10,14)	99.8°	100°	103°	-
Cl-P-Cl angle (all the other angles)	100.2°	100°	103°	-
Cl-P-Mo angle (15,11,1) & (13,10,1)	119.6°	-	115°	-
Cl-P-Mo angle (all the other angles)	116.8°	-	115°	-
C-Mo-C angle (3,1,5) & (3,1,2)	90.8°	-	-	92.2°* (3,1,5), 84°* (3,1,2)
C-Mo-C angle (2,1,4) & (5,1,4)	89.2°	-	-	92°*

One can see that the P-Mo bond is longer than the P=O bond; obviously this is because Mo is bigger than O. The Cl-P bonds are longer in the complex than in the reference molecules. This can be explained by a π-backbonding that fills the π* orbitals of the Cl-P bonds and, consequently, weakens them. This phenomenon is also observed in the C=O bond which is longer in the two complexes than the in isolated C=O (112 [pm]). The main difference between the references and the complex is the fact that, in the complex, the PCl₃ groups is deformed and has lost its symmetry. The Cl-P bond that is different from the two others is the one that is parallel to one C-Mo bond. This mean that the explanation of this difference is probably linked to a repelling interaction between the C-Mo bond and the Cl-P bond. A MO analysis of the complex could clearly show this phenomenon. The Cr complex chosen as reference has shorter bond lengths because Cr is a smaller atom than Mo. The angles presented in the Cr complex can not be compared to those presented in the Mo complex because the conformation of the PL₃ groups is different (eclipsed in the Mo complex, staggered in the Cr complex).

Cis complex

The following table lists all the important geometrical information of the complexe and some data found in the literature (PCl₃ and POCl₃) , cis-[Mo(CO₄)(PPh₃)₂]. It is important to know that because of the ligand and conformation differences between the cis-[Mo(CO₄)(PCl₃)₂] and the cis-[Mo(CO₄)(PPh₃)₂] it has not been possible to compare directly the angles and the bond lengths. The values marked with a "*" values ​​are either average or values ​​without direct correspondence between the two complexes. There are represented here to compare the calculated values and the experimental data measured on a similar complex.

Cis molybdenum complex

Measure	Complex	PCl3	POCl3	cis-[Mo(CO4)(PPh3)2]	Atom numbers
P-Mo bond	247 [pm]	-	145 [pm]	257 [pm]
Cl-P bond	211 [pm]	204 [pm]	199 [pm]	183* [pm]
C-Mo bond (1,2) & (1,5)	202 [pm]	-	-	197 [pm]
C-Mo bond (1,3) & (1,4)	205 [pm]	-	-	204* [pm]
O=C bond	117 [pm]	-	-	115* [pm]
Cl-P-Cl angle (14,10,12) & (16,11,15)	100.7°	100°	103°	104°*
Cl-P-Cl angle (12,10,13) & (16,11,17)	100.2°	100°	103°	102°*
Cl-P-Cl angle (13,10,14) & (17,11,15)	99.6°	100°	103°	99°*
Cl-P-Mo angle (12,10,1) & (16,11,1)	119.5°	-	115°	124°*
Cl-P-Mo angle (13,10,1) & (17,11,1)	115.9°	-	115°	116°*
Cl-P-Mo angle (14,10,1) & (15,11,1)	117.6°	-	115°	109°*
C-Mo-P angle (3,1,11)	92.2°	-	-	84.4
P-Mo-C angle (10,1,3)	88.7°	-	-	90.3°
Cl-P-Mo-C dihedral angle (12,10,1,4)	6.9°	-	-	-
Cl-P-Mo-C dihedral angle (16,11,1,3)	6.9°	-	-	-

Comparison Cis-Trans

The bond lengths are the same in the two complexes. The main differences are observed in the values of the angles. It's interesting to see that in the two complexes the PCl₃ ligands have lost their original symmetry but that in the trans complex the PCl₃ ligands have still a planar symmetry (plan passing by the Mo atom, two C atoms and two Cl atoms). The same ligands have totaly lost their symmetry in the cis complex (the three angles and bonds have a different value) because of the repulsive interaction between them. This repulsion is visible in the P-Mo-P angle which is 94.3° and in the fact that the P, Mo and C atoms are not aligned. The trans complex has also a deformation due to a repulsion of the PCl₃ groups. This repulsion bends the complex in direction of the z axis (perpendicular to the plan that contains two P , 2 C , the Mo and no Cl) and is probably due to the P-Cl/C-Mo bonds interaction mentioned above.

Relative energy

The summaries of the two calculations are shown below:

Summaries

	Trans complex	Cis complex
Calculation type	FREQ	FREQ
Calculation method	RB3LYP	RB3LYP
Basis set	Gen	Gen
Charge	0	0
Spin	Singlet	Singlet
E(RB3LYP)	-623.69415611 [a.u.]	-623.69291202 [a.u.]
RMS Gradient Norm	0.00000174 [a.u.]	0.00005404 [a.u.]
Imaginary Freq	0	0
Dipole Moment	0.2292	0.0694 [Debye]
Point Group	C2V	C1

The energy difference between the two isomers is 1.24408 10^-3 [a.u] = 5.42387 10^-24 [J] = 3.26633 [kJ/mol]. This result is presented here with an excessive accuracy. Effectively, it's smaller than the error range of Gaussian (which is +/- 10[kJ/mol]. Anyway, this result can interpreted; it means that the two isomers have the same stability.

It is reported in this article that, with the metals of the group VI, the cis conformation is favored when the complex has small ligands but that the trans conformation becomes more stable as the size of the ligands increases. In the same article the energies of cis and trans [Mo(CO₄)(PPh₃)₂] have been calculated and the results shows a clear preference for the cis isomer (ΔE = -72.98 [kJ/mol]). Then, the fact that the energy difference calculated between the cis and trans PCl₃ complexes is small can not be explained by the fact that the PCl₃ ligands are smaller than the PPh₃.

In an other article , it is shown that, in the same kind of group VI metal complexes, a attractive interaction between the ligands can favor the cis isomer. The authors go further and show that the interaction between the ligands is more important than the size of the ligands (in terms of isomerism).

The two articles mentioned above demonstrate that the electronic effects are more important than the steric effects in the stabilisation of a complex. Then, the absence of stability difference between the two complexes studied here shows that there are no electronic interaction between the two PCl₃ ligands. A repulsion exists in the cis complex but it is minimized by the fact that the two PCl₃ are inverted (one is pointing up and the other is pointing down). This repulsion could explain the small preference for the trans isomer.

This considerations suggest that it is possible to favor one isomer over the other simply by selecting the good ligands. Ligands that can attract each other (benzene ring with π-stacking, anion-cation, H-bonds,...) will product a cis isomer, ligands that repels each other (anion-anio, cation-cation, lone pairs, size) will product a trans isomer.

IR spetra

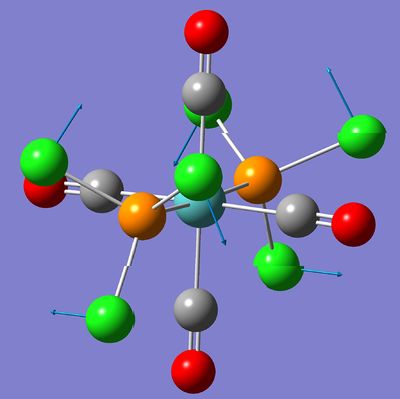
The following pictures show the lowest frequency vibration of the two isomers. This vibration is a "rotation" of the PCl₃ groups around the P-Mo bond.

Low frequency vibrations

Trans complex	Cis complex
Lowest frequency vibration of the trans complex	Lowest frequency vibration of the ciscomplex

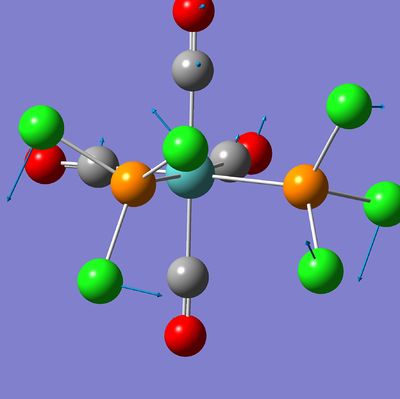At room temperature, this vibration will have more energy and then it is possible that the PCl₃ undergo a complete rotation around the P-Mo bond.

The IR frequencies of the carbonyl are listed below:

IR frequencies of the carbonyl

Trans	Symmetry	Cis	Symemtry	Literature
1939 [cm-1]	A1	1938 [cm-1]	A
1939 [cm-1]	B2	1941 [cm-1]	A
1966 [cm-1]	A1	1952 [cm-1]	A
2025 [cm-1]	A1	2019 [cm-1]	A

The trans complex has a C_2v symmetry. According to the C_2v character table, all the vibrations with a A2 symmetry will not be visible on the IR spectrum. In fact, that is what is observed on the IR spectrum generated by Gaussview. The cis complex has a C1 symmetry. According to the C₁ character table, all the vibrations will be visible on the IR spectrum. In fact, that is what is observed on them IR spectrum generated by Gaussview. In the two complexes some vibrations have very low intensity but it doesn't mean that they don't exist.

Mini project : Bonding in Al₂Br₂Cl₄ isomers

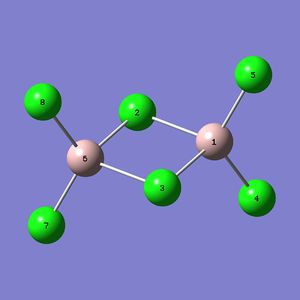
The Al₂Br₂Cl₄ molecule can have different isomers (shown below). The aim of this project is to use Gaussian to optimize this isomers, calculate their vibrational frequencies and use the produced data to study the influence of the two Br atoms position.

Since the molecules are small (only 8 atoms the optimization can be made with an accurate method. The optimization has been carried out in 3 steps. The first step was a manual optimization using the date provided by this article . The second step was an optimization with the MP2 6-G31 (d,p) method. Eventually, the last step was an optimization with the MP2 6-G311 (d,p) method. The efficiency of the optimization has then been checked with a frequency analysis. All the calculated frequencies where positive and the low frequencies where within [-2;1] [cm^-1]. One can then deduct that the optimization has produced good results.

The following table shows the studied molecules :

Al₂Cl₆ and Al₂Br₂Cl₄ isomers:

Molecule	Summary	Optimization file
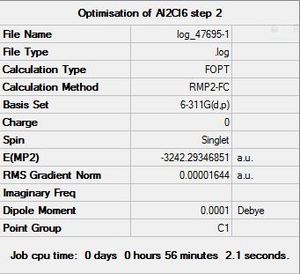Al2Cl6	Al2Cl6 calculation summary	DOI:10042/to-9936
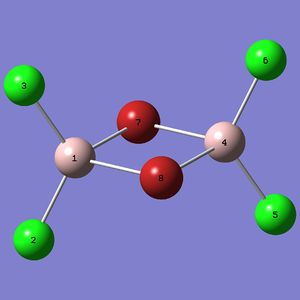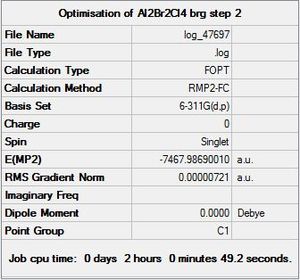Al2Br2Cl4 with bridging bromide atoms	Al2Br2Cl4 with bridging bromide atoms calculation summary	DOI:10042/to-9934
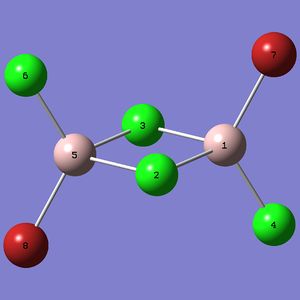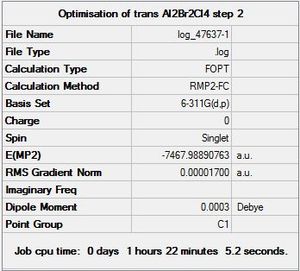Al2Br2Cl4 with trans bromide atoms	Al2Br2Cl4 with trans bromide atoms calculation summary	DOI:10042/to-9721
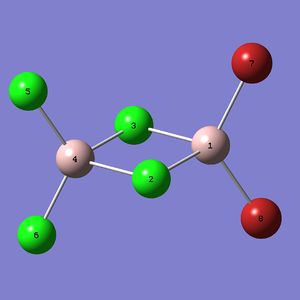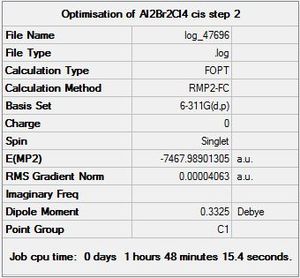Al2Br2Cl4 with cis bromide atoms	Al2Br2Cl4 with cis bromide atoms calculation summary	DOI:10042/to-9935

Energy

The cis and the trans isomer have the same energy, one can not say which one is the more stable. The compound with bridging bromide atoms is 5.23 [kJ/mol] less stable than the cis and the trans isomer. This result can not be interpreted since the error range of Gaussians is +/- 10 [kJ/mol].

The fact that the energies of the different isomers are almost equivalent means that the molecule is not sensible to atom change. The only difference between chloride and bromide is the size (bromide is bigger than chloride). A molecule with a geometry comparable to Al₂Cl₆ is not very hindered. Consequently, substitute a small atom by a bigger atom will only increase the bond lengths but will not modify the angles of the molecule or create new steric constrains. That is the reason why there is no really more stable isomer than an other.

Structure

The following table shows all the important geometric parameters of the molecules:

Measure	Al2Cl6	bridging Al2Br2Cl4	trans Al2Br2Cl4	cis Al2Br2Cl4	Literature (Al2Cl6)
Terminal angle	122.4°	121.3°	122.4°	122.6° (Br-Al-Br); 122.3° (Cl-Br-Cl)	121.76°
Ring angle (Al-X-Al)	88.9°	86.2°	89.0°	89.0°	89.32°
Terminal bond length	207 [pm]	207 [pm]	207 [pm] (Al-Cl); 223 [pm] (Al-Br)	207 [pm] (Al-Cl); 223 [pm] (Al-Br)	207.7 [pm]
Ring bond length	226 [pm]	243 [pm]	226 [pm]	226 [pm]	227.8 [pm]

The calculated data are compatible with what has been found in the literature. This relative equivalence between the two different measurement (calculated vs literature) is probably caused by the fact that the isomers have been manually optimized with the same literature reference. However, it is reasonable to think that similar results would also have been found without the manual optimization since the MP2 6-G311 (d,p) method is accurate.

It is interesting to observe the relative stability of the parameters. This is compatible with the observations made on the energies. The only noticeable change in the measures occurs with the bridging isomer. One can see that the ring angle decreases as the ring bond length increases. This is obviously caused by the fact that the bromide atoms are bigger than chloride atoms. That can also explain the small energy difference found between the cis/trans and bridging isomer.

An other interesting point is that the point groups calculated by Gaussian are false (C1 instead of D2h for Al₂Cl₆ and the bridging isomer, C1 instead of Cs for the trans and the cis isomer). No explanations have been found to explain this error.

Molecular orbitals and vibrational frequencies

Because of the power outage that happened Monday morning I do not have the time to completely develop this part of the project. Nevertheless I briefly mention some other interesting points.

Concerning the MOs, the population analysis shows that there is an overlap of the p orbitals of the X (Br and Cl) atoms in the ring. Qualitatively, this means that there should be a bond between those two halogens (this overlap is more important with Br because of its size). There is also an important conjugation of the p orbitals of the halogens (terminal and bridging), this must stabilize the molecule (this ring can probably be compared to cyclobutadiene ). This conjugation is probably more important with Br than with Cl, consequently, Al2Br6 must be more stable than Al2Cl6.

Concerning the vibrations, the lowest one is a bending of the ring along the bridging X-X axis. The frequency of this vibration is lower with Br than with Cl. This fact can be explained by a better conjugation with Br and consequently a more rigid ring

REFERENCES: