Rep:Mod:jlm2012

Computational chemistry

Module 1: Part 1: Dimerisation of the cyclopentadiene

The cyclopentadiene can undergo a Diels-Alder addition with itself. The resulting product has two different isomers : the exo isomer and the endo isomer.

We will give an explanation of the stability difference of the two isomers using "ChemBio3D ultra". The explanation will be based on the calculation made by the software (ChemBio3D ultra uses allinger MM2 molecular mechanics models).

The results are the following:

Energy type	Exo product in [kcal/mol]	Endo product in [kcal/mol]
Stretch	1.28	1.25
Bend	20.58	20.85
Stretch-Bend	-0.84	-0.84
Torsion	7.66	9.51
Non-1,4 VDW	-1.42	-1.54
1,4 VDW	4.23	4.32
Dipole/Dipole	0.378	0.45
Total Energy	31.88	34.0

The calculation shows that the biggest energy difference between the two isomers comes from the torsion. Obviously, the endo isomer is more twisted than the exo isomer. We tried to compare the dihedral angles of the two isomers but I has not been possible to determine if the difference comes only from the endo/exo ring or from an other part of the molecule. Anyway, one can say that the endo product is thermodynamically less stable than the exo product. Since the endo product is the major product of the dimerisation, one can deduct that this reaction is kinetically controlled.

The two isomers

Exo isomer	Endo isomer
Exo dimer	Endo dimer

Hydrogenation of the isomers:

The endo or the exo isomers can be hydrogenated. The hydrogenation can take place on the six member ring or on the five member ring. ChewBio3D can help to determine which position will be preferred in the hydrogenation process.

The results are the following:

Energy type	Add. on the 6-membered ring (prod 4) in [kcal/mol]	Add. on the 5-membered ring (prod 3) in [kcal/mol]
Stretch	1.10	1.28
Bend	14.52	19.86
Stretch-Bend	-0.55	-0.83
Torsion	12.50	10.81
Non-1,4 VDW	-1.07	-1.22
1,4 VDW	4.51	5.63
Dipole/Dipole	0.14	0.16
Total Energy	31.1520	35.6850

The product 3 is thermodynamically less stable than the product 4. The explanation is that in the product 3, the double bond creates more steric constrains than the double bond in the product 4. The biggest difference comes from the bending energy. This is because the angles between the double bond and the simple bonds in the molecule 3 are really smaller than the optimal value (107° instead of 122°). The product 4 is a bit more twisted than product 3 because the double bond in the 5-membered ring forces all the single bonds to be planar (incompatibility between sp2 and sp3 geometry). The Van der Wals's energy is more important in the product 3 because there is more hydrogen-hydrogen repulsion in this product (3 secondary carbon in a ring) than in the product 4 (2 secondary carbon in a ring). Finally, the product 3 is a bit more stretched because its double bond increases the bond length of the "bridge". The product 3 being less stable than the product 4, one can say that it wont be the major product of the hydrogenation.

Module 1: Part 2 : Intermediate in the synthesis of Taxol

The MM2 calculation for the "down" isomer gives a total energy of : 42.68 [kcal/mol]. The MM2 calculation for the "up" isomer gives a total energy of : 40.39 [kcal/mol]

According to ChemDraw, the "up" isomers is more stable. Those results are logical because the "up" product is less sterically hindered.

The hydrogenation of the double bond is slow because the resulting product would be very hindered. The calculation of the total energy of the saturated "up" isomer gives: 50.24 [kcal/mol]. The following table shows the detailed results.

Comparison between the "up" isomer and the hydrogenated product  :

Energy type	"up" isomer in [kcal/mol]	hydrogenated product in [kcal/mol]
Stretch	2.55	2.94
Bend	11.37	13.23
Stretch-Bend	0.32	0.57
Torsion	17.37	21.53
Non-1,4 VDW	-2.26	-1.39
1,4 VDW	12.74	15.11
Dipole/Dipole	-1.70	-1.75
Total Energy	40.39	50.24

The hydrogenation of the alkene bond is slow because this double bond is hyperstable. An alkene is hyperstable when the molecule obtained after the hydogenation is more hindered than the original molecule. When the hydrogenation occurs, the shape of the molecule will change because two carbons will have a sp3 geometry. If the molecule must struggle against steric constrains during the transformation, the activation energy will be important. Subsequently, the reaction will be less favorable (in a kinetic sens) and therefore, slower.

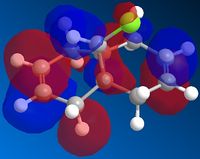
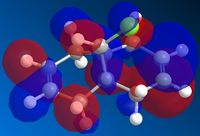
Module 1: Part 3 : Chloro-methanonaphtalene

The calculation of the molecular orbitals gave the following results (the results are not the same on two different computers): The first raw shows the orbitals calculated by the laptop and the second raw the orbitals calculated by the computer in the library.

HOMO-1	HOMO	LUMO	LUMO+1
HOMO -1 on the first computer	HOMO -1 on the first computer	HOMO -1 on the first computer	HOMO -1 on the first computer
HOMO -1 on the second computer	HOMO -1 on the second computer	HOMO -1 on the second computer	HOMO -1 on the second computer

The molecular orbitals calculated on the laptop are symmetric and then reflects the global symmetry of the molecule (plan of symmetry passing between the two double bonds and by the Cl atom).

The molecular orbital calculated on the computers in the library are not perfectly symmetric (particularly obvious for the HOMO and the LUMO). The fact that two computers (maybe two different versions of the software) don't give the same results suggests that the asymmetry must be caused by something related to the method of calculation and not by a chemical reason (the molecule is symmetric, the vibrations calculated on the SCAN are also symmetric then the MO should be symmetric).

The calculation of the IR spectrum gave the following result:

IR spectrum of the chloro-methanonaphtalene	IR spectrum of the hydrogenated chloro-methanonaphtalene
IR spectrum of the chloro-methanonaphtalene	IR spectrum of the hydrogenated chloro-methanonaphtalene

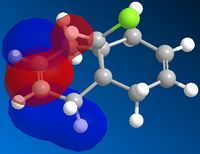
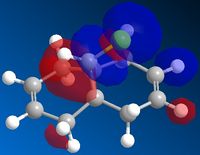
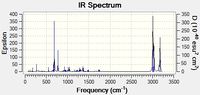
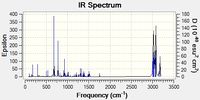
The second big peak (around 770 cm-1) is an important stretching of the Cl-C bond. This stretching is synchronized with a bending of the cyclopropyl ring - exo ring angle. The frequency of this vibration is relatively low because the reduced mass of the two atoms is big (Cl is heavy compared to C and H) and because the bond strength is small (only a sigma bond). In the original molecule (with two double bonds) the intensity of this peak is ~ 25. In the hydrogenated molecule, one can still observes this peak at the same frequency but this intensity is lower : ~ 20. This observation corroborates the hypothesis of an interaction between the HOMO on the exo ring and the LUMO of the Cl-C bond (this interaction decreases the angle between the cyclopropyl ring and the 6-membered ring). Effectively, when the exo double bonds is no longer there, the interaction doesn't exists and consequently the vibration intensity is lower. The interaction idea has been developed in the recommended article about this part of the module.

The alkene bonds vibrate with almost the same frequency (around 1737 cm-1 for the exo bond, around 1757 cm -1 for the endo bond). The frequency difference indicates that the endo bond is probably stronger (consequently electron richer and expressing a stronger alkene character) than the exo bond. This comment is compatible with the first observations (the HOMO-1 is delocalised, the exo bond has smaller orbital coefficient). In the hydrogenated molecule, the double bond vibration is still there, at the same frequency. One can deducts that the endo alkene bond is not really affected by the exo alkene bond. Therefor, the reactivity of the hydrogenated molecule will probably be the same.

Module 1: Part 1: glycosidation

1: In the molecule that is studied, the R group can be replaced by an hydrogen atom. This choice won't affect the glycosidation but will simplify the calculation. Here, the problem is to find the more stable conformer to know which isomer (α or β) will be created and to quantified the effect of the neighboring group participation. Clearly, the MOPAC/PM6 method is the best way to answer the question since it allows us to compare the heat of formation of the oxenium cation and of the intermidiates.

The four molecules (A, A', B and B') are the following:

A conformer	A' conformer	B conformer	B' conformer
A	A'	B	B'

2: The MM2 calculation gives the following results (total energy) for the A pair: A = 16.26 kcal/mol, A' = 15.59 kcal/mol and for the B pair: B = 16.58 kcal/mol, B' = 15.7 kcal/mol. In the two pairs, the stability difference can be explain by the conformation of the substituents on the ring. In each pair, the more stable isomer is the one that has all its substituents in axial position (instead of equatorial). This results are not what was expected. The MM2 method is based only on "classical" physics properties. In that case, the most stable structure should be the one in which all the substituents are in equatorial configuration (less hindered molecule). The fact that in an heterocycle the most stable configuration is sometimes the one in which the subsituents are in axial configuration in a purely quantum effect (orbital overlap, etc.) and then shouldn't be taken into account by the MM2 minimization. This effect should appear only with the MOPAC/PM6 method. Anyway, the energy differences given by the MM2 are relatively small and it's difficult to tell precisely which molecule is the most stable one.

3: The heats of formation calculated (using MOPAC/PM6) for the compound A,B,C and D are:

Heats of formation

Compound A	Compound B	Compound C	Compound D
-90.2 kcal/mol	-87.3 kcal/mol	-78.0 kcal/mol	-78.28 kcal/mol

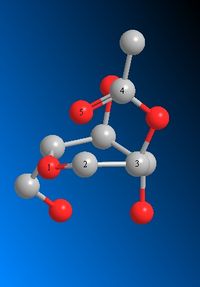
According to this results, the stabilization by neighboring group participation is weak . In the case of the couple B-D, the intermediate is stabilized of ~ 9 kcal/mol, for the A-C couple, the stabilization is ~12 kcal/mol. The energy values for each couple are closed because the MOPAC/PM6 minimization makes the oxenium cations and the intermediates look similar. The more interesting results are the comparison of the Ac group angles. The following table shows some of those angles:

Comparison of the angles in the molecules A and B processed by MM2 or MOPAC/PM6 method:

		A MM2	A MOPAC/PM6	B MM2	B MOPAC/PM6
Atoms serial number molecule A	1-2-5 angle	88°	105°	96.4°	105.7 °
Atoms serial number molecule B	2-3-4-5 angle	17.1°	1.6°	30.5°	-1.8°

This angles show that the MOPAC/PM6 method creates molecules that are closer to the "optimal" values. One can see that dihedreal angle (2-3-4-5) is, in the case of MOPAC, almost equal to 0. This means that the 4-5 double bond of the Ac group is aligned with the 2-3 single bond. In the same sens, the 1-2-5 angle is, with the MOPAC, is close to the value of an optimal 5-memered ring (pentagon) that is 108°-109°. As mentioned before, the oxenium cation optimized by the MOPAC and the intermediates are very resembling.

The MOPAC/PM6 method makes the molecules "tidier" and probably more energetically minimized than the MM2. Effectively, the MOPAC/PM6 method tends to set all the substituents in axial position (except for the molecule B). Consequently, the molecules minimized by the MOPAC method but in axial configuration must be lower in energy than the molecules minimized by the MM2 method but in equatorial configuration (because e.g. MM2 doesn't take into account the orbital overlap). Anyway, this affirmation should be qualified because it's difficult to compare directly the energies of the molecules processed by the two method since the type of result is different(steric energy for the MM2, heat of formation for the MOPAC/PM6).

4: The modeling of the oxenium cation and of the intermediates show the role of the neighboring group participation. In the intermediates, the acetate group forms a temporary 5-membered ring on the 6-membered ring . Then, it is obvious that the nucleophilic attack can not, for sterical reasons, take place on the side that is occupied by the acetate group.

Mini project:

The reaction that will be studied in the mini project is the last step of the reaction described in this article. The reaction is an aminocyclization that has a strong trans stereoselectivity. The authors of the article provide a list of different substituents that change the trans:cis relation.

In this part of the module, the computational modeling will be used to explain the stereoselectivity of the above-mentioned aminocyclization.

The expected reaction mechanism is the following:

Mechanism of the aminocyclisation

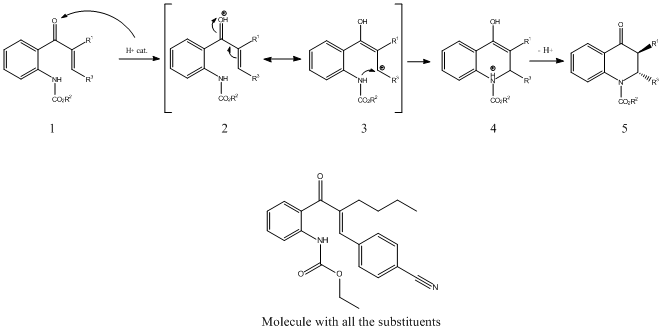It is said in the article that even with a "entgegen" starting reagent, the product is mainly trans. It means that the conformation of the molecule is decided during the reaction. The different steps of the reaction have been drawn and minimize using the MOPAC/PM6 method. The results are shown below:

Reaction step by step

Step 1	Step 2	Step 3	Step 4	Step 5
Step 1	Step 2	Step 3	Step 4	Step 5

In the three first steps, one can see that the position of R₁ and R₃ changes. In the starting molecule, the R₁ - R₃ bond is perpendicular to the aromatic ring. When the hydrogen attacks the ketone, the angle between th R₁ - R₃ bond and the aromatic ring decreases. The molecule reorganizes itself around the OH⁺ group. This is probably caused by a favorable interaction between the OH⁺ HOMO ans the butyl and ketone LUMO.

HOMO and LUMO of the step 2 molecule

HOMO	LUMO
HOMO	LUMO

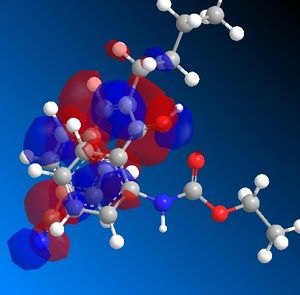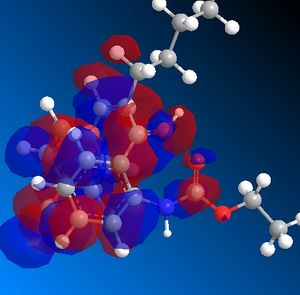This change in the molecule shape closers the nitrogen atom and the α carbon. In the step 1 molecule this distance is 5.3 [Å] long and in the step 2 molecule this distance is 4.8 [Å] long (according to MOPAC/PM6 calculation). The MM2 minimization gives different results : 5[Å] in the step 1 and 3.2 [Å] in the step 2.

In the step 3 molecule, the new double bond changes again the shape of the molecule but it is still impossible to see a factor that could promotes one conformation or the other. The N-αC distance is now 4.1 [Å] long (according to MOPAC/PM6 calculation) and 5[Å] long according to MM2 calculation.

In the step 4 molecule, the N-C bond is formed but the C=C double bond is still there. The MOPAC/PM6 optimized molecule has a non planar heterocyclic ring (this geometry doesn't appear in the MM2 optimized molecule). Because of the double bond, no particular conformation can be "chosen" by the molecule. The final shape of the molecule is then decided during the tautomerization of the enol. The MOPAC/PM6 calculation gives a similar heat of formation for the two isomers (cis and trans) (around -68.5 [kcal/mol] but a relatively different steric energy (22.3 [kcal/mol] for the trans isomer and 35.4 [kcal/mol] for the cis isomer). That could be an explanation of the trans selectivity of the reaction.

The C13 NMR spectrum won't be simulated because as said in the procedure, the simulation is highly sensitive to conformation of the molecules (the molecule studied here has a lot of possible conformation).

REFERENCES: