Rep:Mod:jl8913TS

Introduction

Computational chemistry gives the power to explain reactions and help predict new reaction outcomes as well as to give insight on how molecules behave, in essence allows the prediction of chemistry. Gaussian is one such program, based on the use of Gaussian orbitals. This allows the program to predict a wide number of molecular properties based on orbitals.

One such use for these programs is the predication of the transition state of reactions. Transition states are the saddle points of reactions, lowest energy pathway through the highest energy point of a reaction. This point of the reaction’s potential energy has a first derivative of 0 and a negative second derivative. This point is extremely difficult to observe due to the high energy nature of the structure resulting in a very short lifetime of this state ranging from 10^-12 to 10^-15 s. By calculating how atomic orbitals interact and the energy associated with the change in geometry, it is possible to create a theoretical transition state. These computational methods have a variety of levels of accuracy which is proportional to how computationally expensive, due to a more complex electron wave function relating to Slater determinants. By increasing the number of functions used to represent orbitals, a more accurate description is obtained due to the added flexibility of functions contribution but this however increases the calculation time. This particular experiment will look at using three different levels to describe the transition state of three different reactions and what factors influence the outcome of the transition state’s geometry. The different possible function combinations used in linear combinations are referred to basis sets .

Nf710 (talk) 10:27, 22 April 2016 (BST) Good understanding of the methods although DFT methods don't use slater determinants

This particular experiment uses Gaussian09W for calculations and GaussView 5.0 as a visualiser. This combination of programs allows for new molecules to be optimised and analysed with relative ease. This experiment will make use of the program to run optimisation, frequency, intrinsic reaction coordinate (IRC) calculations and to visualise molecular orbitals.

Cope Rearrangement

The Cope rearrangement is sigmatropic rearrangement of a 1,5-diene that produces a regioisomeric product that is also a 1,5-diene by thermal isomerisation. Typically the product formed is more thermodynamically favoured however in the particular example studied, both products are identical as the example is a 1,5-hexadiene. The reaction is expected to undergo a concerted bond rearrangement via a pseudo hexane ring proceeding by a chair or a boat transition state. By using computation methods, it is possible to ascertain which state is preferred and the magnitude of energy different of the two possible states.

Optimisation of 1,5-Hexadiene Conformers

HF/3-21G Optimisation

Figure 1. 1,5-hexadiene anti and gauche conformer

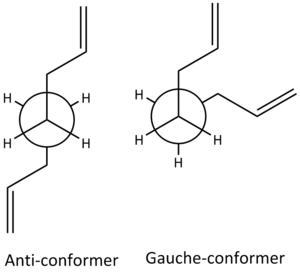
Initial optimisation used the HF/3-21G basis set on anti and gauche based conformers. Hartree-Fock calculations assumes that a wave function of a system can be approximated using a single Slater determinant . The current basis set used has 3 Gaussian functions to describe the inner shell orbitals, 2 Gaussian functions making up the first Slater type orbital (STO) of the double zeta where the double zeta allows treatment of each orbital separately and 1 function for the second STO . The anti-conformer has the two alkenes at a dihedral angle of 180^o and the gauche conformer has a dihedral angle of 60^o (see figure 1.).

Nf710 (talk) 10:30, 22 April 2016 (BST) Nice understanding of the orbitals

Table 1: Results of optimisation of 1,5-hexadiene conformers via HF/3-21G

Conformer	Optimised Structure	Energy, Hartrees / a.u.	Point Group	Log File
Gauche		-231.69254	C1	HF/3-21G anti.log
Anti		-231.69266	Ci	HF/3-21G gauche.log

Initially thoughts would lead one to think that the anti conformer would be more stable that the gauche conformer due to steric interactions. However computational calculations conclude that it is actually the gauche conformer (table 1.). This can be explained when examining the conformer's molecular orbitals.

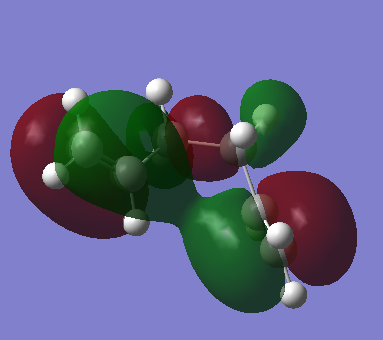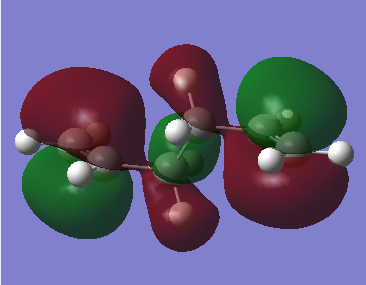
Figure 2. Gauche conformer HOMO molecular orbital	Figure 3. Anti conformer HOMO molecular orbital

From the two figures above. It is observed in gauche model, there is a $\pi$-$\pi$ orbital interaction with the two alkene groups as observed in the gauche HOMO molecular orbital. The anti conformer does not have this interaction due to the alkene groups being too far away from each other to provide a stabilising interaction due to the conformation of the molecule.

Nf710 (talk) 10:34, 22 April 2016 (BST) Nice use of the MOs to explain the ordering

B3LYP/6-31G(d) Optimisation

By using the previously Hartree-Fock optimised molecules, it is possible to further optimise them via use of a high basis set and a more advance computational method. One such commonly used method is B3LYP.

Becke, 3-parameter, Lee-Yang-Parr (B3LYP) is a commonly used hybrid functional. They are a class of approximations to the Density Functional Theory’s (DFT) exchange-correlation energy functional which uses Hartree-Fock theory and other theories to help improve the description of previously poorly described properties such as bond lengths and vibration frequencies .

The use of the 6-31G(d) basis set is also a more accurate and demanding computation model versus the previous calculation method used in the initial optimisation. As this basis set includes more Gaussian functions to model the orbitals of the molecule, giving greater accuracy.

By using a more accurate model the calculation time and computational power required is increased, though on current modern systems it is still feasible to run the calculations locally. On larger molecules this may not be possible and would possibly require access to a supercomputer or long period of calculation time.

Nf710 (talk) 10:34, 22 April 2016 (BST) Excellent understanding of B3LYP, it is indeed a hybrid type method

Table 2: Results of optimisation of 1,5-hexadiene anti conformer via B3LYP/6-31G(d)

Conformer	Optimised Structure	Energy, Hartrees / a.u.	Point Group	Log File
Anti		-234.61171	Ci	B3LYP/6-32G anti.log

The calculation retained the point group of the molecule however it differs to previously calculated HF/3-21G with a lower energy, however the energies of the two cannot be compared. This is due to the difference in density functional theory and Hartree-Fock methods of calculation of energy and the zero-point energy .

HF/3-21G and B3LYP/6-31G(d) Comparisons

Figure 4. Gauche conformer atoms labelling

Figure 5. Anti conformer atoms labelling

Table 3: Comparison of bond lengths of 1,5-hexadiene optimised via HF/3-21G and B3LYP-6-31G(d)

	Bond Lengths/ Å
Bond	HF/3-21G	B3LYP/6-31G(d)	Expected
C1-C2 (sp2-sp2)	1.31616	1.33351	1.340
C2-C3 (sp2-sp3)	1.50889	1.50421	1.504
C3-C4 (sp3-sp3)	1.55300	1.54830	1.541
C1-H8 (sp2-H)	1.07335	1.08684	1.085
C3-H11(sp3-H)	1.08475	1.09793	1.099

From table 3. t can be seen that compared to the Hartree-Fock method, B3LYP produced a longer bond length for C1-C2, C3-C4, C1-H8, C3-H11 and shorter bonds for C2-C3. By comparing the two sets of data to literature, using the B3LYP/6-31G(d) computation method produced bonds lengths closer to the expected values for 1,5-hexadiene. This is due to the increase level in accuracy in modelling of the molecule's orbital giving more detail on the bonding. While B3LYP method was more accurate under 1% difference from literature, the Hartree-Fock model still provided relatively accurate results with a variance with respects to literature of under 2%.

Table 4: Comparison of bond angles of 1,5-hexadiene optimised via HF/3-21G and B3LYP-6-31G(d)

	Bond angles/ o
Bond	HF/3-21G	B3LYP/6-31G(d)	Expected
H7-C1-C2	121.824	121.658	120
H11-C3-C2	109.971	109.748	109.5
C2-C3-C4-C5	179.991	179.998	180

Once again B3LYP produces results closer to the expected outcome however both still produced relatively accurate results. While both produce results close to literature, neither of the two computational models were able to obtain a dihedral angle (c2-C3-C4-C5) of 180^o though both are extremely close to the desire results.

There are several reasons for this outcome however they both stem from the fact that the B3LYP/6-31G(d) is a more accurate computational method. Firstly B3LYP is a DFT, which involves a greater number of parameters used in calculations. Secondly the 6-31G(d) basis set is a more accurate due to more Gaussian functions used for the Slater determinants . These also influence the accuracy of the bond angle and length.

Overall B3LYP/6-31G(d) produce more accurate results being closer to literature expected results compared to the HF/3-21G. Both produced acceptable results relative to literature.

Frequency Analysis on Anti B3LYP/6-31G Conformer

Figure 6. Computed IR spectrum of 1,5-hexadiene anti conformer optimised using B3LYP/6-31G(d)

The frequency calculations on the anti B3LYP/6-31G(d) optimised conformer showed no imaginary vibrations (negative values) and all vibrations obtained where positive and real. This means that the structure has been optimised to a minimum. B3LYP/6-32G anti Freq.log

An imaginary frequency is characteristic of a structure that is a possible transition state. It would be observed due to the second derivative of energy being negative representing a maximum if the first derivative is equal to 0, in other words the structure is at the height of a reaction coordinate energy graph.

$E=\hslash \omega (n+\frac{1}{2})$ Equation 1. Harmonic vibrational energy equation

• E, energy/ J; $\hslash$, Plank's reduced constant/ Js; $\omega$, vibrational frequency/ s^-1; n, quantum number

$\omega =\sqrt{\frac{k{f}_{}}{\mu }}$ Equation 2. Vibrational frequency equation

• $\omega$, vibrational frequency/ s^-1; k_f, force constant/ kgs^-2; $\mu$, reduced mass/ kg

Nf710 (talk) 10:35, 22 April 2016 (BST) very nicely formatted equations

By examining the above equations, it can be seen that if the second energy derivative was negative, the vibrational frequency must be as well. Since $\omega$ is proportional to the square root of k_f and reduced mass is always positive, the force constant must be negative causing an imaginary solution for $\omega$.

Thermodynamic Analysis

Another piece of data obtained from calculations are some thermodynamic energies relating to electronic and thermal energies.

Table 5: Thermodynamic energies of B3LYP/6-31G(d) 1,5-hexadiene anti conformer

Electronic energy type	Energy / a.u.
Sum of Electronic and Zero-point Energies (0 K)	-234.469214
Sum of Electronic and Thermal Energies (298 K)	-234.461865
Sum of Electronic and Thermal Enthalpies	-234.460921
Sum of Electronic and Thermal Free Energies	-234.500799

The sum of electronic and zero-point energies is the combination of both electronic potential energy and the zero point energy the system has, essentially the energy the system contains at 0 K. While the sum of electronic and thermal energies, is the sum of the energy components of translational, rotational, vibrational and electronic, effectively the energy of the system at room temperature and pressure. The final two energies from table 5. are the sum of electronic and thermal enthalpies and sum of electronic and thermal free energies. Both of these relate to thermodynamic equations relating to enthalpy and Gibbs free energy respectively. The thermal enthalpy energy includes the term RT while thermal energies contains an entropic term TS.

$H=E+RT$ Equation 3. Enthalpy equation

• H, enthalpy/ kJmol^-1; E, energy/ kJmol^-1; R, gas constant/ JK^-1mol^-1; T, temperature/ K

$G=H-TS$ Equation 4. Gibbs free energy equation

• G, Gibbs free energy/ kJmol^-1; H, enthalpy/ kJmol^-1; T, temperature/ K; S, entropy/ JK^-1mol^-1

Optimisation of Chair and Boat Transition State

Figure 7. Chair and boat conformer of cyclohexane

The transition state is believed to proceed via a concerted bond forming and breaking in either a cyclohexane like boat or chair conformation transition state. The preference of which geometry the transition state depends on the energy of the two states. By using computational methods, it is possible to 'optimise' to a transition state geometry.

Optimisation of Chair Transition State

A chair structure is one of the two possible conformers of of cyclohexane. Traditionally it is viewed as the lower energy conformer versus the boat conformer. The chair conformation has prefect sp³3 bond angles and experiences no torsional strain. While the transition state in this particular experiment also involves carbon double bonds altering the geometry from the ideal cyclohexane structure, general principles of the cyclohexane chair conformation can still be used to understand this particular transition state. However the main difference will the bond lengths and bond angles due to the carbon atoms being in a pseudo sp²/sp³ centre due the presence of double bonds.

Optimisation of Allyl Fragment

The transition state can be broken up into two identical allyl fragments that undergo concerted bond formation and breakage during the transition state.

Table 6: Results of optimisation of allyl fragment via HF/3-21G

Optimised Structure	Energy, Hartrees / a.u.	Point Group	Log File
	-115.82304	C2v	Allyl fragment.log

With the optimised structure two methods were used to try to obtain the chair transition state. One method involved making education guesses using the TS Berny method during optimisation and another involved fixing the distance between certain atoms while using the same TS Berny method.

Optimisation of 1,5-hexadiene's Chair Transition State via use of TS Berny Method at HF/3-21G theory, guess method

The previously optimised allyl fragments were used to build the transition state. This was achieved by placing one fragment on top of another at a distance of approximately 2.2 Å from the terminal carbons and in a 'ring-like' structure. In addition to the change in calculation method, the force constant was changed to be calculated once and additional key word 'opt=noeigen' was used to prevent the calculation crashing.

Table 7: Results of optimisation of 1,5-hexadiene chair transition state via TS Berny Method and HF/3-21G, guess method

Optimised Structure	Energy, Hartrees/ a.u.	Imaginary Frequency/ cm-1	Log File
	-231.61932	-817.89	Chair transition state guess method.log

The calculation as predicted, form a chair-like structure for the transition state. It can also be observed that the carbon atoms are all in an intermediate hybridisation between sp³ and sp², seen by the carbon bonds on the allyl fragments comprising of a pseudo bond order of 1.5. This is due to the formation and breakage of carbon double bonds occurring simultaneously with the transition state being when the process is only halfway through.

Figure 8. Animation of imaginary frequency of chair transition state at -817.89 cm-1, guess method

The optimised structure produced a vibration with a negative frequency of -817.89 cm^-1. This single imaginary frequency helps prove the newly optimised structure is a transition state as explained previously. The vibration describes the transient breakage and formation of the C-C bonds. It can be seen in figure 8. that one end of the allyl fragment has the breakage of the C-C bond as the formation of the new C-C bond on the other end of the structure occurs, a concerted action as previously expected.

Optimisation of 1,5-hexadiene's Chair Transition State via use of TS Berny Method at HF/3-21G theory, frozen bond method

Another method involving the optimisation of the chair transition state is to 'freeze' the terminal carbon atoms at a set distance of 2.2 Å. This particular distance is the distance where the carbon bonds form and break. By freezing this distance, is will hopefully force the calculation to optimise the desire transition state.

Table 8: Results of optimisation of 1,5-hexadiene chair transition state via TS Berny Method and HF/3-21G, frozen bond method

Optimised Structure	Energy, Hartrees/ a.u.	Imaginary Frequency / cm-1	Log File
	-231.61932	-817.90	Chair transition state frozen bond method.log

The structure once again is similar to the expected chair-like structure, containing properties that are extremely similar to the previous outcome with the guess method. This is to be expected since both should if are correctly used and set up, produce the same transition state.

Figure 9. Animation of imaginary frequency of chair transition state at -817.90 cm-1, frozen bond method

Once again an imaginary frequency was observed at -817.90 cm^-1. It should be noted both methods produce essentially identical results both in terms of the vibrational frequency and energy of the structure. This is due to both methods ultimately optimise to the same chair structure and use the same calculation model to achieve this. As such the vibrational frequency shows the same concerted bond formation and breakage at the terminal carbon atoms as previously seen with the guess method.

Table 9: Comparsion of bond lengths of the chair transition state of 1,5-hexadiene via HF/3-21G and TS Berny using either guess or frozen bond method

Bond type	Guess method bond length/ Å	Frozen bond method bond length/ Å
Average allyl carbon-carbon bond	1.38923	1.38922
Average terminal carbon-carbon distance	2.02067	2.02042

From the bond lengths certain mechanistic ideas can be inferred. One of type of bond formation and breakage is due to a C=C double bond. This can be inferred due to the length of the allyl bonds being an intermediate between a C=C double bond and a single bond. By using a similar logic, the longer terminal carbon bond is relating to a single bond forming and breaking between the two carbon atoms, as the bond length is an intermediate length of a carbon-carbon single bond and two carbon van der Waals radii (1.70 Å per carbon).

As seen in table 9., both methods also produce similar bond breakage and formation lengths. While both are acceptable methods in producing the transition state, if knowledge is known about the transition state structure the frozen method is superior. Due to the ability to incorporate some data about the transition state into the calculation. While the guess method is more useful if little is known about the transition state structure, as it easier to set up a new structure to run another calculation by use of the visualiser to displace the fragments.

Optimisation of Boat Transition State

The boat conformation of cyclohexane has typically a higher energy versus its chair conformation brother. This is due to the boat conformer experience torsional strain due to the non-prefect sp³ carbon centres. The conformer also experiences steric interactions from 'flagpole' hydrogens within two van der Waal radii. However as previously mentioned, this particular transition state is not a prefect cyclohexane boat conformer but one based around having carbon atoms at a hybridisation that is an intermediate of sp³ and sp². This once again is expected to cause variation from the cyclohexane model that the transition state is believed to be based on.

Optimisation of 1,5-hexadiene boat Transition State via use of QST2 method at HF/3-21G theory, start end method

Figure 10. Reactant (1) and Product (1) structure for 1,5-hexadiene boat transition state optimisation via QST2

This particular method of calculations made use of QST2 method. QST2 is a Synchronous Transit-Guided Quasi-Newton (STQN) method, this employs the use of either a linear synchronous transit or quadratic synchronous transit to optimise the molecule close to the quadratic region of the transition state and then finishes the optimisation with a quasi-Newton based algorithm. . This particular method uses two inputs, a reactant and product. By using the two structures as required for a QST2 (the two species the number of molecules), the method will try to converge to a transition state from the two molecules which therefore does not require a transition state structure.

Table 10: Results of optimisation of 1,5-hexadiene boat transition state via QST2 Method and HF/3-21G, start end method

Optimised Structure	Energy, Hartrees/ a.u.	Imaginary Frequency / cm-1	Log File	Image of Transition State
	-231.61932	-817.89	Boat transition state QST2 method.log	Figure 11. Optimisation of 1,5-hexadiene boat transition state via QST2 Method and HF/3-21G, incorrect optimisation

Figure 12. Reactant (1) and Product (1) structure for 1,5-hexadiene boat transition state optimisation via QST2, altered geometry

While a transition state was formed, it was incorrect in regards to what was desired. A chair-like transition state with data similar to the previously optimised chair transition state but a difference from the previous results are the transient bonds from the terminal carbons to the opposite end of the other allyl fragment. This can explained by examining the input structures. Due to the calculation seeing that the terminal atoms end up bonded together and the centre C3-C4 bond broken, it computes the lowest energy transition state (chair) and forcibly cuts and forms intermediate bonds to obtain the desire product.

Therefore to force the calculation to optimise to a boat transition state, the inputs must be changed to reflect this. This is achieved by changing the dihedral angle from 180^o to 0^o (figure 12.). This is to make the mechanism for the rearrangement more obvious for the calculation method, due to C1 and C6 being in line to form a bond as well as the structures look more appreciable with regards to a chair conformation.

Table 10: Results of optimisation of 1,5-hexadiene boat transition state via QST2 Method and HF/3-21G, start end method

Optimised Structure	Energy, Hartrees/ a.u.	Imaginary Frequency / cm-1	Average allyl C-C bond length/ Å	Average terminal C-C distance/ Å	Log File
	-231.60280	-840.02	1.38147	2.14005	Boat transition state QST2 method.log

The newly optimised transition state formed the desire boat conformation and the bond breakage and formation occurring in the correct manner. Quick analysis confirms previous believes that the boat is a higher energy conformer with this mirror in the transition state energy on comparison with the chair conformation.

Figure 13. Animation of imaginary frequency of boat transition state at -840.02 cm-1 using QST2 method

This is also reflected in the imaginary frequency obtained which once again, was a singular occurrence. However on comparison to the chair's vibration, the boat has a more negative valve. This could be because as a higher energy vibration due to a higher energy transition state causing bond formation and breakage to occur at a higher energy compared to the chair transition state previously calculated.

Intrinsic Reaction Coordinate (IRC) of Chair and Boat Transition State Structure at HF/3-21G

One method to confirm the optimisation formed a transition structure is to preform a IRC calculation. This calculation calculates the energies of a structure and tries to optimise it to form either the reactant or product, whereby the energy is minimised. The theory being that the transition structure is at the energy maximum on the reaction coordinate therefore any and all further optimisations reduces the energy of the structure till either the starting molecule or product is formed.

Table 11. Graphs displaying results of IRC; Total energy of molecule against reaction coordinate; Energy gradient against reaction coordinate of the transition structure of 1,5-hexadiene

Chair	Boat
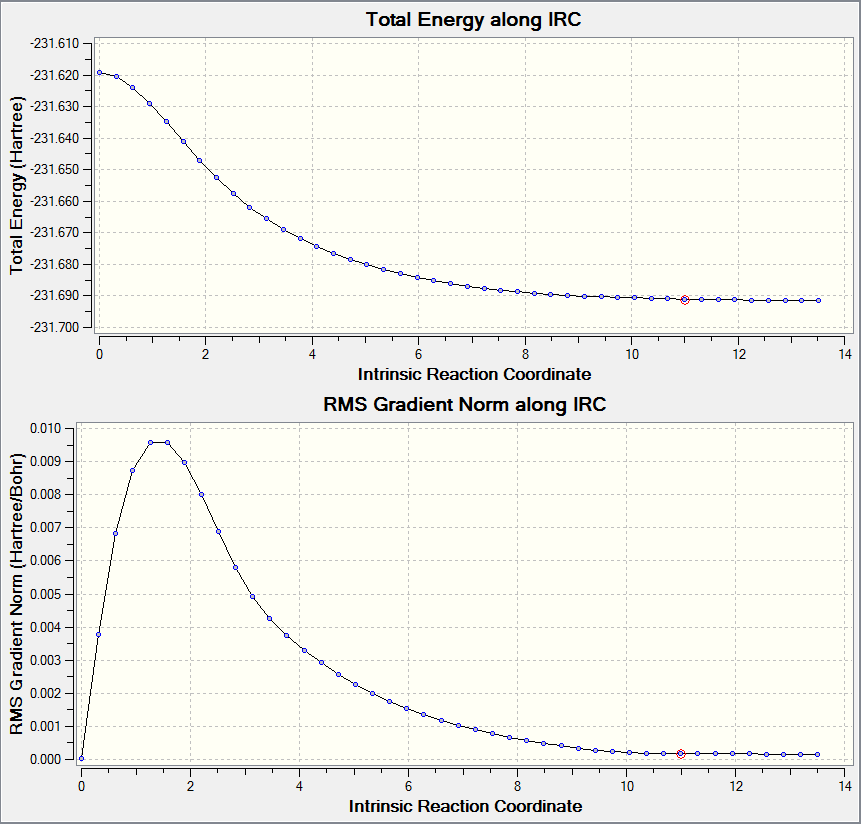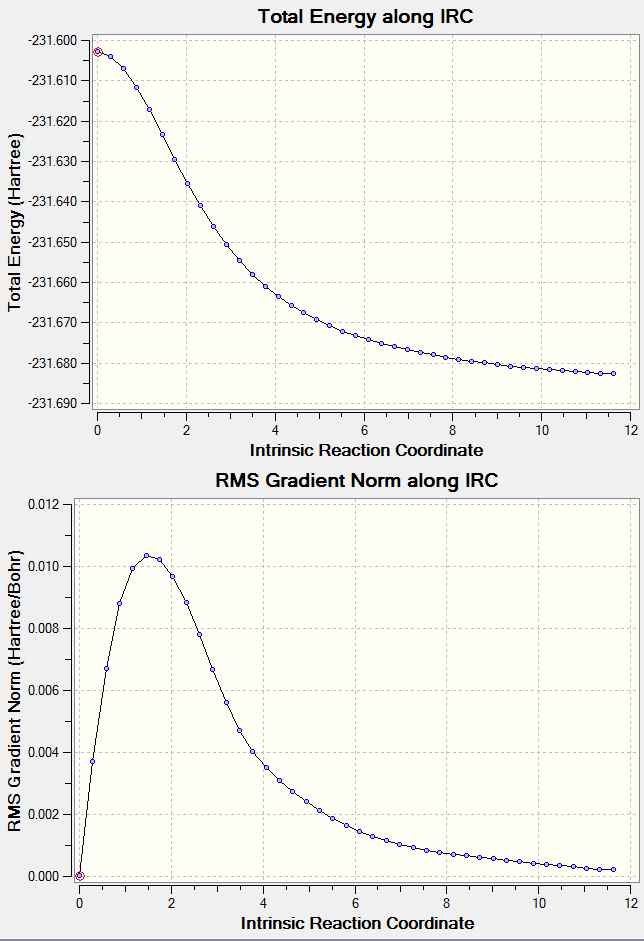
Chair transition state TS Berny method IRC.log	Boat transition state QST2 method IRC.log

The main result seen from the graph is that the initial steps in the reaction coordinate do not have an optimised structure higher in energy compared to the starting point. From this set of results, the previously calculated structures are indeed the transition state structures desired.

This particular instance, only the forward direction for IRC was calculated due to the product and reactant being the same compound which should give a symmetrical results. However for other systems, it would be preferred to preform both directions as they would not likely be symmetrical around the transition state.

Optimisation of 1,5-hexadiene's Transition State at B3LYP/6-31G theory

Table 12: Results of optimisation of 1,5-hexadiene transition state at B3LYP/6-31G

Conformer	Optimised Structure	Energy, Hartrees/ a.u.	Imaginary Frequency / cm-1	Average allyl C-C bond length/ Å	Average terminal C-C distance/ Å	Log File
Boat		-234.54309	-530.36	1.39323	2.20664	Boat transition state at B3LYP/6-31G.log
Chair		-234.55365	-565.54	1.47050	1.96755	Chair transition state at B3LYP/6-31G.log

Once again the boat transition structure has a larger relative energy versus the chair structure and both structures contained a single imaginary frequency, demonstrating that a transition structure has been formed.

Figure 14. Animation of imaginary frequency of chair transition state at -565.54 cm-1 using B3LYP/6-31G	Figure 15. Animation of imaginary frequency of boat transition state at -530.36 cm-1 using B3LYP/6-31G

Previous calculation as at a lower computational level obtained results that described the imaginary frequency for the boat to be a more negative value. However the B3LYP/6-31G calculation show the opposite to be true.

Both Hartree-Fock and Density Functional Theory based calculation methods achieved the same geometry for the both conformers, showing that both calculation levels produce no difference in structure.

Thermodynamic Results of Transition State Structure Optimisation

Table 13: Comparsion of thermodynamic energies of chair, boat transition state and reactant at both HF/3-21G and B3LYP/6-31G calculation levels

	Energy, Hartree/ a.u.
Conformer	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.46670	-231.46134	-234.55698	-234.41493	-234.40901
Boat TS	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39601
Reactant (anti2)	-231.69254	-231.53954	-231.53257	-234.61171	-234.46921	-234.46187

The energy of the reactant is lower compared to the two transition state and the boat transition state is higher energy state compared to the chair conformer for both calculation model. These results are expected from previous intuition and reasons stated earlier relating to torsional strain and steric hinderance.

Table 14: Comparsion of activation energies for the chair and boat and reactant at both HF/3-21G and B3LYP/6-31G(d) calculation levels

	Energy/ kcalmol-1
Conformer	HF/3-21G		B3LYP/6-31G(d)		Experimental
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE(Chair)	45.70713	44.69496	34.06433	33.16762	33.5 ± 0.5
ΔE(Boat)	55.60357	54.76020	41.96278	41.32586	44.7 ± 2.0

While both computational models produce accurate looking geometry, the energy of the two models are vastly different. The B3LYP/6-31G(d) produced results more accurate when compared to experimental results. This is due to DFT based calculation being more accurately describing the electronic structure of the atoms . In fact the B3LYP/6-31G(d) calculations almost within or in certain instances within the experimental range of accepted results.

Nf710 (talk) 11:01, 22 April 2016 (BST) Veryy good report, you have done everything asked of you and you have looked at the theory and gone beyond the script and read further than expected. well done.

Diels Alder Cycloaddition

Diels Alder reaction is when a conjugated electron rich diene reacts with a molecule with an elctron deficient dienophile to form a new cyclic molecule with two new sigma bonds formed via lost of two pi bonds . The necessity of the diene being electron rich and the dienophile being electron poor stems from the relative energies of their HOMO and LUMO. An electron rich high lying HOMO and an electron poor low lying LUMO facilitates a small energy gap, this allows for a better orbital interaction which in turn aids the progression of the reaction. Another requirement for the reaction is that the diene must be a s-cis conformation to allow for a concerted reaction.

These reaction will be examined using the semi-empirical molecular orbital calculation method, AM1. The semi-empirical method reduces the computational effort required by approximately certain variables which are calculated in an Hartree-Fock calculation. This is achieved by only considering valence electrons in the system and the core electrons are assumed part of the nuclear core . The semi-empirical method is therefore used as a cheap method to optimise a guess structure before using a more expensive method such as B3LYP to calculate an accurate structure.

Diels Alder Cycloaddition - Cyclohexene

The simplest example of a Diels Alder reaction is one with ethene and butadiene to form cyclohexene (figure 16.). This reaction is essence a [4+2] cycloaddition.

Optimisation of butadiene via use of AM1 theory

Cis-butadiene in this particular reaction is our conjugated diene. The cis conformer is optimised due to the reaction requiring a cis conformation for orbital interaction.

Table 15: Results of optimisation of cis-butadiene via AM1

Optimised Structure	Energy, E(RAM1) / a.u.	Point Group	Log File
	0.048797	C2v	cis-Butadiene AM1.log

Due to the difference in the method of energy calculation a positive energy was calculated for the optimised molecule versus an expected negative energy as produce in previous methods.

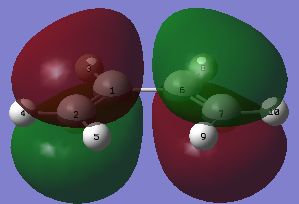Figure 15. Butadiene HOMO	Figure 16. Butadiene LUMO

From the figures above (figure 15, 16.) it can be observed that the HOMO is antisymmetric with respects to the plane of the molecule, LUMO is symmetric again with respects to the plane of the molecule.

It can be seen that the electron density is centred around the π bonds in the HOMO. This is expected, as carbon double bonds are electron rich. The LUMO shows that there is a bonding interaction between the carbon single bonds if there is additional electron density added to that site, also the double bonds would break on addition of electron density which is the expected outcome of a Diels Alder reaction.

Optimisation of ethene via use of AM1 theory

Ethene acts as our dienophile in this particular experiment.

Table 16: Results of optimisation of ethene via AM1

Optimised Structure	Energy, E(RAM1) / a.u.	Point Group	Log File
	0.026190	D2h	Ethene AM1.log

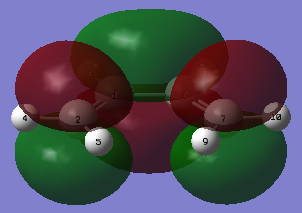
Figure 17. Ethene HOMO	Figure 18. Ethene LUMO

In this instant with ethene, the HOMO is symmetric and LUMO is antisymmetric with respects to the plane of the molecule. From the MO images, it can be infer that with addition of electron density, the carbon double will break into single bonds.

Optimisation of ethene and butadiene Diels Alder transition structure via AM1

Cyclohexene is the expect product of a Diels Alder reaction between the two starting material, cis-butadiene and ethene. The transition structure was calculated by using a method based on the previously used 'guess' method. This was carried out by aligning the two reactants at a distance of 2.2 Å between the terminal carbons with a geometry that mimics a cyclohexane.

Table 16: Results of optimisation of ethene and butadiene Diels Alder transition structure via AM1

Optimised Structure	Energy, E(RAM1) / a.u.	Imaginary Frequency/ cm-1	Log File
	0.11165	-956.40	Ethene and butadiene Diels Alder transition structure AM1.log

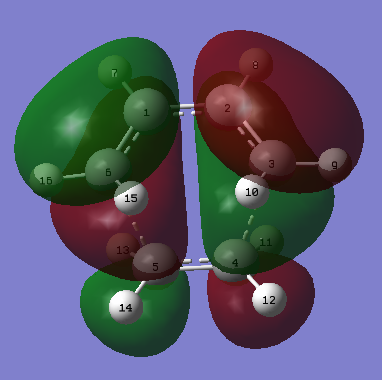Figure 19. Ethene and butadiene Diels Alder transition structure HOMO	Figure 20. Ethene and butadiene Diels Alder transition structure

The energy of the newly optimised structure is of a larger magnitude to its components and there is a presence of one imaginary frequency, both of these factors leads to the belief that a transition structure is formed.

Initial information gained from the MO images (figures 19, 20.) is that the HOMO of the transition structure is antisymmetric and the LUMO is symmetric with respects to the plane of the transition structure.

Another piece of information that can be gathered is which molecular orbitals were used to form the transition state HOMO and LUMO. The HOMO of the transition state is comprised of the ethene's LUMO and butadiene's HOMO both of which are antisymmetric. The LUMO is therefore comprised of the ethene's HOMO and butadiene's LUMO and both of the orbitals are symmetric. This gives arises to Woodward-Hoffman rule, where there is a π⁴ and π² component. These components react in a suprafacial manner (same face).

$(4q+2{)}_s+(4r{)}_a$ Equation 3. Woodward-Hoffman equation for determining thermally allowed cycloaddition reactions

• (4q+2)_s, suprafacial component; (4r)_a, antarafacial component

By solving equation 3. for this particular reaction, q is equalled to 1 and r is 0. This gives a sum that is odd which according to Woodward-Hoffman rules, the reaction is thermally allowed.

From these molecular orbital images, it can be inferred that the electron density from cis-butadiene's π bonds are interacting with ethene's π anti-bonding orbital causing the double bond to break. Also the π bond's electron density from ethene is causing the formation of a π bond on the butadiene which also interacts with the butadiene's alkene anti-bonding orbital, causing breakage.

Figure 21. Animation of imaginary frequency of ethene and cis-butadiene transition state at -956.40 cm-1, AM1 method

These observations are further backed up when examining the vibrational mode of the singular imaginary frequency of the structure which also infers transition state formation.

Figure 22. Animation of the lowest positive vibration of ethene and cis-butadiene transition state at 147.24 cm-1, AM1 method

Figure 23. Cyclohexene formation transition structure with labelled atoms calculated at AM1

From figure 22., it can be seen that this particular frequency does not correlate to any bond formation nor to any breakage. This is due to the vibration does not involve any of the fragments to move towards nor away from each other, which is indicative of a change in bond order. Instead the vibration at this frequency correlates to the fragments 'flexing'. The reason for this is since the imaginary frequency occurs at the saddle point of the reaction pathway, so in either the forward or backwards direction of the reaction coordinate will cause bond formation and breakage since the saddle point represents the transition state. Therefore any other vibrational frequencies will not contain a vibrational mode involving the change on bond order.

(Good paragraph here Tam10 (talk) 18:22, 7 April 2016 (BST))

Table 17: Bond lengths of the transition structure of the cycloaddition reaction between ethene and cis-butadiene at AM1

Bond	Bond Lengths/ Å	Bond type
C1-C2	1.39741	Intermediate; single/double
C2-C3	1.38189	Intermediate; single/double
C3-C4	2.11907	Intermediate; single/twice van der Waals
C4-C5	1.38293	Intermediate; single/double

By comparing bonds lengths of the transition structure to literature and the van der Waals radius of carbon, the type of bond formation and breakage can be inferred (table 17.). As two van der Waals radii for carbon is 3.40 Å, a sp² C=C is 1.35 Å and a sp³ C-C bond is 1.54 Å.

Graphs displaying results of IRC; Total energy of molecule against reaction coordinate; Energy gradient against reaction coordinate for the formation of cyclohexene from ethene and cis-butadiene at AM1 method

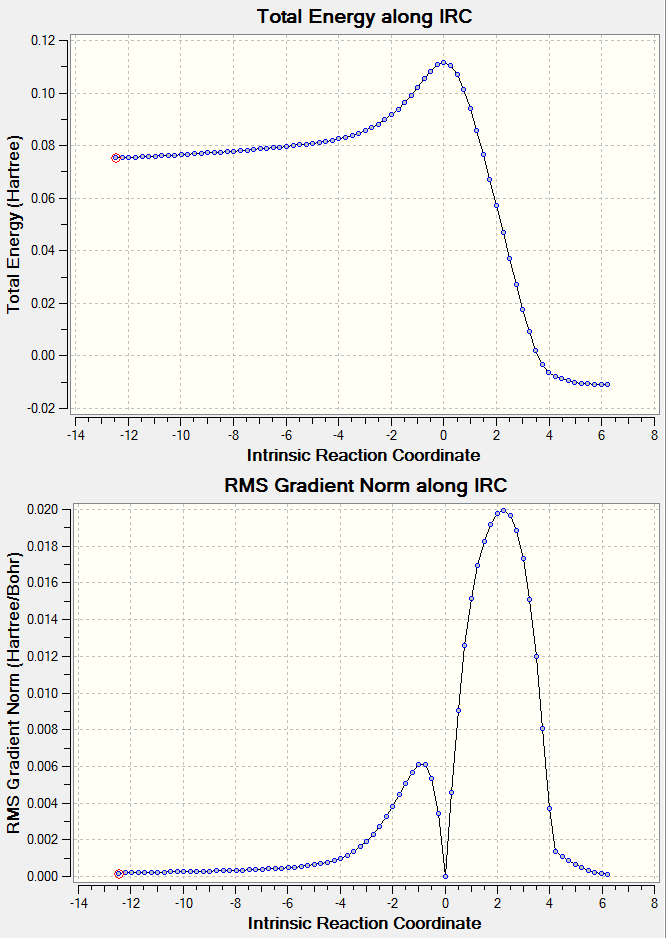		Ethene and butadiene Diels Alder transition structure IRC AM1.log
Figure 24. Results from IRC calculations on transition structure of ethene and cis-butadiene reaction

The IRC calculation help prove that the transition structure was formed due to the same reasons as mention previously for the experiments about the Cope rearrangement. It can be seen that the overall reaction is predicted to be exothermic. This phenomenon does occur during physical experimentation, sometimes produce an unexpected large amount of heat.

Diels Alder Cycloaddition - Regioselectivity

Some Diels Alder reactions have a selectivity issue where there is two possible products, an endo and exo product. This is possible with the reaction with cyclohexa-1,3,diene with maleic anhydride. However since the reaction is kinetically controlled, the endo product dominates due to the lower energy of the transition structure. This particular experiment will look to see if this is the case by using computational methods.

The method to examine the transition structure will be the QST2 method which requires an input for the reactant and product molecule.

Optimisation of cyclohexa-1,3-diene using AM1

Cyclohexa-1,3-diene acts as the diene for the Diels Alder reaction.

Table 18: Results of optimisation of cyclohexa-1,3-diene via AM1

Optimised Structure	Energy, Hartrees / a.u.	Log File
	0.0277711	Cyclohexa-1,3-diene at AM1.log

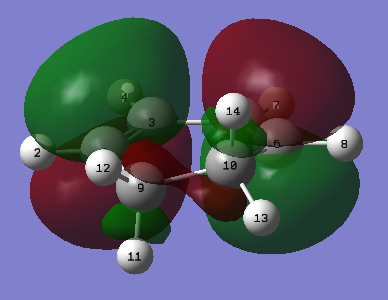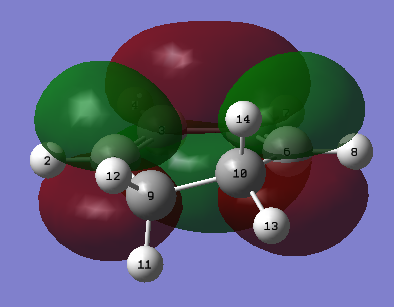
Figure 25. Cyclohexa-1,3-diene HOMO	Figure 26. Cyclohexa-1,3-diene LUMO

Once again the MO diagram depicts the sites of the alkenes to be in a bonding interaction at the HOMO and the LUMO shows on addition of electron density, the two C=C bonds would break to from a C=C bond.

Optimisation of maleic anhydride using AM1

Maleic anhydride is a dienophile in this particular reaction.

Table 19: Results of optimisation of cyclohexa-1,3-diene via AM1

Optimised Structure	Energy, Hartrees / a.u.	Log File
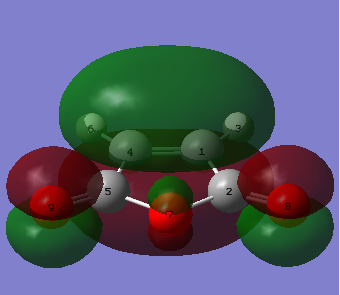
	-0.12182	Maleic anhydride at AM1.log

Figure 26. Maleic anhydride HOMO	Figure 27. Maleic anhydride LUMO

The molecular orbital images simulate the for the HOMO where electron density is locate via orbial overlap between atoms. The LUMO describes the change in the bond order with addition of electron density during the Diels Alder reaction.

Optimisation of endo transition state

Table 20: Results of optimisation of endo transition structure via AM1

Optimised Structure	Energy, Hartrees / a.u.	Relative energy, Hartrees / a.u.	Imaginary Frequency	Log File
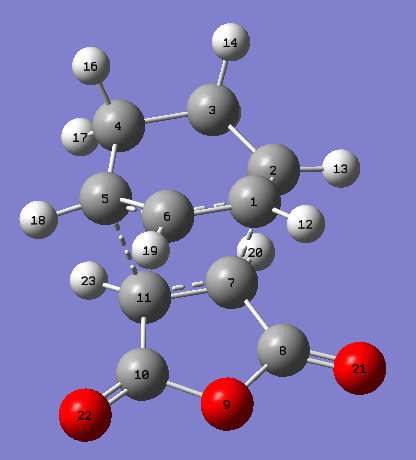
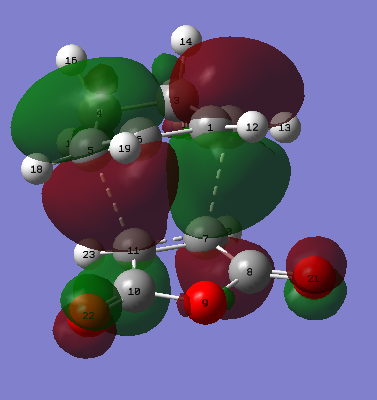
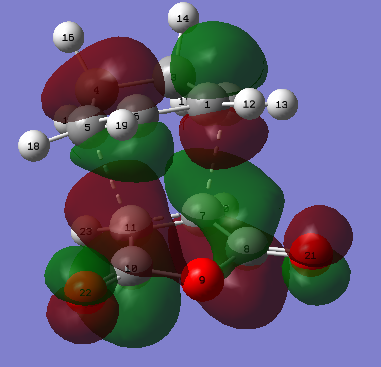
	-0.051505	0.0	-806.40	Endo product at AM1.log
Figure 28. Endo product atoms labelled	Figure 29. Endo product HOMO	Figure 30. Endo product LUMO

Figure 31. Animation of the imaginary frequency of the endo product at -806.40 cm-1, AM1 method

The bond formation is described by figure 31., the vibration of the imaginary frequency and via the MO images. Where there is two suprafacial components forming each forming a sigma bond between the two molecules. There is also the breakage of C=C bonds on the maleic anhydride and on the cyclohexadiene as seem by anti-bonding orbitals in the HOMO where originally the C=C bond resided.

Table 21: Bond lengths of the endo transition structure, AM1

Bond	Bond length/ Å	Bond type
C1-C2	1.39305	Intermediate; single/double
C1-C6	1.39725	Intermediate; single/double
C2-C7	2.16246	Intermediate; single/twice van der Waals
C7-C11	1.40849	Intermediate; single/double

The previous observations with regards to the change of bond order is further cemented with the bond length data (table 21.). The bond type assignment was done by taking into account of the bond length of single, double and two carbon van der Waal radii. The fact that all bonds involved with the mechanism are of an intermediate length shows the concerted nature of the reaction.

Optimisation of exo transition state

Table 22: Results of optimisation of exo transition structure via AM1

Optimised Structure	Energy, Hartrees/ a.u.	Relative Energy, Hartrees/ a.u.	Imaginary Frequency	Log File
	-0.050420	0.0010848	-812.19	Endo product at AM1.log
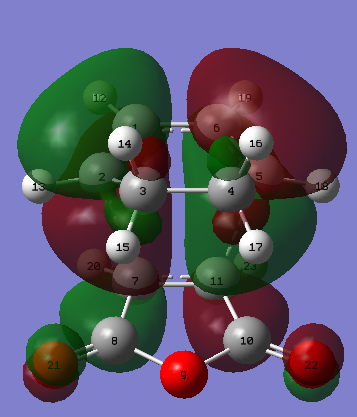
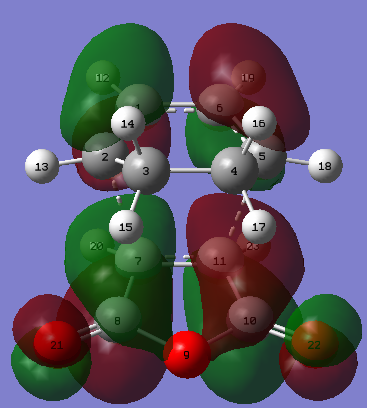
Figure 32. Exo product atoms labelled	Figure 33. Exo product HOMO	Figure 34. Exo product LUMO

Figure 35. Animation of the imaginary frequency of the exo product at -812.19 cm-1, AM1 method

Table 23: Bond lengths of the endo transition structure, AM1

Bond	Bond length/ Å	Bond type
C1-C2	1.39438	Intermediate; single/double
C1-C6	1.39676	Intermediate; single/double
C2-C7	2.17040	Intermediate; single/twice van der Waals
C7-C11	1.41011	Intermediate; single/double

Similar findings can be made with the exo transition state which were made with endo transition state. As ultimately both undergo the same reaction however what changes is the geometry and therefore the energy. This discussion however is made below.

Endo versus Exo transition state

The endo transition structure is more stable than the exo by 0.0010848 a.u. which is 2.84814 kJmol^-1 (0.68072 kcalmol^-1). This could be due to the extra steric hindrance provide by the exo's hydrogen groups on the C3 and C4 position. As these centres are formerly sp³ versus the endo equivalent carbons C6 and C1 which are formerly before reaction sp². These two carbon centres affect the energy of the state due to their hydrogens being within van der Waals distance (3.40 Å) with the maleic anhydride carbon C10 and C8 which causes steric clash. This is more apparent with the sp³ carbons due to by nature of the geometry of the molecule is force to have one hydrogen point down towards the maleic anhydride. This is little concern with a sp² due to the hydrogen being in the plane of the molecule.

While both experience good primary orbital overlap at the bonding atom sites, there is oewever another factor that makes the endo transition structure the preferred pathway. The secondary π orbital overlap effect between C=O and C=C groups . This interaction is only possible for the endo structure due to geometric restrictions prevent the exo structure to achieve good orbital overlap. With access to this effect, the endo structure is more stabilised during the transition state thereby lowering its energy.

Conclusion

The use of Gaussian and GaussView is a powerful tool, allowing the optimisation of molecule's structure and even transition structure with a variety of methods to do so. Allowing for calculations for more general analysis or expensive, detail and powerful methods

The Cope rearrangement had a preferred transition structure of the chair conformer due to less sterics and torisonal strain present. It was also observed that while both HF and B3LYP methods produces very similar geomteries, the energy calculations were different.

Experiments on the Diels Alder reaction demonstrated that the preferred conformation to cross the saddle point is the endo structure. This is due to less sterics between the maleic C-O-C with CH-CH versus the exo which had interactions of C-O-C with CH₂-CH₂.