Rep:Mod:jl8013

Introduction

In this experiment the transition structures of large molecule were studied using computational methods. Transition structures, reaction paths and barrier heights were all calculated. Firstly the Cope Rearrangement, followed by a simple and then more complex Diels Alder cycloaddition. The results can be used to examine the nature of the mechanisms for each reaction as well as the energy requirements.

The Cope Rearrangement

The Cope rearrangement is a concerted, [3,3]-sigmatropic shift, in which a 1,5-diene is thermally isomerised into a regioisomeric 1,5-diene. In this experiment the cope rearrangement of 1,5 -hexadiene was computed. The objective was to to locate the low-energy minima and the transition structures on the potential energy surface, in order to determine the preferred reaction mechanism.

Fig.1 Cope Rearrangement

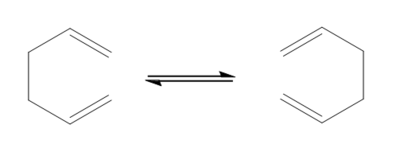
It is generally accepted that this reaction occurs via either a ‘chair’ or ‘boat’ transition structure, the ‘chair’ being lower in energy. By computation methods, using the program gaussian, this hypothesis was tested.

Fig.2

Optimizing the Reactants and Products

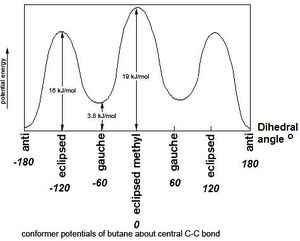
Gauche vs Anti

Using Gaussview a molecule of 1,5-hexadiene was constructed with an antiperiplanar linkage across the four central carbon atoms. This was optimized using the Hartree Fock method and a basis set of 3-21G. This produced Structure 1, with an energy of -231.6926 a.u. (Log). The molecule displays 180 degree rotational symmetry and its point group is C2. As per [Appendix 1], this structure is the low energy conformer Anti 1.

Then a molecule of 1,5-hexadiene was constructed with an gauche linkage across the four central carbon atoms. This was optimized using the Hartree Fock method and a basis set of 3-21G. This produced Structure 2, with an energy of -231.6915 a.u. ( Log). The molecule displays 180 degree rotational symmetry and its point group is C2. As per Appendix 1, this structure is the low energy conformer Gauche 4.

It is usual to calculate activation energies and enthalpies using the lowest energy conformation as a reference. Steric theory would suggest that an anti conformation would be the lowest energy structure (see Fig.3), as in anti conformation there is the least steric hindrance due to overlap of the substituents.This is confirmed by the two structures produce above. However in their paper, "Conformational Study of 1,5-Hexadiene and 1,5-Diene-3,4-diols", Gung, Zhu, and Fouch actually suggest that a particular gauche confirmation is the lowest in energy. This is due to the fact that "an attractive interaction may be present between the pi orbital and the vinyl proton." This conformer (Structure 3) was constructed and optimized in Gaussian ( Log). It was found to have an energy of ...This structure corresponds with Gauche 3, as found in the appendix, which is the lowest energy conformer given.

Nf710 (talk) 23:40, 4 November 2015 (UTC) You coudl have actually proved this yourself. if you had looked in the chk file and looked in the orbitals you would have seen with the gauce3 there is actually in phase orbital overlap with the two double double bonds lowering the energy of the molecule.

Fig.3

Name	Structure	Energy/Hartrees HF/3-21G	Relative Energy/Kcal/mol	Point Group	Conformer
Structure 1	View Structure	-231.6926	0.04	C2	Anti 1
Structure 2	View Structure	-231.6915	0.71	C2	Gauche 4
Structure 3	View Structure	-231.6927	0.00	C1	Gauche 3

Anti 2 Conformer

The C_i Anti 2 conformer was then constructed and optimized at the HF/3-21G level, giving an energy of -231.69254 a.u ( Log). (equivalent to that given in Appendix 1). The structure was then further optimized to the B3LYP/6-31G* level. This gave a structure with an energy of -234.61171 a.u. ( Log) These different levels of theory resulted in subtle changes in geometry, but with no pattern to the changes. These are detailed in the table below. The geometry seen in the B3LYP/6-31G* level of optimization is lower in energy.

Nf710 (talk) 23:43, 4 November 2015 (UTC) You cant compare HF and DFT methods, they have completely different hamaltonians. So it is meaningless to compare them.

(number as per Fig.4)	Energy/ Hartrees	1,4,6,9-dihedral bond angle /degrees	1,4 bond length/ angstroms	4,6 bond length/ angstroms	6,9 bond length/ angstroms
HF/3-21G	-231.69254	114.667	1.316	1.509	1.553
B3LYP/6-31G*	-234.61171	118.600	1.334	1.504	1.548

Fig.4 Anti 2 Numbering

A frequency calculation was then carried out on the B3LYP/6-31G* optimized Anti 2 structure ( Log), this allows for the computed energy values to be compared with experimentally obtained values. This also allows for the critical point to be characterized. All the vibrational frequencies reported were real and positive showing that a minimum had been reached. The computed energies can be seen below.

	computed values/ a.u.
sum of electronic and zero-point energies	-234.469215
sum of electronic and thermal energies	-234.461867
sum of electronic and thermal enthalpies	-234.460922
sum of electronic and thermal free energies	-234.500800

Optimizing the "Chair" and "Boat" Transition Structures

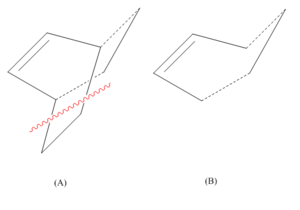
The ‘chair’ and ‘boat’ transition structures were then optimized. In both structures the terminal ends of the reactants are known to be approximately 2.2 angstroms apart.

Chair

A guess chair transition structure was created by drawing a C3H5 allyl fragment and optimizing it to HF/3-21G (Log). This fragment was then copied and the two fragments placed in an approximate chair transition structure, about 2.2 angstroms away from each other at their terminal ends. As seen below.

Chair TS Guess

This guess transition was then optimized using two techniques (at all times using HF/3-21G). Optimizing a transition state is more difficult than a minimum as the negative direction of curvature must be known. This is done, providing a reasonable guess for the transition state is used, by computing the Hessian initially and updating it as the optimization proceeds.

Nf710 (talk) 10:23, 5 November 2015 (UTC) Nice use of Jmol and good knowledge of the hessian. Its basically a matrix of second order derivatives (force constants in this case)

Berny Optimization

For this operation the guess transition state must be very close to the actual transition state, however it is able to optimize to the transition state using only one structure. The guess structure was run giving the structure seen below (Log). An imaginary frequency of magnitude 818.00 cm^-1 (see Fig.5) was obtained corresponding to the Cope Rearrangement.

Frozen Coordinate Method

In this method the terminal ends of the guess fragments were held in their starting positions, 2.2 angstroms apart. The reaction coordinate was then frozen, and the rest of the molecule optimized to a minimum (Log). Once at a minimum, but with the terminal ends in a transition state position, the reaction coordinate was unfrozen and the transition state optimized. This can help save valuable time as the entire Hessian does not need to be computed, rather by differentiating along the reaction coordinate a reasonably guess for the original Hessian can be made. When this optimization was run the transition state seen below was produced (Log), with an imaginary frequency of a very similar 117.89 cm^-1

Vibration	Frequency/cm-1	Terminal-Terminal Length /Angstroms	Energy/Hartrees
Berny Optimization Transition State	818.00	2.01992, 2.02033	-231.6193
Frozen Coordinate Vibration	117.89	2.02074	-231.6028

Both transition state optimizing methods gave a terminal-terminal length of around 2.2 angstroms. However The Berny Optimization gave two slightly different values showing that it is slightly less accurate than the frozen coordinate method. However the difference between the two values is minimal and the ease of the Berny method still makes it a viable method for transition state optimization.

Nf710 (talk) 10:27, 5 November 2015 (UTC) Your berny is correct but you seem to have found the wrong local minimum for this optimization it should have the same vibrational frequency as you are optimising to the same thing

Boat

A boat transition structure was then produced and optimized using the QST2 (or Synchronous Transit-Guided Quasi-Newton) method. In this method, rather than providing a guess transition structure both the reactant and the product must be given. This method is fully automated but requires the reactants and products to be close to the transition state. The atoms in the two structures must be identical so that the calculation can interpolate between the two structures until it finds the transition state. The optimized Anti 2 molecule, produced previously, was used for both the product and reactant and positioned as per Fig.5

Fig.5 QST2 Initial Boat Reactant and Product

When it was run this method failed, producing the structure seen in Fig.6 (Log). This is clearly far from the actually transition state. The QST2 method is simple and so merely translated one of the allyl fragments rather than rotating about the central bonds. In order to produce an accurate transition state with this method the reactants and products must start much closer to the transition state.

Fig.6 QST2 Failed Boat TS

In order to do this the geometry of the structures had to be changed. The dihedral angle of the central four carbons, of both products and reactants, was reduced to zero degrees and the angle between the pair of three inside carbons was changed to one hundred degrees. This gave the reactant and product structures seen in Fig.7.

Fig.7 QST2 Geometry Changed Boat Reactant and Product

The QST2 optimization was then run on the new structures giving the transition state shown below (Log). There is an imaginary frequency of magnitude 840.13 cm^-1 shown below. The transition structure had an energy of -231.60280 a.u.

Boat Transition State Vibration

Nf710 (talk) 10:30, 5 November 2015 (UTC) well done for shoing how you got the boat, the vibrational frequency is correct

IRC

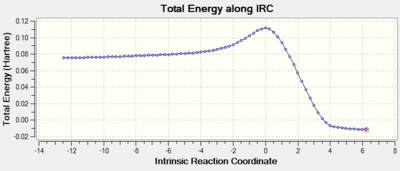
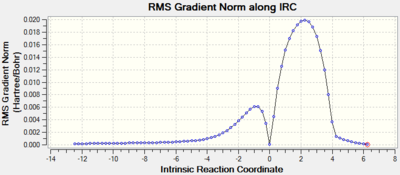
In order to prove that the desired transition state has been achieved the reaction path (that is the minimum energy path from the transition state to product or reactant), must be followed in both directions to its minima. This allows for the conformers of 1,5-hexadiene that correspond to the reactants and products to be found, which would otherwise be impossible. This process is called an 'Intrinsic Reaction Coordinate' (IRC). It works by moving away from the transition state in a sequence of constrained geometric optimizations, down the minimum energy path. In this example the IRC was run for the optimized chair transition structure. This was done only in the forward direction since the reaction coordinate was symmetrical. This gave the plots seen below. (Log)

It can be seen that the energy starts at a maximum, the optimized chair TS seen above. Then with gradual steps the structure changes until it reaches a minimum. The minimum structure (see Fig.8) has an energy of -231.692 a.u., this is the structure referred to as gauche 2 in Appendix 1.

Fig.8 IRC minimum - Gauche 2

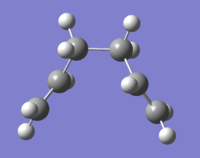
Nf710 (talk) 10:31, 5 November 2015 (UTC) correctly run IRC and correctly identified the conformer that it connects

Activation Energies

The final aim of these calculations is to calculate the activation energy for the Cope Rearrangement. In order to do this both the chair and boat transition states must be optimized to a higher level of theory using the B3LYP/6-31G* method and then frequency calculations carried out. When the higher level of optimization is compared to the lower one there are minimal geometry changes. However the energy differences are noticeable. (Chair Log, Boat Log)

	HF/3-21G			B3LYP/6-31G*
(All energies in Hartrees)	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K
Chair	-231.61932237	-231.466697	-231.461338	-234.55693104	-234.414908	-234.408980
Boat	-231.60280240	-231.450934	-231.445305	-234.54307817	-234.402350	-234.396007

(All at 0 K in Kcal/mol)	HF/3-21G	B3LYP/6-31G*	Expt.
ΔE (Chair)	45.94	34.34	33.5 ± 0.5
ΔE (Boat)	56.31	43.07	44.7 ± 2.0

From these results it can be seen that the B3LYP/6-31G* method is far more accurate than the HF/3-21G method. It also shows that the more advanced level of computational theory is incredibly accurate as an approximation for the actually energy of the transition state. Values for the chair and boat at B3LYP/6-31G* are within or close to the experimental value given.

Nf710 (talk) 10:53, 5 November 2015 (UTC) Your energies look correct However you havent included the anti 2 conf or the temperatures at 298K. You have correctly deduced that for geometries as smaller basis set can be used. But for energies to get close to experiment you need to be using a larger basis set.

10:53, 5 November 2015 (UTC) In all you have show a good general understanding of the basic principles of computational chemistry. It would have been nice if you have related the second derivative force constant to the k in the quantum vibrionic oscillator equation and hence this is where we get the imaginary frequency from as you are rooting a negative number. Good attempt

The Diels Alder Cycloaddition

The Diels Alder reaction is a [4+2]-cycloaddition of a conjugated diene and a dienophile. It involves the formation of two new sigma bonds from the four pi electrons of the diene and the two pi electrons of the dieneophile. The formation of sigma bonds, which are more stable than pi bonds, is the driving force behind the reaction. In this reaction the HOMO/LUMOs of the two reactants interact to form two new bonding MOs and two new antibonding MOs. If the HOMO of one reactant and the LUMO of another can interact then the reaction is said to be allowed. However if due to different symmetries the overlap density between the LUMO and HOMO is insufficient the reaction will not occur. The energy of the LUMO and HOMO that are interacting must be close in energy in order for the reaction to proceed. Electron-withdrawing substituents on the dieneophile lower the energy of the LUMO facilitating the reaction. Similarly dienophile substituents with pi orbitals are able to interact with the double bond which is formed in the reaction, this acts to stabilize the regiochemistry of the reaction. In this exercise the nature of the transition structures of two different Diels Alder reactions were computed, a prototypical reaction and one where both reactants carry substituents and secondary orbital effects are possible. In all these cases the Semi-empirical AM1 method was used to reduce time and costs when computing larger molecules.

Fig.9 Ethylene+Butadiene cycloaddition

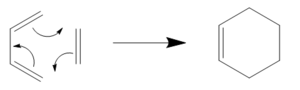
Ethylene+Butadiene cycloaddition

In this reaction the pi/pi* orbitals of the ethylene and the HOMO/LUMO of the butadiene are interacting in a [4s + 2s] reaction. By plotting the HOMO and LUMO of the reactants at their transition structure the nature of the reaction can be analysed.

Cis-Butadiene

A cis-Butadiene molecule was construed on Gauss View and the geometry optimized (Log). The HOMO and LUMO were plotted and can be seen below.

	HOMO	LUMO

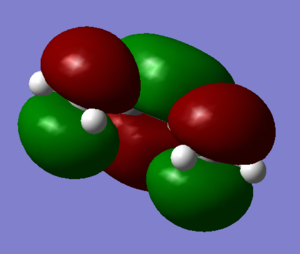The HOMO of Cis-Butadiene is shown to be antisymmetric with respect to the plane and the LUMO symmetric.

Ethylene+Butadiene Transition State

The transition structure for this reaction has an envelope type structure, this allows for the maximization of the ethylene pi orbital and butadiene pi system overlap. In order to create this, a bicyclic system was created, as in Fig.10. This was done by creating a cyclohexene structure (Log) and an ethylene structure (Log) separately and optimizing both structures. From the cyclohexene the -CH2-CH2- fragment was then removed, and the two fragments placed together. The method used to optimize this structure was the Berny Optimization, this reduced the time required to produce the transition structure. However the interfragment distance must be close to the actual value for this to successfully optimize to the transition structure. In the paper "Ethylene-Butadiene Diels-Alder Reaction " it is suggested that this distance is 2.2 angstroms. This distance was used and the transition state was optimized successfully (Log).

Fig.10

It can be confirmed that a transition state was reached as the structure had one imaginary frequency of magnitude 955.91 cm^-1, seen below. The vibration shows that the two new C-C bonds are synchronous. In comparison the lowest positive vibration (see below) is asynchronous. The concerted reaction seen in the transition state is in agreement with the 'allowed' orbital interaction.

(Your imaginary frequency should be written as -955.91 cm^-1 or i955.91 cm^-1. However, it's clear what you mean. Note that reaction won't take place through the positive frequency. Tam10 (talk) 11:02, 28 October 2015 (UTC))

Ethylene+Butadiene Transition State	Ethylene+Butadiene lowest positive Vibration

(Excellent use of Jmols Tam10 (talk) 11:02, 28 October 2015 (UTC))

An IRC, in both directions, was also run to ensure that a transition structure had been reached (Log). The plots can be seen below. It is clear that at reaction coordinate zero the energy is at a maximum, the transition state. The energy then drop to a minimum in both directions. In the negative direction the less stable reactants and in the positive direction the more stable product.

	Transition State	Reactants	Products
Structure
Relative Energy/Kcal/mol	76.96	54.18	0.00

The geometry of the transition structure can be seen below. All of the original bonds are now similar in length, at a length between a double and a single bond. This shows that at the point of the transition state the electron density is almost evenly spread across the fragment. The interfragment length is clearly smaller than twice the Van der Waals radius of a carbon atom. This shows that there is a positive interaction between the terminal carbons and that a sigma bond will be formed there.

	Typical sp3	Typical sp2	VDW radius of C	C1-C4	C11-C7	C7-C9	C9-C14	C1-C11	C4-C14
Bond Length/ Angstroms	1.54	1.34	1.70	1.383	1.382	1.400	1.382	2.119	2.119

HOMO	LUMO

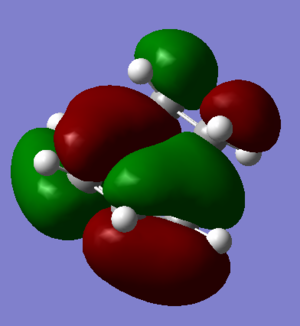The HOMO and LUMO of the transition state can be seen above. The HOMO is antisymmetric with respect to the plane and the LUMO symmetric. In order to form the HOMO of the transition state the HOMO of cis-Butadiene and the LUMO of ethylene (see Fig.12) have been used. Both are antisymmetric and therefore since they have the same symmetry have significant overlap density and the reaction is able to occur.

Fig.12 Ethylene LUMO

Cyclohexa-1,3-diene + maleic anhydride Cycloaddition

The reaction between Cyclohexa-1,3-diene and maleic anhydride is a facile, regioselective cycloadition. The reaction can produce either an endo or exo adduct (see Fig.13), however the endo product predominates.

Fig.13

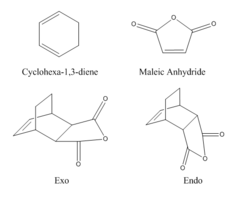
In order to produce the transition states, Cyclohexa-1,3-diene and maleic anhydride were constructed separately and optimized. They were then positioned as close to the transition state as possible. The QST2 method was used. The transition states were used as the reactants. Then the endo and exo products were constructed and optimized and used as the products in the QST calculation. The computation was run and successfully produced a transition structure for both endo (Log) and exo (Log) products.

	Guess TS	Product	TS
Endo
Exo

Vibrations

It can be confirmed that a transition state was reached for both endo and exo as the structures had one imaginary frequency each. For Endo one of magnitude 806.40 cm^-1 and for Exo one of magnitude 812.74 cm^-1, seen below.

Endo Transition State	Exo Transition State

Energies

(Energies in Hartrees)	Electronic energy	Sum of electronic and zero-point energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Activation Energy at 0 K /Kcal/mol
Endo	-612.68339574	-612.502207	-612.491836	27.7
Exo	-612.67933542	-612.498004	-612.487667	28.5

These results show that the Exo transition state is higher in energy than the Endo. Hence the activation energy for the Exo product is higher than for the Endo. This shows that the reaction must be kinetically controlled since experiments show that the Endo product predominates.

Geometries

(Bond Length/Angstroms)	partly formed σ C-C	C-C - [(C=O)-O-(C=O)- -CH2-CH2-/-CH=CH-]
Endo	2.162	2.892
Exo	2.171	2.945

Other than the obvious structural differences in the two structures their geometries are similar. All C-C bond distances in both structures are almost equal. There is a very slight difference in the partially formed sigma bonds, although this is too small to be of consequence. The C-C distance between the carbons of the (C=O)-O-(C=O) fragment and the -CH2-CH2- for Exo and -CH=CH- for Endo are noticeably different however. In the Endo form there are secondary orbital interactions between the pi systems of -CH=CH- and (C=O)-O-(C=O) fragment. These secondary orbital interactions are interactions between orbitals not directly involved in the creation of new bonds. These orbitals produce a slight bonding interaction between the the (C=O)-O-(C=O) fragment and the -CH=CH- fragment. Although these interactions don't result in any new bonds they act to lower the energy of the transition state. Literature suggests however that these secondary orbital interactions are not alone responsible for the higher relative stability of the Endo product . In the Exo form there is steric repulsion between the the -CH2-CH2- fragment and the maleic anhydride, due to the sp3 nature of the carbons. The positive secondary orbital interactions of the Endo form along with the steric repulsion in the Exo form accounts for the lower relative stability of the Exo transition structure and hence the Endo preference of the reaction despite the greater stability of the Exo Product.

Orbitals

	HOMO	LUMO
Endo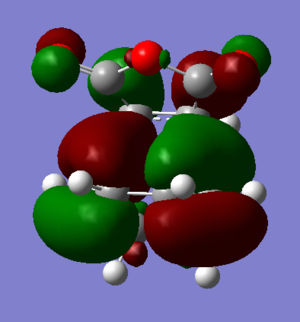
Exo

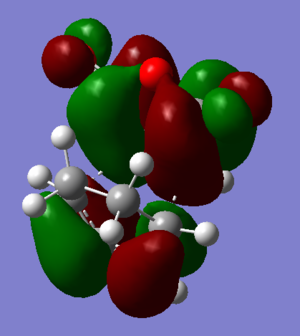The HOMO of the Endo product shows that there would be a slight positive bonding interaction between the -(C=O)-O-(C=O)- fragment and the opposite -CH=CH- fragment. This is in agreement with the conclusion above. However the orbitals on the -(C=O)-O-(C=O)- fragment are very small, this shows that the interaction is minimal although it could also be due to the simple semi-empirical AM1 method used to optimize the TS. When optimized to a higher level of theory a more accurate depiction of the orbitals would be available. Since the secondary orbital effect is so weak a higher level of theory thus seems necessary.

Conclusion

In this experiment it has been shown that it is possible to compute transition states to an acceptable level of accuracy to compare with, and give a guide towards, experimental data. The transition structure for both the Boat and Chair transition of the Cope Rearrangement were found. The computation showed that the activation energy of the chair route was lower and hence more favorable. Although the HF/3-21G method wasn't particularly accurate the B3LYP/6-31G* method gave results that were almost exactly in agreement with experimental values, showing the legitimacy of using computational techniques to calculate such values. The transition structures of two Diels Alder reactions were also computed, between Ethylene and Butadiene, and between Cyclohexa-1,3-diene and maleic anhydride. It was shown that by plotting computed molecular orbitals the reactivity of the reactants and the geometry of the products can be explained. Generally the lower AM1 method was used in order to keep time and costs low, however comparison with experimental values showed that at least a level of theory of B3LYP/6-31G* is required for accurate results. With more time all of the calculations could have been computed at higher levels of theory to give more accurate energy values, geometries and depictions of molecular orbitals.