Rep:Mod:jl5810mod3

The Cope Rearrangement

Optimising Reactants and Products

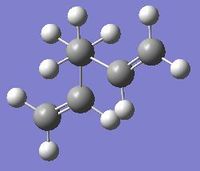
The image on the right shows the Cope rearrangement, and it can be seen that both the reactant and product are 1,5-hexadiene. In order to investigate the reaction, firstly the various conformers of 1,5-hexadiene are optimised with the Hartree Fock method at the 3-21G level of theory, and the structures symmetrised to find the point groups. The different structures are based around either an anti-periplanar conformation, in which the central 4 carbon atoms have a dihedral angle of 180^o, or a gauche conformation, in which the central 4 carbon atoms have a dihedral angle of 60^o.

Anti-Periplanar 1 Conformation

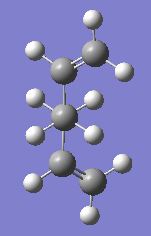
The anti-periplanar 1 conformation is on the right, the symmetrise function shows the point group to be C₂.

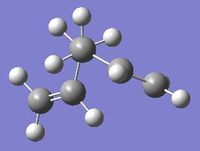
Gauche 1 Conformation

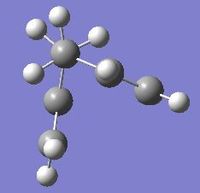
The gauche 1 conformation is on the left, the symmetrise function shows the point group to be C₂.

Summary of All Possible Conformations

The following table views the structures like Newman projections to help differentiate the possible conformations of 1,5-haxadiene, and summaraises the energies and point groups of each. It also provides the logfiles for each optimisation. Firstly the structures were optimised as above, using the HF/3-21G level, and then the DFT-B3YLP/6-31G* level is used to reoptimise each structure.

Conformer	Newman Projection	Point Group	3-21G level		*6-31G level**		logfile
Conformer	Newman Projection	Point Group	Energy/Hartrees	Relative Energy/kcal/mol	Energy/Hartrees	Relative Energy/kcal/mol	3-21G level	*6-31G level**
Gauche 1		C₂	-231.68772	3.10	-234.60788	2.46	File:1 5 HEXADIENE GAUCHE HF 3 21G OPT.LOG	File:1 5 HEXADIENE GAUCHE DFT 6 31G OPT.LOG
Gauche 2		C₂	-231.69167	0.62	-234.61068	0.70	File:1 5 HEXADIENE GAUCHE2 HF 3 21G OPT.LOG	File:1 5 HEXADIENE GAUCHE2 DFT 6 31G OPT.LOG
Gauche 3		C₁	-231.69266	0.00	-234.61133	0.29	File:1 5 HEXADIENE GAUCHE3 HF 3 21G OPT.LOG	File:1 5 HEXADIENE GAUCHE3 DFT 6 31G OPT.LOG
Gauche 4		C₂	-231.69153	0.71	-234.61052	0.80	File:1 5 HEXADIENE GAUCHE4 HF 3 21G OPT.LOG	File:1 5 HEXADIENE GAUCHE4 DFT 6 31G OPT.LOG
Gauche 5		C₁	-231.68962	1.91	-234.60911	1.69	File:1 5 HEXADIENE GAUCHE5 HF 3 21G OPT.LOG	File:1 5 HEXADIENE GAUCHE5 DFT 6 31G OPT.LOG
Gauche 6		C₁	-231.68916	2.2	-234.60889	1.82	File:1 5 HEXADIENE GAUCHE6 HF 3 21G OPT.LOG	File:1 5 HEXADIENE GAUCHE6 DFT 6 31G OPT.LOG
Anti 1		C₂	-231.69260	0.04	-234.61180	0.00	File:1 5 HEXADIENE APP HF 3 21G OPT.LOG	File:1 5 HEXADIENE APP DFT 6 31G D OPT.LOG
Anti 2		C_i	-231.69254	0.08	-234.61171	0.06	File:1 5 HEXADIENE APP2 HF 3 21G OPT.LOG	File:1 5 HEXADIENE APP2 DFT 6 31G D OPT.LOG
Anti 3		C_2h	-231.68907	2.25	-234.60962	1.37	File:1 5 HEXADIENE APP3 HF 3 21G OPT.LOG	File:1 5 HEXADIENE APP3 DFT 6 31G OPT.LOG
Anti 4		C₁	-231.69097	1.06	-234.61079	0.63	File:1 5 HEXADIENE APP4 HF 3 21G OPT.LOG	File:1 5 HEXADIENE APP4 DFT 6 31G OPT.LOG

The Hartree-Fock method describes the energy and motion of the electrons by a single-particle function by solving the time-independent Schrodinger equation, which predicts the molecular orbitals. This, however, does not depend on the interactions between electrons or their instantaneous motion.^[1] The DFT, or density functional theory method however includes the electron correlation energy, and as part of the B3LYP (Becke's 3-parameter exchange functional with the correlation functionals of Lee, Yang and Parr) includes part of the Hartree Fock exchange as well, giving an improved estimation of the energy of each conformation.^[2] It can be seen that using the DFT-B3LYP/6-31G* lowers the enrgies of the anti-periplanar conformations more than the gauche, however the overall order remains the same. This would make sense as the HF method does not take account of the increase in electron repulsion when the pi bonds are closer together in the gauche conformations.

Frequency Analysis and Thermochemistry

A frequency analysis of the anti periplanar 2, c_i, conformation is carried out at the DFT-B3LYP/6-31G* level to cofirm a minimum energy has been found, and to gain a more in depth analysis of the energies. These include the zero point energy, the potential energy with the ZPE (E = E_elec + ZPE), the sum of the electronic and thermal energies, including the rotational, translational and vibrational energies (E = E + E_vib + E_rot + E_trans). Also the sum of the electronic and thermal enthalpies (H = E + RT) and the sum of the electronic and thermal free energies (G = H - TS) are given.

Here is a link to the logfile for the frequency analysis File:1 5 HEXADIENE APP2 DFT 6 31G D FREQ.LOG.

There are no negative vibrations in the frequency analysis, which shows a minimum has been found. 1 negative frequency shows a transition state has been found, and more than one shows the frequency analysis has failed. A summary of the thermochemistry is shown here.

 Zero-point correction=                           0.142507 (Hartree/Particle)
 Thermal correction to Energy=                    0.149853
 Thermal correction to Enthalpy=                  0.150797
 Thermal correction to Gibbs Free Energy=         0.110933
 Sum of electronic and zero-point Energies=           -234.469204
 Sum of electronic and thermal Energies=              -234.461857
 Sum of electronic and thermal Enthalpies=            -234.460913
 Sum of electronic and thermal Free Energies=         -234.500777

The frequency analysis is run again with the temperature set to 0.001K, instead of the standard 298.15K in all calculations unless otherwise stated. 0K would have been used, however GaussView would just run the calculation t 298.15K when 0K was specified. The following summary shows the energies are all equal to the electronic energy plus the ZPE, as there are no thermal contributions at 0K.

Zero-point correction=                           0.142507 (Hartree/Particle)
 Thermal correction to Energy=                    0.142507
 Thermal correction to Enthalpy=                  0.142507
 Thermal correction to Gibbs Free Energy=         0.142507
 Sum of electronic and zero-point Energies=           -234.469204
 Sum of electronic and thermal Energies=              -234.469203
 Sum of electronic and thermal Enthalpies=            -234.469203
 Sum of electronic and thermal Free Energies=         -234.469203

Here is a link to the logfile for the frequency analysis at 0KFile:1 5 HEXADIENE APP2 DFT 6 31G OPT FREQ 0K.LOG

Optimising the Chair and Boat Transition States

The cope rearrangement goes through a transition state which could be viewed as two CH₂CHCH₂ allyl fragments joined by partial bonds between each terminal carbon, as shown below.

Reaction pathway for the Cope rearrangement showing the transition state.

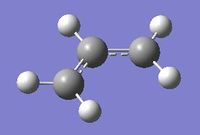
We can optimise a structure for one of these allyl fragments, and then combine two in the correct orientation in order to make a guess at the transition states for the reaction. The fragment is optimised at the HF/3-21G level for now in order to make the processes quicker, however when the transition states have been found they can be optimised at a higher level.

Here is a link to the logfile for the optimisation File:ALLYL HF 3 21G OPT.LOG

Chair Transition State

The following diagram shows how the transition state can have two structures, a "chair" or a "boat". By orientating the two allyl fragments to look like one of these we can make a guess at the transition state and then optimise it.

Chair (left) and boat (right) transition state structures.

The guess is made to look like the chair transition state, with the allyl fragments about 2.2A apart. An opt+freq analysis is run, with the "Optimization to a TS (Berny)" option selected, the force constants calculated once and the Opt=NoEigen keyword used.

Here is a link to the logfile for the opt+freq analysis File:CHAIR TS HF 3 21G OPT FREQ.LOG

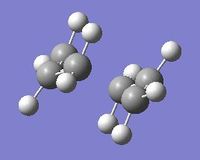
The optimised structure has the fragments 2.02A apart, the one negative frequency at -818cm^-1 corresponds to the breaking and formation of the single bonds between the two allyl fragments, and is shown in the animation clearly on the right.

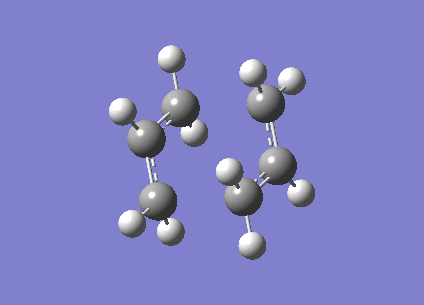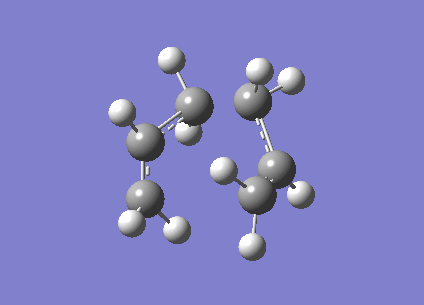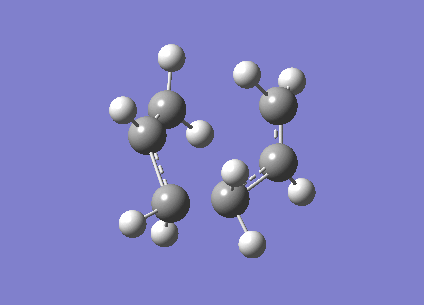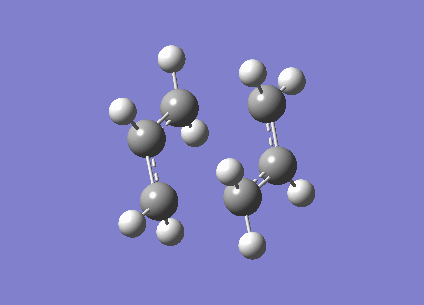
Another way of finding the transition state is the "frozen coordinate method". By taking the same guess at the chair structure and freezing the positions of the atoms at which the single bonds are formed/broken, using the Redundant Coordinate Editor, we can optimise (at the HF/3-21G level) the rest of the structure to a minimum. This structure is similar to the previously optimised chair structure, however the single bonds that are formed/broken are frozen at 2.2A apart.

Here is a link to the logfile for the optimisation of the rest of the structure File:CHAIR TS HF 3 21G OPT FROZEN P1.LOG

By opening the Redundant Coordinate Editor we can now select the "derivative" option instead of the "freeze coordinate" option, which allows GaussView to optimise the structure along the bond between these atoms. This optimised structure has the distance between the two allyl fragments at 2.02A, like the previously optimised structure, and a frequency analysis shows the same negative frequency at -818cm^-1 as well, corresponding to the same bond breaking/forming motion.

Here is a link to the logfile for the optimisation along the single bonds File:CHAIR TS HF 3 21G OPT FROZEN P2.LOG

Here is a link to the logfile for the frequency analysis File:CHAIR TS HF 3 21G FREQ FROZEN P2.LOG

Boat Transition State

Another method to optimise a transition state is to use the QST2 method, in which you specify the reactants and the products and GaussView calculates the transition state between them. The atoms of the reactant and product need to be labeled in the correct order, so as to correspond to the following diagram.

The DFT-B3LYP/6-31G* optimised anti-periplanar 2 conformation is loaded into Gaussview, and copied into a double window MolGroup as the reactant and product, with labeling like this.

An opt+freq analysis is run, with the "Optimization to a TS (QST2)" option selected. This caluclation gives a structure more like the chair transition state, with the bonds forming diagonally across the transition state instead of on either side (see right). This is because the system was not labelled correctly for the way GaussView calculated the optimisation, as during the calculation GaussView only translates the top allyl fragment and does not rotate the central bond between C3 and C4.

Here is a link to the logfile for the failed opt+freq analysis File:BOAT TS HF 3 21G OPT FREQ QST2-FAIL.LOG

Going back to the initial set up, the product and reactant structures can be modified to look more like the boat transition structure, by changing the central C2-C3-C4-C5 dihedral angle to 0^o and the C2-C3-C4 and C3-C4-C5 bond angles to 100^o, as below.

The opt+freq analysis is run again, with the "Optimization to a TS (QST2)" option selected. Now the structure resembles the boat transition state expected. The allyl fragments are separated by 2.14A, which is further than the chair transition state due to the increase in steric repulsion between the central CH's. The frequency of the vibration is at -840cm^-1, which reflects the higher energy of this vibration in comparison to the chair transition state at -818cm^-1, but the motion of the atoms is the same, as shown below (click on image to animate). This is expected as the boat transition state is meant to be higher in energy, meaning the energy of the bond forming/breaking motion should be larger.

Here is a link to the logfile for the QST2 opt+freq analysis File:BOAT TS HF 3 21G OPT FREQ QST2.LOG

The QST3 method is similar to the QST2, but there is another window in which a guess at the structure of the transition state is made. Using the transition state just found as the guess, we can now calculate the transition state from the DFT-B3LYP/6-31G* optimised anti-periplanar 2 conformation without modifying the dihedral or internal angles. After an opt+freq analysis, now with the "Optimization to a TS (QST3)" option selected, we find the separation of the allyl fragments to be 2.14A again, and the frequency and motion of the bond formation/breaking to be the same as in the QST2 case.

Here is a link to the logfile for the QST3 opt+freq analysis File:BOAT TS HF 3 21G OPT FREQ QST3.LOG

Finding the Product From the Transition State

Once the transition state has been found, we can run an intrinsic reaction coordinate calculation, which plots the minimum energy path to a minimum on the potential energy surface. It does this by altering the geometry of the molecule slightly and calculating the potential energies of the new conformations, and then moving in the direction where the gradient of the potential energy surface is steepest.

Chair Transition State

The product from the chair transition state was optimised with the IRC method, at the HF/3-21G level first. The calculation was set up so that it was computed in the forward direction only as the reaction is symmetric. The force constants were always calculated and it calculated 50 points along the IRC.

Here is a link to the logfile for the IRC analysis File:CHAIR TS HF 3 21G IRC.LOG

There are 44 intermediate geometries before the IRC calculation gives an optimised structure resembling the gauche 2 conformation of 1,5-hexadiene, as shown on the right. However it differs slightly in energy because the minimum energy has not been found properly by the IRC method. In order to find the minimum energy structure there are 3 options. Firstly, the final geometry is optimised normally, at the HF/3-21G level, secondly the IRC can be run but to calculate more points, in this case 100 and 250 were tested, or finally the IRC can be set up to compute the force constants at every step. The following diagrams show the energy at each step of the IRC and the slope at each step.

This shows a minimum in the PES is found. The gradient starts at 0 when it is at the transition state, it then increases as it moves towards the minimum energy, at which point it becomes 0 again.

Here is a link to the logfile for the optimisation of the final geometry File:CHAIR TS HF 3 21G OPT AFTER IRC.LOG

Here is a link to the logfile for the IRC analysis computing 100 steps File:CHAIR TS HF 3 21G IRC 100.LOG

Here is a link to the logfile for the IRC analysis computing 250 steps File:CHAIR TS HF 3 21G IRC 250.LOG

Here is a link to the logfile for the IRC analysis computing the force constants at every step File:CHAIR TS HF 3 21G IRC FC EVERY STEP.LOG

It was found that computing more steps, or computing the force constants at every step gave the same structure as the initial IRC optimisation, however optimising the final geometry gave the gauche 2 conformation with the exact same energy as when it was calculated at the beginning of this report; -231.69167 a.u.

Boat Transition State

The product from the boat transition state was computed in the same way, firstly in the forward direction, with the force constants always calculated and 50 steps calculated, then with 250 steps then with the force constants computed at every step.

Here is a link to the logfile for the IRC analysis computing 50 steps File:BOAT TS HF 3 21G IRC.LOG

Here is a link to the logfile for the IRC analysis computing 250 steps File:BOAT TS HF 3 21G IRC 250.LOG

Here is a link to the logfile for the IRC analysis computing the force constants at every step File:BOAT TS HF 3 21G IRC FC EVERY STEP.LOG

There are 51 intermediate geometries in the 50 step calculations, but 76 in the 250 step calculation. The structures resemble the gauche 3 conformation of 1,5-hexadiene, as shown on the right. The two 50 step calculations both have the same energy, which is greater than the energy of the 250 step calculation. They are still all higher in energy than the originally optimised structure at the start of the report however; -231.69266121 a.u. By taking the final geometry from the 250 step calculation and optimising it at the HF/3-21G level a structure with this energy is found however.

Here is a link to the logfile for the optimisation of the final geometry File:BOAT TS HF 3 21G OPT AFTER IRC.LOG

It can be seen from the following diagram that the gauche 2 conformation (above) would lead to a chair transition state, and the gauche 3 conformation (below) would lead to a boat transition state, simply be changing the dihedral angle between C2-C3-C4-C5, showing the IRC analysis predicted the correct reaction pathway.

How the products relate to the transition states.

Activation Energy for the Different Transition States

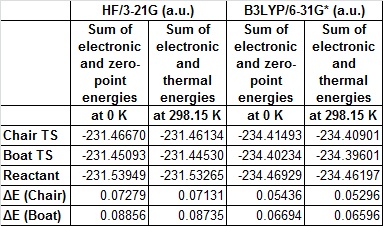
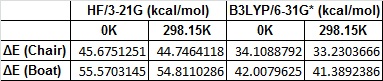
By looking at the energy of the transition states, we can calculate the activation energy of the Cope rearrangement. The boat and chair transition structures are reoptimised at the DFT--B3LYP/6-31G* level, and a frequency analysis run too to gain more information on the thermochemistry. The following table summarises the energies of each state and the activation energies. The activation energies are worked out by taking the energy of the lowest energy 1,5-hexadiene conformer (gauche 3 for the HF/3-21G level, app 1 for the DFT--B3LYP/6-31G* level) from the energy of the respective transition states.

The activation energies in kcalmol^-1 are given in the following table

The 6-31G* analysis clearly corresponds well to the literature values of 33.5 ± 0.5 kcalmol^-1 for the chair transition state and 44.7 ± 2.0 kcalmol^-1 for the boat transition state at 0 K.^[3] It is also clear that the 6-31G* level is a far more accurate method to calculate the activation energy of the rearrangement.

Here is a link to the logfile for the frequency analysis of the app 1 File:1 5 HEXADIENE APP DFT 6 31G D FREQ.LOG

Here is a link to the logfile for the frequency analysis of the gauche 3 File:1 5 HEXADIENE GAUCHE3 HF 3 21G FREQ.LOG

Here is a link to the logfile for the 3-21G opt+freq analysis of the chair File:CHAIR TS HF 3 21G OPT FREQ.LOG

Here is a link to the logfile for the 3-21G opt+freq analysis of the boat File:BOAT TS HF 3 21G OPT FREQ.LOG

Here is a link to the logfile for the 6-31G* optimisation of the chair File:CHAIR TS DFT 6 31G OPT.LOG

Here is a link to the logfile for the 6-31G* frequency analysis of the chair File:CHAIR TS DFT 6 31G FREQ.LOG

Here is a link to the logfile for the 6-31G* optimisation of the boat File:BOAT TS DFT 6 31G OPT.LOG

Here is a link to the logfile for the 6-31G* frequency analysis of the boat File:BOAT TS DFT 6 31G FREQ.LOG

Diels Alder Cycloaddition

The Diels Alder reaction is the concerted cycloaddition of a diene and a dienophile. The diene must be conjugated and in the cis conformation, and the reaction is driven by the formation of two sigma bonds, which are formed at the expense of two weaker pi bonds. The pi orbitals of the diene overlap with the pi orbitals of the dienophile, with the HOMO of one interacting with the LUMO of the other. In general, it is the HOMO of the electron rich diene that interacts with the LUMO of the electron poor dienophile; this is a "normal" Diels Alder reaction. However if the energies of the orbitals are ordered the other way around it can be an interaction between the LUMO of the diene and the dienophile HOMO; this is an "inverse" Diels Alder reaction.^[4] For a normal DA, electron withdrawing groups on the dienophile make the LUMO lower in energy, and electron donating groups on the diene make the HOMO higher in energy. This leads to a better overlap of the orbitals so a greater stabilisation energy. The opposite is true for an inverse DA. One other condition for the reaction to work is that the orbitals need to have the correct phase. The diagram below shows how the HOMOs and LUMOs of a simple diene and dienophile interact. They can either be symmetric or antisymmetric about the plane drawn, however a symmetric HOMO must interact with a symmetric LUMO, and an antisymmetric HOMO must interact with an antisymmetric LUMO. The reason for this can be seen on the right hand side of the diagram, as these lead to a positive overlap of the obitals in both cases. If a symmetric orbital were to interact with an antisymmetric orbital, the net overlap would be 0.

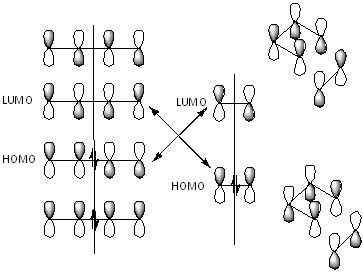
Form and symmetry of the HOMOs and LUMOs.

Reaction Between Cis-Butadiene and Ethene

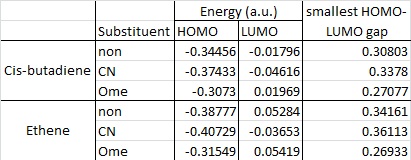
The simplest diene and dienophile combination are cis-butadiene and ethene. These are individually optimised using the semi-emperical/AM1 method, which is a simplified version of the Hartree Fock method, using some emperical values to improve the speed of the calculation.^[5] The HOMOs and LUMOs of each are shown in the table below, and their symmetries summarised. It is clear they correspond to the LCAOs of cis-butadiene and ethene in the diagram above.

	Cis-Butadiene	Ethene
HOMO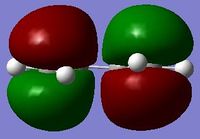
Symmetry	Anti-Symmetric	Symmetric
LUMO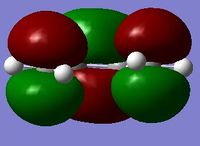
Symmetry	Symmetric	Anti-Symmetric

Here is a link to the logfile for the opt+freq analysis of cis-butadiene File:CIS BUTADIENE AM1 OPT FREQ.LOG

Here is a link to the logfile for the opt+freq analysis of ethene File:ETHENE AM1 OPT FREQ.LOG

Note it was found that if you start with a planar structure for cis-butadiene, then a tansition state is found with a negative frequency. This is because the curvature on wither side of the transition state PES is symmetric, so GaussView cannot decide which way to go, To avoid this, the dihedral angle was altered slightly from 0, and the optimisation found a minimum.

The transition state is then calculated by drawing a guess at the structure and running a opt+freq TS (Berny) analysis at the HF/3-21G level, giving the transition state geometry on the right. There is a negative frequency at -818cm^-1, showing a transition state has been found. The motion of this frequency corresponds to the formation of 2 single bonds between the cis-butadiene and ethene, in a concerted fashion as in the Diels Alder reaction. The motion is shown below (click on image to animate).

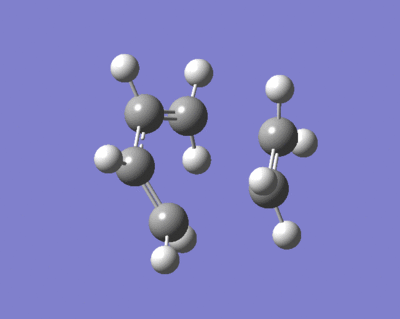
Here is a link to the logfile for the opt+freq analysis File:CYCLOHEXENE TS HF 3 21G OPT FREQ.LOG

The lowest positive frequency is at 167cm^-1 and is visualised below (click on image to animate). Unlike the negative frequency, this shows no bond stretching motions, as reflected by the smaller magnitude of the vibration. This is simply a rotation, with no bond braeaking or forming motions.

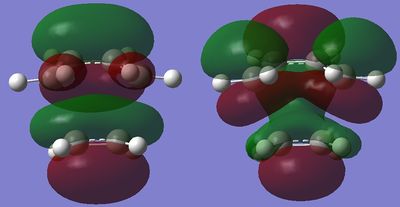
The HOMO and LUMO of the transition state are shown on the right, and it can be seen that these correspond to the interaction between the cis-butadiene LUMO and the ethene HOMO; an inverse DA. This is also reflected by the fact the TS HOMO and LUMO are symmetrical, like the cis-butadiene LUMO and ethene HOMO, showing it must be these orbitals involved in the interaction. The transition state shows 3 nodal planes in the HOMO and the LUMO.

The distance between the carbon atoms at which the bond is formed is 2.21A. Typical C-C and C=C bond lengths are 1.54A and 1.42A respectively.^[6] and the Van der Waals radius of carbon is 1.70A.^[7] The bond length in the transition state is much larger than these, so the bond has only just started to be formed, but is still only a weak interaction. The bond lengths of the double bonds of cis-butadiene got longer, to 1.37A from 1.33A, as they go from a double to a single bond, and the bond length of the single bond has decreased as it goes from a single to double bond, from 1.45A to 1.39A. The ethene bond length has increased from 1.32A to 1.37A as it goes from a double to single bond too.

Effect of Functional Groups

As stated in the introduction to the Diels Alder reaction, electron withdrawing or donating substituents on the diene or dienophile can alter the energy of the HOMO and LUMO to help the reaction. Using OMe as an electron donating group, and CN as an electron withdrawing group, the following table summarises how the energies of the HOMOs and LUMOs change with the different substituents. Calculations are run at the semi-empirical/AM1 level again now, the HF/3-21G level will be used to calculate transition states, however the AM1 level is sufficient to get an idea of the structures and their energies.

Here is a link to the logfile for the optimisation of cis-butadiene with OME File:CIS BUTADIENE OME AM1 OPT FREQ.LOG

Here is a link to the logfile for the optimisation of cis-butadiene with CN File:CIS BUTADIENE CN AM1 OPT FREQ.LOG

Here is a link to the logfile for the optimisation of ethene with OME File:ETHENE OME AM1 OPT FREQ.LOG

Here is a link to the logfile for the optimisation of ethene with CN File:ETHENE CN AM1 OPT FREQ.LOG

It can be seen that with no substituents the energy gap between the HOMO of ethene and the LUMO of cis-butadiene is smaller than the gap between the LUMO of ethene and the HOMO of cis-butadiene. Hence the reaction occurs between the cis-butadiene LUMO and the ethene HOMO. With the addition of EW and ED functional groups, the smallest gap is now when ethene has the electron donating OMe group, and cis-butadiene has the electron withdrawing CN group, as is expected for an inverse electron demand DA reation.

Reaction Between Cyclohexa-1,3-diene and Maleic Anhydride

To further investigate the effects of an electron withdrawing group on the dienophile and electron donating groups on the diene, the reaction of cyclohexa-1,3-diene and maleic anhydride is looked at. The R groups on the cyclohexa-1,3-diene are electron donating, and the (C=O)-O-(C=O) group on the maleic anhydride is extremely electron withdrawing. The HOMO and LUMO of each are shown below.

	Cyclohexadiene	Maleic Anhydride
HOMO
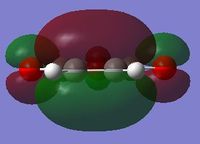
Symmetry	Anti-Symmetric	Symmetric
LUMO
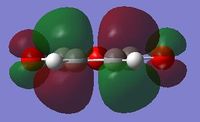
Symmetry	Symmetric	Anti-Symmetric

Here is a link to the logfile for the optimisation of cyclohexa-1,3-diene File:CYCLOHEXA 1 3 DIENE AM1 OPT FREQ.LOG

Here is a link to the logfile for the optimisation of maleic anhydride File:MALEIC ANHYDRIDE AM1 OPT FREQ.LOG

There is another characteristic of the Diels Alder revealed when looking at this reaction however, and that is that the reaction can proceed regioselectively via two transition states; exo or endo. The endo is more stabilised than the exo, due to secondary orbital interactions. This is a phenomena described as the positive interaction between the non bond forming pi orbitals of the diene with the non bond forming pi orbitals on the dienophile.^[8]

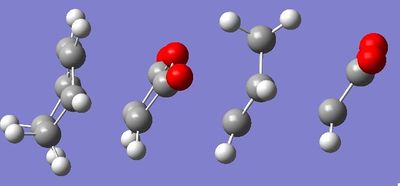
The endo and exo transition states are found, as on the right, via the TS Berny method again, now at the HF/3-21G level of theory. They both have a negative frequency, showing a transition state has been found. The exo TS is at -647cm^-1, and the endo at -644cm^-1. The endo is a lower, so is an easier motion energetically. The motions are shown below (click on image to animate), and correspond to the synchronous bond breaking/forming motions of the respective Diels Alder cycloadditions.

Here is a link to the logfile for the opt+freq analysis for the exo TS File:EXO TS HF 3 21G OPT FREQ.LOG

Here is a link to the logfile for the opt+freq analysis for the endo TS File:ENDO TS HF 3 21G OPT FREQ.LOG

The distance between the carbon atoms at which the bond is formed is 2.23A for the endo TS, and 2.26A for the exo. Again these are greater than the Van der Waals radius, so a bond is not properly formed. The bond lengths of the double bonds of cyclohexa-1,3-diene got longer, from 1.34A to 1.37A in the endo and exo, as they go from a double to a single bond. The bond length of the single bond has decreased as it goes from a single to double bond, from 1.45A to 1.40A in the endo and exo. The maleic anhydride bond length has increased from 1.35A to 1.37A in the endo and exo, as it goes from a double to single bond too. The exo form has the bulky (C=O)-O-(C=O) group clashing with the CH₂-CH₂ group on the diene, whereas in the endo it is the small CH=CH group that clashes with the CH₂-CH₂ group, so the exo is more strained.

The distance between the π systems of the CH=CH on the cyclohexa-1,3-diene and the (C=O)-O-(C=O) on the maleic anhydride is 4.45A in the exo, and 3.10 in the endo. This suggests that the secondary orbital interactions could take place in the endo, but not the exo as the π systems are too far apart. The HOMOs and LUMOs of the transition states are shown below, and their energies are given at the reoptimised DFT-B3YLP/6-31G* level.

	Endo Transition State	Exo Transition State
HOMO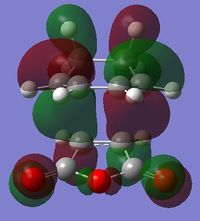
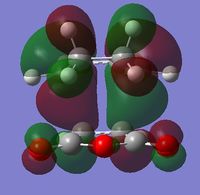
Symmetry	Anti-Symmetric	Symmetric
LUMO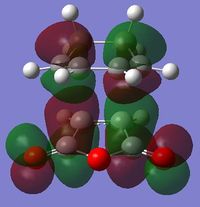
Symmetry	Symmetric	Anti-Symmetric
Energy (a.u.)	-612.68340	-612.67931

Here is a link to the logfile for the reoptimisation for the exo TS File:EXO TS DFT 6 31G OPT.LOG

Here is a link to the logfile for the reoptimisation for the endo TS File:ENDO TS DFT 6 31G OPT.LOG

As expected the energy of the exo is higher than the energy of the endo TS, with the energy difference equal to 2.57 kcalmol^-1. Looking at the HOMOs and LUMOs, there are 4 nodal planes in the HOMOs and the LUMOs (excluding the oxygen orbitals for all). It can be seen that they are both antisymmetric, so are now a normal DA interaction between the HOMO of the cyclohexa-1,3-diene and the LUMO of the maleic anhydride. This is enforced as the HOMO look like the LCAO of the diene HOMO and dienophile LUMO.

However looking at the interaction between the CH=CH and the (C=O)-O-(C=O) π systems, it can be seen there is a node between them on the exo, but also on the endo TS, suggesting there is no secondary orbital interaction. J. I Garcia et al^[9] suggest that the so called secondary orbital effects are in fact non existant, and the difference in energy can be explained by far more common interactions, such as steric interactions, hydrogen bonds, solvent effects, electrostatic forces etc., as do M. A. Fox et al.^[10]

References

↑ P. Echenique, J. L. Alonso, Molecular Physics, 105, 3057-3098, 2007 DOI:10.1080/00268970701757875
↑ J. L. Durrant, Chemical Physics Letters, 256, 595–602, 1996 DOI:10.1016/0009-2614(96)00478-2
↑ M. M. Khaledy, M. Y. S. Kalani, K. S. Khuong and K. N. Houk, J. Org. Chem. 68, 572-577 , 2003 DOI:10.1021/jo020595b
↑ J. Sauer and R. Sustmann, Angew. C'hem., 19, 779-807, 1980 DOI:10.1002/anie.198007791
↑ M. J. S, Dewar, E. G. Zoebisch, E. F. Healy, J. J. P. Stewart, Journal of the American Chemical Society 107 (13), 3902–3909, 1985 DOI:10.1021/ja00299a024
↑ W. Qin, Y. Wang, Y. Huang, Z. Zhou, C. Yang and Chang Q. Sun, The Journal of Physical Chemistry A 116 (30), 7892-7897, 2012 DOI:10.1021/jp905336j
↑ A. Bondi, . Phys. Chem., 68 (3), 441–451, 1964 DOI:10.1021/j100785a001
↑ M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 52 (8), 1469–1474, 1987 DOI:10.1021/jo00384a016
↑ J. I. García, J A. Mayoral and L. Salvatella, Acc. Chem. Res., 33, 658-664, 2000 DOI:10.1021/ar0000152
↑ M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 52 (8), 1469–1474, 1987 DOI:10.1021/jo00384a016

[1] P. Echenique, J. L. Alonso, Molecular Physics, 105, 3057-3098, 2007 DOI:10.1080/00268970701757875

[2] J. L. Durrant, Chemical Physics Letters, 256, 595–602, 1996 DOI:10.1016/0009-2614(96)00478-2

[3] M. M. Khaledy, M. Y. S. Kalani, K. S. Khuong and K. N. Houk, J. Org. Chem. 68, 572-577 , 2003 DOI:10.1021/jo020595b

[4] J. Sauer and R. Sustmann, Angew. C'hem., 19, 779-807, 1980 DOI:10.1002/anie.198007791

[5] M. J. S, Dewar, E. G. Zoebisch, E. F. Healy, J. J. P. Stewart, Journal of the American Chemical Society 107 (13), 3902–3909, 1985 DOI:10.1021/ja00299a024

[6] W. Qin, Y. Wang, Y. Huang, Z. Zhou, C. Yang and Chang Q. Sun, The Journal of Physical Chemistry A 116 (30), 7892-7897, 2012 DOI:10.1021/jp905336j

[7] A. Bondi, . Phys. Chem., 68 (3), 441–451, 1964 DOI:10.1021/j100785a001

[8] M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 52 (8), 1469–1474, 1987 DOI:10.1021/jo00384a016

[9] J. I. García, J A. Mayoral and L. Salvatella, Acc. Chem. Res., 33, 658-664, 2000 DOI:10.1021/ar0000152

[10] M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 52 (8), 1469–1474, 1987 DOI:10.1021/jo00384a016

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]