Rep:Mod:jjbpage
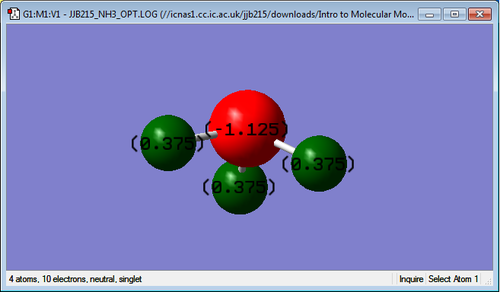
NH3 molecule
General information
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -56.55776873 au |
| RMS gradient | 0.00000485 au |
| Point group | C3v |
| N-H bond distance | 1.01798Å |
| H-N-H bond angle | 105.741° |
Item table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986279D-10
Optimization completed.
-- Stationary point found.
The log file of the optimised structure is linked here
3D structure
NH3 Molecule |
Vibrational information
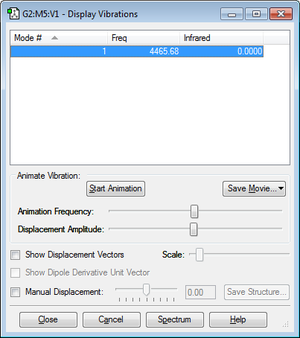
Active vibrations of optimised NH3 molecule at 0 Kelvin show that none of the frequencies are negative; hence, the molecule is fully optimised.
The expected number of modes from the 3N-6 rule is 6 because there are 4 atoms (N=4). Modes 2 & 3 and modes 5 & 6 are degenerate because they have the same frequency. Modes 1, 2 and 3 are bending vibrations, whilst modes 4, 5 and 6 are bond stretching vibrations. The mode that is highly symmetric is 4. The 'umbrella' mode is 1. The expected number of bands in an experimental IR spectrum of gaseous ammonia is 4, because there are 2 pairs of modes that are degenerate; therefore, the degenerate pairs will only have one distinct band. However, because the intensities of modes 4, 5 and 6 are too low due to a small change in dipole moment, only 2 bands are clearly seen in a spectrum.
Charge information
Charge of N atom: -1.125C
Charge of H atoms: +0.375C
The expected charge on the N atom is negative and on the H atoms are positive because N is more electronegative than H. Therefore, there is more electron density closer to the N atom compared to the H atoms.
N2 molecule
General information
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -109.52412868 au |
| RMS gradient | 0.00000060 au |
| Point group | D∞h |
| N-N bond distance | 1.10550Å |
Item table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400980D-13
Optimization completed.
-- Stationary point found.
The log file of the optimised structure is linked here
3D structure
N2 Molecule |
Vibrational information
Active vibrations of optimised N2 molecule at 0 Kelvin show that none of the frequencies are negative; hence, the molecule is fully optimised.
The 3N-5 rule is used because N2 is a linear molecule and from this rule, the expected number of modes is 1 because there are 2 atoms (N=2). This single mode is a bond stretching vibration.
H2 molecule
General information
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -1.17853936 au |
| RMS gradient | 0.00000017 au |
| Point group | D∞h |
| H-H bond distance | 0.74279Å |
Item table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
The log file of the optimised structure is linked here
3D structure
H2 Molecule |
Vibrational information
Active vibrations of optimised H2 molecule at 0 Kelvin show that none of the frequencies are negative; hence, the molecule is fully optimised.
The 3N-5 rule is used because H2 is a linear molecule and from this rule, the expected number of modes is 1 because there are 2 atoms (N=2). This single mode is a bond stretching vibration.
Haber-Bosch reaction
Reaction
N2 + 3H2 ---> 2NH3
Energy calculation
E(NH3)= -56.55776873 au
2*E(NH3)= -113.11553746 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 au or -146.47848285 kJ/mol
ΔE= -146.48 kJ/mol (2dp)
The ammonia product is more stable because ΔE is negative, meaning an exothermic reaction and the energy of the ammonia product is lower than the energy of the starting reactants (H2 and N2)
Project molecule: ClF
General information
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -559.94269578 au |
| RMS gradient | 0.00014211 au |
| Point group | C∞v |
| Cl-F bond distance | 1.66434Å |
Item table
Item Value Threshold Converged?
Maximum Force 0.000246 0.000450 YES
RMS Force 0.000246 0.000300 YES
Maximum Displacement 0.000433 0.001800 YES
RMS Displacement 0.000613 0.001200 YES
Predicted change in Energy=-1.066055D-07
Optimization completed.
-- Stationary point found.
The log file of the optimised structure is linked here
3D structure
ClF Molecule |
Vibrational information
Active vibrations of optimised ClF molecule at 0 Kelvin show that none of the frequencies are negative; hence, the molecule is fully optimised.
The 3N-5 rule is used because ClF is a linear molecule and from this rule, the expected number of modes is 1 because there are 2 atoms (N=2). This single mode is a bond stretching vibration.
Charge information
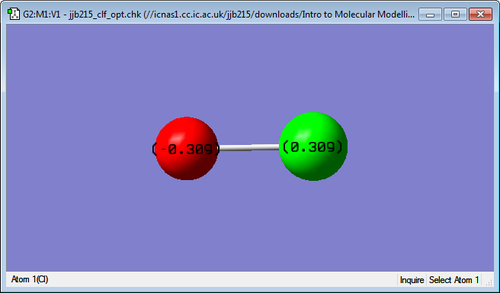
Charge of F atom: -0.309C
Charge of Cl atom: +0.309C
The expected charge on the F atom is negative and on the Cl atom is positive because F is more electronegative than Cl. Therefore, there is more electron density drawn closer to the F atom compared to the Cl atom.
Molecular orbitals information
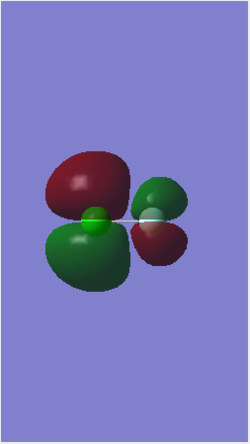
MO 7 is an occupied molecular orbital (MO) formed from the in-phase overlap of the 3s atomic orbital (AO) of Cl and the 2s AO of F. This overlap forms a bonding σ orbital with an energy of -1.21864 au, this energy is relatively high because it is formed from valence AOs. Also, the AO of F contributes more to the bonding character of the MO because F is more electronegative and this means that the 2s AO of F is closer in energy to the resulting MO7. The anti-bonding pair of this MO is MO 8.
MO 8 is an occupied MO formed from the anti-phase overlap of the 3s AO of Cl and the 2s AO of F. This overlap forms an anti-bonding σ* orbital with an energy of -0.83311 au, which is higher than MO 7 because it’s an anti-bonding orbital. The anti-bonding character of the MO gains more contribution from the AO of Cl because it's less electronegative than F and this means that its 3s AO is closer in energy to the resulting anti-bonding MO in comparison to the 2s AO of F. This MO is in a pair with MO 7, which is a bonding MO.
MO 9 is an occupied MO formed from the in-phase, end-on overlap of the 3pz AO of Cl and the 2pz AO of F. This overlap forms another bonding σ orbital with an energy of -0.52314 au. The energy is higher than MO 7 & 8 because p orbitals have a higher energy than s orbitals. The 2pz AO of F contributes more bonding character to the resulting bonding orbital because F is very electronegative and therefore, its AO is closer in energy to MO 9. The anti-bonding pair of this MO is MO 14.
MO 12 & 13 are degenerate MOs because they have the same energy of -0.32855 au. The only difference between the MOs is the orientation, where MO 12 is formed from the overlap of 3px of Cl and 2px of F and MO 13 is formed from the overlap of 3py of Cl and 2py of F. Both MOs are formed from the anti-phase, side-on overlap of p orbitals to form anti-bonding π* orbitals. These orbitals are called the highest occupied molecular orbitals (HOMOs) because they are occupied orbitals highest in energy. These anti-bonding MOs also gain more anti-bonding character from the 3p AOs of Cl because it is less electronegative than F, meaning that the 3p AOs of CL are much higher in energy and closer in energy to the anti-bonding MO 12 & 13.
MO 14 is an unoccupied MO formed from the anti-phase, end-on overlap of the 3pz AO of Cl and the 2pz AO of F. This overlap forms an anti-bonding σ* orbital with an energy of -0.12150 au. The fact that this MO is an unoccupied orbital with the lowest energy means that it is the lowest unoccupied molecular orbital (LUMO). This anti-bonding MO gains more anti-bonding character from the 3pz AO of Cl because Cl is less electronegative than F and this means that the 3pz AO of Cl is higher in energy and closer to the energy of the resulting MO 14. This MO is in a pair with MO 9, which is the bonding MO.
ClF3 molecule
General information
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) | -759.46531674 au |
| RMS gradient | 0.00009315 au |
| Point group | CS |
| Cl-F bond distance (axial F) | 1.72881Å |
| Cl-F bond distance (equatorial F) | 1.65163Å |
| F-Cl-F bond angle (axial F atoms) | 174.238° |
| F-Cl-F bond angle (axial and equatorial F) | 87.119° |
The Cl-F bond distances are different because the axial F atoms are repelled more because they are much closer to the 2 lone pairs of the molecule. In comparison to the ClF molecule, ClF3 has a trigonal bipyramidal pseudo structure because there are 5 areas of electron density around the central Cl atom. The structure is T-shaped because of the 2 lone pairs.
Item table
Item Value Threshold Converged?
Maximum Force 0.000132 0.000450 YES
RMS Force 0.000093 0.000300 YES
Maximum Displacement 0.000733 0.001800 YES
RMS Displacement 0.000455 0.001200 YES
Predicted change in Energy=-1.543574D-07
Optimization completed.
-- Stationary point found.
The log file of the optimised structure is linked here
3D structure
ClF3 Molecule |
Vibrational information
Active vibrations of optimised ClF3 molecule at 0 Kelvin show that none of the frequencies are negative; hence, the molecule is fully optimised.
From the 3N-6 rule(because the molecule is non-linear), the expected number of modes is 6 because there are 4 atoms (N=4).
Charge information
Charge of axial F atoms: -0.454C
Charge of equatorial F atom: -0.316C
Charge of Cl atom: +1.224C
The expected charges on the F atoms are negative and on the Cl atom is positive because F is more electronegative than Cl. Therefore, there is more electron density drawn closer to the F atom compared to the Cl atom. The charges of the axial F atoms are more negative than the equatorial F atom because the 2 lone pairs of the molecule are much closer to the axial F atoms, this means that they attract more electron density compared to the F atom in the equatorial position.