Rep:Mod:jialeiq4111c

Conformation Analysis using Molecular Mechanics

Dimerisation of Cyclopentadiene

The dimerization of cyclopentadiene is a _π4_s + _π2_s cycloaddition reaction. Under thermal reaction condition, it proceeds with zero antarafacial component via a 6-membered cyclic transition state with Huckel aromaticity. The selection rule for such pericyclic reaction stems from the conservation of orbital symmetry during a thermal or photochemical pericyclic reaction.

For the dimerization of cyclopentadiene, the frontier orbitals to be considered are i) bonding HOMO ψ2 of one molecule and ii) anti-bonding LUMO ψ3 of the other. As discussed, the reaction proceeds with zero antarafacial component. Therefore, there are two possible ways in which the orbitals could combine through only sufrafacial component. As illustrated in Fig. 1, the two new σ bonds can either form on the bottom face of both molecules to give the endo isomer 2, or form on the bottom face of one molecule to the top face of the other to give the exo isomer 1.

Figure 1: Diagram showing orbital interaction leading to exo and endo products from dimerisation of cyclopentadiene

Molecular mechanics calculation was performed to better understand the relative stabilities of the two isomers. Both isomer 1 and 2 were created using ChemDraw Pro 13.0 and then optimised using Avogadro 5.0 with MMFF94s force field and conjugated gradient. The lowest energy conformation of the isomers were obtained when an energy minima was reached for which dE = 0. The calculated energies and optimised structures are summarised in Table 1.

Table 1: Summarised Result from Optimization of Dicyclopentadiene Isomers

Isomer	1 (exo)	2 (endo)
Optimised Structure	Isomer 1	Isomer 2
Total Energy/ kcal mol-1	55.37344	58.19070
Total Bond Stretching Energy/ kcal mol-1	3.54306	3.46743
Total Angle Bending Energy / kcal mol-1	30.77272	33.19138
Total Torsional Energy/ kcal mol-1	-2.7311	-2.08211
Total Van der Waals Energy/ kcal mol-1	12.80159	12.35719
Total Electrostatic Energy/ kcal mol-1	13.01372	14.18428

By comparing the total energy of the two isomers, it was noted that isomer 1 is thermodynamically more stable than isomer 2 by ~2.8 kcal/mol. Both molecules have very large and positive angle bending energies which suggests considerable angle strain in the molecules. This is due to the bridged-bicyclic structure in which neither ideal C-C-C bond angle about sp³ nor sp² carbon centre could be achieved. The difference in angle bending energies between the isomers is the greatest compared to differences in other components. Since isomer 1 has a less positive angle bending energy than 2, we can deduce that the differential stabilities of the isomers is likely to be due mainly to difference in angle strain. From examination of the bond angle in the carbon framework, it was noticed that there is a greater deviation from ideal bond angle about the carbons of the newly formed σ bond in isomer 2 than 1 as illustrated in Fig. 2. In addition, the two cyclopentene rings are on the same side in 2 which results in greater steric repulsion.

Figure 2: Diagram showing key bond angles and H---H distance in isomer 1 and 2

Both bond stretch energies and torsion energies are comparatively small contributions and there are little differences. Examining the relative Van der Waals energy, it was observed that Van der Waals interaction is less unfavourable in isomer 2 than 1. The highlighted H---H Van der Waals interactions in Fig. 2 shows the most significant discrepancy across the molecule. The slightly shorter H---H distance in isomer 2 could confer it slight greater magnitude of attractive Van der Waals interaction.

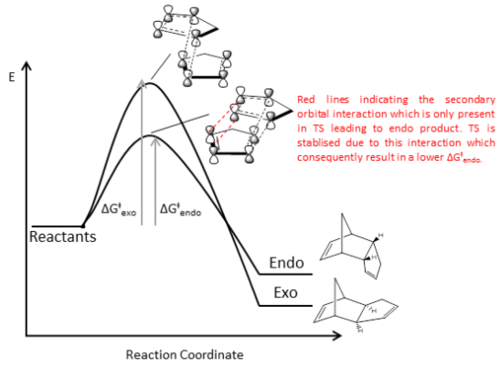
Overall, molecular mechanics calculation shows that isomer 1 is more thermodynamically stable than 2. Therefore, under reversible reaction condition and thermodynamic control, the more thermodynamically stable exo product 1 will be the major product. However, in this case, endo product 2 is formed specifically under mild condition . This indicates that the reaction operates irreversibly and is under kinetic control in which the fastest forming product is the major product of reaction. Therefore, we could infer that the transition state leading to the formation of 2 is more stable than 1 which would have a smaller activation energy barrier and consequently a much faster rate of formation. The stabilisation of the transition state leading to 2 can be attributed to secondary orbital interactions between the p orbitals which are not directly involved in σ bond formation as shown in Fig. 3. This secondary orbital interaction was proposed to lead to the donation of mobile electron density from the bonding π orbital to the anti-bonding π* orbital during transition state to achieve stabilization through electrostatic and electrodynamic attractions. In contrast, due to the selection rule of pericyclic reaction, this interaction is not possible to achieve in the transition state of 1.

Figure 3: Energy profile diagram of dimerisation reaction of cyclopentadiene

Hydrogenation of Diyclopentadiene

The hydrogenation of endo-dicyclopentadiene (DCPD) to dihydrodicyclopentadiene (DHDCPD) and further to tetrahydrodicyclopentadiene (THDCPD) has important industrial importance in the energy and materials sector . It has been reported that initial hydrogenation of DCPD leads predominantly to 9,10-DHDCPD 4 rather than 1,2-DHDCPD 3. In this section, both hydrogenated products 3 and 4 has been optimised using molecular mechanics method with Avogadro and MMFF94s force field in an attempt to rationalise the regioselectivity of this hydrogenation reaction. The calculated energies and optimised structures are summarised in Table 2.

Table 2: Summarised Result from Optimization of DHDCPD Isomers

Isomer	1,2-DHDCPD (3)	9,10-DHDCPD (4)
Optimised Structure	molecule 3	molecule 4
Total Energy/ kcal mol-1	50.44570	41.25749
Total Bond Stretching Energy/ kcal mol-1	3.31112	2.82314
Total Angle Bending Energy / kcal mol-1	31.93573	24.68527
Total Torsional Energy/ kcal mol-1	-1.47033	-0.37851
Total Van der Waals Energy/ kcal mol-1	13.63861	10.63749
Total Electrostatic Energy/ kcal mol-1	5.11950	5.14702

The total energy of 4 is lower than that of 3 by ~10 kcal/mol from molecular mechanics calculation which indicates greater relative thermodynamic stability of 4. In this case, a very large angle bending contribution is also observed and the difference in angle bending energy between the two isomers is the most significant in comparison to other energy terms. This again suggests considerable angle strain in the molecules. The large difference could mainly be attributed to the degree of deviation from ideal sp² C=C-C bond angle. As the double bond in 3 is part of a norbordene structure, it is less well accommodated in a 6-membered ring structure than the ‘’cyclopentene’’ double bond in 4. Therefore, the C=C-C bond angle of 107^o for 3 deviates more from the ideal 120^o angle than 4 as shown in Fig. 4a.

Figure 4: a) Diagram showing key bond angles about sp² C center and gauche interactions about the newly formed sp³ c; b) diagram indicating the shortening of non-bonding C-C distance in isomer 3 which could contribute towards greater Van der Waals repusive interaction.

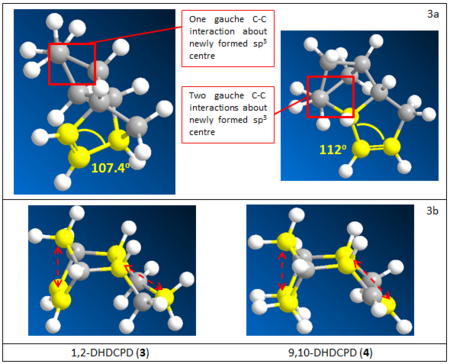
From the calculated results, another major contribution which lead to different thermodynamic stabilities of the two isomers is the Van der Waals interaction. For both molecules the Van der Waals term is large, relative to kT, and positive which indicates unfavourable Van der Waals interaction between non-bonding atoms. In isomer 3, upon hydrogenation, the cyclopentane ring adopts an envelope conformation which brings the highlighted non-bonding carbons much closer than in 4, as shown in Fig. 4b. This could have contributed towards greater repulsive Van der Waals interaction in 3. On the other hand, most of the non-bonding H—H interactions are within attractive distance for both molecules.

There is relatively small deviation of bond lengths in both molecules given by the small positive contribution of the bond stretching term. Since the difference in this energy term is very small, there’s no significant contribution towards the stabilities of the isomers. The torsional energy is also relatively small contribution. That of 3 is slightly more favourable than 4 as given by the more negative energy term. This is likely due to less eclipsed C-H bonds and gausche C-C interactions in 3, as shown in Fig. 4a, contributing to less torsion strain.

Figure 5: Diagram indicating the proposed structural rearrangement during hydrogenation reaction of endo-DCPD.

As mentioned, it has been reported that 4 is the major product of hydrogenation of endo-DCPD. The calculated result showed 4 to be the more thermodynamically stable isomer, therefore, this lead us to conclude that the reaction is under thermodynamic control. The stability of 4 is also supported by reported computational result that the HOMO-LUMO gap is smaller for 4 than 3. Upon further examination, it might be proposed that 4 is both the thermodynamic and kinetic product in this reaction. First, there is less structural reorganisation upon hydrogenation of 2 to 4 as shown in Fig. 5. It could then be inferred that less structural distortion is required to reach TS to form 4 and consequently a lower activation energy barrier. Second, norbordene C=C has longer bond length of 1.342 pm compared to 1.338 pm of the cyclopentene C=C. This shows that the norbordene C=C is slightly weaker, therefore, more easily hydrogenated as suggested by previous study. This again suggest a lower activation energy in forming 4. However, it was noted that hydrogenation of the norbordene C=C suffers slightly more steric hindrance due to the bridging C-C-C unit. Hence, overall, formation of 4 might involve a slightly lower activation energy. Despite the discussion, it has to be noted that the reaction condition is also crucial in determining whether the reaction is under thermodynamic or kinetic control. As most hydrogenation process take place under high temperature, and the kinetic biasness is likely small, it can be said that the reaction is almost always under thermodynamic control to form 4 as the major thermodynamic product.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Compound 9 and 10 are atropisomers, stereoisomers that can be isolated due to restricted rotation about a single bond, and are key intermediate in the total synthesis of widely used ovarian cancer treatment Taxol. The compound can be formed via reported antropselective oxyanionic Cope rearrangement reaction to give 9 selectively under kinetic condition. The two isomeric forms differ in the orientation of ketone functionality. Hence, isomerism is possible at high temperature and has been reported in analogous compound to offer the more thermodynamically stable isomer.. Here, molecular mechanics method used before was again employed to calculate the relative energies of the atropisomers to determine which one is the more thermodynamically stable form. Same as before, the calculation was performed using Avogadro, MMFF94s force field and conjugated gradient. The calculated energies and optimised structures are summarised in Table 3.

Table 3: Summarised Result from Optimization of Atropisomers

Isomer	9	10
Optimised Structure	Isomer 1	Isomer 2
Total Energy/ kcal mol-1	70.54149	60.55413
Total Bond Stretching Energy/ kcal mol-1	7.66504	7.60841
Total Angle Bending Energy / kcal mol-1	28.26887	18.81601
Total Torsional Energy/ kcal mol-1	0.27897	0.25966
Total Van der Waals Energy/ kcal mol-1	33.13645	33.21970
Total Electrostatic Energy/ kcal mol-1	0.30168	-0.05138

From the result, it is immediately apparent that isomer 10, with ketone pointing down with respect to the bridging unit, is more stable form by 10 kcal/mol. To understand the difference in stability, we first looking at the angle strain as there is ~10 kcal/mol energy difference in the angle bending energy term indicating its large contribution. As indicated on Table 4, the greatest difference in sp³ C-C-C bond angle are exhibited about C α to C=O. Due to medium ring size, deviation from ideal sp³ C-C-C bond angle is expected. However, the deviation is much greater for 9 than 10 by 5^o. As seen in the example of 3 than 4, 5^o degrees of difference contributed ~8 kcal/mol difference in angle bending energy. Therefore, the main discrepancy in angle bending term between 9 and 10 could be mainly accounted by these two angles.

Table 4: Table comparing structural differences between 9 and 10 which was suspected to contribute towards different thermodynamic stability of the isomers

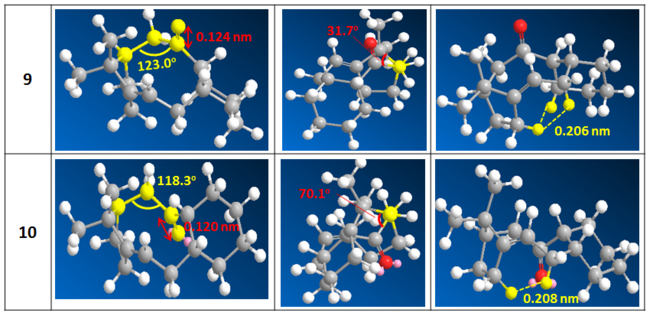
Although there is little difference in all other energy terms, upon close examination of the optimised structure, some localised differences in bond length, torsion and Van der Waals interaction was observed. First, we note that the C=O bond length differs with 0.124 nm and 0.120 nm for 9 and 10 respectively. Therefore, the C=O bond order is greater for 10. As πC=O is expected to constitute the frontier orbital, then 10 have a lower energy HOMO and consequently more stable. Referring to Table 4, the dihedral angle between C=O and the bridging unit is very compressed in 9 with torsional angle of 31^o. Whereas for 10, there is a closer and more evenly distributed gauche conformation with torsional angle of ~60^o throughout. This difference could contribute to significant torsional strain and steric repulsion in 9. Non-bonding Van der Waals interaction was also examined. The cyclohexane ring could only be placed in axial position at α’-C to achieve stable chair conformation in 9 therefore would lead one to expect greater repulsive Van der Waals interaction between the two ends of the molecule. Furthermore, there are two sets of repulsive Van der Waals H--H interaction in 9 while only one in 10. In conclusion, although other contributions might not be determining overall, there are significant localised differences in interactions which needs to be taken into account. Therefore, looking at the energy alone is sometimes insufficient and close examination of the molecule is required to gain a better picture.

This intermediate to taxol contains a cis- bridgehead olefin. Generally, bridgehead olefin is considered unstable and the formation of bridgehead olefin is unfavourable accoding to Bredt’s Rule. This is generally associated with the increased strain induced by bridgehead sp² carbon compared to sp³ carbon. Yet several compounds containing bridgehead olefin demonstrating hyperstability have been identified, including the compound under investigation.

Semi-empirical molecular mechanics methods have long been employed to predict the stability of bridgehead olefin. For the intermediate under investigation, the energy of the hydrogenation product of 10 is 71.44 kcal/mol, 10 kcal/mol greater than 10. This suggest that it is more favourable to have a sp² carbon at the bridge head position than sp³ carbon. Looking at the different contribution towards strain, the torsion and angle bending terms are both ~8 kcal/mol more unfavourable in the hydrogenated product. Although energy calculated using molecular mechanics could only be used to more accurately predict the difference between isomers, this could serve as a good estimate. Structural analysis shows that, by substituting the bridgehead carbon to sp³ C, the bond angle of 121^o is highly unfavourable. Cross-referring to literature, it has been reported that the presence of bridgehead double bond in related taxane compounds gives the compounds a flatter structure which suffers less strain than when the bridgehead position is saturated. In addition, the increase in angular strain in having bridgehead olefin is less significant compared to the increase in transannular interaction in having sp³ carbon. This is even more pronounced when the ring is substituted therefore further favouring bridgehead olefin.

Spectroscopic Simulation using Quantum Mechanics

Compound 17 has been prepared by atropselective oxy-Cope rearrangement reaction and has shown to isomerise into 18 upon heating and their spectroscopic properties has been reported. In this section, computational method is used to simulate the NMR spectrum of isomer 18 in the hope to better understand and assign the ¹H and ¹³C NMR spectrum. The molecule is constructed in ChemDaw Pro 13.0 and initially optimised using molecular mechanics method with Avogadro employing MMFF94s force field and conjugated gradient. The result of pre-optimisation has been summarised in Table 5.

Table 5: Summarised Result from pre-Optimization of 18

Isomer	18
Optimised Structure	Isomer 1
Total Energy/ kcal mol-1	100.52197
Total Bond Stretching Energy/ kcal mol-1	15.04380
Total Angle Bending Energy / kcal mol-1	30.07042
Total Torsional Energy/ kcal mol-1	9.72723
Total Van der Waals Energy/ kcal mol-1	49.56105
Total Electrostatic Energy/ kcal mol-1	-6.07576

There has been reported energy of 65.7 kcal/mol calculated using MMX force field. Yet, this value cannot be compared with the energy of 100.52 kcal/mol obtained in this experiment as a different force field was evoked. In addition to MMFF94s, MM2 calculation was also attempted on the optimised structure using ChemBio 3D 13.0 which gave 64.37 kcal/mol. There no significant conformational rearrangement of the molecule upon MM2 optimisation. Therefore, it was shown that the value obtained is highly dependent on method used. For the purpose of consistency, MMFF94s is employed throughout. The pre-optimised structure is then subjected to ab initio quantum mechanical calculation for further QM optimisation and NMR simulation. Method used for NMR simulation and summarised results are shown below.

Table 6: Summarised Results for QM NMR analysis of 18

Categories	18i	18ii	18iii
Structure	Isomer 1	Isomer 1	Isomer 1
File Type	.log
Calculation Type	FREQ
Solvent	Benzene
Calculation Method	RB3LYP
Basis Set	6-31G(D,P)
Spin	Singlet
Total Energy	-1651.88236481 a.u.	-1651.88339400 a.u.	-1651.87832240 a.u.
RMS Gradient Norm	0.00000704 a.u.	0.00000606 a.u.	0.00000791 a.u.
Dipole Moment	1.65 Debye	1.83 Debye	1.92 Debye
Job CPU time	17.0 seconds	7.0 seconds	6.0 seconds
FCHK File	File:18 nmr jq411 benzene.log	File:18 nmr jq411 v2.log	File:18 nmr jq411 twist.log
DOI	DOI:10042/28239	DOI:10042/28237	DOI:10042/28238

It should be noted that NMR spectroscopy is a dynamic technique for which the spectrum obtained is of the average signal within the time frame of the NMR experiment. Although it is difficult to compute all accessible conformation of 18 at room temperature within the allocated time, three possible conformations has been considered here. Conformations i and ii are equivalent which only differ in the conformation of puckered dithial ring. Conformation iii is a local minimum as it has a more energetically expensive twist boat structure in the cyclohexane unit. Ring flipping of these two rings was assumed to be feasible at room temperature and within the time frame of the NMR experiment. By considering these different static structures, we hope to obtain a closer approximation to the dynamic experimental situation. Both the ¹H and ¹³C NMR spectrum of the three conformation are shown, peaks are tabulated, averaged and compared to reported experimental value for further assignment and discussion.

Figure 6:Picture showing numbering of the atoms used below

Calculated ¹H and ¹³C NMR Spectrum for 3 Conformations of 18

Molecule	1H Spectrum	13C Spectrum
18i
18ii
18iii

¹³C Spectrum

Table 7: Table summarizing calculated 13C NMR chemical shift values and peak assignment against literature value. All calculated peaks are referenced to TMS and benzene was used as solvent for calculation as reported values were in benzene.

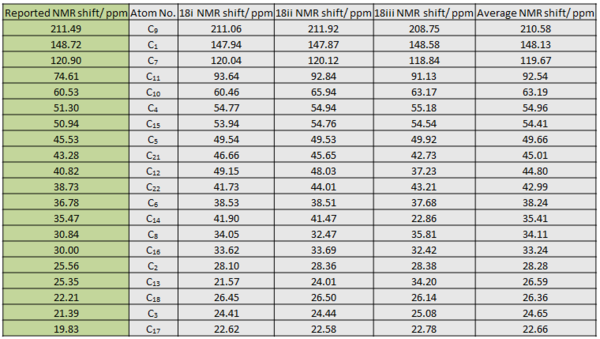
The experimental peaks and computed peaks for all three conformations have been tabulated and reference to TMS. Overall, there is little difference in the order and chemical shift values between the computed peaks for 18i and 18ii. This is expected as they only differ in relative orientation of the puckered dithial ring. 18iii has shown difference from the two in terms of chemical shift values for the clyclohexane ring carbons. This is also expected as it has a twist boat conformation in the cyclohexane ring while the other two has boat conformation. This conformation difference could lead to slight change in the chemical environment of the ring carbons especially when the chemical shifts are already very similar. As mentioned that experimental NMR is a dynamic process, the chemical shift for each C is averaged to obtain the final calculated estimate. The experimental peaks are then assigned based on comparison to this final averaged value as shown in the table above.

The final calculated estimate chemical shift is largely in good agreement with the corresponding reported value with an overall error of +2 ppm. This error is expected as not all the possible accessible conformations have been taken into account. No conclusion can be drawn as to which conformation gives the best estimate since each calculation only gives a static picture. However, when the twist boat and chair gives very different values, the averaged value is usually the closest to the experimental counter-part, take for example C₁₃ and C₁₄ of the cyclohexane ring. The greatest deviation from experimental value is the dithial carbon C₁₁. The calculated values all pointed to ~90 ppm while the experimental value is only at 74 ppm with 16 ppm difference. This overestimation is likely to be associated with the attachment to two relatively heavy S atom. A better basis set might be required for higher level calculation to get more accurate value for this carbon.

In terms of the assignment, the chemical shifts of the alkyl carbons are mainly determined by their relative proximity to electronegative atoms. The carbonyl carbon was correctly predicted at ~210 ppm due to electron withdrawing effect of the funcationality. The alkene carbons are similarly deshielded to give values between 120 – 150 ppm due to induced ring current by the π electron cloud. As mentioned, the dithial carbon did not give a good estimation but it did take into account the induction effect of the two S atoms. Overall, calculation at the given level gave a very good estimate to the experimental value.

¹H Spectrum

Table 8: Table summarizing calculated 1H NMR chemical shift values. All calculated peaks are referenced to TMS and benzene was used as solvent for calculation as reported values were in benzene.

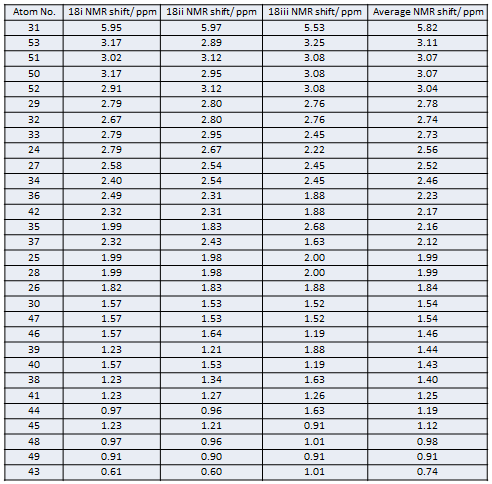
The ¹H NMR Spectrum is much more complicated that the ¹³C Spectrum simple due to the large number of methylene H. Furthermore, there has not been good literature assignment. The values obtained for three difference conformations are referenced to TMS, tabulated above then averaged as before. Similar to the ¹³C Spectrum, a positive deviation from the experimental value is generally observed, take for example in the olefin H. Due to the high sensitivity of the H chemical environment to change with slight conformation change, the values obtained from three conformations tend to be different for most H. Therefore, averaging is important here to give more meaning to the data at this level of calculation.

The basis for assignment is as follows:

• Chemical shifts of methyl carbons are all averaged to give 1 chemical shift due to the fast rotation about C-C bond. In a static picture the methyl H can be vastly different, for example H₄₁, H₄₂ and H₄₃. However, the fast rotation means each proton will experience an averaged environment.
• For those methylene protons which already have similar chemical shifts, such as H₅₀ and H₅₁, they are taken to have the same δ.
• For those that differ considerably, there are two case.
  • Averaging is done if the δ of the two methylene protons exchange values in different conformations. This shows that the difference is only due to conformation interconversion about the methylene group and the H will experience an averaged environment in the dynamic situation. This can be seen in H₃₅ and H₃₆. In the chair conformation, H₃₅ is at ~1.90 ppm and H₃₆ at ~2.40 ppm. However, in the twist chair conformation, H₃₅ is at 1.88 ppm and H₃₆ at 2.68 ppm. Hence, they are likely to interconvert readily to give averaged values that are similar.
  • Averaging is not done if the methylene H cannot rotate easily due to conformational restrictions. This is the case for the cyclopentane methylene protons H_{24, 25} and H_{26, 27}. In all three conformations considered, the chemical shift of the methylene protons differ. Hence, we can infer that the conformation is likely locked and rotation is slow and unlikely. This is also the case for methylene α to C=O. Then, the two methylene protons are not averaged but considered separately.
    
    

By applying the above general tactics and counter checking for any obvious mistakes, the peaks are assigned as the following.

Table 9: Table showing assignment of 1H NMR spectrum against literature and calculated chemical shift values.

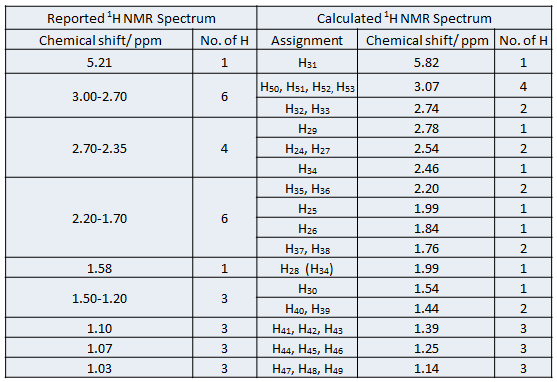
There is undoubtedly error involved due to small number of conformations considered. Yet, considerable confidence can be given to the assignment. In addition, most peak assignments make sense in relation to the position of the H in the molecule. However, the reported triplet at 1.58 ppm (1H) is associated with large uncertainty. Following the general rule above, the peak is assigned to the bridgehead H. Yet this proton is able to couple to 4 neighbouring methylene protons to most likely to a ddt. Examining the molecule, it is most likely to be H₃₄ as it would give the expected triplet. However, the computed chemical shift is 2.46 ppm, almost 1 ppm higher than the reported value if it is assigned to this peak. Yet, as noted in the carbon spectrum above, the S atoms can give rise to large errors in proximal atoms. Therefore, this error might indeed be a limitation with the calculation and the peak should be assigned to H₃₄. However, with this assignment, there is no peak which has chemical shift to the original assignment of H₃₄. Therefore, the original assignment is kept while indicating that H₃₄ is likely at 1.58 ppm. By considering more conformations or using a better basis set, improvement to the current assignment can definitely be made to give a more accurate picture. Despite some limitations, the current method is overall rather useful in helping to gain better understanding of the spectrum.

Analysis on Catalytic Asymmetric Epoxidation

Catalyst Structural Analysis

The development of generalised asymmetric catalyst is highly dependent on the ability to achieve enantioselective substrate – catalyst interaction that is independent on having specific functionality. Therefore, building catalyst with structures that enables intrinsic enantioselectivity based on chiral ligand and steric interactions is crucial. In this section, the crystal structure of two catalysts used for asymmetric epoxidation, Shi and Jacobsen catalysts, were examined to gain a better understanding of their structure. Hopefully this understanding will aid in rationalising their enantioselective mode of action in later discussions.

Shi Catalyst

The C-O bond lengths were examined for any anomeric effect. The diagram below summarises the anomeric effect. As shown, the anti-periplanar arrangement of O_LP and low lying σ*_C-O allows secondary orbital interaction to achieve overall stabilisation. In the extreme case, the orbital interaction can be thought of as resonance forms. From the resonance structures, the effect of anomeric effect on the pair of C-O bond length is shown. The bond length is expected to be very similar if there is similar degree of donation from either oxygen, i.e. degree of blue and red donations are the same. However, the C-O bond length would contract if there is a better donation of its O_LP and poorer acceptance into its σ*_C-O. Conversely, C-O bond lengthens if there is poorer donation of its O_LP and better acceptance into its σ*_C-O. Therefore, in the case where there is unequal degree of donation for the pair of anomeric C-O, one C-O contracts while the other lengthens.

Figure 10: Diagram showing anomeric effect

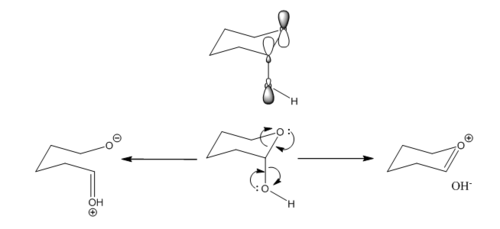
First, it was noted that two conformers are present in the crystal form. One of them have half-boat conformation both ketal ring A and C whereas ring C is almost in perfect envelop conformation in the other conformation. The corresponding C-O bond lengths are difference for the two conformations. Second, it was also noted that the C-O bond length varies considerably across the molecule and between the two C-O in an anomeric pair. The degree of secondary orbital interaction depends on the energy difference between the interaction molecules and the orientation of the orbitals with respect to each other. It is assumed that the energies of O_LP and σ*_C-O are the same for all C-O bonds. Then the difference in C-O bond length can be rationalised mainly by how well the orbitals are aligned for maximum interaction.

Figure 11: Diagram showing numbering of atoms in the molecule and tabulation of C-O bond lengths

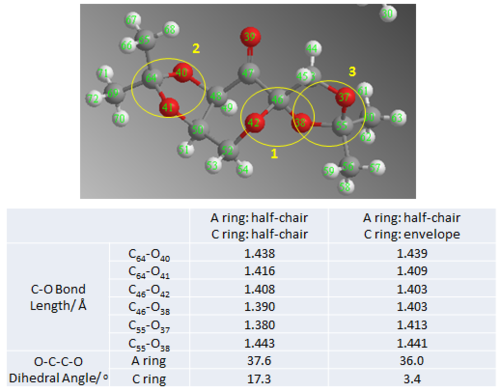
• Conformation 1 (half-chair/ envelop)
  • 1st Pair (O₄₂- C₄₆- O₃₈) @ ring junction
    • The pair of C-O bond lengths are the same and shorter than typical C-O bond length of 1.43 Å. First this indicates that the degree of both possible interactions is very similar. The bond length is very much contracted which is possibly a result of strong orbital interaction which enhances double bonding character. Hence, it could be inferred that the two sets of O_LP and σ*_C-O orbitals are in almost perfect anti-periplanar arrangement.
  • 2st Pair (O₄₀- C₆₄- O₄₁) in A ring
    • The C₆₄-O₄₀ bond length is about 0.03 Å longer than the C₆₄-O₄₁ bond length. Comparing them to typical bond length, C₆₄-O₄₀ is very much contracted while C₆₄-O₄₁ is slightly lengthened. This indicate that there is greater donation from lone pair of O₄₁ into σ* of C₆₄-O₄₀ and very little donation from O₄₀ LP. This is likely due to poor alignment of O₄₀ LP and σ* C₆₄-O₄₁ due to the fixed relative orbital orientation in the half-chair 5-members ketal ring which is more difficult to achieve perfect APP arrangement.
  • 3st Pair (O₃₇- C₅₅- O₃₈) in C ring
    • Similar to the interaction in A ring, the C-O bond lengths are unequal. C₅₅-O₃₇ is shortened by 0.017 Å while C₅₅-O₃₈ is lengthened by 0.011 Å with respect to typical C-O bond length of 1.430 Å. Similarly this indicate that donation from O₃₇ LP into σ* of C₅₅-O₃₈ is better while donation from O₃₈ LP is poorer. Yet, in the envelop conformation, the discrepancy between the two sets of interaction is slightly smaller compared to in the half-chair conformation. This indicates that neither overlap is in ideal APP arrangement for maximum anomeric effect.
      
      

• Conformation 2 (half-chair/ half-chair)
  • 1st Pair (O₄₂- C₄₆- O₃₈) @ ring junction
    • The C-O bond length are now slightly different possibly due to slight repositioning of O₃₈ as ring A goes into a more half-chair conformation. This shifts the orbitals slightly out of alignment such that the set of orbital interaction is unequal. Yet, from the drastic shortening of C-O bond, the anomeric effect between these pair of C-O is still very strong.
  • 2st Pair (O₄₀- C₆₄- O₄₁) in A ring
    • Both ketal ring has slight conformational rearrangement compared to the previous. This can be shown from the change in C-O-O-C dihedral angle. This small conformational rearrangement moved O₄₀ LP and α*C₆₄-O₄₁ slightly out of plane which reduced strength of interaction and a slightly longer bond compared to that in the previous conformation.
  • 3st Pair (O₃₇- C₅₅- O₃₈) in C ring
    • As seen from the much larger change in dihedral angle, there is significant conformation change in the C ring. This resulted in a much better alignment of O₃₇ LP and α*C₅₅-O₃₈ which lead to drastic decrease in C₅₅-O₃₇ bond length. Yet, there is little change in the C₅₅-O₃₈ bond length.
      
      

Therefore, from this conformational analysis, we are able to deduce the relationship between conformational change and degree of anomeric interaction. The effect of varying degree of anomeric effect on C-O bond length has also been accessed to rationalise the difference in C-O bond length across the molecule and when in different conformation. A better understanding and more quantitative analysis of the type and magnitude of interactions could be gained by carrying out an MO analysis to more quantitatively access the energy levels and orbital orientation.

Jacobsen Catalyst

For Mn(Salen) type catalysts used in asymmetric catalysis reactions, such as the Jacobsen catalyst discussed here, the ability to achieve stereoinduction, independent on special functional group interaction, is highly dependent on ligand design . The combined understanding of the catalytic mechanism and catalyst structure is crucial in rationalizing the displayed stereoselectvity. Therefore, the crystal structure of Jacobsen catalyst is analysed here to point out any structural feature that would be of interest in stereoinduction.

Figure 11: Diagram showing crystal structure of Jacobsen catalyst and key structural feature of interest

Referring to Fig. 11, first we note the close approach of the two tBu groups on adjacent phenyl ring. The distance of the closet approach of H on the two tBu groups is 2.421 Å which is equal to twice the Van der Waals radius of H atom. This shows that the tBu group completely blocks off the front face which makes it impossible to approach the catalyst from the front face as indicated below. In addition, the distance of 2.421 Å is highly favourable for attractive H--H interaction. This might help to stabilize the catalyst structure and serve as part of the ‘template’. As the ligand will be attacking the Mn center from the bottom face, where the M=O bond will be positioned upon oxidation of the catalyst, the steric bulk of the tBu also extends below the plane. This further deters the alkene from approaching from the top along the front face.

Next, the role of the other two tBu group is examined. In the space filled model, it was noticed that these two tBu group added steric bulk to the flat phenyl ring to increase steric on the two sides of the catalyst. This steric protection extends to both the top and bottom plane which helps to block access of the alkene from the top face along either left or right side. Overall, the four tBu group are important in selectively increasing steric bulk at specific regions around the catalyst to help induce specific substrate approach. The substrate could then only approach the catalyst from the top along the back there the steric is relatively smaller with the cyclohexane ring.

Lastly, when looking down bottom face of the molecule, the importance of the cyclohexane ring in selective approach of alkene is revealed. Due to the chair conformation of the cyclohexane ring and the stereochemistry at the diimine bridge, one side of the cyclohexane ring is slightly protruding out onto the top plane with an axial H pointing up on the left side. This would aid in selecting the orientation of approaching alkene. As a result, the bulkier substituent will preferentially be placed on the right side where there is less steric hindrance upon approach. In addition, due to the substrate coming from this face, it will be highly unfavourable for trans-alkene to approach with the large substituent approaching in towards the catalyst. Overall, the structure of the ligand is precisely designed to achieve stereoinduction by introducing differential ease of alkene approach. The impact of these will be discussed further together with computational result.

Experimental and Computed NMR Spectrum Comparison

The ¹H and ¹³C NMR spectrum of trans-β-methyl styrene oxide and trans-stilbene oxide have been computed ab initio using Density Function Theory with Gaussian. The NMR spectrum of both (R,R)- and (S,S)- enantiomer have been considered and the results of the calculation is summarised in the table below. The ¹H NMR spectrum obtained experimentally from the epoxidation of the two selected alkenes have been compared to the computed value to assess integrity of the experimentally obtained epoxidation product. As for the ¹³C NMR spectrum, the computed value is compared to reported literature value.

Table 10: Summarised Results for NMR analysis of two epoxides

Categories	(R,R)-trans-β-methyl styrene oxide	(S,S)-trans-β-methyl styrene oxide	(R,R)-trans-stilbene oxide	(S,S)-trans-stilbene oxide
File Type	.log
Calculation Type	FREQ
Solvent	Chloroform
Calculation Method	RB3LYP
Basis Set	6-31G(D,P)
Spin	Singlet
Total Energy	-424.20103221 a.u.	-424.20103221 a.u.	-615.95049738 a.u.	-615.95049737 a.u.
RMS Gradient Norm	0.00001383 a.u.	0.00001382 a.u.	0.00001701 a.u.	0.00001873 a.u.
Dipole Moment	2.25 Debye	2.25 Debye	2.17 Debye	2.17 Debye
Job CPU time	23 min	23 min	1 h 2 min	1 h 1 min
LOG File	File:Rr methyl styrene nmr jq411.log	File:Ss methyl styrene nmr jq411.log	File:Rr stilbene oxide nmr jq411.log	File:Ss stilbene nmr jq411.log
DOI	DOI:10042/28233	DOI:10042/28235	DOI:10042/28234	DOI:10042/28232

Trans-β-methyl styrene oxide

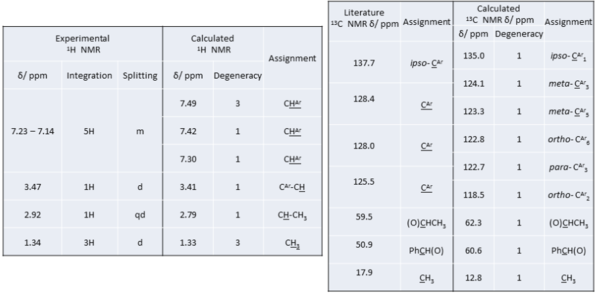
The calculated NMR spectra do not differentiate between the enantiomers. Therefore, the chemical shifts of both enantiomers are the same for both ¹H and ¹³C NMR spectrum. The chemical shifts and assignment have been tabulated.

Table 11: NMR peak summary and assignment

Calculated ¹H and ¹³C NMR Spectrum for Trans-β-methyl styrene oxide

Calculated 1H Spectrum	Experimental 1H Spectrum
Calculated 13C NMR Spectrum

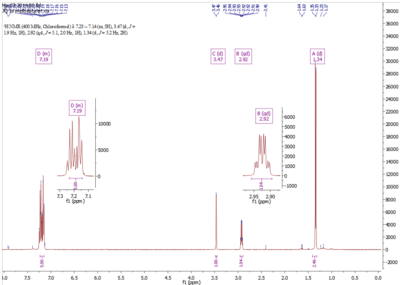
In the ¹H NMR spectrum, there is good general agreement between experimental and calculated chemical shifts. In the aromatic region >7 ppm, both spectrum showed a total of 5 H within close proximity of each other, corresponding to the H of the phenyl ring. The calculated value is however higher than the experimental aromatic chemical shifts. As the experimental is in agreement with literature , the calculation has overestimated the ring current effect on the phenyl protons. The computed value, however, has the advantage of showing more clearly the different types of protons in the ring. This is not shown in experimental spectra as the peaks overlap to give a massive multiplet. In this case, ab initio method can be very useful in helping to understand the subtle difference in electron density at each of the ring proton. In contrast to aromatic ring protons, there is very good agreement between computed and experimental chemical shift. The computed value for the methyl proton is taken as an average of the three due to fast rotation about C-C bond. The limitation of the calculation in this case lies in the lack of information on splitting pattern and coupling constant. Additional computing is required for coupling constant. Yet the experimental spectrum clearly showed the correct splitting. From comparison of the proton NMR spectrum, we are confident that the epoxide prepared experimentally is the expected product although trace amount of impurities were detected.

The agreement between ¹³C NMR chemical shift is slightly poorer than for proton. Yet the general trend is in good agreement. In this case, the computed spectrum is highly useful as it is able to differentiate very similar aromatic C atoms and compute values for each of them. However, due to the limited resolution and general issue of line-width in experimental NMR spectrum, it is not so easy to differentiate the aromatic C other than the quaternary ipso-C. In addition, integration cannot be performed on experimental NMR. Therefore, computational method is very useful in this case to help decipher the spectrum quicker. The chemical shift of the sp³ carbons have been quite well estimated despite relatively large discrepancy between actual values.

Trans-stilbene oxide

Table 12: NMR peak summary and assignment

Calculated ¹H and ¹³C NMR Spectrum for Trans-stilbene oxide

Calculated 1H Spectrum	Experimental 1H Spectrum
Calculated 13C NMR Spectrum

Similar to previous example, there is good general agreement between experimental and calculated chemical shifts. In the aromatic region, there is also an overall overestimation in the computed spectrum. The total number of aromatic protons is consistent in both cases and the experimental value compares well with literature. Once again, it is difficult to see individual aromatic proton peaks in the experimental spectrum. In this case, the protons are not clearly differentiated even for the computed value. This indicates that there is very little difference in the chemical environment about the aromatic protons. A sharp singlet which corrections to the two sp₃ CH at 3.77 ppm on the experimental spectrum showed up expectedly in the computed spectrum at 3.54 ppm. This peak can be used to identify the desired product. Overall, from comparison of the proton NMR spectrum, we are confident that the epoxide prepared experimentally is the expected product.

The agreement between ¹³C NMR chemical shift for trans-stilbene oxide is much better than that for the trans-β-methyl styrene oxide. This might be due to the highly symmetrical chemical environment of the trans-stilbene oxide. By comparing to literature value, it is noted that the accuracy and reliability of the computed value is highly dependent on the molecule. Yet it is still a very useful estimation and tool. From the slight difference in aromatic proton shift and the computed assignment, it could be deduced that the epoxide functionality has slight electron donating effect. The para- and ortho- carbons have slightly higher electron density which corresponds to the effect of electron donating group. The chemical shift of the sp₃ carbons have been very well estimated in this case.

Assignment of Absolute Configuration

Computation of Optical Rotation

The optical rotation for [R,R]-trans-β-methyl styrene oxide, [S,S]-trans-β-methyl styrene oxide, [R,R]-trans-stilbene oxide and [S,S]-trans-stilbene oxide have been computed using DFT method with 6-31G(d,p) basis set. The result of the calculation has been summarised below, along with the computed optical rotation. This section discuss the agreement between the reported optical rotation obtained for the epoxidation product using each of the catalyst and the computed value.

Table 13: Summarised Results for QM Optical Rotation Calculation

Categories	(R,R)-trans-β-methyl styrene oxide	(S,S)-trans-β-methyl styrene oxide	(R,R)-trans-stilbene oxide	(S,S)-trans-stilbene oxide
File Type	.log
Calculation Type	SP
Solvent	Chloroform		Benzene
Calculation Method	RCAM-B3LYP
Basis Set	6-311++G(2DF,P)
Spin	Singlet
Total Energy	-424.07714967 a.u.	-424.07714967 a.u.	-615.76231513 a.u.	-615.76231422 a.u.
Dipole Moment	2.52 Debye	2.52 Debye	2.35 Debye	2.35 Debye
Optical Rotation	+46.77o	-46.77o	+297.93o	-297.76o
Job CPU time	4 h 30 min	4 h 30 min	13 h 5 min	14 h 27 min
LOG File	File:Rr methyl styrene or jq411.log	File:Ss methyl styrene or jq411.log	File:Rr stilbene or benzene jq411.log	File:Ss stilbene or benzene jq411.log
DOI	DOI:10042/28231	DOI:10042/28245	DOI:10042/28225	DOI:10042/28224

The mechanism of catalysis by Shi catalyst has been well studied and computational modelling on transition state has been extensive. Experimentally, the catalyst works well for trans-alkenes at low reaction temperature to achieve high yield and enantioselectivity. For the two chosen alkenes, the major enantiomers produced are [R,R]-trans-β-methyl styrene oxide and [R,R]-trans-stilbene oxide with reported enantiomeric excess (ee%) of 95.5% and 98.9% respectively. The computationally obtained value is compared with the reported experimental value to cross-check the integrity of the two sets of values. The effective optical roatory power of the [S,S]- enantiomers were also reported by Wang et. al when the enantiomer of Shi catalyst is used as catalyst.

Table 14: Summary of calculated and experimental ORP

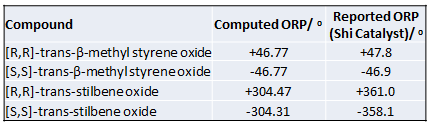
From the table of comparison, there is excellent agreement between the experimentally obtained ORP and the computed value for trans-β-methyl styrene oxide. Not only were the signs of the rotation correctly assigned, even the magnitude of rotation demonstrated a close match. Therefore, by cross-checking, it could be confirmed that the absolute configuration of the corresponding epoxide prepared using Shi catalyst has been correctly assigned. Although there is large difference in the absolute experimental and calculated ORP for trans-stilbene oxide, the estimation is on the same order of magnitude as experimental and the direction of rotation is correctly predicted. This showed that the selectivity of the Shi catalyst has been correctly understood such that the predicted outcome is consistent with the experimental result. In addition, the result from such comparison confirmed the usefulness and reliability of DFT method in simulating and estimating the ORP of small organic system which has large ORP. Therefore, computational method can be used as convenient method to cross-check experimentally obtained result for suitable systems.

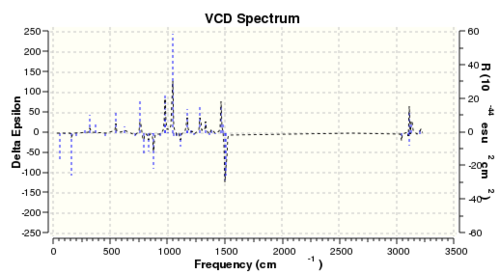
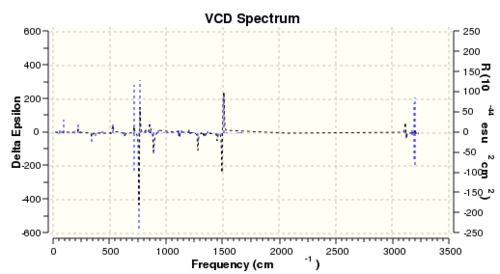
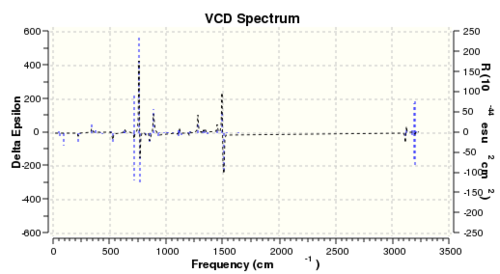
Although not carried out in the experiment, the vibrational circular dichroism (VCD) was also computed using DFT for all four enantiomers to study the difference between the VCD for a pair of enantiomers. The summary of calculation and the computed spectrum is shown in Table 15 and Table 16.

Table 15: Summarised Results for QM VCD Calculation

Categories	(R,R)-trans-β-methyl styrene oxide	(S,S)-trans-β-methyl styrene oxide	(R,R)-trans-stilbene oxide	(S,S)-trans-stilbene oxide
File Type	.log
Calculation Type	FREQ
Solvent	Chloroform
Calculation Method	RB3LYP
Basis Set	6-31G(D,P)
Spin	Singlet
Total Energy	-424.20102040 a.u.	-424.20102040 a.u.	-615.95048946 a.u.	-615.95048946 a.u.
Dipole Moment	2.26 Debye	2.26 Debye	2.17 Debye	2.17 Debye
Job CPU time	34 min	34 min	1 h 25 min	1 h 25 min
LOG File	File:Rr methyl styrene oxide vcd jq411.log	File:Ss methyl styrene oxide vcd jq411.log	File:Rr stilbene oxide vcd jq411.log	File:Ss stilbene oxide vcd jq411.log
DOI	DOI:10042/28226	DOI:10042/28227	DOI:10042/28229	DOI:10042/28228

Table 16: Calculated VCD Spectrum

(R,R)-trans-β-methyl styrene oxide	(S,S)-trans-β-methyl styrene oxide
CAPTION HERE	CAPTION HERE
! (R,R)-trans-stilbene oxide	(S,S)-trans-stilbene oxide
CAPTION HERE	CAPTION HERE

The VCD works on the principle that optically active compound interacts with circularly polarised light differently depending on the polarisation of light. The spectrum displays the difference between absorption of left circularly polarised light (LCPL) and right circularly polarised light (RCPL). Therefore, given that enantiomers differ in their interaction with polarised light, the VCD spectra of a pair of enantiomers will be different. As shown from the computed VCD spectra, there is large difference between the ΔA of the [R,R]- and [S,S]- enantiomer. It was observed that the spectra of a pair of enantiomers have are mirror images of each other about the x axis. Vibration modes, which absorb LCPL more by the [R,R]- enantiomer, will absorb RCPL more by the [S,S]- enantiomer. Therefore, the VCD spectrum is a highly useful method in assigning the absolute configuration of chiral compounds.

Transition State Analysis

The enantiomeric excess is calculated using computed Gibbs Free Energies of the diastereomeic transition state. All QM optimised transition state structure and data have been kindly provided by Prof. Henry Rzepa. The energy of TS leading to each enantiomerically pure product is compared first and the lowest energy TS is used for calculation of ΔG as it is the most energetically favourable one. The equilibrium constant K is then calculated using the Equation 1.

$K=e^{-\mathrm{\Delta }{G}^{\ominus }/(RT)}$ Equation 1

The enantiomeric excess is then estimated from K using Equation 2.

The calculated data is summarised in Table 17.

Table 17: Summary of enantiomeric excess calculation

Shi Catalyst

For reaction catalysed by Shi catalyst, the analysis is broken down such that the TS leading to the same enantiomer is compared. Then the lowest TS leading to [R,R]- or [S,S]- are compared to rationalise the underlying enantioselectivity.

• Trans-β-methyl styrene

The order of transition state in decreasing energy is: (exo/O_axial) > (endo/O_axial) >(exo/O_equatorial) > (endo/O_equatorial). This order is true for transition state leading to either the [R,R]- or [S,S]- product. Therefore, attack with equatorial O of the dioxane is more favourable than attack using the axial O. This could be understood by the transition state conformation of the pyranose ring of catalyst. When equatorial O is involved in attack, the pyranose ring adopts a structure which is close to a chair conformation. In contrast, when the axial O is used, the pyranose ring goes into a half-chair conformation. Analogous to cyclohexane, the half-chair conformation is highly energetically expensive which suffers from both ring strain and torsional strain. Therefore, attach using equatorial O has a lower energy barrier due to less strain imposed on the catalyst in transition state.

Figure 12: Diagrams illustrating preference for attack by equatorial O

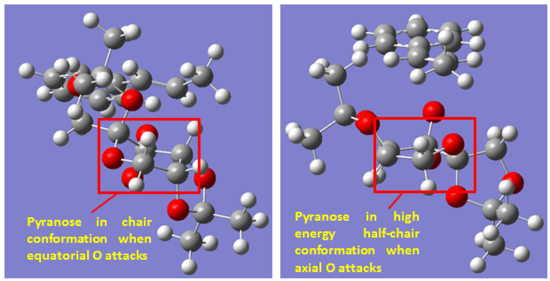
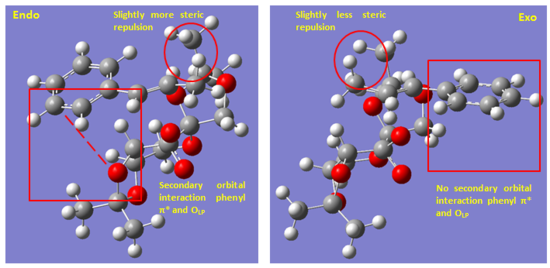
Comparing the two TS which uses equatorial O for attack, the one which involves the endo face of catalyst is lower in energy than when the attack is from exo face of the catalyst. From steric perspective, there is slightly more steric repulsion when attack from the endo face due to the slight closer approach of the alkene methyl group and catalyst methyl group as circled. The difference in steric repulsion was predicted to be small due to the relative flat structure of phenyl ring. Then the difference in TS energy is likely due to secondary orbital interaction that is only possible when attacked from using the endo face. From examination of the structure, the most likely secondary orbital interaction is between the LP of ketal oxygen and the π* orbital of the phenyl ring. This possible interaction is only possible in the endo TS. In addition, there might also be slightly more stabilising non-bonding O--H interactions in the endo TS. This is true for the two TS which both uses the axial O for attack as well. Therefore, the bias towards endo TS is likely due to stabilising secondary orbital interaction. Overall, the conformational distortion of the catalyst in TS is a more important factor than the secondary orbital interaction. The destabilizing effect of having a half-chair conformation is estimated at ~24 kJ/mol while the stabilizing effect of secondary orbital interaction is ~8 kJ/mol by comparing the energies of TS. Therefore, biasness towards equatorial O is greater than biasness towards endo face.

Figure 13: Diagrams illustrating preference towards endo- approach of catalyst

As the same trend is observed for the [S,S]- TS as well, we move on to assess the difference in stability between the lowest energy [R,R]- TS and [S,S]- TS to explore possible reason for enantioselectivity. From the calculation, the lowest energy [R,R]- TS is 25.4 kJ/mol lower than the lowest energy [S,S]- TS. This converts to an ee% of 99.94% which is slightly higher than the experimental value of 95.5%. This indicate that there is a slight overestimation of the energy difference between the lowest energy [R,R]- TS and [S,S]- TS using the computational method. Yet, the selectivity is correctly predicted and consistent with experimental result.

Figure 14: Diagrams illustrating preference for Re face

As these two TS both involve chair conformation TS and endo attack, the main difference lies in the difference in steric hindrance at TS. Evidently shown on Fig. 12, there is much greater steric repulsion in the [S,S]- TS between the alkene methyl group and the methyl group of the catalyst in a head-on fashion. In the [R,R]- TS, the same position is occupied by much smaller alkene H. In addition to this steric term, the alignment of phenyl ring and the O_LP is much poorer in the [S,S]- TS as the phenyl ring is pointed away from the catalyst. Therefore, there is overall kinetic biasness towards [R,R]-trans-β-methyl styrene oxide which results in the observed enantioselectivity.

• Trans-stilbene

The order of transition state in decreasing energy is: (endo/O_axial) ~ (exo/O_axial) >(endo/O_equatorial) ~ (exo/O_equatorial). Due to the symmetry of trans-stilbene, there is very little biasness towards which face of the catalyst is involved. The energy difference between (exo/O_equatorial) and (endo/O_equatorial) is only 0.36 kJ/mol. The difference is only due to the way in which the plane of the phenyl ring is twisted. When catalyst attacks from the exo face, the plane of the phenyl ring closer to the catalyst is twisting away while it is twisting towards the catalyst in the endo TS. Therefore, the endo and exo selectivity is reversed here. However, due to the small energy difference, it is possible that both pathway is almost equally likely. The same selectivity towards the equatorial O is shown here. The strain which is associated with a half-chair catalyst in the TS when axial O is used in attack holds true for both alkenes. Therefore, we can generalise that for Shi catalyst catalysed epoxidation reaction, the equatorial O is always the one involved in attack of alkene C=C.

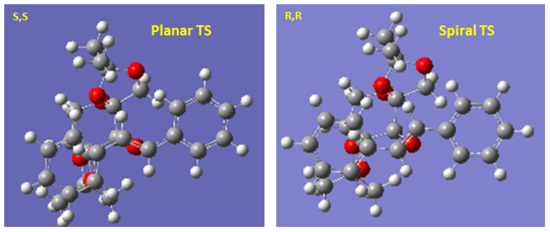
The energy difference between the lowest energy [R,R]- and [S,S]- TS is 16.8 kJ/mol in this case. This computes to a ee% of 99.73% which is also a slight overestimate of the experimental value. Once again, the predicted selectivity towards [R,R]-trans stilbene oxide is consistent with the experimentally observed selectivity. Different from the example of tran-β-stilbene, the energy difference in this case is a result of secondary orbital interaction rather than sterics. The [R,R]- TS is a spiral while the [S,S]- TS is planar. As previously reported by Bach and co-worker , a stabilizing secondary orbaital interaction between O_LP and the π*_C=C is only present in the spiral TS. In addition, this effect grows as the bond forming process becomes more asynchronous which is the case here . Therefore, the [R,R]- TS benefits from this stabilizing interaction with spiral geometry. Therefore, there is also overall kinetic biasness towards [R,R]-trans-stilbene oxide which results in the observed enantioselectivity.

Figure 15: Diagrams illustrating spiral and planer TS

Jacobsen Catalyst

• Trans-β-methyl styrene

From examination of the transition state structure, there are two types of interactions contributing towards enantioselectivity. Between TS leading to the same enantiomer, the selectivity is based on steric repulsion. Between the lowest energy [R,R]- and [S,S]- TS, the selectivity is achieve through different extent of stabilizing π stacking. Among the four possible transition states, the ([S,S]-/endo) TS benefits the greatest π interaction and suffers the least steric hindrance. Therefore, [S,S]-trans-β-methyl styrene is formed with a predicted 97.77% ee.

Figure 16: Diagrams comparing four possible transition states with key interactions highlighted

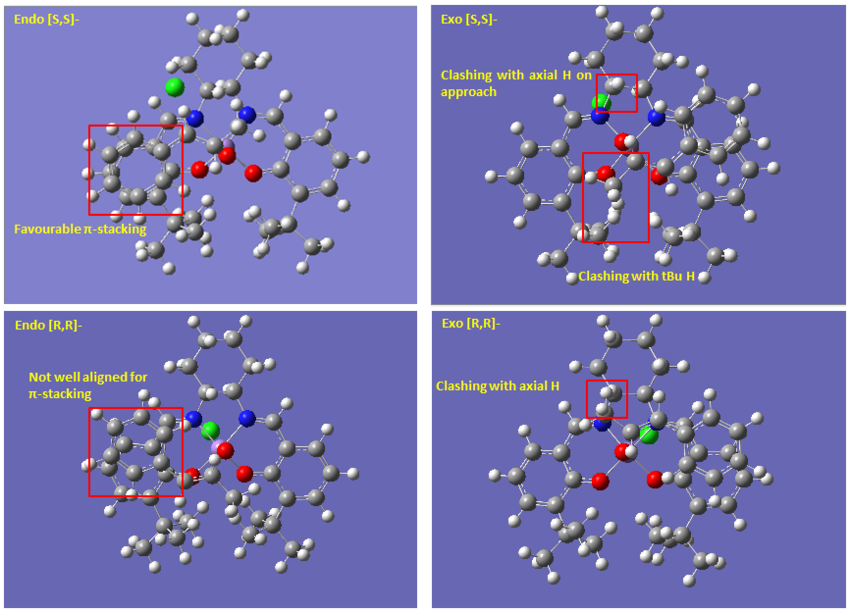
Comparing the TS leading to the same enantiomer, the selectivity between the two possible TS is influence by steric hindrance involved during substrate approach . Due to the catalyst structure discussed previously, substrate approach is only possible from the top along the cyclohexane ring. Due to the chair conformation of the ring, the axial H closest to metal center can impose steric hindrance on approaching alkene. The steric bulk of methyl and phenyl group are similar in this trajectory. However, the flat structure of phenyl ring means that when the alkene approaches the catalyst with phenyl group closer to the axial H would suffer less steric hindrance. This contribution alone ~1.5 kJ/mol, which is small as expected, comparing the energy of the two [R,R]- TS. However difference between the [S,S]- TS is much greater than this. In addition to sterics, the endo [S,S]-TS benefits from almost perfect π stacking which is lacking in the exo [S,S]- TS. The selectivity between [S,S]- and [R,R]- product is also due to this interaction. This overlapping of π electron cloud of substrate and ligand contributes about 11.05 kJ/mol by comparing endo [S,S]- and endo [R,R]- TS. Combination of steric and π stacking beautifully explains the energy difference of 12.2 kJ/mol between the endo and exo [R,R]- TS.

• Trans-stilbene

First, we note the small energy difference between TS leading to [R,R]- and [S,S]- product which resulted in much poorer selectivity and ee of only 76.73% was computed from the energy difference of 7.6 kJ/mol. This energy is on the same order as the thermal fluctuation. Therefore, selectivity is very poor. It is only when the reaction is run at low temperature could the selectivity be improved.

Examining the TS geometry, neither TS benefit from any significant π-stacking. In addition, due to symmetry of the molecule, the steric repulsion is very similar in both cases. The only slight difference might be due to repulsive interaction of alkene H with tBu H of the ligand. In the [R,R]- TS, the closest approach of these two H is 1.985 Å. This distance is alightly longer at 2.021 Å in the [S,S]- TS. Although the this difference in length is not huge but non-bonding Van der Waals interaction increases exponentially beyond 2.1 Å for H--H. Therefore, this might be the major contribution towards enantioselectivity. However, since this term is relatively small and no other significant biasness can be found, the energy difference between the two TS is small as well. Therefore, for catalyst of which enantioselectivity depends on non-specific/ non-functional group interaction, selectivity could be severely affected by highly symmetrical substrate.

Figure 17: Diagrams illustrating preference for [S,S]- TS

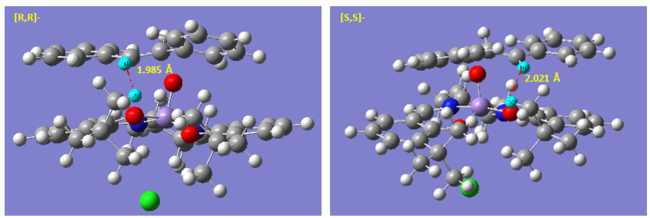
Additional Information and Analysis on Transition State

Non-Covalent Interaction Analysis

To better understand the interaction between catalyst and substrate at transition state, non-covalent interaction analysis was carried out for the most stable transition state for trans-β-methyl styrene with Shi catalyst which involves attack on Re face, by equatorial O and endo- catalyst approach. The transition state calculation and method used to visualise NCI surface has been kindly supplied by Prof. Henry Rzepa. The visualised NCI is shown below.

Isomer 1

At the region where new bond is formed between the oxygen of catalyst and the alkene C=C, there is mixed highly repulsive and attractive interaction as shown by the ring of mixed red (highly repulsive) and blue (highly attractive) indicator. However, this region does not contribute towards the NCI between catalyst and substrate which we are interested in. There is considerably large area of mildly attractive interaction near the region where the alkene methyl substituent and the methyl group of the ketal ring on the catalyst are located. This attractive Van der Waals interaction between the H on the methyl groups of substrate and alkene was already envisioned in the analysis of the transition state by looking at the distance between non-bonding H atoms on the catalyst and the substrate. However, looking at the distance only gave a localised picture of each individual interaction. In contrast, in the visualised NCI surface, we can see that several attractive NCI in close proximity of each other has been considered together. Therefore, a more collective picture was shown to give a semi-quantitaive sense of the extent of such interaction. In addition to this region with large extent of mildly attractive interaction, there is also some attractive interaction between the phenyl ring and the catalyst. The interaction between ketal O and the phenyl ring above it, which was proposed in earlier section, is shown here as well.

Figure 18: Comparing NCI surface for lowest energy transition state leading to [R,R]-and [S,S]-trans-β-methyl styrene oxide

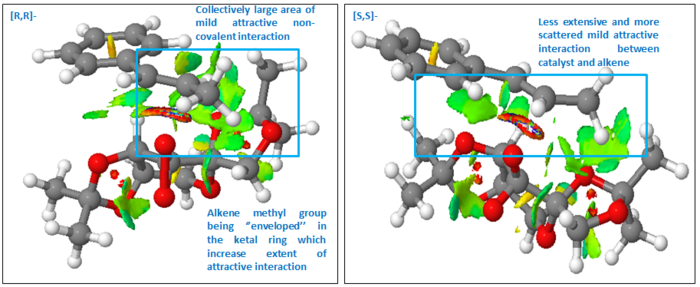
It then becomes most useful to compare the NCI in the lowest energy [R,R]- and [S,S]- transition state to validate and check our earlier proposal about the mode of enantioselectivity of Shi catalyst. Earlier, it was proposed that the discrimination lies in the repulsion between methyl groups on substrate and catalyst in the [S,S]- TS. However, examining the NCI surface, despite the short distance between the methyl groups measured earlier, there is actually mildly attractive interaction between them. This shows that the previous proposal for enantioselectivity is not correct. Comparing the two TS, it becomes immediately apparent that there is much larger attractive NCI surfaces in the [R,R]- than [S,S]- TS. This is due to the relative orientation of the catalyst and the substrate in [R,R]- TS such that there are greater area of contact between non-bonding H atoms. The alkene methyl group is somewhat enveloped in the ring ketal group at an attractive distance. The additional information which NCI surface can provide is highly useful in determining the contribution of NCI towards stability at transition state. It provides a semi-quantitative picture which just by looking at non-bonding distance does not provide.

Investigating the Electronic Topology (QTAIM) of Active Site

QTAIM provide information on both covalent and non-covalent interactions and the position of bond critical point (BCP). Such information can be complementary to the NCI analysis and QTAIM analysis was carried out for the lowest energy [R,R]- TS for trans-β-methyl styrene to cross check how it agrees with the result of NCI surface visualisation.

First, we looked for non-covalent interaction about the region where there has mildly attractive NCI as previously pointed out in the NCI surface. Indeed, the QTAIM also showed pairs of non-covalent interaction, indicated by dotted line, between the methyl H of the alkene and the catalyst. Interaction between the ring junction H of catalyst and ipso-C of phenyl group is also indicated. In addition, the forming C-O bond between the active catalyst and the alkene is also reflected. We can see that the bond forming step is asynchronous as one C-O bond is formed first at TS. Different from NCI surface, only the number of interacting pair is given, not the extent and the collective effect. Yet, it gives a clearer picture of which non-bonding atoms are responsible for the interaction shown in NCI surface.

Figure 19: Screenshot of QTAIM analysis for lowest energy transition state leading to R,R]-trans-β-methyl styrene oxide

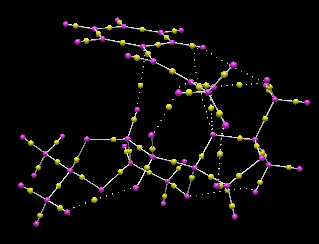
For non-covalent interaction between non-bonding H, the BCP is located almost equal distance to the two H atoms involved. For non-covalent C--H interactions, the BCP is located slightly nearer to the H atom. The location of BCP in the covalent bonds is rather interesting as summarised in point form below.

• BCP is located mid distance for σC-C bond
• Location of BCP for σC-H bond depends on what atom the C is bonded to.
  • It is located nearer to H when the carbon is not bonded to any heteroatom.
  • It is located nearer to the C when the C is also bonded to O atom, such as the carbons in the ketal ring.
• BCP is located nearer to C atom for σC-O bond

Figure 20: Diagram showing proposed relationship between location of BCP along a single covalent bond and atom contribution towards bond localised MO

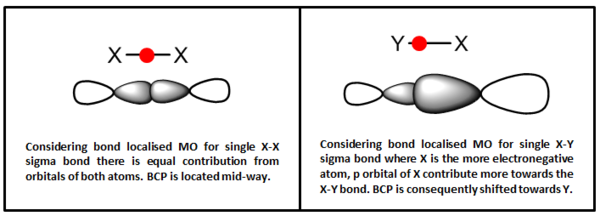
From these observations, we can generalise that the BCP is generally located nearer to the more electropositive atom in a heteronuclear bond. When carbon is bonded to electronegative heteroatom, the electron density on it is greatly reduced that it is slightly more electropositive than the H it is bonded to which shifts the BCP towards itself. Considering bond localised molecular orbital, the BCP could be seen as the location of maximum electron density between the two bonding atom. As more electronegative atom contribute more towards bonding orbital, the lobe of its orbital will ‘extend pass’ the mid-point of the X-Y bond. Then the location where the two orbital overlaps and achieves maximum electron density is slightly closer to the more electropositive atom. Hence, from the location of the BCP, we can deduce the contribution of each atom’s orbital towards a single covalent bond. In an X-Y bond, the further the BCP is located from X, the greater contribution X has towards the X-Y bond.

Possible Epoxide Candidate

In this experiment, all the alkenes are disubstituted. Hence, it might be interesting to investigate trisubstituted alkene. This might better demonstrate the selectivity of Shi catalyst and the interaction of substrate with the catalyst in spiral transition state. Or it might be interesting to investigate spiral vs. planar transition state for trisubstituted alkene to discuss the more favourable or equivalent pathways. As such, I would suggest trans-α-methylstilbene. Literature material is readily available and for Shi catalyst it would give (R,R)-2-Methyl-2,3-diphenyloxirane selectively . The optical rotation for this molecule has been reported to be +113.9^o . The molecule is also relatively small which means it will be suitable for computational purpose in 3rd year lab.