Rep:Mod:jhm2017
Introduction to Molecular Modelling 2 - Harry Moore
NH3 Molecule
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -56.55776873 a.u.
Point Group: C3V
Bond Length: 1.01798 Angstroms
HNH Bond Angle: 105.74115 Degrees
Item Table - NH3 Optimisation
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986274D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
NH3 JMOL file
NH3 |
The optimisation file is linked here
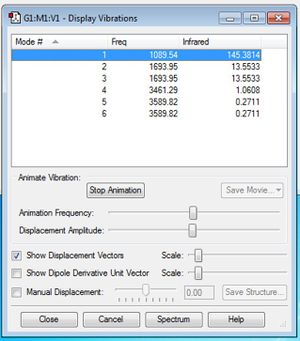
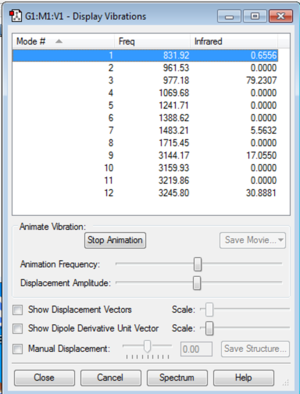
NH3 Frequency Analysis
From the 3N-6 rule, applied to non-linear molecules, we would expect 3(4)-6=6 vibrational modes.
Modes 5 and 6 are degenerate, as are modes 2 and 3
Modes 1-3 are bending, whilst modes 4-6 are stretching vibrations.
There are two symmetric vibrations - mode 4 is the highly symmetric stretch, mode 1 is the 'umbrella' bend, which is similarly symmetric.
There would be 4 bands shown in a gaseous IR spectrum equating to each of the four different expected vibrational frequencies. However there are only 2 expected peaks due to the very minimal change in dipole moment in two of the vibrations, hence low intensity absorbtion at these frequencies.
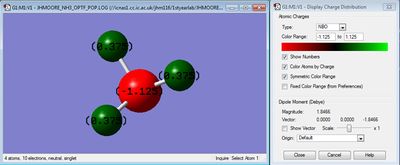
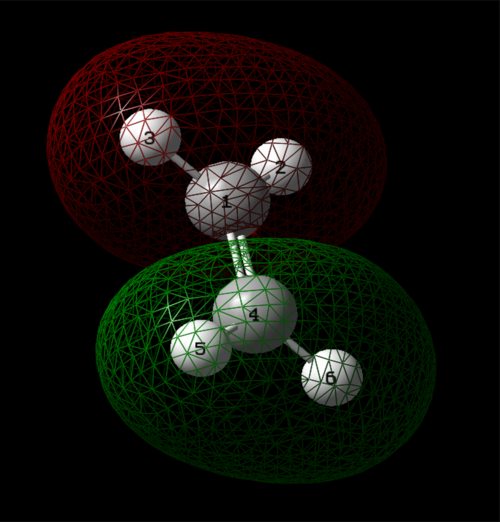
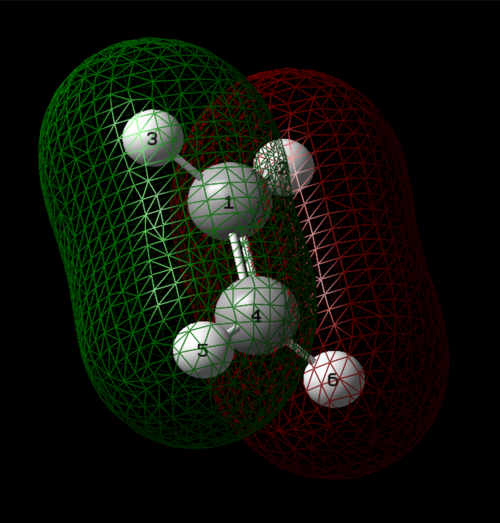
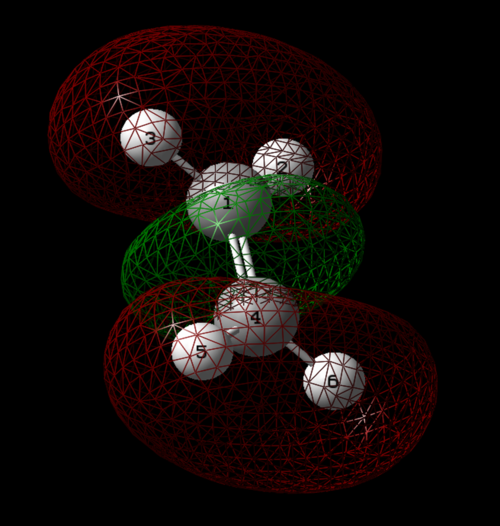
Atomic Charges
Based on the electronegativity difference between nitrogen and hydrogen, the nitrogen atom is expected to take a negative charge, whilst the hydrogens take a positive charge.
Nitrogen had a charge of -1.125, whilst hydrogens had a charge of 0.375.
Haber-Bosch Process
N2 Computations
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -109.52412868 a.u.
Point Group: D∞h
Bond Length: 1.10550 Angstroms
H-H Bond Angle: 180 Degrees
The summary of the Gaussian output file is shown below:
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000002 0.001800 YES
RMS Displacement 0.000003 0.001200 YES
Predicted change in Energy=-1.248810D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The full optimisation file for N2 is linked here
N2 JMOL file
N2 |
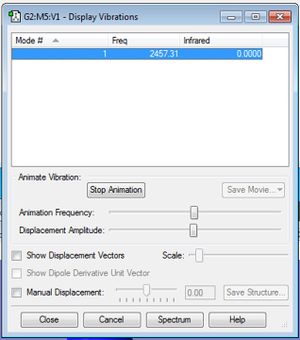
N2 Frequency Analysis
Linear molecule gives 3N-5 vibrational modes, hence just one symmetric stretch possible. This would not be visible on IR spectrum due to the lack of changing dipole moment. Below is the output for the calculated vibration:
Since there is no dipole moment due to being homonuclear, there is no expected IR wavenumber as there is no change in net dipole moment upon vibration.
H2 Computations
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -1.17853931 a.u.
Point Group: D∞h
Bond Length: 0.74307 Angstroms
Bond Angle: 180 Degrees
The summary of the Gaussian output is shown below:
Item Value Threshold Converged?
Maximum Force 0.000199 0.000450 YES
RMS Force 0.000199 0.000300 YES
Maximum Displacement 0.000262 0.001800 YES
RMS Displacement 0.000370 0.001200 YES
Predicted change in Energy=-5.194630D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7431 -DE/DX = -0.0002 !
--------------------------------------------------------------------------------
The optimisation file for H2 is linked here
H2 JMOL File
H2 |
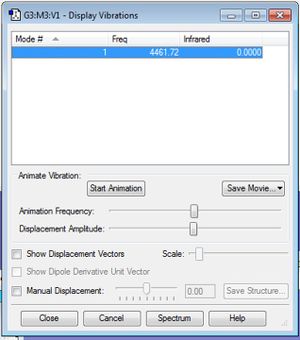
H2 Frequency analysis
Hydrogen produces one vibrational mode also, where the output is shown below:
Similarly to Nitrogen, this symmetric vibration leads to no net change in dipole moment, hence no absorptions would be visible to IR spectrometer
Reaction Energy
The Haber Bosch process is the reaction between nitrogen and hydrogen gas to produce ammonia, used, among other things, as a fertiliser. The industrial process has been optimised to balance rate of reaction and position of equilibrium with safety and economy.
Energy Values in a.u:
E(NH3)= -56.55776873
2*E(NH3)= -113.1155375
E(N2)= -109.52412868
E(H2)= -1.17853931
3*E(H2)= -3.53561793
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579089 au
Energy Values in KJ/mol
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.478992853 kJ/mol
ΔE= -146.48 kJ/mol
Since the reaction is exothermic, the ammonia is more stable than the reactants, as the energy released forming bonds exceeds that required to break those of the reactants.
This compares to an enthalpy change of -46.2 KJ/mol for the industrial process. This discrepancy is likely due to the conditions used in the industrial Haber process, with pressures up to 350 bar, and temperatures of around 500 celcius[1]. These deviate from the enthalpy change expected under standard conditions.
Methane Calculation
Optimisation Summary
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -40.52401401 a.u.
Point Group: Td
Bond Length: 1.09203 Angstroms
HCH Bond Angle: 109.47122 Degrees
The summary of the output file is shown below
Item Value Threshold Converged?
Maximum Force 0.000057 0.000450 YES
RMS Force 0.000016 0.000300 YES
Maximum Displacement 0.000089 0.001800 YES
RMS Displacement 0.000037 0.001200 YES
Predicted change in Energy=-5.694725D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.0919 -DE/DX = 0.0 !
! R2 R(1,3) 1.0919 -DE/DX = 0.0 !
! R3 R(1,4) 1.0919 -DE/DX = 0.0 !
! R4 R(1,5) 1.0918 -DE/DX = 0.0001 !
! A1 A(2,1,3) 109.4708 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4708 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4739 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4658 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.473 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.473 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -119.9959 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0022 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0022 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 119.9956 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The full output file is linked here
CH4 JMOL File
CH4 |
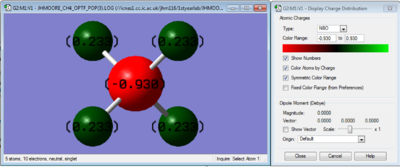
CH4 Charge Distribution
The small difference in electronegativity between carbon and hydrogen leads to an overall positive charge on the hydrogens (+0.233), and a negative charge on the central carbon (-0.930)
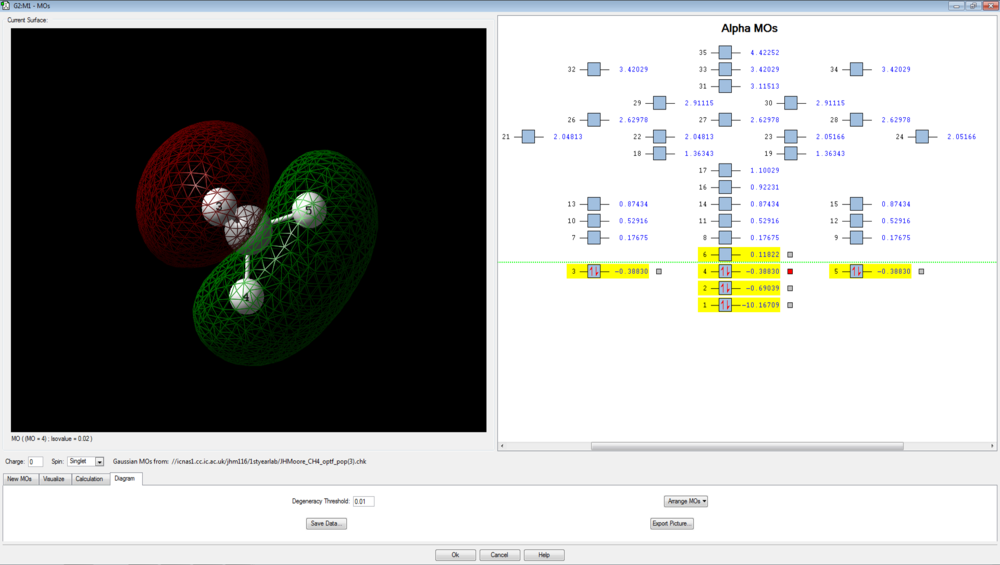
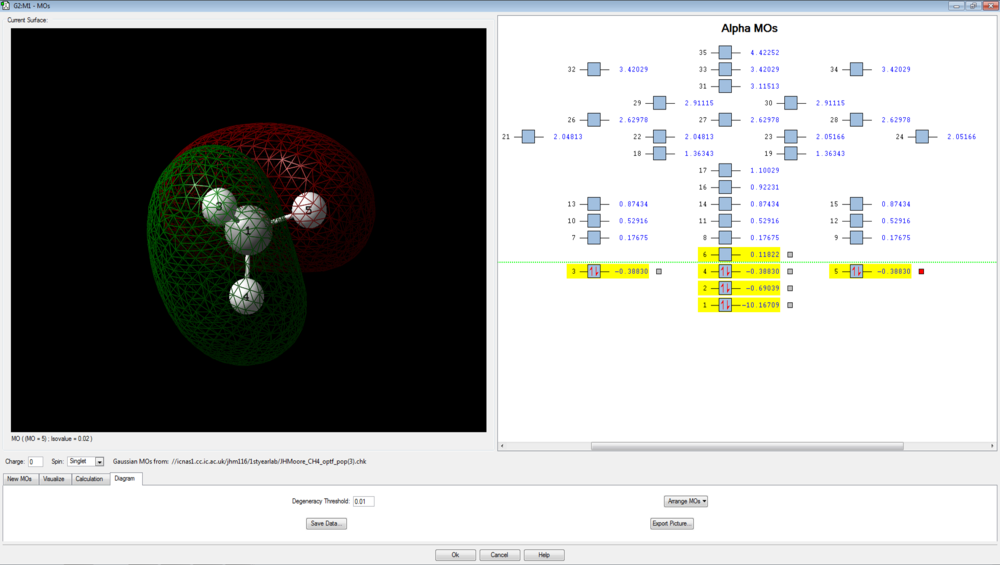
Molecular Orbital Modelling
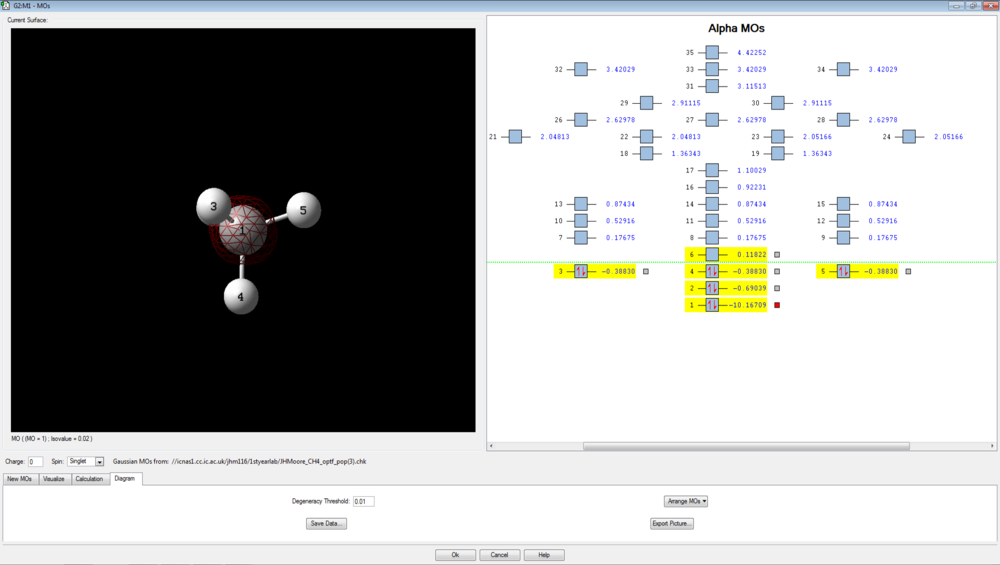
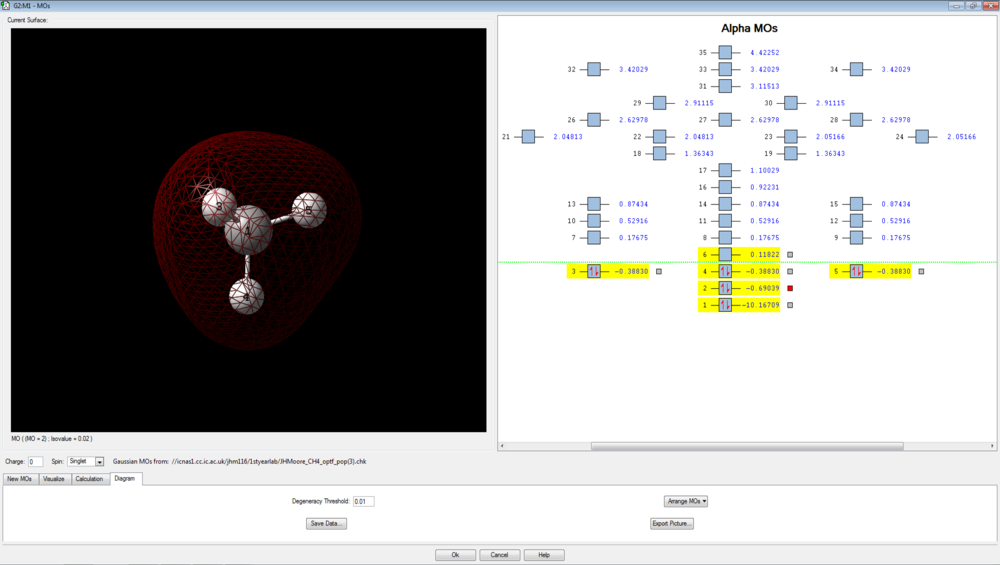
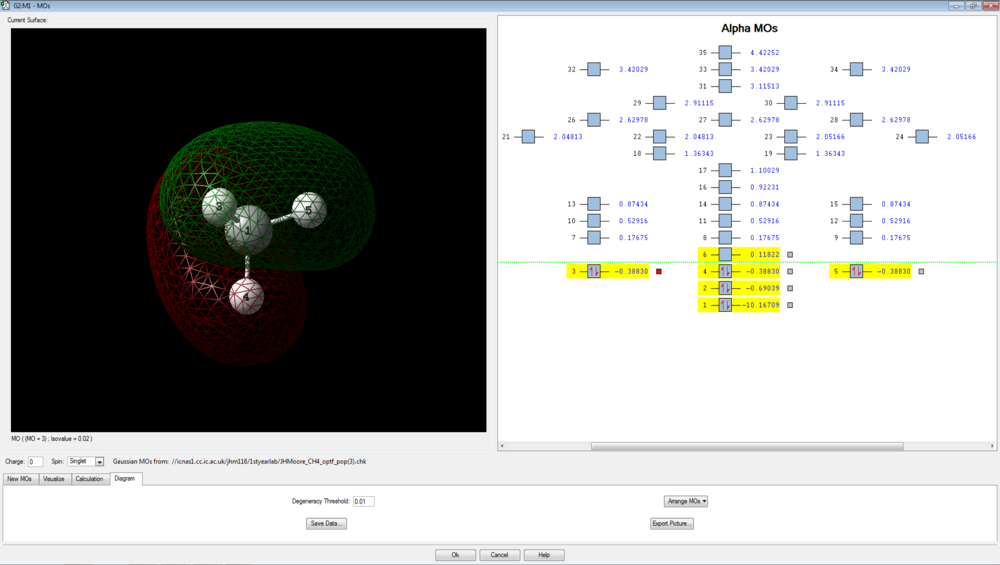
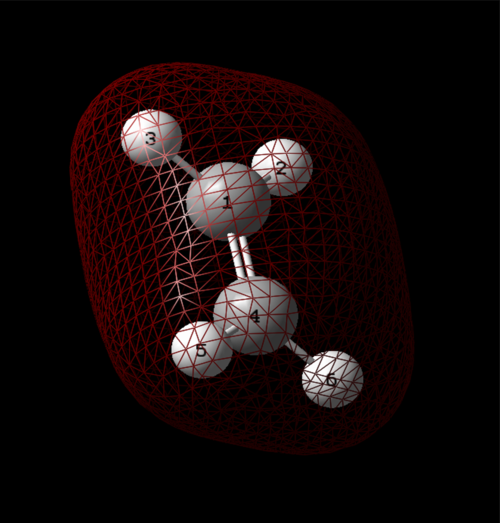
There are 4 bonding molecular orbitals, of which three are degenerate, and one non-bonding orbital. These are shown below.
The first is the 1s of carbon, which is not involved in bonding and does not interact with other orbitals since it is very deep in energy, calculated to be -10.16709 au. This is the non-bonding orbital.
The first orbital to interact with other hydrogenic 1s orbitals is the hydrogen 2s, since it is less deep in energy than the 1s shown above. This forms a symmetrical orbital that covers the entire molecular skeleton. It has an energy of -0.69039 a.u.
The final three orbitals are all degenerate, with energies of -0.38830 a.u. These are degenerate due to the orthogonal (degenerate) p orbitals of the carbon interacting with hydrogen 1s orbitals. The evidence for the p-orbital is given by the nodal plane that exists through the central carbon. These three degenerate orbitals are the HOMOs of methane:
Additional Molecular Calculation - Ethene
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -78.59380796 a.u.
Point Group: C2H
Bond Length (C=C): 1.33008 Angstroms
Bond Length (C-H): 1.08674 Angstroms
Bond Angle (H-C-H): 121.81681 Degrees
HCH Bond Angle: 109.47122 Degrees
Item Table
Item Value Threshold Converged?
Maximum Force 0.000107 0.000450 YES
RMS Force 0.000040 0.000300 YES
Maximum Displacement 0.000168 0.001800 YES
RMS Displacement 0.000092 0.001200 YES
Predicted change in Energy=-2.636301D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.0867 -DE/DX = -0.0001 !
! R2 R(1,3) 1.0867 -DE/DX = -0.0001 !
! R3 R(1,4) 1.3301 -DE/DX = 0.0001 !
! R4 R(4,5) 1.0867 -DE/DX = -0.0001 !
! R5 R(4,6) 1.0867 -DE/DX = -0.0001 !
! A1 A(2,1,3) 116.3631 -DE/DX = 0.0 !
! A2 A(2,1,4) 121.8168 -DE/DX = 0.0 !
! A3 A(3,1,4) 121.8201 -DE/DX = 0.0 !
! A4 A(1,4,5) 121.8168 -DE/DX = 0.0 !
! A5 A(1,4,6) 121.8201 -DE/DX = 0.0 !
! A6 A(5,4,6) 116.3631 -DE/DX = 0.0 !
! D1 D(2,1,4,5) 180.0 -DE/DX = 0.0 !
! D2 D(2,1,4,6) 0.0 -DE/DX = 0.0 !
! D3 D(3,1,4,5) 0.0 -DE/DX = 0.0 !
! D4 D(3,1,4,6) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The full optimisation file is linked here
Vibrational Analysis
Ethene produces 12 different vibrations, of which 4 produce detectable absorptions due to a net change in dipole moment. The absorption with intensity of 0.6556 would be difficult to detect in reality.
Molecular Orbital Analysis
Five of the molecular orbitals for ethene are shown below. The first is a non-bonding orbital, the rest are bonding orbitals.
One of two non-bonding orbitals is shown here, from the carbon 1s atomic orbital, which is sufficiently deep in energy to avoid interaction. Here, both orbitals have the same phase. The energy is -10.18441 a.u.
The next MO is from the interaction of the 2s carbon AO with the 1s of each of the hydrogens. In a similar way to methane, this MO covers the entire molecular skeleton. The energy is -0.75518 a.u.
This is the combination of the 1s hydrogenic orbitals with the carbon 2s. The orbital is bonding with respect to each end of the molecule, and antibonding with respect to the C=C bond i.e. the two carbon 2s AOs are in antiphase. The energy is -0.57651 a.u.
This is the first MO to feature a nodal plane on an atom, hence the first to feature a p-orbital of the carbon. This p-orbital is in the plane of the C-H bond, hence the plane down the centre of the molecule. The energy is -0.46398
This MO is due to the p-orbital in line with the C=C bond. The outer lobe of the orital is in phase with each of the hydrogen 1s orbitals adjacent to it, and the lobe of opposite phase is in phase with the equivalent lobe of the other carbon, creating nodal planes on each carbon.
References
[1] - Appl, M. 2011. Ammonia, 2. Production Processes. Ullmann's Encyclopedia of Industrial Chemistry