Rep:Mod:jhb79574592
Computational Lab Spring 2009 - Module 1 - James H. Bannock (CID: 00468630)
Notes
- This wikipage has been designed on and optimised for the Safari browser.
- Jmol pop-up's DO NOT work in Internet Explorer (possibly a pop-up blocking fault!). Firefox and Safari do allow Jmol applets to initiate.
Molecular Mechanics (MM2)
MM2 optimisation is classical mechanics approach to optimising the structure based on electrostatic interactions. The optimisation works by minimising destabilising interactions like bending or Van der Waals forces, and maximising the stabilising from dipole/dipole interaction. This method is a good starting point for optimising molecules but it can in no way predict certain reactivity as will be shown later on in the project.
Cyclopentadiene[1]
Part a) Dimerisation of cyclopentadiene:
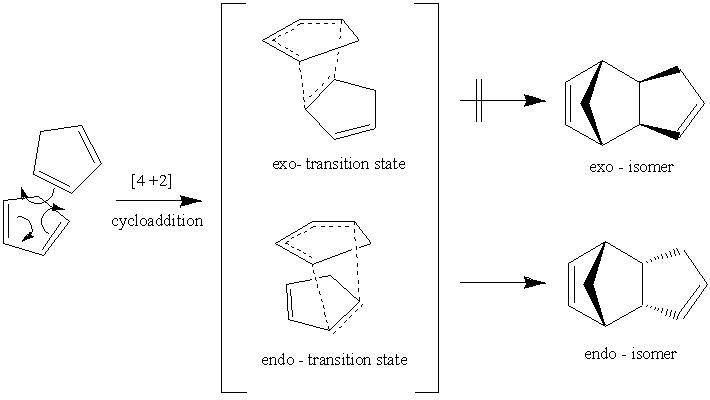
Cyclopentadiene can undergo a [4+2] cycloaddition dimerisation to form dicyclopentadiene, Scheme 21a1s. (below). In general cycloaddition reactions proceed to form either endo- or exo- isomers or a mixture of the two. It is known for the dimerisation of cyclopentadiene the endo- isomer forms almost exclusively and the exo is only formed upon considerable heating (i.e. thermal activation).
Using molecular mechanics, the thermal stability of the products has been determined to a good degree of accuracy. The method employed was a MM2 energy minimisation in ChemDraw3D Ultra with an RMS (rate of change of energy with nuclear position) set to 0.0001 to ensure the output energy was as close to the equilibrium energy (i.e. the bottom of the potential well). In an ideal case the RMS would equal zero, however the RMS was set to 0.00001 and no significant effect on the output energy was observed compared to the former RMS value tested. The ground state energy of cyclopentadiene was computed using the same method, resulting in an ground state energy of 6.3895kcal/mol. Thus in a 2:1 reaction of cyclopentadiene:dicyclopentadiene the sum of the energy of the reactants is equal to 12.779kcal/mol. Table 21a1T details the results of this optimisation.
| Energy Type | Exo-isomer Energy kcal/mol | Endo-isomer Energy kcal/mol |
|---|---|---|
| Jmol pop-up | ||
| Stretch | 1.2850 | 1.2509 |
| Bend | 20.5804 | 20.8476 |
| Stretch-Bend | -0.8381 | -0.8358 |
| Torsion | 7.6555 | 9.5110 |
| Non-1,4 VDW | -1.4174 | -1.5437 |
| 1,4 VDW | 4.2334 | 4.3199 |
| Dipole/Dipole | 0.3775 | 0.4476 |
| Total Energy | 31.8764 | 33.9975 |
Analysis of the results in Table 21a1T (above), indicates that for both product isomers the energy is higher than the sum of the reactant ground state energies. It is therefore plausible to suggest that the cycloaddition is endothermic in this case. The molecular mechanics takes into account enthalpic effects, not entropic, but it is well documented[ref] that pericyclic processes require heat or light provide the energy required to drive the reaction, so it can be assumed that entropy is a minor contributor to the Gibb's free energy. Addition of of heat to the system (i.e. thermal activation) will increase the effect that the entropy has on the system by the the Gibb's free energy equation, Equation 21a1E (below). Illumination (photo-activation) can trigger processes which bypass the standard dark chemistry model (therefore disregarding the activation barrier) and allow for example radical mechanisms to proceed.
The results indicate the exo-isomer is 2.1211kcal/mol more stable. The difference in energy is largely accounted for by torsion energy, this energy does not represent a physical property it is better described as a fitting factor to match calculated energies with Quantum Mechanics at a given dihedral angle. In this case consideration of the sterics best resolves the question of energy differences. If the mechanism was under thermodynamic control this isomer would dominate the endo-isomer (under equilibrium control). However, this is not the case. It is known that the reaction proceeds to form the endo-isomer exclusively. This is evidence that the reaction is under kinetic control. This result means that molecular mechanics cannot be used to predict the reaction mechanism as it is controlled by the transition state (kinetic control). The molecular mechanics method can only be used if the reaction is under thermodynamic control and hence cannot predict transition state conformations.
Kinetic Explanation:
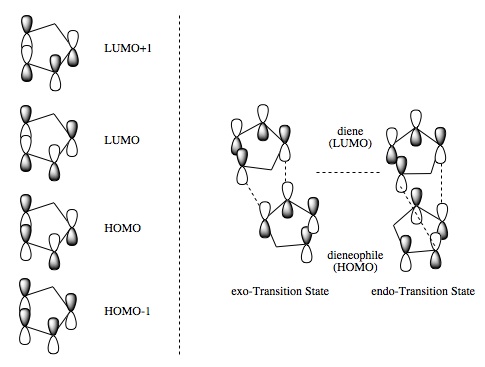
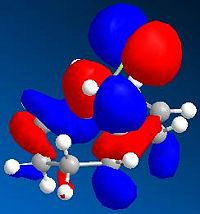
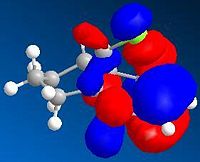
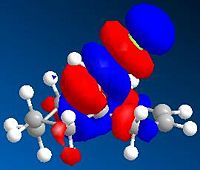
Figure 21a1F shows the four molecular orbitals (also computed, Table 21a2T (below)). The dimerisation occurs via overlap of the HOMO (Highest Occupied Molecular Orbital)of the dienophile with the LUMO (Lowest Unoccupied Molecular Orbital) of the diene. Both isomers result in good overlap between molecules, however in the endo-transition state there is increased stability caused by secondary orbital overlap between the two sets of orbitals adjacent to those previously mentioned. This overlap has no effect on the product but it lowers the 'activation energy' of the reaction, a kinetic phenomena, thus the endo-isomer predominates in the reaction mixture.
| HOMO-1 | HOMO | LUMO | LUMO+1 |
|---|---|---|---|

|

|
|

|
It is clear that the computed MOs in Table 21a2T are not the same as in Figure 21a1F. This is because the LCAO (Linear Combination of Atomic Orbitals) approach used in Figure 21a1F only accounts for the pi-orbitals. The computed results clearly include the methylene group in the HOMO-1 and the olefin protons in the LUMO+1.
Part b) Hydrogenation of dicyclopentadiene:

Cyclopentadiene contains two olefin groups. One resides in the boat shaped cyclohexene ring (can also be described as being cyclopentene ring with the bridging group) and the other in the side cyclopentene ring. Hydrogenation of the cyclohexene ring will result in only the boat conformer of cyclohexane forming. This is a result of the bridging group, which is 1,3-disubstituted, exerting a steric lock on the ring. As previously mentioned this olefin is also in a cyclopentene ring, hydrogenation forms the stable 'envelope' structure (where four carbons lie in a plane and the final carbon lie above the plane) that is present in free cyclopentane (possibly a source of stabilisation). Hydrogenation of the cyclopentene ring will form the same 'envelope' structure, although on comparison to the other cyclopentane ring, the extent to which this happens is far less. MM2 optimisation of these structures rendered the following results:
| Energy Type | Hydrogenation of cyclopentene ring (Energy kcal/mol) | Hydrogenation of cyclohexene ring (Energy kcal/mol) |
|---|---|---|
| Jmol pop-up | ||
| Stretch | 1.2349 | 1.0965 |
| Bend | 18.9383 | 14.5244 |
| Stretch-Bend | -0.7609 | -0.5494 |
| Torsion | 12.1242 | 12.4974 |
| Non-1,4 VDW | -1.5018 | -1.0701 |
| 1,4 VDW | 5.7289 | 4.5126 |
| Dipole/Dipole | 0.1631 | 0.1406 |
| Total Energy | 35.9266 | 31.1520 |
The results in Table 21b1T indicate that the hydrogenation of the cyclohexene ring gives the lower energy system. Thus it is the thermodynamic product. Considering the change in computed energy (E (endo-dicyclopentadiene) = 34kcal/mol) across the reaction it is clear that hydrogenation of the alkene of the cyclopentene ring results in a raising of the energy (endothermic) and the hydrogenation of the alkene in the cyclohexene ring results in a lowering of the free energy (exothermic). This would infer that the transition state of the cyclopentene hydrogenation system will resemble the products and the cyclohexene hydrogenation system will resemble the reactants by Hammond’s Postulate. Excluding the alkene consider nothing else changing in the system. The alkene system being hydrogenated is either in a constrained six membered ring or a five membered ring. The difference in energy is largely accounted for by the bending contribution. The bending energy describes the ability of the molecules to move (bend) about is equilibrium bonding structure. The energy is calculated using equations based on Hooke's Law. This means that hydrogenation of the cyclohexene ring results in a bonding structure which can fluctuate about flexible positions with greater ease. This can therefore infer two properties of the molecules, it is more rigid (steric lock on cyclohexane and olefin in cyclopentene restrict movement and hence less natural bending) and position that can bend will bend with a lower force constant, i.e. the bond is more flexible for a given energy. Consideration of the product structures leads to the conclusion that rigidity is the major factor that makes the cyclohexene hydrogenation product more stable.
Stereochemistry of nucleophilic additions to a pyridinium ring (NAD+ analogue)
Part a) Grignard Reagents[2]
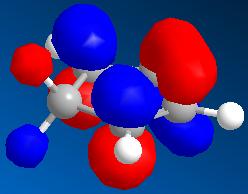
Optimisation of the NAD+ derivative results in a structure where the carbonyl group (C=O) lies above (or below) the plane of the pyridine ring (± 41.9°, Figure 22a1F). The product of Grignard addition is expected to have a methyl group eclipsed with the carbonyl.
| Energy kcal/mol | |
|---|---|
| Stretch | 0.9232 |
| Bend | 6.6122 |
| Stretch-Bend | 0.1252 |
| Torsion | 9.4514 |
| Non-1,4 VDW | -2.4898 |
| 1,4 VDW | 11.5762 |
| Charge/Dipole | 3.2887 |
| Dipole/Dipole | -3.7781 |
| Total Energy | 25.7090 |
Grignard reagents provide a source of carbanions which attack electron deficient centres. They are usually made by reaction of magnesium with alkyl-halide. Various modification can be made to the reagent to control its reactivity such as addition of copper which makes the reagent softer and will cause the Grignard to favour a 1,4-Michael addition over a 1,2-carbonyl addition in an α,β-unsaturated ketone. It is common to find reactions of Grignards with carbonyl and olefins in literature due to the ease of reagent production and the reactivity of the carbanions towards these functionalities. In this reaction MeMgI added to an NAD+ analogue forming a methyl adduct on the 4-position of the pyridine ring. Grignard attack is controlled by the hard-hard soft-soft type reactivity where hard nucleophiles attack hard regions of positive charge, similarly for soft nucleophiles which attack soft positive centres. If the Grignard was MeMgBr the anticipated result would be attack at the carbonyl, but the change of halide has an effect on the nucleophile making it softer. As a result 1,4-addition is observed (as previously described with Cu Grignard's).
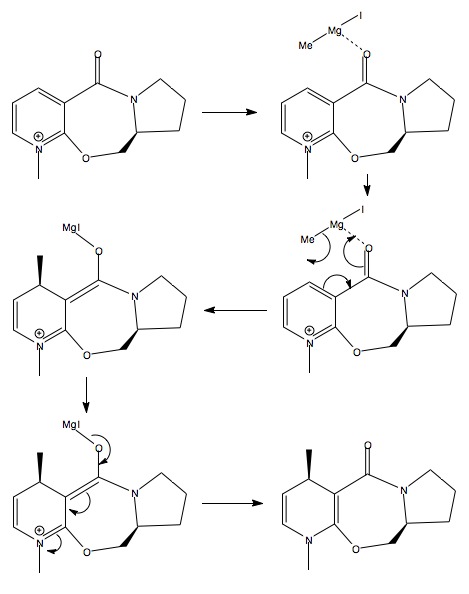
The stereochemistry of the resulting methyl adduct is somewhat unusual. Consider the initial structure (provided as an interactive Jmol (above)), the carbonyl can be observed to be above the plane of the pyridine ring (41.9°)(Figure 22a1F, below) along with the ether (predefined stereochemistry). If the carbanion attacked as a free anion the expectation would be for attack from below the plane of the pyridine ring and therefore avoiding the electron rich oxygen. This would result in the opposite stereochemistry to that which is observed. This means there must be another factor controlling the stereochemistry. Consider that the reaction passes by via a chelation mechanism, this would be able to hold the carbanion in position to attack from the same side of the ring as the oxygen, via a concerted mechanism, Scheme 22a1S (above), forming the enolate anion and metal halide cation. The carbonyl can then reform and pass the negative charge to the nitrogen thus forming a neutral species.

|
|
When trying to optimise the structure the Grignard was added with the reactant to see what happened. An error occurred when MeMgI was added, but when Me- was added it unsurprisingly sat below the positive nitrogen in line with the empty pz orbital of said nitrogen.
Part b) Nucleophiles (Amines)[3]
In this experiment a more complex NAD+ molecule was investigated. The molecule consists of four rings systems, three of which are aromatic and hence planar. The seven membered ring (the only ring which is not aromatic) is left free to adopt conformations to minimise the energy of the molecule. Optimisation methods were run on layouts which were analogous to the chair (near planar) and boat conformations of cyclohexane. The chair-like conformation where ~200kcal/mol compared to ~15kcal/mol for the boat-like conformer. This is a substantial difference of energy, rendering the chair-like very unstable. The majority of this instability arises from bend energy (65%). The carbonyl was calculated to lie at an angle of 44.5°.
| Energy kcal/mol | |
|---|---|
| Stretch | 1.5217 |
| Bend | 6.3297 |
| Stretch-Bend | 0.3274 |
| Torsion | -5.9309 |
| Non-1,4 VDW | -2.7030 |
| 1,4 VDW | 17.6018 |
| Charge/Dipole | 2.4518 |
| Dipole/Dipole | -4.7913 |
| Total Energy | 14.8073 |
|
|
It is then suggested that the NAD+ analogue will undergo nucleophilic attack at the 4-position on the pyridine ring. The stereochemistry of the products indicates that the nitrogen nucleophile will attach on the same face as the methyl (predefined stereochemistry). The reaction is determined to be 1,4 addition to an α,β-unsaturated ketone as for the Grignard example above. However, in this case there is no chelation control so the expectation would be for a racemic mixture to form. It could be suggested that attack from the same face as the carbonyl may be disfavoured due to repulsion of the two highly negative species. Attack from the other face could also be disfavoured due to the methyl group interfering the attack trajectory. From these arguments it is impossible to determine which isomer will be formed in excess, there must be another effect which causes the selectivity.
| Energy kcal/mol | |
|---|---|
| Stretch | 2.6914 |
| Bend | 62.0433 |
| Stretch-Bend | -1.2256 |
| Torsion | -28.9724 |
| Non-1,4 VDW | -7.0053 |
| 1,4 VDW | 17.2087 |
| Dipole/Dipole | -6.4418 |
| Total Energy | 38.2983 |
The Nuclear Overhauser Effect (NOE) is the factor which controls the addition. There is significant stabilisation due dipolar coupling between the methyl group attached to the chiral carbon in the lactam ring and the hydrogen of the amine nucleophile. This can only occur if both the methyl and the amine are on the same sides of the rings. Optimisation of this structure is complicated, values between 300 and -15kcal/mol where achieved. Negative steric energy is not feasible and analysis of these structures indicates significant deformation of the benzene ring, to the point where p-orbital overlap would be minimal and aromaticity would be lost. The best positive energy achieved was 38.3kcal/mol using MM2 optimisation. The calculated dipole-dipole energy was -6.44kcal/mol, this is a stabilisation (-ve), and is evidence of the NOE. Optimisation analysis of most of the molecules in this project has returned dipole-dipole interactions approximately equal to zero, hence stabilisation of this product is significant and can is fully accounted for by the NOE.
Total Synthesis of Taxol[4]
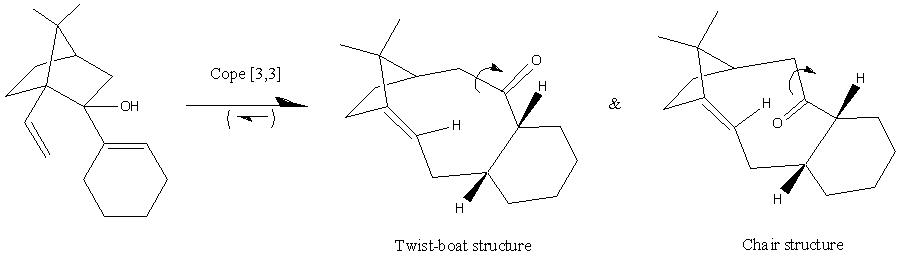
The norbornane derivative in the total synthesis of taxol (Scheme 231S, above) can undergo an oxy-cope rearrangement. This will form an enol which will rapidly tautomerise to the carbonyl (C=O stronger, and hence more stable, than C=C). This molecule can adopt two conformations in the saturated ring, either a chair or twist-boat. Geometric optimisation (MM2) of both conformers shows that the twist-boat conformer is the more stable by ~15kcal/mol, Table 231T. The difference in energy is largely accounted for by bending energy.
| Energy Type | Twist-boat conformer Energy kcal/mol | Chair conformer Energy kcal/mol |
|---|---|---|
| Jmol pop-up | ||
| Stretch | 2.5462 | 3.2007 |
| Bend | 10.6616 | 20.2891 |
| Stretch-Bend | 0.3196 | 0.4898 |
| Torsion | 19.6972 | 21.8994 |
| Non-1,4 VDW | -1.3231 | -0.5978 |
| 1,4 VDW | 12.5449 | 14.4400 |
| Dipole/Dipole | -0.1813 | -0.0002 |
| Total Energy | 44.2651 | 59.7209 |
The alkene in the resulting oxy-Cope rearrangement can be described as hyperstable.
Definition (according to Maier & von Ragué Schleyer)[5]:
[A "hyperstable" olefin is one which contains] less strain than that of the parent hydrocarbon and have negative OS values [(OS = strain energy of olefin - strain energy of parent hydrocarbon)]. Such olefin should be very unreactive-not due to steric hinderance or to enhanced π-bond strength but due to special stability afforded by the cage structure of the olefin and to the greater strain of the parent poly cycloalkane.[
The hyperstability (by definition) of these olefins can be shown by calculating the OS energy. Optimisation (MM2) of the hydrogenated olefins gave an energy of 57.97kcal/mol for the twist-boat conformer and 60.00kcal/mol for the chair conformer. The resulting OS values are -13.7kcal/mol for the twist-boat and -0.28kcal/mol for the chair conformer. The twist-boat olefin is very stable relative to the hydrogenated product, however the chair is only just less strained so it would not be expected to be as unreactive as the twist-boat.
| Energy Type | Twist-boat hydrogenation product Energy kcal/mol | Chair hydrogenation product Energy kcal/mol |
|---|---|---|
| Jmol pop-up | ||
| Stretch | 3.0853 | 3.4155 |
| Bend | 16.553 | 19.2018 |
| Stretch-Bend | 0.6524 | 0.5851 |
| Torsion | 22.3613 | 21.2476 |
| Non-1,4 VDW | 0.0814 | 0.4403 |
| 1,4 VDW | 15.2365 | 15.4091 |
| Dipole/Dipole | 0.0000 | 0.0000 |
| Total Energy | 57.9722 | 60.2993 |
A more general explanation can be shown by comparing the energy changes for the hydrogenation of the taxol intermediate and ethene. For the taxol intermediate, both hydrogenation products have a higher ground state energy than the corresponding olefins, therefore the process is an endothermic in both cases. Now consider ethene, standard enthalpy data of ethene, ethane and hydrogen (all measured at standard temperature and pressure) results in a enthalpy change of -32.7kcal/mol for hydrogenation of ethene. Thus hydrogenation is exothermic for this process. By Hammond's postulate the stabilisation of the products makes the transition state move towards the reactants, and if the transition state is nearer the reactants it is more exothermic. The hydrogenation of the taxol intermediate is proposed to be a endothermic process and hence the transition state is towards the product side of the reaction coordinate. As a result, the 'activation energy' or energy barrier would be expected to be higher hence the term 'hyperstable alkene'.
Peptide Hydrolysis[6]
It is possible for some peptides to under an intramolecular hydrolysis reaction cleaving the amide forming ammonia and an ester containing ring. In this example there is a large difference of rates between two isomers. Molecular mechanics (MM2) has been employed to investigate the structures to try to ascertain an explanation for this behaviour. The peptides in question are based on a cis or trans decalin like ring structure and are therefore relatively rigid about said rings. There is one key variation that can occur in each isomer, this is the amide positioning. The nitrogen in the ring can allow a equatorial or an axial amide to form. The orientation of the ring (cis or trans) then allows for a further set differences. It is this that ultimately controls the rate of hydrolysis.
Part a) cis-decalin isomer
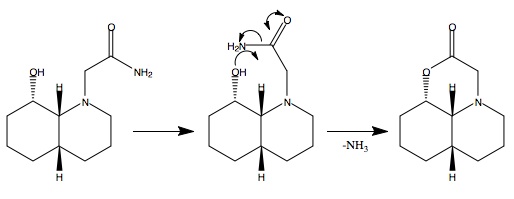
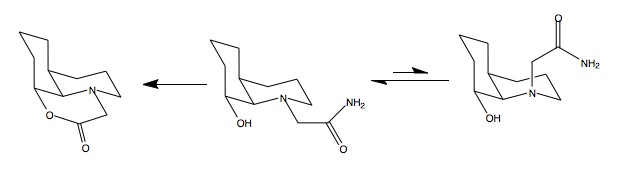
Geometric optimisation (MM2) of the two possible conformers results in energies of 15.99kcal/mol for the equatorial and 19.31kcal/mol for the axial conformer. These results indicate that the equatorial isomer is more stable by 3.3kcal/mol so this isomer would be expected to dominate in the equilibrium of conformers, Figure 241F (below). For hydrolysis to occur it is required that the hydroxyl group be in the vicinity of the carbonyl. This is only the case in the equatorial conformer, Figure 241F. As this conformer dominates the equilibrium, the reaction is expected to proceed with a relatively high rate as the reaction is promoted by equilibrium.
| Jmol pop-up |
|---|
Details of two conformers:
| Energy Type | Axial Conformer Energy kcal/mol | Equatorial Conformer Energy kcal/mol |
|---|---|---|
| Stretch | 1.4893 | 1.4595 |
| Bend | 5.3690 | 8.2178 |
| Stretch-Bend | 0.5857 | 0.6701 |
| Torsion | 10.3165 | 9.4044 |
| Non-1,4 VDW | -4.4797 | -6.6667 |
| 1,4 VDW | 9.5566 | 9.4220 |
| Dipole/Dipole | -3.5237 | -6.5186 |
| Total Energy | 19.3137 | 15.9884 |
There is significant stabilisation from dipole-dipole and Non-1,4 VDW interactions (approximately 6kcal/mol per interaction) in the equatorial conformer compared to the axial. All other parameter are roughly equal except bending energy which is increased in the equatorial isomer (cancelled by stabilising dipole-dipole and Non-1,4 VDW). This probably arises due to interactions of the amide with the ring system causing higher energy bending. Analysis of the H-bonding type interactions in the equatorial conformer identifies that the labile OH proton is eclipsed with the oxygen lone pairs on the carbonyl (interaction shown below in Figure 242F), whilst the acidic alpha-proton of the carbonyl is eclipsed with the lone pair of the oxygen in the alcohol group. Initial result showed values as high as 177kcal/mol, with most of the energy arising from bending. These structures did not have the carbonyl H-bonding interactions and there where obvious alterations (such as moving the amide group) which lowered the energy of the system.
Part b) trans-decalin isomer
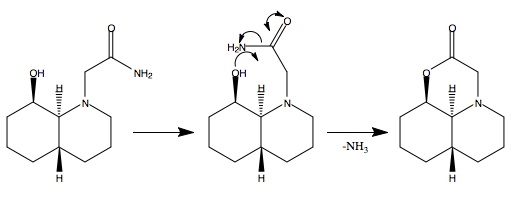
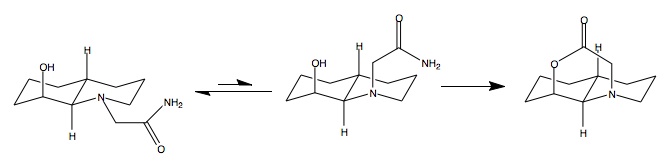
The amide can adopt two conformation as before, either equatorial or axial, Scheme 243S (below). MM2 results produce a total energy of 11.99kcal/mol for the axial isomer and 9.65kcal/mol for the equatorial. As the two conformations are in equilibrium with each other it is plausible to suggest that the equatorial isomer will dominate the axial isomer because it is more stable. With regard to hydrolysis, Scheme 242S (above), only one of the two conformers has the correct functional group positioning for the reaction to proceed, Scheme 243S. In this case it is the axial isomer. As previously determined the axial isomer is the minor conformer in equilibrium so cannot react as fast as with the previous example because the formation of the reacting conformer is controlled under equilibrium.
| Jmol pop-up |
|---|
Details of two conformers:
| Energy Type | Axial Conformer Energy kcal/mol | Equatorial Conformer Energy kcal/mol |
|---|---|---|
| Stretch | 1.5301 | 1.4609 |
| Bend | 5.1171 | 3.7502 |
| Stretch-Bend | 0.5498 | 0.5018 |
| Torsion | 8.7288 | 7.7953 |
| Non-1,4 VDW | -7.0782 | -7.3139 |
| 1,4 VDW | 9.6194 | 9.9324 |
| Dipole/Dipole | -6.4796 | -6.4766 |
| Total Energy | 11.9874 | 9.6501 |
The only significant difference between isomers is the bending energy, which is less in the axial conformer. The difference will arise purely as a result of the position of the amide. In the axial conformer the amide is open space rather than in line with the ring where it can interact with the other atoms, this could lead to easier atom movement and hence a lower bending energy about equilibrium positions. As before, with the previous peptide there is significant stabilisation by dipole/dipole interactions. Looking at the Jmol pop-ups, labile proton of the alcohol can be seen to interact with the carbonyl thus forming said dipole/dipole interaction. This can happen in both conformers with almost exactly the same stabilisation. With regard to hydrolysis, as previously mentioned only the axial can be attacked by the hydroxyl group, this can be observed by looking at the Jmol pop-ups, the equatorial amide and the alcohol will not get close enough to attack, thus hindering the reaction.
Conclusions
Both isomers are observed to undergo intramolecular hydrolysis in relative short time scales. In small molecule chemistry, the expectation is that the amide is more stable than the product ester and the amide will therefore resist attack and not hydrolyse. The reason why the two above peptides undergo such rapid hydroylsis is due to the nature of the reaction, intramolecular and ring forming. The activation barrier for the process is lowered because the product can be stabilised by a new ring structure (5-membered) and the reaction can proceed faster as the reaction kinetics will be first order with respect to the reactant as the reaction is unimolecular and requires no diffusion.
Semi-Empirical Molecular Orbital Theory
Regioselective addition of dichlorocarbene to 9-chIoro-1,4,5,8-tetrahydro-4a,8a-methanonaphthaIene[7]
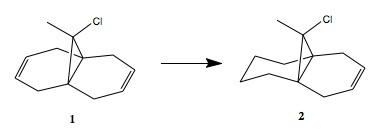
MM2
| Energy Type | 1 kcal/mol | 2 kcal/mol |
|---|---|---|
| Jmol pop-up | ||
| Stretch | 0.6186 | 0.9014 |
| Bend | 4.6637 | 4.6767 |
| Stretch-Bend | 0.0385 | 0.0131 |
| Torsion | 7.7183 | 10.7567 |
| Non-1,4 VDW | -1.0721 | -1.0708 |
| 1,4 VDW | 5.8209 | 6.9962 |
| Dipole/Dipole | 0.1127 | 0.0704 |
| Total Energy | 17.9006 | 22.3437 |
Guassian Molecular Orbitals (Frontier Orbital Region)(HF/STO-3G)
Classical versus Quantum Mechanics:
In all these examples the dihedral angle between the cyclopropane ring and the olefin. The smaller the angle, the closer the olefin is to the cyclopropane ring. The exo-alkene is defined to be the alkene on the opposite side to the chlorine and the endo-alkene is defined to be the alkene on the same side as the chlorine.
Analysis of 1:
MM2 optimises based on classical mechanics, based on coulombic interactions of various types (e.g. Van der Waals). The results of optimisation produce a structure would have C2 symmetry if the Cl was replaced by H, depicted in Table 313.2T (below). HF/STO-3G is a quantum mechanical calculation (with a poor basis set, STO-3G), the results show deviation from the MM2 optimisation. The exo-alkene is now closer to the cyclopropane ring than the endo-alkene, the dihedral angle were measured to be 62° and 42° respectively. The results of the second quantum mechanical optimisation (B3LYP/6-31G(d), better basis set than before) show a clear indication of endo-alkene movement towards the cyclopropane ring, the dihedrals in this case were 68° for the exo-alkene and 49° for the endo-alkene. It also be observed that the B3LYP/6-31G(d) result places the olefin and the C-Cl bond in the same plane.
| MM2 | HF/STO-3G | B3LYP/6-31G(d) |
|---|---|---|

|

|
|
These observations can be justified by considering what is causing the movement. As previously mentioned the olefin is in the same plane as the C-Cl bond. Increasing complexity leads to this result (more complex, more accurate) so it is likely that there is some interaction causing stabilisation between this olefin and the C-Cl. It turns out that the stabilisation is a result of a overlap of the olefin π-molecular orbital and the C-Cl σ* orbital. Excluding this interaction one might expect that the two olefins would have a degenerate HOMO (as both the HOMO and HOMO-1 are based on the pi-bonds of each orbital, Table 313.1T (above)). The C-Cl σ* orbital is found at LUMO+2, Figure 313F (below), and will mix with the HOMO to form a more stable exo-alkene HOMO-1 (thus removing degeneracy), Table 313.1T (above).
Analysis of 2:
The MM2 results show a structure with a twisted cyclohexane ring (twist-boat) due to the steric lock of the cyclopropane and cyclohexene adducts 1,2 on the ring. Optimisation with HF/STO-3G and B3LYP/6-31G(d) does not affect the ring structure significantly.
Conclusions:
As a result is can be proven that the C-Cl σ* overlap with C=C is the key source of stabilisation as it is not observed when the said C=C is hydrogenated. In terms of the reactivity of 9-chIoro-1,4,5,8-tetrahydro-4a,8a-methanonaphthaIene (by considering MOs in Table X) the expectation is that the endo-alkene will behave like a nucleophile as there is high orbital (and hence electron) density in the C=C π-orbital in the HOMO. Whereas the exo-alkene will behave as an electrophile due to the high orbital density on the C=C π-orbital in the LUMO.
IR analysis
B3LYP/6-31G(d) of 1
The optimisation results for the 1 produced an IR spectrum with five intense peaks. These are tabled below in Table 314T, an assignment for the origin of the stretch or bend has been made.
| Frequency / Hz | 690 | 770 | 3010 | 3030 | 3180 |
|---|---|---|---|---|---|
| Wavelength / μm | 2.30 | 2.57 | 10.0 | 10.1 | 10.6 |
| Assignment (S = stretch, B =bend) | CH (B) | CH (B) & CCl (S) | CH (S)(methylene) | CH (S)(methylene) | CH (S)(olefin) |
The olefin stretching produces substantially less intensity. The endo-alkene has a stretching frequency of 1760.91cm-1 and the exo-alkene has a stretching frequency of 1740.76cm-1. The major C-Cl stretch is at 772.62cm-1.
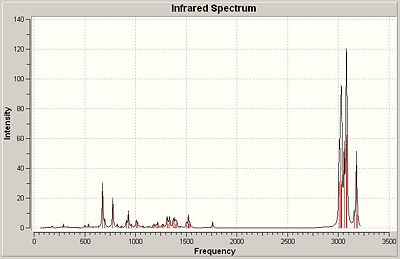
B3LYP/6-31G(d) of 2
The mono-hydrogenation product produces a infra red spectrum with lots of low intensity peaks in the 600-1500 range. All of these can be attributed to bending modes, most of the hydrocarbon system rather than the chlorine. The C=C stretch appears at 1761.68cm-1. The high intensity peaks are C-H stretches, the lower end (around 3000cm-1) result from methylene proton stretches. The olefin proton stretches appears at 3155-3177cm-1. The C-Cl stretch appeared at 777cm-1.
| Dialkene 1 | Monohydrogenated alkene 2 |
|---|---|
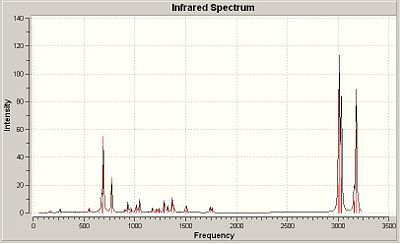
|
|
Conclusions & Observations:
The two olefin groups in 1 have different stretching frequencies indicating different bond strengths (by Hooke's Law, frequency proportional to the root of bond strength). Thus the exo-alkene (20 wavenumbers lower) has a weaker bond than the endo-alkene. This is concurrent with previous observation as the decrease in bond strength can be accounted for by mixing with σ* C-Cl and thus lowering the pi-bond order and hence strength. Comparison of the two C-Cl stretching frequencies of 1 and 2 indicates a weaker bond in 1 (4.38 wavenumbers shorter). This, again, supports previous conclusions because if mixing where to occur between the alkene and the antibonding orbital of C-Cl then the would be electron density in the antibonding orbital to some degree. This will reduce bond order (BO=(N(B)-N(AB))/2, N(B) = no. of bonding electrons, N(AB) = no. of antibonding electrons) and hence the bond strength will decrease.
DFT-based Mini Project
Part a) Investigation of "Click Chemistry" (Course Defined)[8]
Background
"Click Chemistry" is a type of Chemistry defined by Sharpless. It refers to reactions which are fast and reliable, hence "click". This investigation centres on a 1,3 dipolar cycloaddition reaction with an azide and an alkyne, Scheme 411S (below)

It is known that the 1,3-substituted product is favoured by Cu(I) catalysts and the 1,2-substituted product is favoured by Ru(II) catalysts.
Aims
The aim of this investigation is to compute the carbon 13 NMR of the products and compare to literature data.
Literature Data
1,2-substituted product 13C NMR (CDCl3): δ 51.85, 126.93, 127.22, 128.22, 128.92, 129.08, 129.64, 133.26, 133.34, 135.66, 138.26.
Computed Data
1,2-substitution:

| Jmol |
|---|
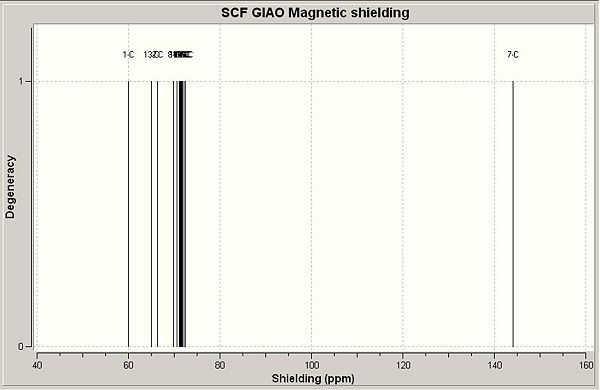
13C NMR (CDCl3) δ 60.1 (4), 65.1 (7), 66.4 (3), 69.9 (14/9, away from other ring), 70.6 (16), 71.1 (15/17, away from other ring), 71.3 (15/17, nearest other ring), 71.4 (8), 71.5 (10/12, away from other ring), 71.6 (9/13, nearest other ring), 71.7 (9/13, away from other ring), 71.8 (14/18, nearest other ring), 72.1 (11), 72.5 (10/12, nearest other ring), 144.1 (6).
1,3-substitution:
| Jmol |
|---|
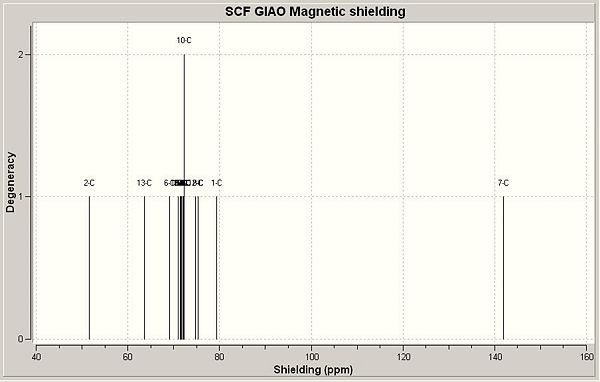
13C NMR (CDCl3) δ 51.6 (6), 63.6 (8), 69.1 (6), 71.0 (12, on N side w.r.t. N-ring), 71.3 (15, on N side w.r.t. N-ring), 71.5 (17, on C side w.r.t. N-ring), 71.6 (11), 71.7 (10, on C side w.r.t. N-ring), 71.9 (9, on C side w.r.t. N-ring), 72.2 (13, on N side w.r.t. N-ring), 72.2 (16), 74.7 (14, on N side w.r.t. N-ring), 75.3 (18, on C side w.r.t. N-ring), 79.4 (4), 141.9 (7).
Analysis
The literature results show fewer peaks than for the computed data. This is because the computed data does not take into account degeneracy of the system, more a picture at 0K where every carbon is distinguishable. The peaks separation is also very different, for example the high field peak in the computed data is not observed in the literature. Although the carbon to which is relates would seem to be stabilised rather than destabilised because it is adjacent to an aromatic ring.
Conclusions
This experiment aimed to reproduce the carbon 13 NMR of the two products. On comparison to the literature it is clear that the quantum mechanics cannot take into account motion of the molecule and thus the peaks are distorted between the sets. One suggestion for this could be peak averaging causing the differences. With regard to the highly shifted peak at ~140ppm, it could be assumed it was to shifted too far to be recorded.
It must also be noted that when optimising with MM2 initially the molecule tended to twist and warp the aromaticity leading to negative steric energies so MOPAC optimisation was employed to resolve this issue, and this was the basis for the original Guassian Input File.
Part b) Investigation of intermediates in the synthesis of conformationally restricted nicotine analogues by intramolecular [3+2] cycloaddition [9] (Own Research)
Background
It is known that nicotine targets and activates nicotinic acetylcholine receptors (nAChRs) in the brain. These receptors play a part in the processes which lead to nervous system disorders such as Alzheimer's, Parkinson's and Tourette's. It is thought that development of constrained nicotine analogues could lead to blocking of the nAChRs sites and thus hindering the processes which lead to the before mentioned diseases.
Aims
The aim of this modelling experiment is to investigate a ring closure process in the total synthesis of cis-1-methyl-1,2,3,3a,4,8b-hexahydropyrrolo[3,2-f]-pyrindine. The key steps are provided below, Scheme 421S.

The addition of sarcosine creates two isomers, depending on whether the MOMO protecting group is on the same side as the labelled hydrogens (up) or on the opposite side (down), Scheme 422S (below). Ultimately, the formation of isomers does not effect the end product as MOMO protecting group is removed and the alcohol removed. However, the paper provides detailed analysis of the two isomers so it is possible to compare DFT methods with this data.

Literature Data
Reported 1.37:1 ratio of MOMO down:MOMO up.
MOMO up (same side as stereo-defined H's):
13C NMR (CDCl3, 75MHz) δ 24.2, 41.8 46.0, 55.8, 57.2, 71.6, 77.9, 96.4, 120.3, 138.1, 147.0, 148.8, 151.4.
MOMO down (opposite side to stereo-defined H's):
13C NMR (CDCl3, 75MHz) δ 24.1, 41.7, 45.8, 55.7, 57.1, 71.4, 77.8, 96.3, 120.2, 138.0, 146.8, 148.6, 151.3
Computed Data
Jmol's:
MOMO up derivative

MM2:
| Energy kcal/mol | |
|---|---|
| Stretch | 1.6768 |
| Bend | 14.0139 |
| Stretch-Bend | 0.4561 |
| Torsion | 9.7284 |
| Non-1,4 VDW | -2.47190 |
| 1,4 VDW | 13.8280 |
| Dipole/Dipole | 1.6363 |
| Total Energy | 38.6205 |
NMR results:
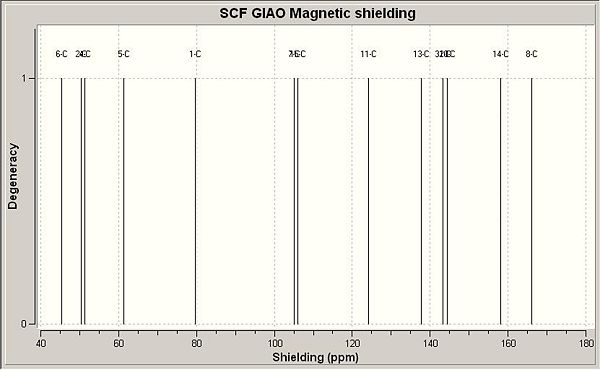
13C NMR (CDCl3) δ 46.2 (6), 51.3 (2), 52.8 (4), 64.9 (5), 79.1 (1), 99.2 (18), 118.2 (9), 126.4 (7), 144.0 (20), 145.1 (11), 150.0 (8), 159.6 (17), 172.35 (12).
IR results:

νmax/cm-1 (pure) 1035.35 (C-N), 1135.19 (C-O), 1176.36 (C-O), 1183.45 (C-O), 1624.18 and 1647.12 (C=N), 1647.12 (C=C aromatic), 2948.59 (C-H, S, 17), 3002.96 (C-H, S, 20), 3015.16 (C-H, S, 18). More generally, around the 1000Hz area are C-H bending modes except for those indicated above which relate to specific vibrations. 3000Hz region relates to C-H stretching frequency with various modes.
MOMO down derivative
MM2:
| Energy kcal/mol | |
|---|---|
| Stretch | 1.4173 |
| Bend | 12.4415 |
| Stretch-Bend | 0.2309 |
| Torsion | 10.7567 |
| Non-1,4 VDW | -3.9531 |
| 1,4 VDW | 14.0507 |
| Dipole/Dipole | 2.8031 |
| Total Energy | 37.7471 |
NMR results:
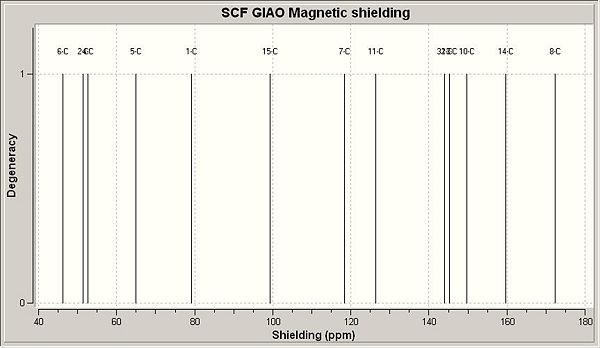
13C NMR (CDCl3) δ 46.3 (6), 51.4 (2), 52.7 (4), 64.9 (5), 79.2 (1), 99.2 (18), 118.3 (9), 126.5 (7), 144.1 (20), 145.2 (11), 149.7 (8), 159.6 (17), 172.3 (12).
IR results:
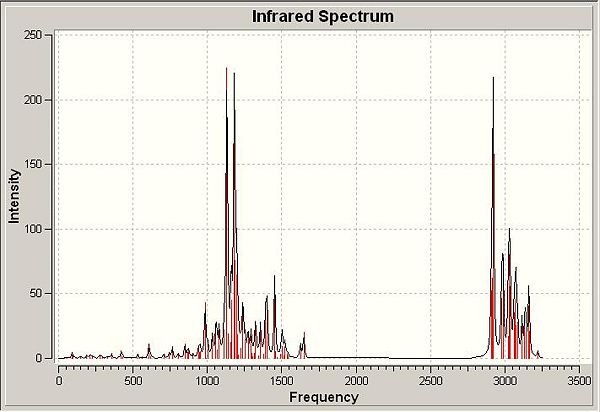
νmax/cm-1 (pure) 1057.91 (C-N), 1130.8 (C-O), 1179.45 (C-O), 1185.67 (C-O), 1625.95 and 1648.13 (C=N), 1648.13 (C=C aromatic), 2921.86 (C-H, S, 17), 2996.9 (C-H, S, 20), 3027.02 (C-H, S, 18). As before, peaks around the 1000Hz area are C-H bending modes except for those indicated above which relate to specific vibrations. 3000Hz region relates to C-H stretching frequency with various modes.
Analysis
The literature provides a carbon NMR but no assignments. Using the MPW1PW91/6-31(d,p) method it has been possible to optimise the molecule and then compute an NMR for each isomer. The results do not match number for number however the peak seperated for computed and literature is approximately equal which suggests there is just an issue with NMR references. The computed results have provided a spectrum from which the environments can be assigned. Comparing MOMO up and MOMO down isomers of both computed and literature it is clear there is very little difference between isomers and the changes that do occur (usually about 0.1ppm) are in the same direction for literature and computed. The opportunity was taken to run IR analysis of the molecules, although none was provided in the literature. The results show the expected stretches for C=N, C-O etc. This merely confirms that the optimisation method used has produced a molecule which reflects the equilibrium structure in the real world. With regard to ratios of the isomers produced in the reaction with sarcosine it was stated in the literature a 1.37:1 ratio of MOMO up:MOMO down. MM2 optimisation shows that the MOMO down derivative is more stable by ~0.9kcal/mol. Thus the MOMO down is the thermodynamic product and hence the reaction must be under thermodynamic control, i.e. equilibrium control.
Conclusions
The intention of this investigation was to assign the environments of the carbon NMR in the literature. This has been achieved although the expectation was for better differentiation between the two isomer but unfortunately the two isomer are in fact very similar in terms of carbon environments. The proton environment could be analysed but the results show no splitting so it would fairly pointless the most important data from a proton NMR comes from the splitting. The ratio of product has been accounted for by simply MM2 calculation and the reaction type determined as result. In all the exercise was a success but proton NMR analysis would improve upon the results found.
References
- ↑ N. J. Turro, G. S. Hammond, J. Am. Chem. Soc., 1962, 84 (14), pp 2841–2842
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chem., 1986, 51, 838
- ↑ S. Leleu, C. Papamicael, F. Marsais, G. Dupas, V. Levacher, Tetrahedron: Asymm., 2004, 15, 3919-3928
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319
- ↑ W. F. Maier, P. v. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891
- ↑ M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, J. Org. Chem., 2008, 73, 6413–6416
- ↑ B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc.,Perkin Trans. 2, 1992, 447.
- ↑ L. Zhang, X. Chen, P. Xue, H. H. Y. Sun, I. D. Williams, K. B. Sharpless, V. V. Fokin and G. Jia, J. Am. Chem. Soc., 2005, 127 (46),15998–15999
- ↑ X. Yang, S. Luo, F. Fang, P. Liu, Y. Lu, M. He and H. Zhai, Tetrahedron, 2006, 62, 2240