Rep:Mod:jh6415 TS

Introduction

In this lab, it was aimed to find and identify the transition states for a series of Diels-Alder reactions, using the program Gaussian. Transition states occur on a potential energy surface, where the potential energy surface maps the potential energy of the system as a function of the relative coordinates of the participating atoms, generating a multi-dimensional surface, with the involved molecules possessing 3N_atoms-6 geometric variables. The reaction coordinate can be described as a function of these 3N_atoms-6 internal coordinates. The transition state is a stationary point on the surface; a point which has a zero gradient, a first derivative equal to zero and where all forces vanish:

$\frac{\mathrm{d}E(\mathbf{R})}{\mathrm{d}{R}_i}=0i=1,2,...,3N_{\mathbf{a}\mathbf{t}\mathbf{o}\mathbf{m}\mathbf{s}}-6$

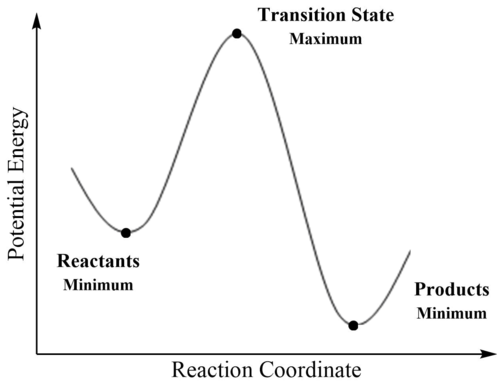
where R corresponds to all nuclear coordinates and R_i to a specific nuclear coordinate. Stationary points include both minima and maxima, hence we look at the second derivative of a stationary point, which is related to the curvature of the surface, in order to correctly classify it. The second derivative of the potential energy is equal to the force constant. A minimum corresponds to the point where any form of displacement in any direction results in an increase in energy of the system, and hence has a positive second derivative. The reaction coordinate joins two energy minima, with the maximum in energy between these two points corresponding to the transition state, where the second derivative is negative. Since the transition state is characterised as the energy maximum, it represents an energy barrier that must be overcome for the reaction to proceed. The difference in energies between stationary points allows calculation of activation and reaction energies: the activation energy corresponds to the energy difference between the transition state maximum and the reactant minimum and is related to the reaction kinetics, whilst the reaction energy is the difference between the reactant and product minima and concerns thermochemical properties, such as equilibrium.^1,2 The simplified relationship between these stationary points is displayed below in figure 1.

Nf710 (talk) 17:31, 22 February 2018 (UTC) You haven't described the stationary points in the 3N-6 degrees of freedom. the second derivatives for each normal modes are the eigenvalues of the hessian matrix and the normal modes are the eigenvectors which are a linear combination of the degrees of freedom.

Figure 1. Potential energy curve displaying the simplified relationship between the reactants, products and their transition state.

Location of the transition structures was carried out with Gaussian, using one of three possible methods. The first and simplest involves essentially guessing the structure of the transition state and although the quickest, it is also the most unreliable method, requiring knowledge of the transition state structure, so somewhat limits the application of this method. The reliability of this method is extended in the second method, by freezing the atoms involved in bonding in the transition state and minimising the structure before optimisation. However, the transition state still needs to be known. Whilst the third method is the longest, it is also the most reliable, and hence was the preferred method for the following exercises. It involves beginning from either optimised reactants or products, then altering the structure to resemble the transition state before optimisation.

In Gaussian, two different calculation methods were used: PM6 and B3LYP. PM6 is a semi-empirical method and B3LYP is a density functional theory (DFT) method, which used a 6-31(d) basis set. PM6 is based on the Hartree-Fock formalism and is a non-ab initio method (not from first principles). Instead, the PM6 method uses ab initio reference data, such as thermochemistry and molecular geometries, and a series of assumptions and parameter optimisations in its calculations, resulting in a faster computational method.³ On the other hand, B3LYP is a hybrid functional which incorporates ab initio features (such as from Hartree-Fock methods) into DFT methods, and uses a basis set. The basis set is a series of functions utilised in DFT methods to act as the electronic wave function, consisting of atomic orbitals which linearly combine to form molecular orbitals. When calculated with Gaussian, the transition state possesses a single negative vibration, which corresponds to an imaginary frequency, as a result of the force constant being negative for the transition state.

Nf710 (talk) 17:32, 22 February 2018 (UTC) You have shown some good understanding here. It would have been nice to have some equations to back up the theory you are talking about.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Excellent work across this section - great job!)

In this exercise, the transition state for the Diels-Alder reaction between ethene and butadiene was identified, then the molecular orbitals for the optimised reactants and transition state were visualised, in order to construct an MO diagram. The reaction coordinate was also illustrated through analysis of the changing bond lengths and animation of the transition state vibration and IRC.

Reaction Scheme

Figure 2. Reaction scheme for the Diels-Alder reaction between butadiene and ethene.

MO Diagram for the Formation of the Transition State

An MO diagram was constructed for the Diels-Alder reaction, as displayed in figure 3, where the HOMO and LUMO of ethene combined with the respective HOMO and LUMO of butadiene. In figure 3, we see that the symmetric HOMO of ethene, the lowest energy MO of the four frontier MOs, combines with the symmetric LUMO of butadiene, generating the symmetric HOMO and LUMO of the transition state. The new MOs are both higher in energy than ethene's HOMO but lower in energy than butadiene's LUMO. The antisymmetric LUMO of ethene combines with the antisymmetric HOMO of butadiene, resulting in another two antisymmetric MOs - the HOMO -1 and LUMO +1 of the transition state. Again, these new MOs are higher in energy than the reactant HOMO but lower in energy than the reactant LUMO. The newly formed transition state MOs have a greater contribution from whichever original MO they are closer in energy to.

Figure 3. MO diagram for the transition state formation for the Diels-Alder reaction between butadiene and ethene.

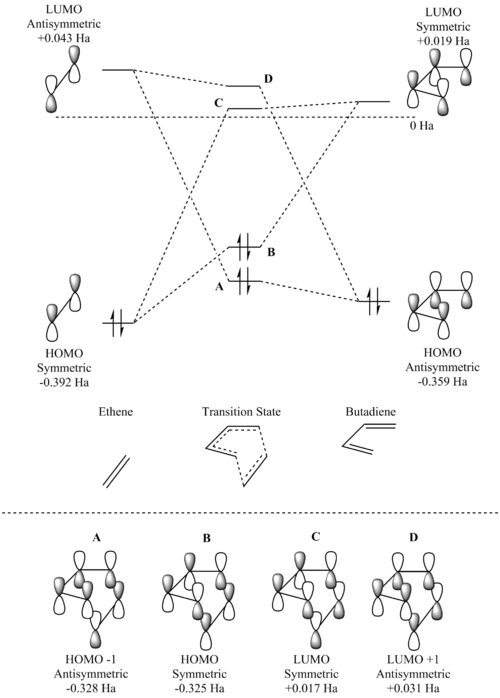
From figure 3, we can see that there is a symmetry requirement in order for the orbitals to overlap. Both orbitals must be of the same symmetry for an allowed interaction, whilst an interaction between MOs of different symmetry is forbidden. Therefore, the orbital overlap integral will take a non-zero value for symmetric-symmetric and antisymmetric-antisymmetric interactions, but will be equal to zero for a symmetric-antisymmetric interaction, and hence explains the observed HOMO-LUMO orbital interactions between ethene and butadiene.

Usually, when two MOs combine, the two new MOs that are generated consist of a bonding MO that is lower in energy than the original two MOs, and an antibonding MO that is higher in energy. However, it is important to note that the MO diagram is for the formation of the transition state, not the product, hence the new bonds have not been entirely formed. The transition state is always higher in energy than the products as it occurs at the maximum in potential energy.

HOMO & LUMO of Reactants and Transition State

The molecular orbitals of the reactants (ethene and butadiene) were visualised and are displayed in table 1, along with the four molecular orbitals of the transition state that the reactants' HOMO and LUMOs combine to form. The MOs in table 1 can be correlated to those displayed in the MO diagram in figure 3. From table 1, we can see that the ethene HOMO and the butadiene LUMO are symmetric, whilst the ethene LUMO and the butadiene HOMO are antisymmetric. From looking at the transition state HOMO -1, we can see that this MO is antisymmetric and was generated from a bonding interaction between the ethene LUMO and butadiene HOMO, whilst the antisymmetric LUMO +1 is the result of the antibonding interaction. Likewise, the symmetric TS HOMO is from the bonding interaction between the ethene HOMO and butadiene LUMO, and the TS LUMO from the antibonding interaction.

Table 1. The molecular orbitals of the reactant HOMO/LUMOs and the resulting transition state molecular orbitals.

Reactants
Ethene HOMO	Ethene LUMO	Butadiene HOMO	Butadiene LUMO
Transition State
Transition State HOMO -1	Transition State HOMO	Transition State LUMO	Transition State LUMO +1

Bond Lengths of Reactants, Transition State and Products

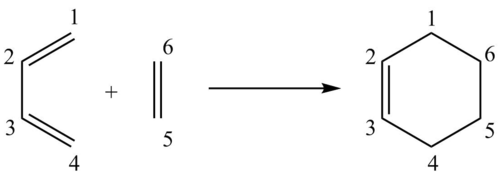
The carbon-carbon bond lengths were observed to change during the course of the reaction as the reactants formed first the transition state, and then the products. The change in bond length is due to the change in carbon hybridisation. In figure 4, as shown below, the respective carbons have been labelled to indicate the bond lengths that are referred to in table 2.

Figure 4. Labelled reaction scheme for the Diels-Alder reaction.

Table 2. Carbon-carbon bond lengths in the reactants (ethene and butadiene), transition state and product (cyclohexene).

C-C Bond	C-C Bond Length (Å)
	Reactants		Transition State	Product
	Ethene	Butadiene		Cyclohexene
C1-C2	-	1.333	1.380	1.501
C2-C3	-	1.471	1.411	1.337
C3-C4	-	1.333	1.380	1.501
C4-C5	-	-	2.114	1.537
C5-C6	1.328	-	1.382	1.535
C6-C1	-	-	2.115	1.537

From table 2, it can be seen that the double bonds of butadiene (C1-C2 and C3-C4) increase in length from 1.333 Å to 1.380 Å in the transition state, then to 1.501 Å in the product. The double bond of ethene (C5-C6) similarly increases in length, as a result of the carbon hybridisation changing from sp² to sp³, giving a reduction in s character. The hybridisation of the C1 and C4 atoms also changes from sp² to sp³, with the double bonds in the reactants becoming single bonds in the product, as a result of the [4+2] cycloaddition, so the distance between the nuclei increases due to fewer bonding electrons. The butadiene single bond (C2-C3) decreases from 1.471 Å to 1.411 Å, then 1.337 Å in the product, although the carbon atoms do not change hybridisation, but remain sp². The distance between the carbon atoms however shortens to maximise the overlap of the p orbitals to form the double bond.

Two new bonds are formed in the reaction (between C4-C5 and C1-C6), and these distances shorten on going from the transition state to the product as the single bonds are formed. In the cyclohexene product, the C1-C2 and C3-C4 single bonds (1.501 Å) are found to be shorter than the other single bonds in the molecule, since one of the two bonding carbons has remained sp² hybridised, giving a greater s character to the bond. These two particular single bonds are also shorter than literature values for typical sp³-sp³ C-C bonds (1.543 Å), whilst the other single bonds in the product agree to two decimal places. All double bonds are in agreement with a literature value of 1.333 Å.⁴ The partly formed C-C bonds in the transition state (C4-C5 and C1-C6) have a length of 2.114/2.115 Å, which can be compared to the Van der Waals radius of the carbon atom, which is 1.700 Å.⁵ The partly formed C-C bonds therefore have a shorter length than the sum of two Van der Waals radii (3.400 Å), indicating a bonding interaction between the carbons in the transition state as a bond begins to form.

The bond lengths of the transition state can be seen to be closer to that of the reactants than the products. This suggests that the transition state resembles the reactants more closely than the products, and following the Hammond postulate, the transition state is closer in energy to the reactants and hence formed early. This indicates that this particular Diels-Alder reaction is exothermic, which could have been confirmed by comparing the reactant and product energies.

Reaction Path Vibration of Transition State

The above Jmol object illustrates the vibration representing the reaction path from the transition state, and is the transition state vibration that occurs at an imaginary frequency. It can be seen that the formation of both C-C single bonds is synchronous, since the Diels-Alder reaction is a concerted process. This can also be observed in the IRC, as shown below, where it can be seen that the two single bonds are formed at the same time.

Figure 5. IRC for the Diels-Alder reaction between butadiene and ethene. Click to animate if necessary.

Log Files

• PM6 Optimised Reactant - Ethene = File:Jh6415 ETHENE OPTIMISATION PM6.LOG
• PM6 Optimised Reactant - Butadiene = File:Jh6415 BUTADIENE OPTIMISATION PM6.LOG
• PM6 Optimised Transition State = File:Jh6415 DA REACTION TS OPTI PM6.LOG
• Transition State IRC = File:Jh6415 DA REACTION IRC PM6 TRY 2.LOG
• PM6 Optimised Product - Cyclohexene = File:Jh6415 PRODUCT OPTIMISED ATTEMPT 2.LOG

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

In this exercise, the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole was investigated. The transition states for both the endo and the exo reactions were identified and MO diagrams were constructed for both of the cycloadditions, with the relevant MOs once again visualised. The activation and reaction energies were additionally calculated and compared for the endo and exo reactions. Finally, the secondary orbital interactions and steric effects were also explored.

Reaction Scheme

Figure 6. Reaction scheme for the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole.

Nf710 (talk) 17:43, 22 February 2018 (UTC) Why must they be the same energy for them to overlap. There is an equation.

MO Diagram for the Formation of the Endo/Exo Transition States

(Fv611 (talk) Very nice MO diagrams, and well done on pointing out that the conformations have different TS MO energies. You could have pushed it further and attempted a guess at why that might be!)

MO diagrams were constructed for both the endo and exo transition state formations, with the difference in the transition states related to the approach of the 1,3-dioxole towards the diene: in the exo transition state, the ring oxygens of the dienophile are positioned away from the diene, while in the endo transition state, the oxygens lie underneath the diene, as can be seen in table 3. The effect of this will be discussed in further detail below. As in exercise 1, the frontier MOs must have the same symmetry in order to overlap, with this symmetry requirement governing the interactions observed in the below MO diagrams. The same MOs interact in both the endo and exo reactions, although the generated transition state MOs have different energies.

Table 3. The MO diagrams for the endo/exo Diels-Alder reactions between cyclohexadiene and 1,3-dioxole.

Endo Diels-Alder	Exo Diels-Alder

In a normal electron demand Diels-Alder reaction, the HOMO of the diene interacts with the LUMO of the dienophile to generate the transition state HOMO and LUMO, whereas in an inverse electron demand Diels-Alder reaction, it is the LUMO of the diene that interacts with the dienophile HOMO. This is because in the normal electron demand reaction, the diene often possesses an electron donating substituent and hence is electron rich, while the dienophile possesses an electron withdrawing substituent and is electron deficient. On the other hand, this is reversed for the inverse electron demand reaction, and the dienophile is raised in energy due to its electron-rich nature, such that the dienophile HOMO now lies above the diene HOMO, hence it is now the dienophile HOMO that interacts, as this is closest in energy to the diene LUMO. From table 3, it is evident that both the endo and exo Diels-Alder reactions are inverse electron demand, since it is the HOMO of 1,3-dioxole that interacts with the LUMO of cyclohexadiene to generate the transition state HOMO and LUMO. The reason for this is that 1,3-dioxole is an electron rich dienophile due to the electron donating nature of the ring oxygens, so the 1,3-dioxole HOMO is raised in energy above the cyclohexadiene HOMO, and interacts more strongly with the cyclohexadiene LUMO, since it is closer in energy.

On comparison of the two MO diagrams, it can be seen that the HOMO -1, the LUMO and the LUMO +1 of the endo transition state all lie higher in energy than the respective MOs of the exo transition state. Additionally, the LUMO +1 is destabilised by a greater amount than the HOMO -1 and the LUMO. On the contrary, the HOMO of the endo transition state is lower in energy and hence more stabilised than the HOMO of the exo transition state. The reasons for these observations will be discussed in the below section, where the secondary orbital interactions are visualised and considered.

Nf710 (talk) 17:45, 22 February 2018 (UTC) You can test this quantitatively by doing a single point energy calculation on the reatants in the irc.

HOMO & LUMO of Reactants and Endo/Exo Transition States

The HOMO and LUMOs of the reactants, along with the four MOs they generate in both the endo and exo transition states are displayed in table 4 below. The symmetric MOs are as follows: the 1,3-dioxole HOMO, cyclohexadiene LUMO and the HOMO and LUMO of the transition states. Therefore, the antisymmetric MOs are the 1,3-dioxole LUMO, cyclohexadiene HOMO and the HOMO -1 and LUMO +1 of the transition states.

Table 4. The molecular orbitals of the reactant HOMO/LUMOs and the resulting transition state molecular orbitals.

Reactants
1,3-Dioxole HOMO	1,3-Dioxole LUMO	Cyclohexadiene HOMO	Cyclohexadiene LUMO
Endo Transition State
Endo Transition State HOMO -1	Endo Transition State HOMO	Endo Transition State LUMO	Endo Transition State LUMO +1
Exo Transition State
Exo Transition State HOMO -1	Exo Transition State HOMO	Exo Transition State LUMO	Exo Transition State LUMO +1

Activation and Reaction Energies

The activation and reaction energies for each reaction pathway were calculated from the energy difference between the Gibbs free energy of the transition state and the reactants, and the energy difference between the Gibbs free energy of the products and reactants, respectively. The calculated energies are displayed in table 5.

Table 5. Gibbs free energies of reactants, transition states and products and the resulting activation energy and reaction energy for the endo/exo Diels-Alder reactions between cyclohexadiene and 1,3-dioxole.

Reaction Type	Energy (kJ/mol)
	Reactants			Transition State	Product	Activation Energy	Reaction Energy
	Cyclohexadiene	1,3-Dioxole	Total
Endo	-612593.20	-701188.77	-1313781.97	-1313622.16	-1313849.38	159.81	-67.41
Exo				-1313614.32	-1313845.74	167.65	-63.77

From table 5, we can see that the exo transition state is higher in energy than the endo transition state, which results in a greater activation energy for the exo Diels-Alder reaction. In the exo reaction, the reactants must gain a greater amount of energy in order to overcome the activation barrier, and so the endo product is the kinetic product. We can therefore infer that the endo transition state is more stabilised than the exo transition state. Upon comparing the reaction energies, we see that both processes are exothermic, and hence thermodynamically favourable. The endo product is however lower in energy than the exo product, hence both the endo transition state and product are more stabilised. This results in a more negative reaction energy for the endo reaction and a consequently more exothermic process, so the endo product is also the thermodynamic product.

Secondary Orbital Interactions & Steric Effect

As previously described, the endo reaction is both the kinetically and thermodynamically favoured pathway, due to both the endo transition state and product being more stabilised, as a result of a secondary, non-bonding orbital interaction. As can be seen in table 6 below, in the HOMO of the endo transition state, the ring oxygens of 1,3-dioxole are able to interact with the butadiene orbitals, since the oxygen p orbitals have the correct phase and alignment to overlap with the orbitals of the butadiene molecule. This results in the stabilisation of the endo transition state. No such interaction is possible in the exo transition state HOMO, since the 1,3-dioxole molecule is positioned differently, such that the ring oxygens are orientated away from the diene, so orbital interactions are purely primary. The endo product is also more stable, which can be explained in terms of sterics. Looking back at the reaction scheme in figure 6, we can see that in the endo product, the newly fused dioxole ring is orientated away from the bridging carbons, avoiding any steric clash, whereas in the exo product, the dioxole ring is orientated towards the bridging carbons, giving an energetically unfavourable steric effect. This results in the exo product lying higher in energy.

Table 6. The secondary orbital interactions and steric effects in the endo and exo transition states.

Endo HOMO	Exo HOMO

Nf710 (talk) 17:51, 22 February 2018 (UTC) This was a good section very nicely formatted. Your energies are correct and you have come to the correct conclusions.

Log Files

• B3LYP Optimised Reactant - Cyclohexadiene = File:Jh6415 CYCLOHEXADIENE OPTIMISED B3LYP.LOG
• B3LYP Optimised Reactant - 1,3-Dioxole = File:Jh6415 DIOXOLE OPTIMISED B3LYP ATTEMPT 2.LOG
• B3LYP Optimised Endo Transition State = File:Jh6415 ENDO TS OPTI TS B3LYP.LOG
• B3LYP Optimised Exo Transition State = File:Jh6415 EXO TS OPTI TS B3LYP.LOG
• Endo Transition State IRC = File:Jh6415 ENDO TS IRC PM6 (CORRECT DIRECTION).LOG
• Exo Transition State IRC = File:Jh6415 EXO TS IRC.LOG
• B3LYP Optimised Endo Product = File:Jh6415 ENDO PRODUCT OPTIMISED B3LYP.LOG
• B3LYP Optimised Exo Product = File:Jh6415 EXO PRODUCT OPTIMISED B3LYP.LOG

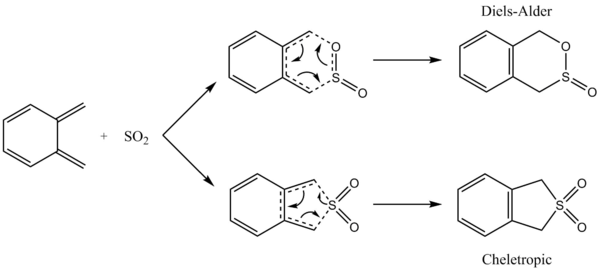
Exercise 3: Diels-Alder vs Cheletropic

In this exercise, the reaction between xylylene and sulphur dioxide was investigated, and the endo and exo Diels-Alder transition states, along with the cheletropic transition state were located. Each possible reaction pathway was visualised by animation of the IRC. The reaction and activation energies for each pathway were calculated to find the kinetically and thermodynamically favoured pathways, and to generate a reaction profile. An alternate Diels-Alder reaction was additionally explored.

Reaction Scheme

Figure 7. Reaction scheme for the Diels-Alder and cheletropic reaction between xylylene and sulphur dioxide.

Visualisation of Reaction Coordinate

An IRC calculation was performed for each pathway and has been animated in the table below. In the endo Diels-Alder reaction, the sulphur dioxide molecule approaches the diene with one of its oxygens orientated towards the diene, whereas in the exo Diels-Alder reaction, the oxygen is orientated away from the diene. In both of the Diels-Alder reactions, the diene bonds to the oxygen before the sulphur, so the bond forming process is asynchronous here. In the cheletropic reaction, it can be seen that the reactants no longer undergo a [4+2] cycloaddition, but instead both new bonds are formed to the sulphur atom. These bonds are formed at the same time, so this bond forming process is synchronous. Xylylene is a highly unstable molecule, and from observation of the IRCs in table 7, we see that in all three reactions, the aromatic 6-membered ring is generated before new bonds are formed with sulphur dioxide. Therefore, xylylene is unstable, since product formation will be heavily favoured due to the large stabilisation of the product as a result of its aromaticity.

Table 7. The IRCs for the cheletropic and endo/exo Diels-Alder reactions between xylylene and sulphur dioxide. Click to animate if necessary.

Cheletropic	Endo Diels-Alder	Exo Diels-Alder

Activation and Reaction Energies

As in exercise 2, the activation and reaction energies were calculated for each possible reaction pathway, and the results are displayed below in table 8. The cheletropic transition state is the highest energy of the three reactions, thus the cheletropic reaction has the highest activation energy. The endo Diels-Alder transition state is the lowest energy. Therefore, the endo Diels-Alder pathway is the most kinetically favoured as it has the lowest activation energy. Looking at the products, the endo Diels-Alder product is the highest in energy (although it is very similar in energy to the exo product), and the cheletropic product is the lowest in energy. The reaction energies show that all three reactions are exothermic, but the cheletropic reaction has the most negative reaction energy, so is the most exothermic. Therefore, the cheletropic reaction is the thermodynamically favoured product.

Table 8. Gibbs free energies of reactants, transition states and products and the resulting activation energy and reaction energy for the cheletropic and endo/exo Diels-Alder reactions between xylylene and sulphur dioxide.

Reaction Type	Energy (kJ/mol)
	Reactants			Transition State	Product	Activation Energy	Reaction Energy
	Xylylene	Sulphur Dioxide	Total
Cheletropic	467.42	-311.42	156.00	260.09	0	104.09	-156.00
Endo				237.77	56.97	81.77	-99.03
Exo				241.75	56.38	85.75	-99.67

The calculated activation and reaction energies were used to create the reaction profile as shown in figure 8, displaying the relative energies of the transition states and the products for each pathway. The endo Diels-Alder transition state is the lowest energy, since it is stabilised by a secondary orbital interaction of the oxygen p orbital of sulphur dioxide with the diene π orbitals. Such an interaction is not possible in the exo Diels-Alder and cheletropic reactions. The cheletropic transition state is the highest energy, since the formation of the five-membered ring in the transition state is more strained than when the six-membered ring is generated in the Diels-Alder transition state. The endo and exo Diels-Alder products are very similar in energy, but the cheletropic product is much more stabilised, as it contains an extra S=O double bond.

Figure 8. Reaction profile for the Diels-Alder and cheletropic reactions between xylylene and sulphur dioxide.

Alternate Diels-Alder Reaction

An alternate Diels-Alder reaction is also possible between the reactants, since xylylene contains another cis-butadiene fragment that can undergo [4+2] cycloaddition, with the Diels-Alder reaction occuring between sulphur dioxide and the diene inside the ring in xylylene, as can be seen in the IRCs in table 9.

Table 9. The IRCs for the alternate endo/exo Diels-Alder reactions between xylylene and sulphur dioxide. Click to animate if necessary.

Endo Diels-Alder	Exo Diels-Alder

From table 10, it can be seen that the endo pathway has a lower activation energy than the exo, and this is due to stabilisation of the transition state by the previously discussed secondary orbital interactions. The endo pathway also has a less positive reaction energy, so the endo product is both the kinetic and thermodynamic product. However, if we compare the activation energy values in table 10 to those of the other Diels-Alder reaction in table 8, we can see that both reactions have a larger activation barrier for the alternate Diels-Alder reaction, and are hence more kinetically unfavourable. The reactions are also thermodynamically unfavourable, since the products are higher energy than the reactants, resulting in an endothermic reaction with a positive reaction energy. This is because there is no aromaticity generated in the product, as was the case with the normal Diels-Alder reaction.

Table 10. Gibbs free energies of reactants, transition states and products and the resulting activation energy and reaction energy for the alternate endo/exo Diels-Alder reactions between xylylene and sulphur dioxide.

Reaction Type	Energy (kJ/mol)
	Reactants			Transition State	Product	Activation Energy	Reaction Energy
	Xylylene	Sulphur Dioxide	Total
Endo	467.42	-311.42	156.00	267.98	172.26	111.99	16.26
Exo				275.82	176.71	119.82	20.71

Log Files

• PM6 Optimised Reactant - Sulphur Dioxide = File:Jh6415 SO2 REACTANT OPTIMISED PM6.LOG
• PM6 Optimised Reactant - Xylylene = File:Jh6415 XYLYLENE REACTANT OPTIMISED PM6.LOG
• PM6 Optimised Cheletropic Transition State = File:Jh6415 CHELETROPIC TS PM6 TS.LOG
• PM6 Optimised Endo Diels-Alder Transition State = File:Jh6415 ENDO DA TS PM6 TS.LOG
• PM6 Optimised Exo Diels-Alder Transition State = File:Jh6415 EXO DA TS PM6 TS.LOG
• Cheletropic Transition State IRC = File:Jh6415 CHELETROPIC TS PM6 IRC.LOG
• Endo Diels-Alder Transition State IRC = File:Jh6415 ENDO DA TS PM6 IRC.LOG
• Exo Diels-Alder Transition State IRC = File:Jh6415 EXO DA TS PM6 IRC.LOG
• PM6 Optimised Cheletropic Product = File:Jh6415 CHELETROPIC PRODUCT PM6 OPTIMISED.LOG
• PM6 Optimised Endo Diels-Alder Product = File:Jh6415 ENDO DA PRODUCT PM6 OPTIMISED.LOG
• PM6 Optimised Exo Diels-Alder Product = File:Jh6415 EXO DA PRODUCT PM6 OPTIMISED.LOG
• PM6 Optimised Alternate Endo Diels-Alder Transition State = File:Jh6415 ALTERNATE DA ENDO TS PM6 TS.LOG
• PM6 Optimised Alternate Exo Diels-Alder Transition State = File:Jh6415 ALTERNATE DA EXO TS PM6 TS.LOG
• Alternate Endo Diels-Alder Transition State IRC = File:Jh6415 ALTERNATE DA ENDO TS PM6 IRC.LOG
• Alternate Exo Diels-Alder Transition State IRC = File:Jh6415 ALTERNATE DA EXO TS PM6 IRC.LOG
• PM6 Optimised Alternate Endo Diels-Alder Product = File:Jh6415 ALTERNATE DA ENDO PRODUCT OPTIMISED PM6.LOG
• PM6 Optimised Alternate Exo Diels-Alder Product = File:Jh6415 ALTERNATE DA EXO PRODUCT OPTIMISED PM6.LOG

Further Work: Electrocyclic Ring Opening

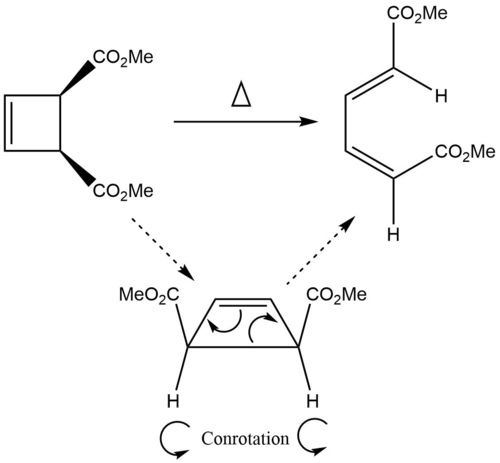
In this further work, the transition state for an electrocyclic ring opening reaction was located and optimised, along with the reactant and product. The IRC was calculated and visualised, then the MOs of the reactant, transition state and product were analysed to explain the observed conrotation of the reaction.

Reaction Scheme

Figure 9. Reaction scheme and mechanism for the electrocyclic ring opening reaction.

Visualisation of Reaction Coordinate

The IRC for the electrocyclic ring opening reaction was animated, as can be seen in figure 10. The thermally driven reaction proceeds via conrotation. From the IRC, we can see that a single bond is broken and a new double bond is formed, as shown in the mechanism in figure 9. It can also be seen that both of the ester groups rotate in the same direction, generating the observed stereochemistry in the product.

Figure 10. IRC for the electrocyclic ring opening reaction. Click to animate if necessary.

HOMO & LUMO of Reactant, Transition State and Product

The HOMO and LUMO of the reactant, transition state and product were visualised for the reaction and are displayed in table 11. The conrotation observed in the reaction can be explained via Woodward-Hoffmann analysis. The 4π electrocyclic reaction has one antarafacial component, and is thus thermally allowed. Looking at the product MOs, we can see that in the reverse ring closing reaction, the diene termini must rotate in the same direction in order for an in-phase interaction between the orbitals to occur, which can indeed be observed in the transition state MOs. The same process is apparent in the ring opening reaction, resulting in conrotation.

Table 11. The molecular orbitals of the reactant, transition state and product.

Reactant
HOMO	LUMO
Transition State
HOMO	LUMO
Product
HOMO	LUMO

(MO analysis of this system is far more complicated than it seems initially. It's clear that in the closure reaction, the bonding interaction in the HOMO upon conrotation drives the reaction forwards, but what is less clear is how those MOs evolve. Mobius aromaticity greatly complicates the process by allowing pi orbitals to switch phase and change overall symmetry of the MO Tam10 (talk) 11:51, 26 February 2018 (UTC))

Log Files

• PM6 Optimised Reactant = File:Jh6415 ELECTROCYCLIC REACTANT OPTIMISED.LOG
• PM6 Optimised Transition State = File:Jh6415 ELECTROCYCLIC TS PM6 OPT TS.LOG
• Transition State IRC = File:Jh6415 ELECTROCYCLIC TS PM6 IRC.LOG
• PM6 Optimised Product = File:Jh6415 ELECTROCYCLIC PRODUCT OPTIMISED.LOG

Conclusion

The transition states for a plethora of Diels-Alder reactions were successfully located and characterised using PM6 and B3LYP calculation methods in Gaussian. Method 3 was the preferred method for the exercises. In exercise 1, via MO analysis, a symmetry requirement for orbital combination was identified and bond formation was found to be synchronous. In exercise 2, both the endo and exo Diels-Alder reactions were identified as inverse electron demand due to the raised energy of the electron rich dienophile HOMO. The endo reaction was identified as the kinetic and thermodynamic pathway, due to stabilisation of the transition state by a secondary orbital interaction, and a reduced steric clash in the product. In exercise 3, the endo Diels-Alder pathway was the kinetic reaction, whereas the cheletropic pathway was the thermodynamic reaction. An alternate Diels-Alder reaction was also possible, but was both kinetically and thermodynamically disfavoured. Finally, in the further work, the thermal electrocyclic ring opening reaction was identified to proceed via conrotation.

References

1. J. J. W. McDouall, Computational Quantum Chemistry: Molecular Structure and Properties in Silico, The Royal Society of Chemistry, Cambridge, 2013, pp. 1-62.
2. D. J. Wales, Energy Landscapes, Cambridge University Press, Cambridge, 2003, pp 1-5.
3. J. J. Stewart, J. Mol. Model., 2007, 13, 1173-1213.
4. D. R. Lide Jr, Tetrahedron, 1962, 17, 125-134.
5. S. S. Batsanov, Inorg. Mater., 2001, 37, 871-885.