Physical Computational Module 3

In this computational experiment, GaussView was used to model reactions.

There are 5 parts in this experiment:

Part one: Optimization of the reactant / product for 1,5-hexadiene Cope Rearrangement.

Part two: Transition State modelling method 1. Chair conformation was guessed as transition state geometry for Cope Rearrangement Reaction. Calculation was conducted to verify the geometry.

Part three: Transition State modelling method 2. The reactant and product of Cope Rearrangement Reaction were drawn out; QST2 method was used to approaching the transition state geometry. Boat Conformation was the transition state geometry.

Part four: Use the transition modelling methods in part 2 and 3 for butadiene and ethylene reaction (Diels-alder reaction). Use the energies and orbitals calculated to predict the mechanism.

Part five: Extend the understanding of part four and apply it to cyclohexa-1,3-diene and maleic anhydride reaction.

PART 1 Optimization of Reactant/Product for 1,5-hexadiene Cope Rearrangement

In this part, optimizing reactant/product and transition state structures, calculating vibrational frequency and correcting potential energy were done. The activation energy can then be calculated in order to compare with the experimental data.

The Cope rearrangement was developed by Arthur Cope and the mechanism is [3,3] sigmatropic reaction. During the reaction, one C-C σ bond breaks and one σ forms. The generally accepted idea is that the reaction is via chair or boat transition state. The energy of the boat transition state is higher than the one of chair transition state. [1]

An'anti' and a 'gauche' like conformers are drawn manually, and then they were optimized. The two conformers were distorted to the minimum energy structure. The resultant energy can then be calculated and compared. It has been found out that the 'Anti' structure has lower energy.

Conformer

Structure

Point Group

Energy/Hartrees
HF/3-21G

Compare to Appendix A [2]

Anti

Anti

C₂

-231.6926

anti 1

Gauche

Gauche

C₂

-231.6915

gauche 4

PART 2 Transition State Modelling Method 1 (Chair Conformation of Cope Rearrangement)

There are two ways to approach the transition state of the reaction. For Chair conformation, the guessed transition structure was drawn out and was optimized to minimum energy. For Boat conformation, the reactant and the product were drawn out, a method called QST2 was used to help locating the transition state.

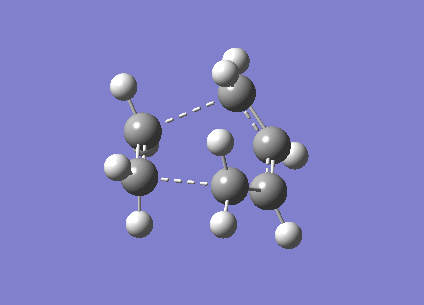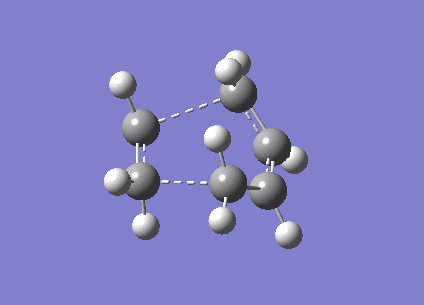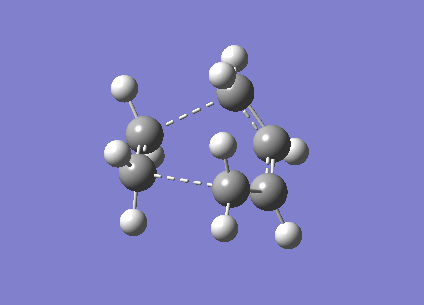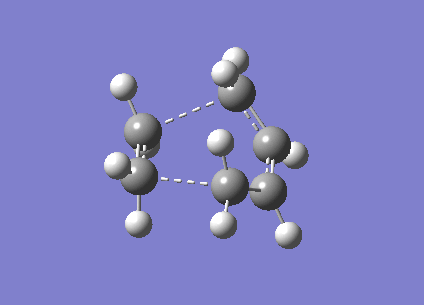
The guessed transition state of chair conformation consists of two fragments which are 2.20Å apart. The guessed transition state can be optimized by two different methods: Optimization to TS(Berny)and Bond freezing.

Optimization to TS(Berny)

Bond Length

Energy (Hartrees)

Structure

Animation

Frequency

Chair TS

C₃C₁₄ =2.02017

C₆C₁₁ =2.02015

TS1

-231.61932

The imaginary frequency calculated by the first method is -817.86nm.

Bond Freezing

Bond Length

Energy (Hartrees)

Structure

Chair TS

C₃C₁₄ =2.02069

C₆C₁₁ =2.02050

TS1

-231.61932

As shown in the two tables above, the two methods give similar outcomes.

PART 3 Transition State Modelling Method 2 (Boat Conformation of Cope Rearrangement)

The anti2 conformer that refers in Appendix A can be considered as reactant and the different types of energies can be calculated.

HF/3-21G

Electronic energy (Hartrees)

Sum of electronic and zero-point energies(Hartrees) at 0K

Sum of electronic and thermal energies at(Hartrees) 298.15K

the sum of electronic and thermal enthalpies(Hartrees)

the sum of electronic and thermal free energies(Hartrees)

Structure

Anti2 (C_i) Reactant

-231.69254

-231.53954

-231.53257

-231.46040
H = E + RT

-231.49521
G = H - TS

ci

B3LYP/6-31G*

Electronic energy(Hartrees)

Sum of electronic and zero-point energies(Hartrees) at 0K

Sum of electronic and thermal energies(Hartrees) at 298.15K

the sum of electronic and thermal enthalpies(Hartrees)

the sum of electronic and thermal free energies(Hartrees)

Structure

Anti2 (C_i) Reactant

-234.61171

-234.46920
E = E_elec + ZPE

-234.46186
E= E+E_vib + E_rota +E_trans

-234.46091
H = E + RT

-234.50078
G = H - TS

ci'

The vibrational frequencies of the reactant (anti2) are all positive which suggested that it is not a transition state but a stable structure.

The optimization method for Boat Transition State is called QST2. Transition State can be located by calculation after reactant and product were specified. The calculation will fail if the reactant and the product were not similar to the transition state, e.g. the following graph.

The reactant and product needed to be distorted as followed in order to give correct transition state.

Intrinsic Reaction Coordinate

By using the Intrinsic Reaction Coordinate, the minimum energy pathway from transition state to potential energy surface of the reaction is shown. The pathway is divided into a number of points and each point coordinates to a small geometry change. From Intrinsic Reaction Coordinate, the energy of the transition state and the product or reactant can be easily obtained.

For the chair conformation above, the transition state geometry was guessed. By using Intrinsic reaction coordinate, the structure of transition state can be verified. The energies of the transition state and the product or reactant can be calculated as well.

Results Table

	HF/3-21G			B3LP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Chair TS (Hartrees)	-231.61932	-231.46670	-231.46134	-234.55698	-234.41492	-234.40900
*Reactant (Gauche 3) (Hartrees)*	-231.692535	-231.539539	-231.532566	-231.61932	-231.46670	-231.46134
Activation Energy in kcal/mol		at 0K 45.70	at 298.15K 44.69		at 0K 34.06	at 298.15K 33.17

	HF/3-21G			B3LP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Boat TS(Hartrees)	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39601
*Reactant (Gauche 3)(Hartrees)*	-231.69253	-231.53954	-231.53257	-234.61171	-234.46920	-234.4619
Activation Energy in kcal/mol		at 0K 55.60	at 298.15K 54.76		at 0K 41.32	at 298.15K 41.32

The activation energy can be calculated by substrating reactant energy by transition state energy. The conversion of Hartrees to kcal: 1 hartree=627.509kcal/mol.

The experimental activation energies for chair and boat conformations at 0K are 33.5±0.5 kcal/mol and 44.7±2.0 kcal/mol respectively, which are closer to the data obtained from the B3LYP/6-31G* method. This implies B3LYP method has higher level calculation.

Also, as the transition state energy of chair conformation is lower than the boat conformation, the chair conformation transition state would be the dominant one.

PART 4 Butadiene and Ethylene Reaction (Diels-Alder Cycloaddition)

There are four ways for locating the transition structure and its energy. The first one is drawing out the guessed transition state and use HF method to optimize it. The second one is similar but using 63G method. The third one is QST2 method, the detailed process is same to the boat transition state locating above; HF calculation method was used. The forth one is similar to the third one but using 63G calculation method.

The table below shows the bond length, transition state energy and HOMO/LUMO images for each of the four method listed above.

	Optimization TS (Benry)			QST2 Method
	Structure of TS (Hartrees)	Energy of TS (Hartrees)	Bond Length (Å)	Structure of TS (Hartrees)	Energy of TS (Hartrees)	Bond Length (Å)
HF Method		-231.60321	C₂-C₆=2.2090 C₁-C₃=2.2099		-234.54390	C₂-C₆=2.2724 C₁-C₃=2.2722
B3LYP/6-31G*		-231.60321	C₁-C₇=2.2096 C₄-C₁₀=2.2092		-234.54390	C₁-C₃=2.1193 C₂-C₆=2.1193
Semi/AM1		0.11165	C₁-C₇=2.2096 C₄-C₁₀=2.2092		0.11165	C₁-C₇=2.1202 C₄-C₁₀=2.1184

When same level of calculation method was used, the results are the same for using both TS(Benary) and QST method. The two lengths of the forming bonds are the same which suggested it is a synchronous reaction.

The HOMO,LUMO of the reactants and the transition states are shown below.

	HOMO	LUMO	Discussion
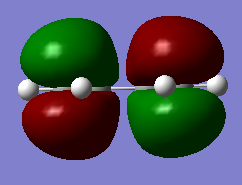
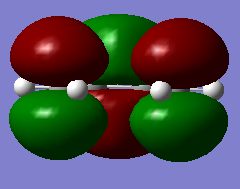
Butadiene			The HOMO is asymmetrical and the LUMO is symmetrical.
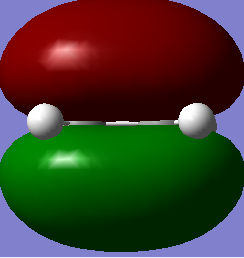
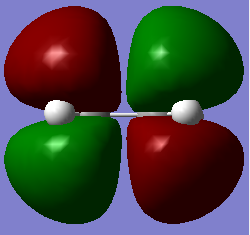
ethylene			The HOMO is symmetrical and the LUMO is asymmetrical.

The Diels-Alder reaction is a cycloaddition that the mechanism involves sigma-overlap π orbitals overlap of the two unsaturated reactants. For the reaction of butadiene and ethylene, 6 π electrons involved which fits the 4n+2 Hückel rule. Theoretically, the reaction can be either all-suprafacil reaction or all-antarafacial reaction for the two components, but it is geometrically impossible for all-antarafacial reaction. For Diels-Alder reaction, the HOMO of one molecule should interact with the LUMO of another molecule in phase. There are two combinations: HOMO of diene + LUMO of ene and HOMO of ene and LUMO of diene. To decide which combination is undergoing, the energy gaps difference can be compared.

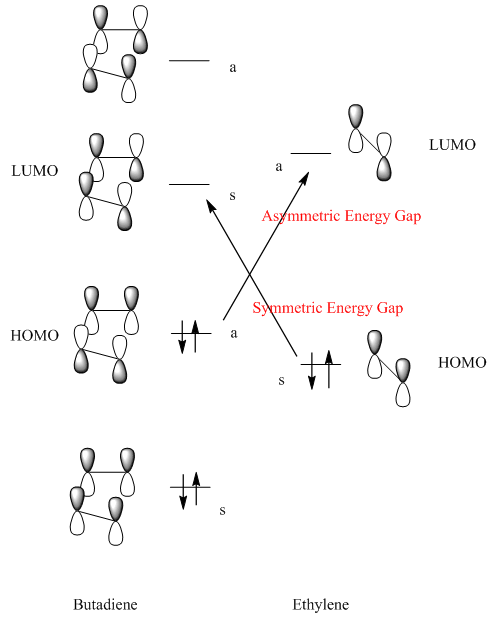The electron transfer can only happen when the symmetry of the two molecular orbitals is the same: asymmetric to asymmetric; symmetric to symmetric.

The energy of HOMO, LUMO of the two reactants were calculated as listed:

Butadiene: HOMO E=-0.34381 LUMO E=0.01707

Ethylene: HOMO E=-0.38777 LUMO E= 0.05284

The energy gap 1 is ΔE=0.05284 - (-0.34381) = 0.3938

The energy gap 2 is ΔE=0.01707 – (-0.38777) = 0.4048

The two energies are close and there should be two combinations of HOMO and LUMO in the reaction. The transition state then has two sets of orbitals which are degenerate as shown in the following table. The energy of s HOMO is -0.32503 and the energy of a HOMO is -0.32389, which are similar. As a result,the HOMO for the transition state is both symmetric and asymmetric. The symmetric one is from the interaction of HOMO of ethylene and LUMO of butadiene; the asymmetric one is from the interaction of HOMO if butadiene and LUMO of ethylene. However, the symmetric transition state HOMO is impossible because there is a nodal plane between the newly forming bond.

As discussed above, asymmetric HOMO of transition state is allowed, so that the interacting orbitals in reactants should be both asymmetric as well. This implied that the HOMO of butadiene is reacting with the LUMO of ethylene.

	asymmetric HOMO	LUMO	symmetric HOMO
Transition State

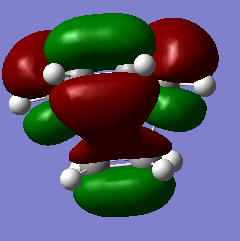
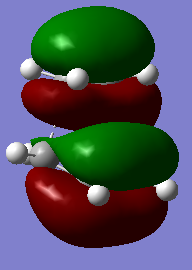
The typical sp³ and sp² C-C bond are 154pm and 147pm respectively.[3] The van der Waals radius of C is 170pm. The two partially formed σ C-C bond in the transition state are 212.02pm and 211.84pm. The partially formed C-C bond is longer than the C-C single bond but shorter than two times of the C van der Waals radius which shows that the bond is forming.

The vibrational frequency that corresponding to the reaction path at the transition state is -818.80nm which is an imaginary frequency. The formation of the two bonds is synchronous which is shown in the animation on the left. The animation on the right modeled the interaction when the frequency is positive (not transition state).

The vibrational frequency ω equals the square root of force constant k over reduced mass m. Frequency is the derivative of surface of potential energy. Energy of transition state geometry is maximum, so that the derivative of energy of transition state is negative. The imaginary frequency, as a result, corresponds to the transition state.

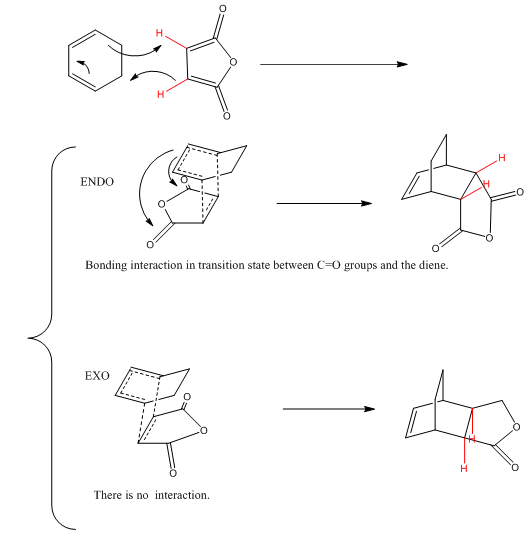
PART 5 Cyclohexa-1,3-diene reacts with maleic anhydride

	TS Structure	Bond Length	Energy	HOMO	LUMO
EXO		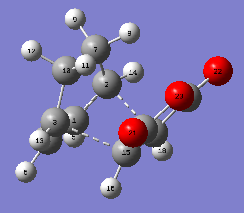C₂-C₁₇=2.17157 C₃-C₁₅=2.16964 C₇-C₂₀=2.94688	E= -0.050419 (AM1 semi-emp)
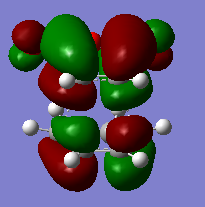
ENDO		C₃-C₁₇=2.16247 C₂-C₁₅=2.16230 C₁-C₁₉=2.89256	E= -0.051505 (AM1 semi-emp)

From the HOMO orbitals of transition state shown above, the electron cloud of carbonyl groups are much closer for ENDO structure than EXO structure. The relative energies of transition state of EXO and ENDO structure were also given in the table above; the transition state energy of EXO is higher than that of ENDO.

The following is the reaction mechanism of the cyclohexa-1,3-diene and maleic anhydride.

The C₇-C₂₀ bond length in EXO structure is 2.94688Å and the C₁-C₁₉ bond length in EXO structure is 2.89256Å. The comparison of the distance suggested that the EXO structure has less steric effect than the ENDO structure. It implies that the EXO transition state is thermodynamic favored.

However, the energy of the transition state of ENDO shown in the table above is lower than that of EXO transition state. The reason of this conflict can be explained by the secondary orbital overlap. Secondary orbital overlap is a molecular orbital consideration for the Endo preference stereochemistry for Diels-Alder reaction. Secondary orbital is the positive overlap of the not active frame in the frontier orbitals. In this example, the Carbonyl groups of maleic anhydride are interacting with the diene. ENDO structure is kinetically favored.

If the reaction is reversible, the major product should be EXO structure. However, this reaction is irreversible and the product is ENDO structure. [4]

Also, the carbonyl bonds in maleic anhydride are electron withdrawing groups which can pull the energy levels of both HOMO and LUMO down. As a result, the LUMO of maleic anhydride will interact with the HOMO of cyclohexa-1,3-diene.

Further discussion:

The solvent, temperature and other conditions are neglected in the calculation of Diel-Alder reaciton. Thermodynamic and kinetic reaction paths depend reaction condition. Also, AM1 method used here is a lower level calculation than HF and B3LP. The number of electrons taken into consideration is less.

Conclusion

In this experiment, transition state modelling was applied to approach the transition state geometry and its energy. As a result, the activation energy, the reaction pathways can be predicted.

For Cope Rearrangement for 1,5-hexadiene, the chair and boat transition states can be modeled by two different methods. The energy of chair transition state is lower than that of boat transition state, which suggested that the rearrangement undergoes the chair transition state geometry.

For Diels-Alder reaction of butadiene and ethylene, the HOMO-LUMO gaps were calculated and the frontier molecular orbitals of reactant and transition state were plotted. Asymmetric-Asymmetric interaction (HOMO of diene reacting with LUMO of ene) and Symmetric-Symmetric interaction (HOMO of ene reacting with LUMO of diene) were both possible by only considering the two energy gaps, which were very close. However, the Symmetric-Symmetric interaction is impossible due to the nodal plane in the newly formed bonds. To sum up, for butadiene and ethylene reaction, only asymmetric interaction of molecular orbitals is allowed.

For Diels-Alder reaction of cyclohexa-1,3-diene and maleic anhydride, the stereochemsitry is analyzed. There are two possible product, one is EXO and the other is ENDO. The EXO one is favored thermodynamically due to the less steric effect; the ENDO is favored kinetically due to secondary orbital overlap and resulted lower transition state energy. This Diels-Alder reaction is irreversible and ENDO is the major product.

Reference

1.Clayden Organic

2.Appendix A

3.van der Waals Volumes and Radii

4.Steric Effects vs. Secondary Orbital Overlap in Diels-Alder Reactions