The Cope Rearrangement Tutorial

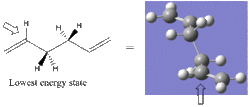
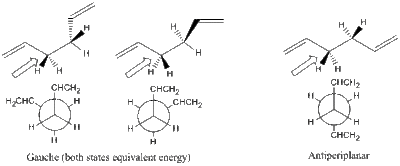
1,5-hexadiene Conformers

This section involves studying all aspects of the COPE rearrangement in GaussView. It is a particularly convenient example due to the reactant and product being identical molecules (1,5-hexadiene). The first step involves determining all possible conformers of this structure, and optimising them in order to determine their relative energies. This is shown as follows:

**Conformers of 1,5-hexadiene including images and energies**
Anti1	-231.69250231	C₂
Conformer Name	Energy /a.u.*	Point Group	Image
Anti2	-231.69253530	C_i
Anti3	-231.68907066	C_2h
Anti4	-231.69097054	C₁
Gauche1	-231.68771613	C₂
Gauche2	-231.69166701	C₂
Gauche3	-231.69266120	C₁
Gauche4	-231.69153033	C₂
Gauche5	-231.68961570	C₁
Gauche6	-231.68916020	C₁

Energy shown is as calculated by the HF/3-21G level of theory

The energy order can be rationalised by looking at optimum angles along the carbon backbone:

Central 4 carbons

Lowest energy in app conformation (C2-C5 dihedral = 180°). This is shown in the following diagram:

Although it is possible to show this using Gaussian (measuring the energy throughout a C3-C4 bond rotation), this was not vital to the exercise. Other energy minima do exist in this rotation (at Gauche conformations; dihedral = 60°), and maxima exist at the eclipsed positions (at 120°, and also where it the molecule is syn-periplanar at 0°). There is more information contained in literature, for example here: Chem. Phys. 106, 5143 (1997)

Terminal 4 carbons

Lowest energy in conformation shown by the example. Occurs where the double bond is orientated as far from the rest of the chain as possible. This can be observed in the rotatable image, obtained by clicking on the following icon.

Higher Level of Theory

A higher level of theory can be used to gain a more accurate picture of the molecular ground state. This takes longer, but is more accurate. Conformer ‘Anti2’, was optimised at the B3LYP/6-31G level of theory giving the following results:

**Anti2 Conformer optimised at a higher method**
Conformer Name	Energy /a.u.	Point Group	Image (showing symmetry)	Spectrum
Anti2	-234.55970424	C_i

Structure Comparison

The optimisation calculation at the higher level of theory gives a representation of the molecular energy on the bare potential energy surface at the minimum.

Using the same level of theory, a frequency job can now be run. This allows for a visualisation of the vibrating molecule to be generated, as well as various energy values, copied straight from the output file, and shown as follows:

Sum of electronic and zero-point Energies= -234.416244 a.u.
Sum of electronic and thermal Energies= -234.408954 a.u.
Sum of electronic and thermal Enthalpies= -234.408010 a.u.
Sum of electronic and thermal Free Energies= -234.447849 a.u.

These energies can be used as a reference for the transition state energies; a table showing the comparison is shown later. The unit for these energies (shown as a.u. on the output file) is hartrees, where 1 hartree = 627.509 kcal/mol.

The calculation can also be completed at 0 Kelvin. This allows for zero-point energy state descriptions of the reaction to be run. These values can then be compared to the values obtained when the program is run at 298 K to determine the effect of temperature on activation energy, and each of the different energies in the output file. As expected, the output file shows difference in all energies with a thermal component, but remains identical in "Sum of electronic and zero-point energies" result.

Optimising the Transition structures

In order to determine the transition state for the rearrangement, an allyl CH-CH2CH structure is first drawn and optimised.

**Optimised Allyl fragment Details**
Structure name:	Allyl Fragment
Image:
Method:	HF/3-21

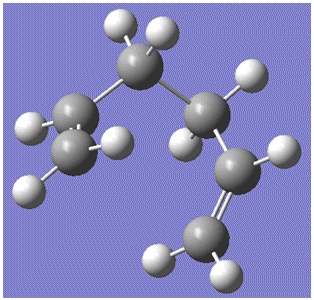
Chair Transition State

Using the optimised allyl fragments shown above, the chair transition state for the process was approximately determined by positioning the two fragments, and then using partial (dotted) bonds in the molecule. The Hessian (force constant matrix) calculation can then be modified; instead of finding energy minima for predicting ground state structures, it can instead find energy maxima to predict transition state geometry. The calculated chair transition state is shown here:

**Optimised Chair Transition State**
Structure name:	Chair Transition State
Image:
Animation (click):
Frequency of TS vibration (imaginary):	-564.31 cm-1
Energy of the transition state /hartrees (298K):	-234.50542741

The 'imaginary frequency' shown for the transition states is a property which confirms that the stucture generated is a transition state. The negative value of the frequency indicates that the vibration away from the average actually reduces the overall energy of the system, indicating that the structure optained is a maximum. There is also significance in there being only one transition state present; if the molecule is slightly different from the transition state, then there is likely to be more than one imaginary vibration. Therefore, this method gives a good way of confirming that the structure obtained is a transition state.

In this case, the initial transition state guess was fairly accurate (probably due to the use of specific atom separations used rather than simple guessing by moving the fragments). If the guess transition state had not caused the transition state calculation to converge, then it may have been necessary to use the ‘Freeze Coordinate’ tool to reduce the extent of the calculation. However, as the transition state was produced from the guess, this was not needed.

Boat Transition State

To determine the boat transition structure, a different method (QST2) was used. Rather than finding the closest maximum to a guess structure, this method determines the transition state by finding the maximum energy state between specified reactants and products.

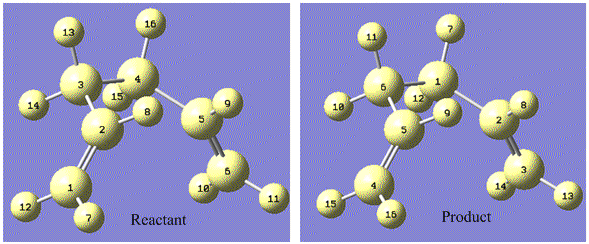
The optimised ‘anti2’ conformer acts as both the reactant and the product in this method. These are opened in the same window by using ‘Add to Mol group’. The two copies of the ‘anti2’ conformer then need to be carefully numbered (by using Edit – Atom List) such that the progression of the Cope rearrangement is represented. However, running the QST2 calculation directly from the structures shown does not give the desired boat transition state product. This is because the two structures are too far from the transition state to converge to it, as processes such as C-C rotation are not considered here. Therefore, the two numbered conformers are redrawn into structures closer to the boat transition state, as shown:

On running the QST2 calculation from here, a structure for the boat transition state is generated. The details of the structure are shown as follows:

**Optimised Boat Transition State**
Structure name:	Boat Transition State
Image:
Animation (click):
Frequency of TS vibration (imaginary):	-508.26 cm-1
Energy of the transition state /hartrees (at 298K):	-234.49289105

Intrinsic reaction coordinate from Chair TS

Finding the minimum energy path from a transition structure down to its local minimum.

The .chk file from the chair transition state was now used in a different way. An IRC job was run in order to work out which conformer of hexa-1,5-diene lies closest to the Cope rearrangement. There are several methods to gaining a complete description of this process. Initially, the calculation was run to 50 points along the IRC in the forward direction, with a single calculation of the force constants. The product of this calculation is shown below:

Alt text — IRC Chair product after 50 points along IRC

It can be easily seen from the diagram that the calculation has not reached the local minimum from the chair transition state, despite taking a long time. Another useful tool is the graphical output from the IRC, which is as follows:

The calculation was therefore repeated with 100 points, but a local minimum was still not reached, giving the product as shown:

This structure clearly shows a progression from the 50 repeats IRC; the partial bonds shown at 50 points are gone, and the individual carbon bonds are formed. Therefore, to finish off the IRC, a simpler optimisation to a minimum calculation at the B3LYP/6-31 level of theory was run, giving the following product:

The image shows conformer 'Gauche2', which indicates that it does reach a minimum. The gauche2 conformer is therefore the closest to the transition state on the IRC.

Other options to gain the appropriate product direct from the IRC could involve running more and more iterations of the IRC until it reaches the product. Alternatively, the same thing could be run with the calculation of force constants at each step; however this takes a very long time.

Calculating the activation energies

Both transition states were then run through an Opt/Freq job (Optimisation and frequency measurements) at the B3LYP/6-31G level of theory. In the results for this calculation, it is possible to gauge the energy of the transition states, and from using the energy minima from the conformers, it is then possible to determine activation energies via each transition state.

Experimental values: Chair = 33.5 ± 0.5 kcal.mol-1. Boat = 44.7 ± 2.9 kcal.mol-1 (at 0K).

Comparison of values computed at 0K to the experimental values. Other analysis

**Energy comparisons between reactant and transition states at B3LYP/6-31 level of theory (in hartrees)**
Structure name:	Electronic Energy	Sum of electronic and zero-point Energies	Sum of electronic and thermal Free Energies (298K)
Anti2 (Reactant/Product):	-234.55970424	-234.416244	-234.447849
Boat TS:	-234.49289105	-234.351363	-234.380802
Chair TS:	-234.50542741	-234.362620	-234.391555
ΔE (Boat):	0.06681319	0.064881	0.067047
ΔE (Chair):	0.05427683	0.053624	0.056294

Using the conversion factor (1 hartree = 627.509 kcal/mol), values for the activation energies are shown. These can be compared with the experimental activation energies, shown in the final column.

**Activation energies summary (in kcal/mol)**
	Electronic Energy difference	0K Activation Energy	298K Activation Energy	Experimental values (from script)
ΔE (Boat):	41.93	40.71	42.07	44.7 ± 2.0
ΔE (Chair):	34.06	33.65	35.32	33.5 ± 0.5

Diels-Alder Cycloaddition

The simplest Diels Alder Process: 1,3-butadiene + ethene

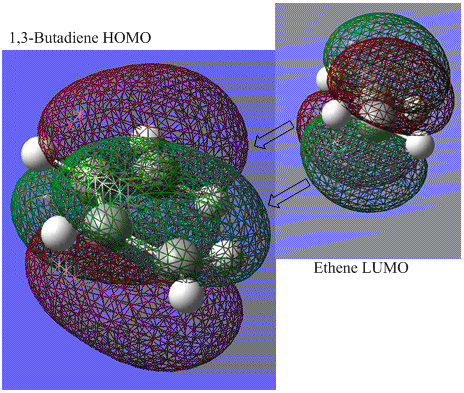
The AM1 semi-empirical molecular orbital method is used for the calculations in this section. Firstly, a molecule of cis butadiene is produced and optimised, before producing visualisations of its molecular orbitals (HOMO and LUMO):

**HOMO and LUMO for the Diels-Alder Cycloaddition**
Orbital:	HOMO	LUMO
Symmetry wrt plane:	antisymmetric	antisymmetric
Image:

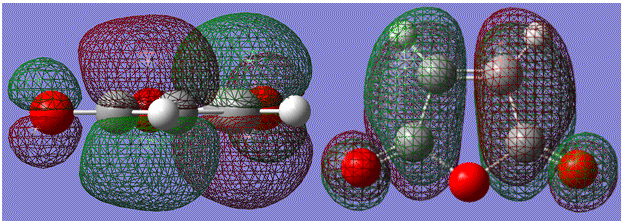
The optimised cis-butadiene structure is then added to an optimised molecule of ethene. The two molecules were then arranged into approximately transition state geometry (by introducing dotted bonds to represent the Diels-Alder transition state). From this guess structure, an optimisation to a TS (Berney) was run with the same method, giving the following result:

Transition state structure:

Transition State for the Diels Alder reaction between 1,3-butadiene and ethene
Molecular Orbitals	HOMO (antisymmetric about nodal plane)	LUMO (symmetric about same plane)
Transition State Structure:	See visualisation.
Imaginary Vibration Frequency:	-956.42
Visualisation (click to show):
Molecular Orbitals

This table shows results from the calculation to determine the transition state in the 1,3-butadiene + ethene Diels Alder reaction. The results confirm expected transition state behaviour for the following reasons:

The structure is symmetrical about a central plane perpendicular to both the ethene C=C and the butadiene C-C
- This plane is the nodal plane in the HOMO, as shown
There is a single imaginary vibration frequency (-956.42)
Animation of this vibration frequency is symmetrical in the same plane (shown by the two .gif visualisations)

Studying the transition state geometry in more detail reveals more about the molecule.

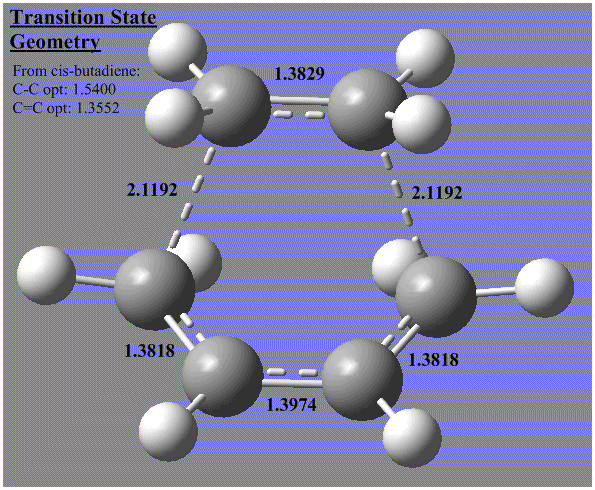
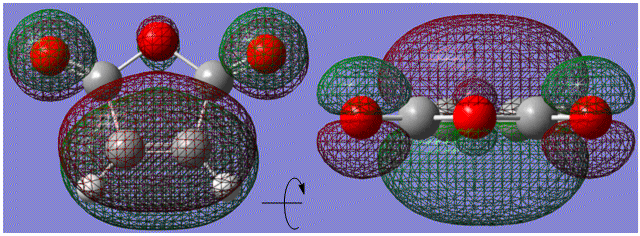
Transition State Geometry:

This image shows all of the C-C distances in the optimised transition state. The diagram also shows reference C-C bond lengths (taken from the optimised 1,3-butadiene structure).

The bond lengths are determined by using the bond editor tool to check the distance between the atoms.

This provides further evidence about the reaction mechanism as follows:

**Observations and Conclusions from transition state geometry**
Observation	Conclusion
New forming bond lengths are equal and greater than C-C single bonds.	Simultaneous and symmetric formation of 2 equivalent single bonds
C=C double bonds from 1,3-butadiene are equal and between the expected lengths of a C-C and C=C bond	Simultaneous and symmetric formation of 2 single bonds from the 2 double bonds
Both other bonds are also between the expected bond lengths for a C-C and C=C	Simultaneous and symmetric formation of 2 single bonds from 2 double bonds
C=C double bonds from butadiene are equal and between the expected length of a C-C and C=C bond. However the old ethene C=C is shorter than the butadiene C-C	Transition state does not lie 'half-way' between reactants and products (assuming ethene C=C ~ cyclohexene C=C) and in fact, an early transition state is observed.

In fact, all the bonds except the newly forming single bonds are much closer to double than single bonds. This is another good indicator for an early transition state.

Instead of using the regular, computed C-C and C=C bond lengths from 1,3-butadiene, we can equally use literature (J. Phys. Chem., 1964, 68 (3), pp 441–451) values for the Van De Waals radius of a carbon atom (1.54 Angstrom). However, this does not greatly change the conclusions from the estimates made based on computed data.

The following diagram shows the frontier orbital interactions responsible for the Diels-Alder process:

It shows how both orbitals have matching asymmetrical properties about the central plane (seen in previous diagrams), and are therefore able to have efficient overlap and form good now bonds.

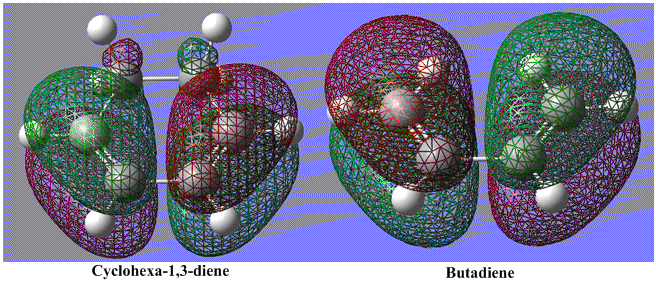
The concepts established here will now be applied to a slightly more complex system involving maleic anhydride as the dieneophile (replacing ethene), and with cyclohexa-1,3-diene as the diene (replacing 1,3-butadiene).

The Diels Alder Reaction of maleic anhydride with cyclohexa-1,3-diene

In this section, a slightly more complex Diels-Alder process is studied. In general, the process mirrors the 1,3-butadiene + ethene system very well. However, it is in the difference between the systems where the most interesting observations can be made.

Comparison

The HOMO orbitals of the two diene species are very similar. The addition of the extra -CH₂-CH₂- group is mainly to fix the conformer of the product with a ring, allowing the exo and endo states to form.

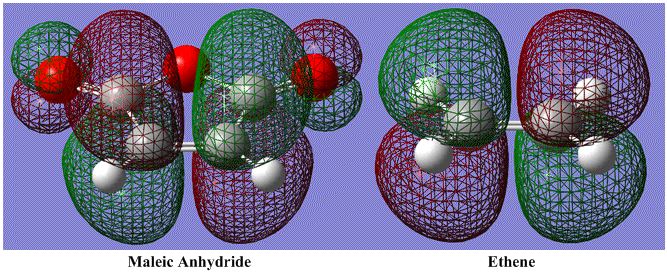
There is more difference between the orbitals of the dieneophiles. The electronegative oxygen atoms distort the fronteir orbitals involved in the Diels-Alder process. This is shown in the following diagram:

As with before, the same two orbitals are involves in the reaction. The similarity is best seen here, with the diene HOMO and the dieneophile LUMO shown next to each other. The dieneophiles (LUMOs, top diagram) map down vertically onto the dienes (HOMOs, bottom diagram). The efficient orbital overlap can be seen in both cases, and the process occurs as before.

When viewing the comparison horizontally instead of vertically, it is clear that the differences in the diene itself are small. In fact the only difference is that there is a very small amount of the orbital which occurs on the non-involved Carbon atoms. The major difference comes in viewing the diene LUMOs. It is clear that the presence of the oxygen atoms in the maleic anhydride is changing the diene LUMO. This change will now be studied further.

The transition state of the Diels-Alder reaction here can be shown as before. However, this time there are 2 possible products: the exo- and the endo- product. The transition states en route to each of these products is shown below:

Visual Results

**Comparison of exo and endo transition states and products**
Product:	Endo	Exo
Total energy:	-0.16017085	-0.15990941
Image of product:
Transition state: (click to animate vibration)
Single imaginary vibration frequency:	-806.33	-812.17
Transition state HOMO:
Transition state energy: (a. u.)	-0.05150480	-0.05041985

As previous, the vibration confirms that the process occurring is happening concertedly, with both new C-C bonds forming simultaneously as with the previous example.

Numerical Results

The energies of the processes are summarised as follows:

**Energy comparison for Diels Alder reactions to exo and endo products (in hartrees)**
Structure name:	Electronic Energy	Sum of electronic and zero-point Energies	Sum of electronic and thermal Free Energies (298K)
Exo product :	-0.15990941	-234.416244	-0.002886
Endo product:	-0.16017085	-234.351363	-0.003162
Exo TS:	-0.16017085	-234.362620	0.099118
Endo TS:	-0.0515048	-234.362620	-0.102004
ΔE (Exo):	0.00026144	-0.10318	0.067047
ΔE (Endo):	-0.108666	-0.102031	-0.100513

**Activation energies summary (in kcal/mol)**
	Electronic Energy difference	0K Activation Energy	298K Activation Energy
ΔE (Endo):	-68.19	-64.03	-63.07
ΔE (Exo):	-68.93	-64.75	-64.01

The table shows that the endo product has both the lower energy transition state, and the lower energy product. Therefore the activation is also smaller (by 0.96 kcal/mol) which explains why this is the thermodynamically more stable and favoured product. This generally in agreement with literature, except that literature data shows the exo product being lower in energy than the endo product when computed: Chem. Ed., 81, pp. 1633-36 (Nov. 2004)

Discussion

The major cited reason why the endo-isomer is more stable is due to the secondary orbital overlap. This occurs due to an interaction between molecular orbitals adjacent to the newly forming bonds (from the maleic anhydride -(C=O)-O-(C=O)- fragment to the diene carbons which eventually become the double bond). This is the very common explanation used in teaching and literature.

However, it is clear from the maleic anhydride HOMO that a nodal plane exists within this region, so any expected orbital interactions here would be expected to be at a minimum. However, it is possible that interactions between other lower lying molecular orbitals causes this effect.

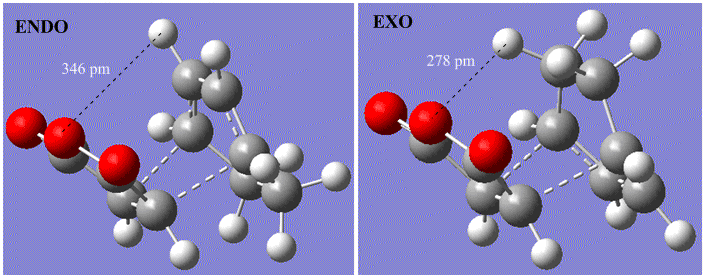
However, it is possible to offer a simple explanation based on the atom spacings in the product molecules. In the endo form, the maleic oxygen groups have a nearest through-space neighbour of the hydrogen atoms attached the sp₂ carbon atoms. In contrast, the exo form has the maleic anhydride structure lying closest to hydrogen atoms attached to sp₃. The distance between the central maleic oxygen and these H atoms is 2.78 Angstrom in the exo transition state and 3.46 Angstrom in the endo transition state. This would suggest, even without any secondary orbital overlap, that the endo product is favoured of the exo product.