Cope Rearangement Tutorial

Anti1

The molecule was drawn in GaussView with the center bonds anti.

The structure was then cleaned up and the molecule optimised using a HF/3-21G method. The results are detailed in the table below.

Conformer	Structure	Point Group	Energy/Hartree HF/3-21G
anti 1		C₂	-231.69260

This isomer matches the "anti1" listed in appendix 1 both in terms of energy and point group.

Gauche1

The following gauche conformer was drawn as before, the structure cleaned up and the molecule optimised using a HF/3-21G method. The results of this calculation are shown below.

Conformer	Structure	Point Group	Energy/Hartree HF/3-21G
gauche 1		C₂	-231.69153

This isomer matches the "gauche4" listed in appendix 1 both in terms of energy and point group. As expected it is higher in energy than the anti-periplanar structure that was optimised before it, due to increased steric clash between the bulky alkene substituents.

Conformer of Lowest Energy

From previous knowledge the conformer of lowest energy should be antiperiplanar

Anti 2

The Anti2 conformer was drawn in GaussView by carefully selecting which gauche hydrogen to attach the the next fragment to.

The structure was cleaned and then optimised at the HF/3-21G level.

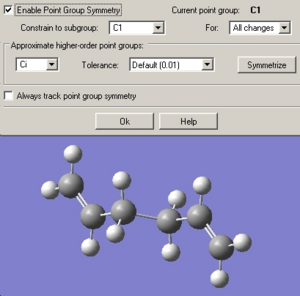
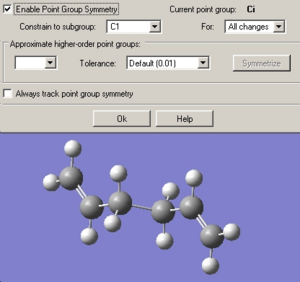
Despite resulting in a molecule that resembled the “ani2” structure (see picture below) in both form and energy, the symmetry given by the “Results Summary” from the .out file suggests a point group of C₁ not C_i.

The .chk file was therefore opened and the molecule was symmetrised by clicking the edit->Symmetrise function. This resulted in a C_i point group.

Since the molecule appeared to be as described in the table, it was further optimised at the B3LYP/6-31G* level. By selecting the DFT method, B3LYP then 6-31g +(d) basis set. This required considerably more computing power and the resulting molecule is shown below compared with that using the HF/3-21G.

!Theory Level|Molecule|Symmetry|Enegry(A.U.)|

Theory Level	Structure	Symmetry	Energy/Hartree
HF/3-21G		C_i	-231.69254
B3LYP/6-31G*		C_i	-234.62319

Not surprisingly this improved level of theory vastly decreased the minimum energy of the molecule whilst keeping its symmetry the same.

Lastly in order to compare the results with some experimental values a Frequency calculation needs to be run. This was done at the same level of theory by simply changing the method to frequency under the Calculation tab.

The results were checked to see if all frequencies were positive. The picture below shows that this is indeed the case.

The required energies were visualised in the log file and are shown below.

Sum of electronic and zero-point Energies=           -234.481066
Sum of electronic and thermal Energies=              -234.473717
Sum of electronic and thermal Enthalpies=            -234.472773
Sum of electronic and thermal Free Energies=         -234.512621

The calculation was repeated at 0K by adding the addition keywords "Freq=ReadIsotopes" and inserting the following text at the ned of the .gjf input file.

0.0 1.0
12.0
1.0
1.0
12.0
1.0
1.0
12.0
1.0
12.0
1.0
1.0
12.0
1.0
12.0
1.0
1.0

The first line refers to the temperature (0.0K) and pressure (1 bar).

The resulting .log file was examined and the results are displayed below.

Optimizing the "Chair" and "Boat" Transition Structures

Method1

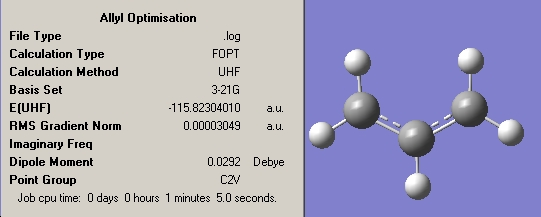
The following allyl fragment was drawn in GaussView and optimised at the HF/3-21G level.

The results of the optimsation are also shown below.

The optimised fragment was copied twice into anew window by using the Edit->Paste->Apend Molecule tool. One of the fragments was rotated and positioned as to create the two pointy bits of a chair type conformer. The distance between the bases of these "points was set to 2.2Å. This can be seen below.

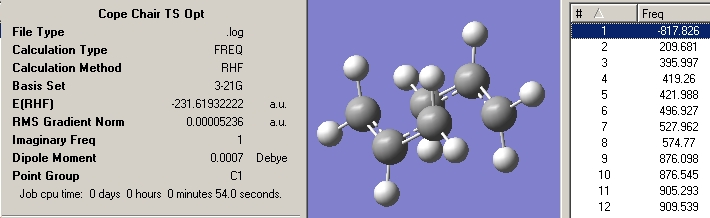
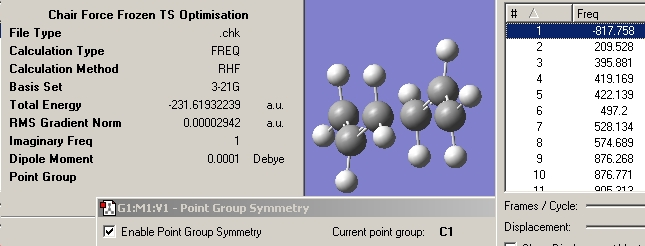
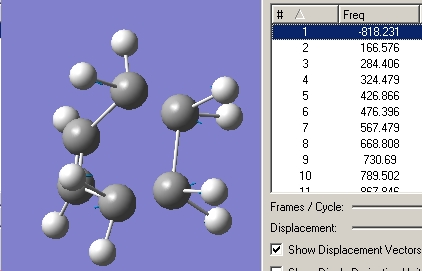
Now using a HF/3-21G method the transition sate was optimised and the frequencies calculated. The force constants option was set to once and the Optimisation was set to a TS(Berny). The additional keywords "Opt=NoEigen" were also added to the method to stop it crashing if two or more negative frequencies are detected. the results are shown in the graphic below.

As expected there is one negative vibration at -818cm^-1. By animating the vibration it can bee seen to follow the same mechanism as the Cope rearrangement. Describing only one half of the vibration, only the carbons move, the two closest to the bottom move closer to each other as if forming a new sigma bond and the two at the top move away hence the gap in the ring. The allyl bonds that these later carbons have also become shorter indicting the presence of a π bond forming.

Force Frozen Method

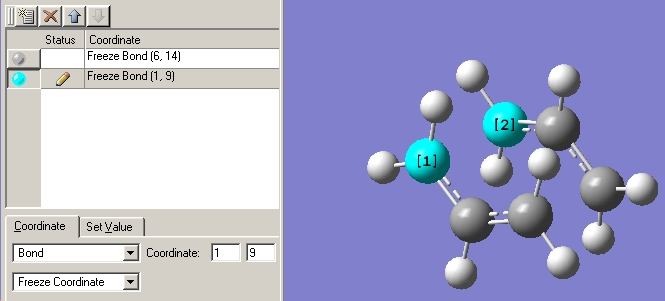
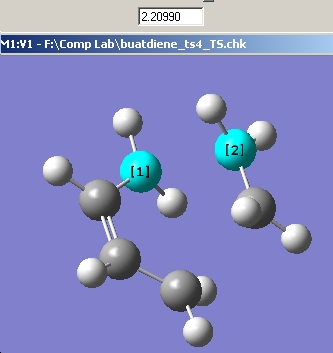
A transition state fragment was created in the same way as before. Using the Redundant co-ordinate editior the terminal carbons of the fragments were set to a distance of 2.2Å and frozen. This is shown below.

The molecule was then optimised at the HF/3-12G level it was noticed that this time the "Opt=ModRedundant " had already been inserted into the imput line. The output .chk file was opened and it was found that the desired bonds had been set to a length of 2.2Å. (No grphic of this is shown as it is a simple procedure).

The same bonds that were previously frozen were in the same way altered, using the Redundant Co-ordinate editor, to Bonds and Derivatives, thus allowing thier distance to change. The transition sate was then optimisaed (N.B. keywords Opt=NoEigen) but the force field was not calculated.

The resulting molecule is shown below. The bond lengths between the terminal ends of the alkyl fragments are 2.02074 and 2.0269Å

QST2 Method

The optimised "anti2" hexadiene molecule was copied from the previous part of the experiment into a new Gaussian window. An addition separate molecule was then added by selecting the File->New-->Add to MolGroup option and pasting another of the optimised anti2 molecules. This second molecule is going to be the product and so needs to be numbered as if the reactant has undergone the Cope rearrangement. This is quite tricky as the molecule needs to eb ine correct orientation (and it is non planar!) and the atoms must be changed in the correct order. To help me do this it was first worked out in rough and with significant help form the lab script the result is shown below.

This arrangement was subjected to a Optimisation anfd Frequency calculation but this time to find a TS (QST2) transition state. (N.B. the additional keywords "Opt=NoEigen" or the link dies) Now as intimated in teh lab script this calculation is expected to fail. Examining the output file it is easy to see that the calulation has completely failed.

The structure is rather interesting though, analogous to a sort of planar twist-boat.

Diels Alder

Introduction

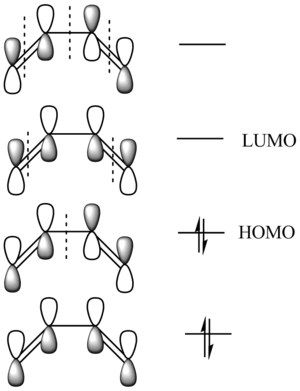
Beofre any clculations are carried out let us construct a MO diagram for butadiene formed purely from p orbitals.

this is what we expect the aklculated orbitals to look lke. It is easy to see that the HOMO should be antisymmetric in the a line bisecting teh molecule (co-incdent witht the node shown by a dotted line) and that the LUMO should be symmetric.

Experimental

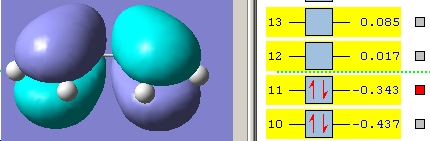
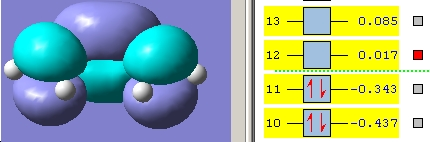
The butadiene was drawn in GaussView (see above), cleaned using the Edit->Clean function and the molecule optimised at the AM1 level. This low level of theory is used since the energies are not important in this part of the investigation, purely the shapes of the HOMO and LUMO. The HOMO and LUMO were visualised by opening the .chk file and accessing the Edit->MO's menu. The results are shown below.

The symmetries of these orbitals are co-incident with those predicted with from the qualitative MO diagram in the introduction.

Handbook of Chemistry & Physics 65th Edition CRC Press ISBN 0-8493-0465-2

In an effort to locate the transition state several approaches were embarked upon. the first involved creating an ethene type fragment and locating it over the butadiene type fragment and optimising the TS simply by running a calculation. This failed so the frozen co-ordinate method was tried instead.

The following molecule was drawn and the terminal bonds of each fragment frozen by using the Redundant Coordinate Editor and changing the options to Bond and Frozen. The distance was set to 2.2Å since this is longer than the standard C-C bond distance of 1.50Å. This molecule was optimisaed at the HF/3-21G level. The result was examined and looked promising so a transition state optimisation (Opt+Freq to TS Berny) was then carried out. Force constants were not calculated and the additional keyword O"pt=NoEigen" was included. The co-ordinates that had previously been frozen were changed to Bonds and derivative and their length was not restricted.

This produced the following transition stae with one negative vibration. The distance between the terminal carbonsin each fragment is shown at the top of the second graphic.

The inter fragment distance is larger than the sp³ sp³ C-C bond distance of 1.54Å and even larger than the sp²-sp² length of 150Å. This suggests that the new bond will be sp³-sp³ hybridised since a much shorter distance is expected in case of a double bond. The displacement vectors are shown for the negative vibration and form these and the graphic it can be seen that the mode is synchronous. The first positive frequency exhibits an asynchronous rocking motion however.

The HOMO (first graphic)and LUMO for this fragment were also visulaised to determine their symmetry.

It is easy to see that the HOMO is anti symmetric about the central plane of the molecules and the LUMO is symmetric. The π* orbital of the ethylene fragment and the HOMO of the butadiene fragment (both antisymmetric) have combined to form an antisymmetric HOMO for the transition state. This confirms the hypothesis that only orbitals of the same symmetry can overlap to form an orbital of the same symmetry. It is also consistent with the qualitative diagrams that were drawn in the introduction.

References Anti 1 https://www.ch.ic.ac.uk/wiki/images/5/5a/Jfg_HEXADIENE_ANTI1.LOG
Gauche 1 https://www.ch.ic.ac.uk/wiki/images/e/e4/Jfg_HEXADIENE_GAUCHE1.LOG

Experimental Diels Alder with Maleic Anhydride

Before any calculations in GaussView were completed the Maleic Anhydride fragment was drawn in ChemDarw3D, optimised and saved as an Gaussian Imput file. The lines starting with LP were seleted, the file opened in GaussView and the molecule optimised again by jusing the clean function. In a seperate window a bicyclic system was drawn and optimised using the Clean function. Part of the ring was deleted and the maleic anhydride fragment added by using the Edit->Paste->Append molecule function. The C=C double bond in the maleic anhydride was changed for a single bond as is would be in the transition state and the fragment orientated into a endo or exo form. This resulted in the follwoing molecules where the terminal ends of each fragment were editied using the Redundant Co-ordinates editior.

As shown above they were set to "Bonds" and "Freeze Co-ordinates" witht their length set to 2.2Å.

The molecule was optimised at the