Rep:Mod:jf301
Report
Optimisation of NH3
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy, E(RB3LYP): -56.55776873 a.u
RMS gradient: 0.00000485 a.u
Point group: C3V
NH bond length of final optimised structure: 1.01798 Å
HNH bond angle: 105.741 degrees
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986278D-10
Optimization completed.
-- Stationary point found.
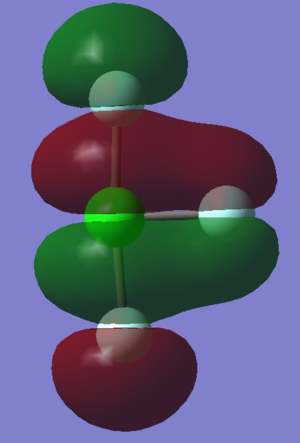
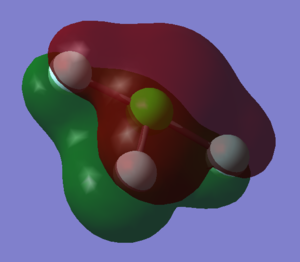
Interactive NH3 model
Optimised NH molecule |
File:JFGRIFFIN NH3 OPTF POP.LOG
Vibrational analysis
From the 3N-6 rule, (3*4)-6=6 vibrational modes are to be expected. There are two pairs of degenerate modes: modes 2 and 3 are degenerate, and modes 5 and 6 are degenerate. This can be determined from the frequency values in the table. Vibration modes 1, 2 and 3 are bending vibrations. Vibrations modes 4, 5 and 6 are stretching vibrations. Vibrational mode 4 is a highly symmetric stretch of all three NH bonds, simultaneously and in phase. Vibrational mode 1 is the "umbrella" mode; all three NH bonds are bending in the same direction. Two bands are to be expected in the IR spectrum of ammonia, due to the change in dipole moments in vibrational modes 1, 2 and 3 - modes 2 and 3 are degenerate and so contribute to the same signal in the spectrum.
The charge associated with the Hydrogen atoms in the molecule is 0.375 and for the singular Nitrogen atom it is -1.125. Due to the symmetry of the molecule it is to be expected that all three Hydrogen atoms have the same charge, and that the sum of these positive charges must indeed be equal and opposite to the charge on Nitrogen, given that ammonia is a neutral molecule. It is also sensible that the program has predicted a negative charge for nitrogen, seeing as this is a more electronegative atom than hydrogen.
Optimisation of N2
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy, E(RB3LYP): -109.52412868 a.u
RMS gradient: 0.00000060 a.u
Point group: D*H
NN bond length of final optimised structure: 1.10550 Å
NN bond angle: Linear moecule, 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400910D-13
Optimization completed.
-- Stationary point found.
Interactive N2 model
Optimised N molecule |
Vibrational Analysis
A vibration frequency of 2457.33 cm-1 is found for the molecule. This corresponds to the symmetric stretching of the bond. This vibration results in no change in dipole and as such will not be IR active.
Optimisation of H2
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy, E(RB3LYP): -1.17853936 a.u
RMS gradient: 0.00000017 a.u
Point group: D*H
NH bond length of final optimised structure: 0.74279 Å
HH bond angle: Linear molecule, 180 degrees
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
Interactive H2 model
Optimised H molecule |
Vibrational Analysis
A vibration frequency of 4465.68 cm-1 is found for the molecule. This corresponds to the symmetric stretching of the bond. This vibration results in no change in dipole and as such will not be IR active.
The Haber-Bosch Process
Energy Values in a.u
E(NH3)= -56.55776873 2*E(NH3)= -113.11553746 E(N2)= -109.52412868 E(H2)= -1.17853936 3*E(H2)= -3.53561808 ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579070 (8dp)
Energy Values in kJ/mol
E(NH3)= -148492.43 2*E(NH3)= -296984.87 E(N2)= -287555.62 E(H2)= -3094.26 3*E(H2)= -9282.77 ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.48 (2dp)
Energy calculation and analysis
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.48 (2dp)
This is the energy calculation for the formation of 2 moles of ammonia, therefore for the formation of 1 mole:
ΔE= -146.47848285/2 = -73.24 kJ/mol
Energy is lost as heat when moving from reactants to products; the Haber-Bosch process is an exothermic process. This indicates that the ammonia product is more stable than the gaseous reactants.
The literature value for the H2 bond strength is 435.7799 kJ/mol[1]. This differs from the computer approximated value of 3094.26 kJ/mol. This indicates that there is error in the approximation. A possible reason for this may be that in setting certain parameters for the approximation to be run at, the accuracy of the calculations may be limited. Additionally, literature values are usually reported at standard conditions but it is unknown how the computer program accounts for the effects of the atmosphere.
Optimisation of ClF3
Calculation method: RB3LYP
Basis Set: 6-31G(d,p)
Final energy, E(RB3LYP): -759.46531688 a.u
RMS gradient: 0.00002645 a.u
Point group: C2V
ClF bond lengths in final optimised structure: Two of length 1.72863 Å; these are the fluorine atoms bonded in the vertical axis. One of length 1.65146 Å, in the equatorial plane.
FClF bond angle: 87.140 degrees
FClF bond angle, using fluorine atoms in the vertical axis: 174.281 degrees
Item Value Threshold Converged?
Maximum Force 0.000050 0.000450 YES
RMS Force 0.000028 0.000300 YES
Maximum Displacement 0.000204 0.001800 YES
RMS Displacement 0.000134 0.001200 YES
Predicted change in Energy=-1.250248D-08
Optimization completed.
-- Stationary point found.
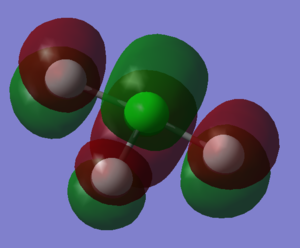
Interactive ClF3 model
Optimised ClF molecule |
The molecule adopts a trigonal bipyramidal structure centered around the chlorine atom. Two fluorine atoms are bonded to opposite sides of the chlorine atom; this is the vertical axis. Another fluorine atom is bonded in the equatorial plane. Two lone pairs are also placed in orbitals in the equatorial plane. The molecule therefore adopts a 'T' shape.
The central chlorine atom has a calculated charge of 1.225. The two fluorine atoms bonded in the vertical axis are symmetrically identical and therefore have the same charge associated with them: -0.454. The fluorine atom bonded in the equatorial plane has a charge of -0.316. It is sensible for the vertical axis fluorine atoms to have a greater negative charge associated with them; this means electron density is more concentrated at 90 degrees away from the plane, and therefore from the electron lone pairs, rather than the ~120 degrees that the equatorial fluorine atom can provide.
Vibrational Analysis
By the 3N-6 rule for non-linear molecules, 3*(4)-6=6 vibrational modes are to be expected. Modes 1, 2 and 3 are bending modes and 4, 5 and 6 are stretching modes. The frequency values indicate that non of the modes are degenerate.
Molecular Orbitals
| Molecular Orbital Diagram | Description |
|---|---|
 |
This is the lowest energy molecular orbital of ClF3. Molecular orbitals are the combination of atomic orbitals. The valence electrons are those that are involved in bonding. Chlorine has valence electrons in orbitals with n=3 and fluorine has valence electrons in orbitals with n=2. There are no nodes at any of the atom centres; this tells us that this molecular orbital is a combination of 's' orbitals, as these do not have nodes. The calculated model of this molecular orbital assigns electron density along the three inter-nuclear axes, which indicates that this is a bonding orbital with respect to all three of the bonds in the molecule. |
 |
This molecular orbital appears to be the combination of a 'p'-orbital of the central chlorine atom, with the '2s' orbitals of the fluorine atoms bonded in the vertical axis. |
 |
This molecular orbital appears to be the combination of a 'p'-orbital of the central chlorine atom, with '2p'-orbitals of all of the fluorine atoms. This can be deduced when the nodes of the molecular orbital are considered. 'P'-orbitals have nodal planes which cut through the centre of the atom; this helps to identify when a 'p'-orbital is contributing to a molecular orbital. All four of the 'p'-orbitals which are contributing to this molecular orbital are in the same orientation in space - they are all pointing along the same axis. |
 |
This is another combination of p-orbitals, but they are aligned in a different axis to the previous molecular orbital. |
 |
This is the HOMO of the molecule. Again it can be seen that this is a combination of 'p'-orbitals. However, the system has modeled this orbital to have nodal planes of electron density between all of the atoms respectively. This is therefore anti-bonding with respect to all of the bonds within the molecule. |