Rep:Mod:jem3i
Jenifer Mizen: Transition States and Reactivity (Module 3)
Cope Rearrangement
The transition structure of the Cope rearragement was investigated here.
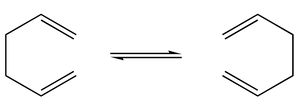

Firstly, 1,5-hexadiene with an approximately anitiperiplanar (a.p.p.) relationship between the four middle carbon atoms was optimised using HF/3-21G (a Hartree-Fock method with the 3-21G basis set). The energy found by the summary was -231.68540au and the molecule was found to have C2h symmetry. The energy gradient and output files were both checked to ensure that convergence had been achieved.
Item Value Threshold Converged? Maximum Force 0.000058 0.000450 YES RMS Force 0.000023 0.000300 YES Maximum Displacement 0.001543 0.001800 YES RMS Displacement 0.000697 0.001200 YES Predicted change in Energy=-2.752863D-07 Optimization completed. -- Stationary point found.
This was repeated for a molecule in which the central carbons were gauche to each other. The energy was expected to be higher, as the a.p.p. conformation is generally the lowest in energy due to favourable interaction between the C-C (or C-H)σ-orbital and the neighbouring C-C (or C-H) σ*-orbital. The orbital overlap is best for the a.p.p. conformation compared to e.g. gauche.[2]However the optimised energy was found -231.69153 au and the symmetry was C2.
The two conformations are shown below:
A.p.p |
gauche |
.

The gauche structure corresponds to Gauche4 in Appendix 1. The initial antiperiplanar structure had the same symmetry as Anti3, but a different structure and slightly different energy. It was most similar to Anti1. A slightly different starting geometry was used and optimised to the anti1 conformation:
Antiperiplanar 1 |
This then gave the same point group and energy as anti1.
The Gauche structure was lower in energy than the antiperiplanar. This can be rationalised by considering the pi orbital interacting with the vicinal proton. Newman projections make it easier to visualise this interaction. Here, "D" corresponds to the minimum energy conformation (i.e. gauche 3 in the appendix 1).
.[4]
In the gauche form it was found that the distance between the terminal hydrogen (on the double bond) and a hydrogen on the third carbon atom was 2.44A, which corresponds to a van der Waals attractive interaction, (an A1,3 eclipsed conformation). Overall, the σ-C-H/π*C=C interaction was responsible for the lower energy of the gauche form The lowest energy conformation (D) was then optimised and is shown below:
Gauche 3 |
This has the same energy and point group as gauche 3 in appendix 1.
Next, the Ci anti2 conformation was optimised, and the symmetry checked to ensure it had stayed the same. The energy was found to be -231.69254au. This is the same as that given in the table. The molecule was then re-optimised, this time using the more accurate B3LYP/6-31G* level. The energy became more negative at -234.55970au.
| 1234 dihedral angle /o | 2345 dihedral angle /o | 1-2 & 5-6 bond length /A | 2-3 and 4-5 bond length /A | 3-4 bond length/A | |
|---|---|---|---|---|---|
| 1st optimisation | 114.7 | 180.0 | 1.32 | 1.51 | 1.55 |
| 2nd optimisation | 118.7 | 180.0 | 1.34 | 1.51 | 1.56 |
1st optimisation |
2nd optimisation |

For both, the 1234 dihedral angle was the same magnitude, but a different sign to the 3456 dihedral angle. This angle increased somewhat on the second optimisation, but there were no other particularly significant changes to the geometry.
Next, a frequency analysis was done using the same B3LYP/6-31G* level. This meant that additional thermochemistry data could be found, as well as the IR frequencies. No negative frequencies were found, with the lowest being at 71.69cm-1.
Thermochemistry data:
Sum of electronic and zero-point energies (potential energy at 0K) = -234.416244 au.
Sum of electronic and thermal energies (energy at 298.15K and 1atm, with contributions from translational, vibrational and rotational energy modes) = -234.408953 au.
Sum of electronic and thermal enthalpies (with correction for RT, H=E+RT) = -234.408009au.
Sum of electronic and thermal Free Energies (including entropy G=H-TS) = -234.447852.
Optimising the Chair and Boat Transition Structures
Chair
Firstly, the allyl fragment was optimised (HF/3-21G). Then two of the optimised fragments were put together to give the approximate structure of the transition state. This was then optimised using two different methods:
1. Computing the force constant matrix (or the Hessian). This works well if the guess of the TS is very similar to the true structure.
HF/3-21G was used as before, and an Opt+Freq calculation done , with optimisation set to TS(Berny). To ensure that it did not crash if more than one imaginary frequency were found, "Opt=NoEigen" was added in the additional keywords section. An imaginary frequency was found at 818cm-1. The vibration and the TS are shown below:
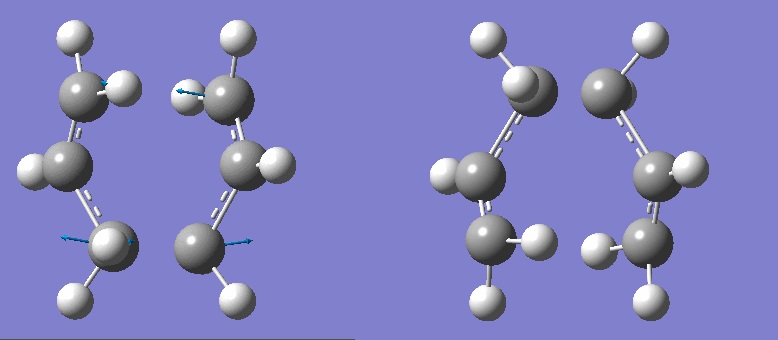
TSforChairOptforwiki.mol |
On Gaussview, a dotted line was shown between the carbons, instead of one double and one single bond. This did not appear using the jmol view, however the "single" and "double" bonds shown are actually the same length.
2. Freezing the reaction coordinate (so the rest of the molecule can be optimised), then unfreezing and re-optimising. This time, the distance between the terminal carbons of each fragment was set to 2.2A. The molecule was then re-optimised to give a result identical to when using the previous method. The distance between the terminal allyl carbons i.e. where the new bond will form, was found to be 2.02A.
Boat
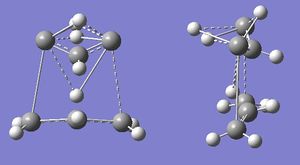
Next, the boat TS was optimised. Initially the QST2 method was used. Two of the Ci anti2 molecules previously optimised were used and the atoms numbered so that the reactant and the product labelling matched. An Opt+Freq calculation was done, and the job failed, giving the following output:
Failed optimisation for boat TS.mol |
QST2 did not take into account the possibility of rotation about the central bonds, so failed to find the TS structure. The input was therefore modified so that the reactant (left hand side) and product (right hand side) had the configurations shown. The QST2 job was re-run. This gave error number 2070, and, when the .chk file was opened, Gaussview stopped responding. When the .out file was opened, it gave a "Gaussian error detected line number 1314" message, and the structure shown.
This has evidently not worked either. QST2 is very sensitive to how close the inputted structures are to the TS, so there may have been an error in the input file.
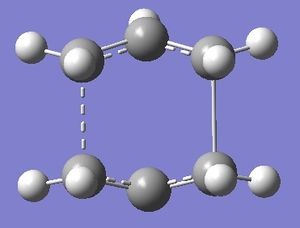
The calculation was redone using QST3, and providing a guess for the TS. In this case, the exact geometries of the structures inputted were not quite as important as for QST2. This gave the TS structure shown, and C2v symmetry.
The Gauche1 conformation in Appendix 1 appears to be the most suitable for the Cope rearrangement, as the two terminal carbons are closest together, and it resembles the TS the closest.
IRC
Next, the intrinsic reaction coordinate method (IRC) was used.
Chair TS initial IRC |
The first time this was used, a minimum geometry was not reached and the calculation was redone using three different methods:
1. The final structure given after the initial IRC was run was optimised.
2. The IRC calculation was repeated with 100 points (doubling the number compared to the initial calculation).
3. The calculation was repeated and force constants were calculated at each step.
Method 1. |
Method 2. |
Method 3. |
Method 3. should be the most reliable, however it took the longest amount of time to run.
| C-C forming bond length/A | |
|---|---|
| Initial IRC | 1.57, 2.90 |
| IRC method 1. | 2.17, 4.39 |
| IRC method 2. | 1.56, 3.28 |
| IRC method 3. | 2.02, 2.02 |
The bond forming length found using method 3. is the same as when the TS was optimised previously. This, and the result from the QST3 method both suggest concerted reactions, whereas the other methods do not.
Activation energies for the reaction via both boat and chair TS
The TS structures were reoptimised using the B3LYP/6-31G(d) level, starting from the HF/3-21G Hessian method optimised structures already found. Geometries: Chair: C-C bond forming distance: 2.20A, C-C bonds 1.40A, C-C-C angle: 122.4o. This compares to the 2.02A, 1.39A and 120.5o found at the lower level of theory. The main difference was the increased C-C bond forming length. Boat: C-C bond forming distance 2.23A for both pairs of carbons. All other C-C bonds 1.38A. C-C-C bond angle 122.6o. The previous data found at the lower level of optimisation was: C-C bond forming distance 2.14A, C-C bond lengths 1.38A, C-C-C angle 121.6o. Again, the main difference was the increased C-C bond forming distance.
Chair: Initial lower level optimisation:
Zero-point correction= 0.152623 (Hartree/Particle) Thermal correction to Energy= 0.157983 Thermal correction to Enthalpy= 0.158927 Thermal correction to Gibbs Free Energy= 0.124771 Sum of electronic and zero-point Energies= -231.466700 Sum of electronic and thermal Energies= -231.461340 Sum of electronic and thermal Enthalpies= -231.460396 Sum of electronic and thermal Free Energies= -231.494551
Higher level optimisation:
Total energy from summary file -234.55868305au Zero-point correction= 0.143369 (Hartree/Particle) Thermal correction to Energy= 0.150625 Thermal correction to Enthalpy= 0.151569 Thermal correction to Gibbs Free Energy= 0.111606 Sum of electronic and zero-point Energies= -234.415314 Sum of electronic and thermal Energies= -234.408058 Sum of electronic and thermal Enthalpies= -234.407114 Sum of electronic and thermal Free Energies= -234.447077
There were no imaginary vibrations in the IR.
Boat: Lower level optimisation:
Zero-point correction= 0.151870 (Hartree/Particle) Thermal correction to Energy= 0.157500 Thermal correction to Enthalpy= 0.158444 Thermal correction to Gibbs Free Energy= 0.123025 Sum of electronic and zero-point Energies= -231.450932 Sum of electronic and thermal Energies= -231.445303 Sum of electronic and thermal Enthalpies= -231.444359 Sum of electronic and thermal Free Energies= -231.479777
Higher level optimisation:
Total energy from summary file -232.79730444au Zero-point correction= 0.141550 (Hartree/Particle) Thermal correction to Energy= 0.147856 Thermal correction to Enthalpy= 0.148800 Thermal correction to Gibbs Free Energy= 0.112783 Sum of electronic and zero-point Energies= -234.351364 Sum of electronic and thermal Energies= -234.345059 Sum of electronic and thermal Enthalpies= -234.344114 Sum of electronic and thermal Free Energies= -234.380132
There was one imaginary vibration in the IR at -504.28cm-1.
These energies are significantly different to each other at the two different levels (1 Hartree = 627.509 kcal/mol).
Activation energies(kcal/mol):
| low level method, 0K | low level method, 298.15K | high level method, 0K | high level method, 298.15K | |
|---|---|---|---|---|
| chair | 45.71 | 44.69 | 33.82 | 33.76 |
| boat | 55.60 | 54.76 | 73.95 | 73.29 |
Experimental values at 0K were 33.5 +- 0.5 for the chair and 44.7+-2.0 for the boat. The values found for the boat at the higher level of optimisation were very different, suggesting that this calculation may not have worked. However for the chair, the higher level shows the value the same as the experimental one for the higher level of calculation (whereas it is incorrect at the lower level). The activation energy for the boat was higher than that for the chair, however the calculated activation energies were very different to the experimental ones.
It was also possible to investigate the thermochemistry data at different temperatures using the FreqChk utility in Gaussian3. The corrections at 500K are shown as an example:

- ↑ Chemistry wiki Template:Www.ch.ic.ac.uk/wiki
- ↑ R. Pitzer, W. Lipscomb, J. Chem. Phys., 1963, 39, 1995. DOI:10.1063/1.1734572
- ↑ H. Rzepa,{{|http://vle.imperial.ac.uk/webct/cobaltMainFrame.dowebct}}
- ↑ B. Gung, Z. Zhu, R. Fouch, J. am. Chem. Soc., 1995, 117, 1783-1788. DOI:10.1021/ja00111a016
