Rep:Mod:jef15TS
Transition Structures
Introduction
Three pericyclic reactions were analysed with Gaussian, with a particular focus on the Diels-Alder reaction.
A transition structure is defined as a energy maximum on a certain reaction path way. This corresponds to a saddle point on the potential energy surface. Gaussian generates a PES and differentiates across the surface to find the saddle - the point at which force (first derivative of energy) is zero and the determinant of the Hessian matrix is negative.[1] This implies a single negative force constant which results in an imaginary frequency corresponding to the reaction coordinate.[1] The Intrinsic Reaction Coordinate (IRC) calculation locates the lowest energy pathway through this transition structure.
Nf710 (talk) 14:59, 15 December 2017 (UTC) You are being very brief. It doesn't differential across the surface. It differentiates wrt to each dimension of the PES which of the normal modes made up of linear combinations of the degrees of freedom. and it is the eigenvalues of the hessian. if the were 3 negative eigenvalues you would still get a negative determinant.
Two computational methods were used, PM6 and B3LYP. PM6 is semi-empirical method following the Hartree-Fock algorithm.[2] B3LYP is a hybrid functional applying density functional theory (DFT) and the Hartree-Fock method.[3] B3LYP was used with the 631G-(d) basis set.
Nf710 (talk) 14:59, 15 December 2017 (UTC) More detail would have been nice here.
Exercise 1: Diels-Alder Reaction between Butadiene and Ethene
(Fv611 (talk) Very well done on this section! Also well done on picking a nice pleasant color as a background for your MOs, and not something crazy like bright pink)
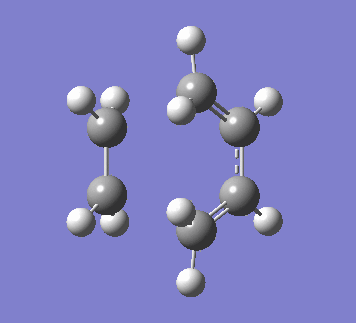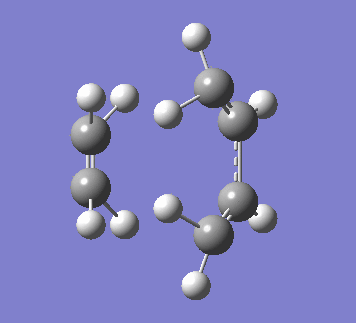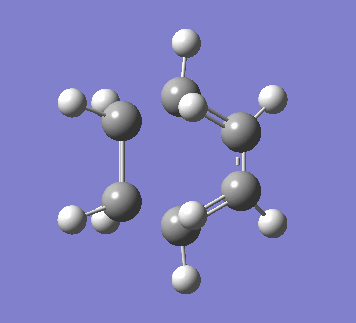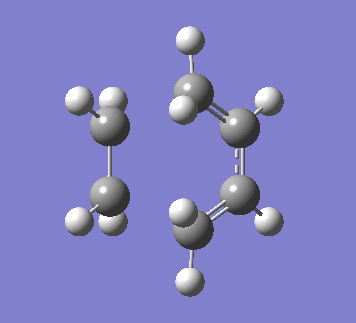
Butadiene and ethene can react in a [4+2] cycloaddition reaction, commonly known as a Diels-Alder reaction.
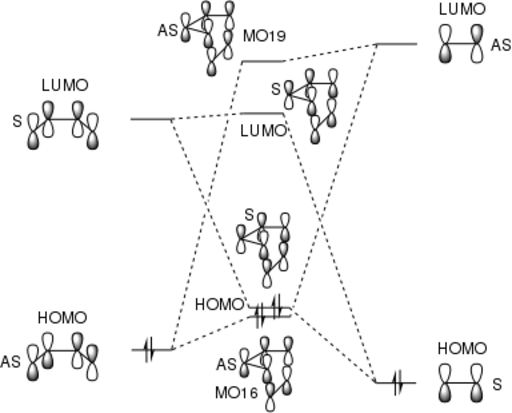
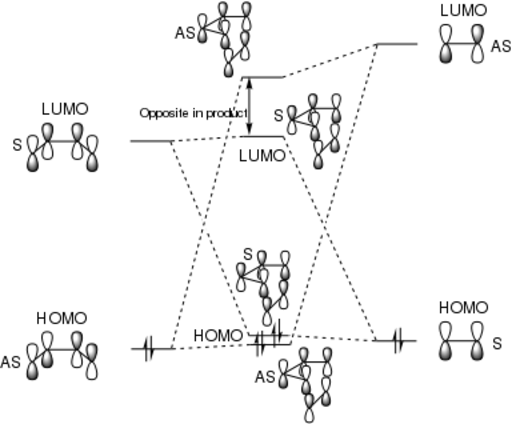
Below is an MO diagram for the Transition State of a Diels-Alder reaction between butadiene and ethene. The MOs pictured as Jmols below are labelled such that they match the MO diagram. It can be seen that the orbitals that combine in the TS are of the same symmetry. Molecular orbitals cannot be combined if they are of different symmetries.[4] The orbital overlap integral is zero for an antisymmetric-symmetric interaction and non-zero for a symmetric-symmetric/antisymmetric-antisymmetric interactions.[4] An AS-S interaction results in an AS term in the orbital overlap integral which integrates to zero over all space. AS-AS and S-S give symmetric terms which integrate to non-zero. [4]
|
|
|
|
|
|
|
|
The change in ‘bond length’ (in the reactants some are not strictly bonds) for the C-C ‘bonds’ involved in the Diels-Alder reaction are shown on the plot below. Bonds 3 and 5 are the bonds which form during the reaction, which is obvious since the bond length drastically shortens over the course of the reaction. Bonds 2, 4 and 6 are all double bonds in the reactants, since they are short at the start of the reaction. They all form single bonds, leading to an extension of the bond in the reaction. Bond 1 is a single bond, albeit conjugated so with some double bond character, which becomes the only double bond in the product. Therefore, it shortens and is the shortest C-C bond in the product. The computed bond lengths are shown in table 1 below.
| Length of bond / Å | ||||||
|---|---|---|---|---|---|---|
| Bond 1 | Bond 2 | Bond 3 | Bond 4 | Bond 5 | Bond 6 | |
| Reactants | 1.468 | 1.335 | 3.414 | 1.327 | 3.414 | 1.335 |
| Transition State | 1.411 | 1.380 | 2.114 | 1.382 | 2.115 | 1.380 |
| Products | 1.338 | 1.501 | 1.540 | 1.541 | 1.540 | 1.501 |
The average bond length for a sp³-sp³ C-C bond is 1.530 Å, sp²-sp² is 1.460 Å, sp²=sp² (double bond) is 1.316 Å and sp³-sp² is 1.507 Å.[5] The van der Waals radius for carbon is 1.70 Å.[6] In the reactants, bonds 2, 4 and 6 are clearly double bonds, although they are slightly longer than average due to conjugation (in butadiene) and their proximity (raising the energy of the system compared to if they were infinitely far away from each other). Bond 1 is a single bond between two sp² carbons but is slightly longer than typical due to the minimal conjugation in butadiene and the proximity of the two molecules. Bonds 3 and 5 are slightly more than twice the C-C van der Waals radius meaning there is no interaction between them.
In the transition state, the most notable change is that of bonds 3 and 5, which shorten significantly. They are significantly shorter than twice the van der Waals radius but still longer than a C-C single bond. Bonds 2, 4 and 6 are longer than in the reactants showing their transition from double to single bonds. Bond 1 is shorter, between the length of a single bond between two sp² carbons and a double C=C bond.
The products show that bond 1 is significantly shorter than the others and although being a double bond is longer than the typical length. This specific bond was measured physically to be 1.326 Å.[5] Bonds 2 and 6 are the same and are both single bonds adjacent to a double bond, this bond is very similar to the typical length. Bonds 3, 4 and 5 are all roughly the same length and are sp³-sp³ single bonds, although are slightly lower than the typical and the literature for cyclohexene (1.506 Å). They are also slightly longer than typical length but the very similar to the literature (1.541 Å). The discrepancies are likely to be due to the relatively low level at which the computation was done. A further optimisation at B3LYP with 6-31G(d) basis set was run and found that the bond lengths were different, with bond 1 decreasing to 1.337 Å, bonds 2 and 6 increasing to 1.510 Å, bonds 3 and 5 decrease to 1.537 Å and bond 4 decreased to 1.535 Å. These fluctuations demonstrate that the bond lengths are not fully optimised at PM6.
The vibration involved in the formation of the two bonds is shown below. The bonds form synchronously in a concerted reaction, as expected in a pericyclic reaction.
Other relevant files
PM6 Product: File:Jef15DAPROD.LOG
B3LYP Producy: File:Jef15DABLYP.LOG
IRC: File:Jef15DIELS-ALDER-IRC.LOG
Exercise 2: Cyclohexadiene and 1,3-Dioxole
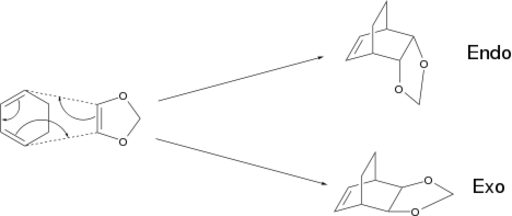
When the dienophile has substituents, there are two possible products. The endo product is given when the dienophile approaches with its substituents eclipsing the double bonds on the diene and the exo is given by the opposite approach.[7] The reaction studied is shown below, with both products.
This reaction is an inverse electron demand Diels-Alder reaction because the diene is less electron rich than the dienophile due to the presence of the oxygen in the dienophile.[7] Therefore the strongest interaction is now between the HOMO of the dienophile and the LUMO of the diene instead of the HOMO of the diene and LUMO of the dienophile as in Exercise 1. Although this does not affect the order of the MOs formed in the transition state, the two unoccupied orbitals shown are in the opposite order in the product due to the strong interaction of the dienophile HOMO and diene LUMO. The MO diagram is shown below, the rest of the molecules have been ignored to ensure the diagram is clear, secondary orbital interactions are discussed later.
(Fv611 (talk) Your MO diagram is good, but like Ana you should have discussed the difference between the endo and exo case, and labelled your MO diagram indicating which one is the diene and which one the dienophile. Additionally you should have labelled or numbered the TS MOs to relate them to your Jmol table.)
|
|
|
|
|
|
|
|
Below is a table showing the reaction energies and barriers for the Diels-Alder reaction between 1,3-cyclohexadiene and 1,3-dioxole. The energies were calculated at the B3LYP level.
| Reaction Barrier / Hartree per molecule | Reaction Barrier / kJ/mol | Reaction Energy / Hartree per molecule | Reaction Energy / kJ/mol | |
|---|---|---|---|---|
| Endo | 0.06036 | 158.48 | -0.026184 | -68.75 |
| Exo | 0.63339 | 166.30 | -0.02481 | -65.14 |
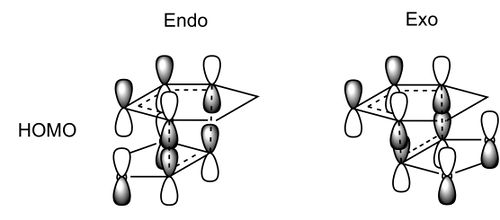
It can be seen that for the endo reaction, the reaction barrier and energy are lower meaning the endo product is preferred kinetically and thermodynamically over the exo product. There are secondary orbital interactions in the endo transition state which stabilise the transition state somewhat.[7] This can be seen in the HOMOs and bonding MOs below the HOMO (above) of each transition state. In the endo there is an overlap between p-orbitals on the oxygens in the dioxole and the back of the π system in cyclohexadiene. This overlap is not possible in the exo state. These interactions are shown to the right. The endo is also a lower energy product due to less steric clash. In the exo product there is some clash between the 5 membered ring and the protons on the sp³ carbons ‘bridging’ the 6 membered ring which is not present in the endo product.
Other relevant files
B3LYP 1,3-Dioxole: File:Jef15DIOXOLEBLYP.LOG
B3LYP Cyclohexadiene: File:Jef15CYCLOHEXADIENEBLYP.LOG
B3LYP Endo product: File:Jef15EX2ENDOPRODBLYP.LOG
B3LYP Exo product: File:Jef15EX2EXOPRODBLYP.LOG
Endo IRC (PM6): File:Jef15EX2ENDOIRC.LOG
Exo IRC (PM6): File:Jef15EX2EXOIRC.LOG
Nf710 (talk) 09:38, 18 December 2017 (UTC) This is good but quite brief and concise. You could have used a diagram to show the steric clashing. But it is interesting that you looked at the ordering of the MOs in the product too. Furthermore you could have gone into more detail in the theory for the intro.
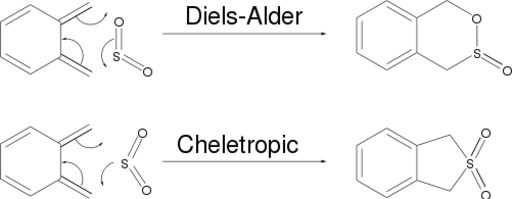
Exercise 3: Diels-Alder vs Cheletropic
o-Xylylene and sulfur dioxide can react in a Diels-Alder sense or differently - in a cheletropic reaction. The scheme below shows the difference between these mechanisms.
Below are animations of the three reactions.
| Cheletropic | Endo | Exo |
|---|---|---|
 |
 |
 |
| Reaction Barrier / Hartree per molecule | Reaction Barrier / kJ/mol | Reaction Energy / Hartree per molecule | Reaction Energy / kJ/mol | |
|---|---|---|---|---|
| Endo | 0.030996 | 81.38 | -0.03787 | -99.41 |
| Exo | 0.032513 | 85.36 | -0.03811 | -100.05 |
| Cheletropic | 0.039496 | 103.70 | -0.05957 | -156.39 |
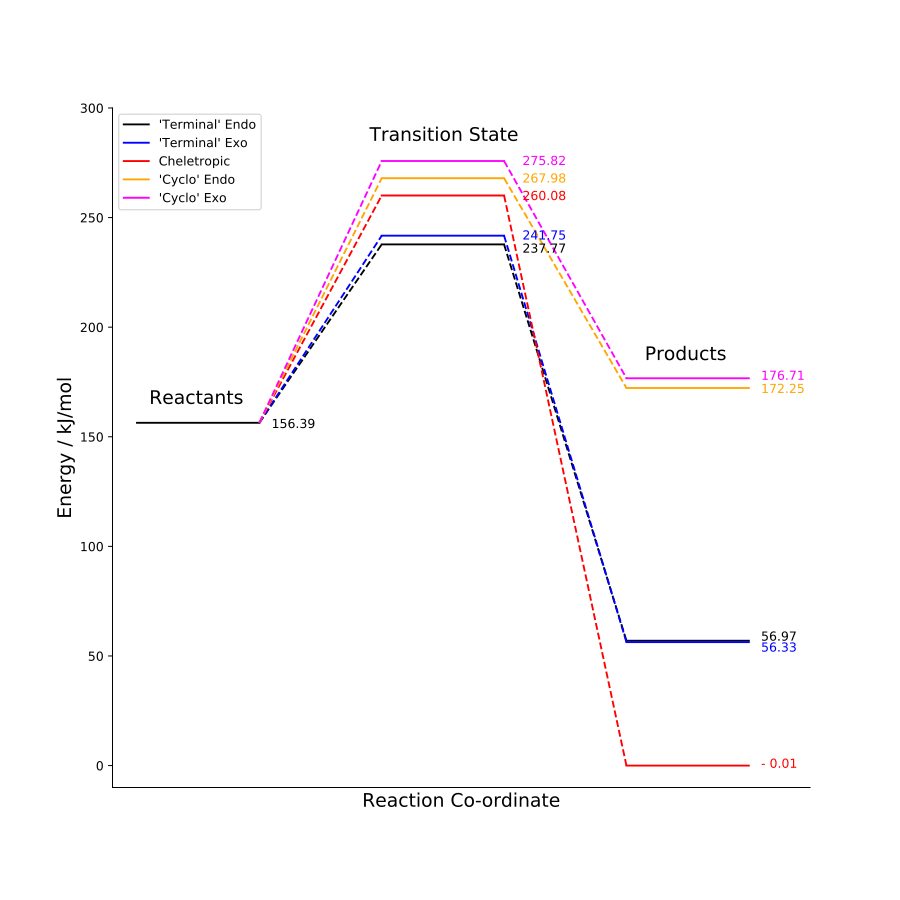
These results are displayed on a reaction energy profile below.
(Normalise the reaction profile to the reactants to make comparison easier. I appreciate the lack of Excel here Tam10 (talk) 15:12, 7 December 2017 (UTC))
The endo product is the kinetically preferred product because it has the lowest activation energy but the cheletropic product will be far more thermodynamically favourable because it has a much more negative reaction energy. All three reaction paths show a significant exothermic reaction energy, meaning the products are much lower in energy than the reactants. This is due to the formation of a very stable benzenoid ring which is not present in o-xylylene. This is clearly visible in the animations above.
In o-xylylene there are two positions in which a Diels-Alder reaction can take place. In the first part of this exercise only one position (the 'terminal' site) was considered. The alternative 'cyclohexadiene' site is shown in the scheme below.
The 'terminal' site is indeed the favourable site. The reaction barrier and energies are shown for the 'cyclohexadiene' site below.
| Reaction Barrier / Hartree per molecule | Reaction Barrier / kJ/mol | Reaction Energy / Hartree per molecule | Reaction Energy / kJ/mol | |
|---|---|---|---|---|
| Endo | 0.042505 | 111.60 | 0.006043 | 15.87 |
| Exo | 0.04549 | 119.43 | 0.007741 | 20.32 |
It can already be seen that this reaction is not favourable, given the positive reaction energies. However a graphical representation, comparing these reactions to those discussed earlier, shows this even more clearly.
Not only are these products of higher energy than the reactants but the transition state is also much higher in energy than any of the other paths. Therefore, these reaction paths are highly unfavourable. An obvious reason for the higher energy transition states and products is the lack of aromatic benzenoid ring in the product.
(Another reason is the deformation of the xylylene. Less energy is needed to sp3 hybridise the terminal carbons compared to the ring that has to adopt an unusual configuration Tam10 (talk) 15:12, 7 December 2017 (UTC))
Other relevant files
o-Xylylene: File:Jef15XYLYLENE.LOG
Sulphur dioxide: File:Jef15SO2.LOG
'Terminal' Endo Product: File:Jef15EX3DAENDOPROD.LOG
'Terminal' Endo IRC: File:Jef15EX3ENDOIRC.LOG
'Terminal' Endo Transition State: File:Jef15EX3ENDOTS2.LOG
'Terminal' Exo Product: File:Jef15EX3DAEXOPROD.LOG
'Terminal' Exo IRC: File:Jef15EX3DAEXOIRC.LOG
'Terminal' Exo Transition State: File:Jef15EX3EXOTS.LOG
Cheletropic Product: File:Jef15EX3CHELEPROD.LOG
Cheletropic IRC: File:Jef15EX3CHELEIRC.LOG
Cheletropic Transition State: File:Jef15EX3CHELETS.LOG
'Cyclohexadiene' Endo Product: File:Jef15EX3EXTENDOPROD.LOG
'Cyclohexadiene' Endo IRC: File:Jef15EX3ENDOIRC.LOG
'Cyclohexadiene' Endo Transition State: File:Jef15EX3EXTENDOTS.LOG
'Cyclohexadiene' Exo Product: File:Jef15EX3EXTEXOPROD.LOG
'Cyclohexadiene' Exo IRC: File:Jef15EX3EXTEXOIRC.LOG
'Cyclohexadiene' Exo Transition State: File:Jef15EX3EXTEXOTS.LOG
Conclusion
All of the results obtained agree with theory, namely the endo rule, suggesting that computations of this type are a valid alternative to 'classical' experiment. The results of exercise 3 are particularly relevant in this sense since o-xylylene is highly reactive, making 'classical' experiment technically difficult.[8] However, this computational method allows calculation of the reaction barriers and energies for the reaction with sulfur dioxide far more easily than could be achieved with physical experiment, if even possible. These methods were performed on relatively simple molecules. Further work on more complex systems is required to truly test the capabilities of this method.
References
- ↑ 1.0 1.1 Gaussian – Vibration Analysis in Gaussian, http://gaussian.com/vib, (accessed December 2017)
- ↑ Gaussian – Semi-Empirical Methods, http://gaussian.com/semiempirical, (accessed December 2017)
- ↑ Gaussian – Density Functional (DFT) Methods, http://gaussian.com/dft, (accessed December 2017)
- ↑ 4.0 4.1 4.2 P. Atkins, T. Overton, J. Rourke, M. Weller and F. Armstrong, Shriver & Atkins’ Inorganic Chemistry, Oxford University Press, 5th edn., 2010.
- ↑ 5.0 5.1 A. G. Orpen, L. Brammer, F. H. Allen, O. Kennard, D. G. Watson and R. Taylor, J. Chem. Soc. Dalt. Trans., 1987, S1–S83.
- ↑ F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry Part A: Structure and Mechanisms, 2007.
- ↑ 7.0 7.1 7.2 J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, 2nd edn., 2012.
- ↑ R. D. Miller, J. Kolc and J. Michl, J. Am. Chem. Soc., 1976, 98, 8510–8514.