Rep:Mod:jd2615TS
Computational methods to determining transition states
Introduction
The potential energy surface (PES) is useful representation of the many different energy states a particular species can exist in. It provides a mathematical relationship between's a molecules energy and it's structure. [1]. It can be extremely useful for computational chemists as it provides mathematical meaning for a molecules structure, while also providing a 'framework' for programmers to design a code which can accurately determine the energy of a species. [1]. With peaks being transition species and troughs being intermediates or products, the mathematical landscape of a three-dimensional PES provides a visual justification for the products formed in the synthesis lab and will hopefully shed light on the different species encountered in the experiment.
The Diels-Alder reaction has been a prominent synthetic tool for chemists for many years. The understanding of the nature of the diene and the dienophile has been the source of interest for both synthetic and computational chemists, providing more opportunity for electrocyclic chemistry and better correlation between synthetic results and molecular interactions. This experiment investigates the interaction between different dienes and dienophiles, focussing primarily on the orbital formations of the transition state by the use of computational techniques. Through the variety of reactants, this experiment hopes to shed light on the precise mechanistic dynamic by providing energies, bond distances and orbital conformations. Work by Domingo [2] showed that the DFT methods at the B3LYP/6-31G level could be used to determine a reaction model for an ionic Diels-Alder reaction by the investigation of the oxa-Povarov reaction which is initialized by the ionic Diels-Alder of a cationic aryl oxonium and an alkene.[2] They determined, through the analysis of the IRC, that the substituents on the alkene (i.e. the phenyl ring on phenyl ethylene) forced a two-step mechanism, as opposed to the usual concerted one step approach.[2] Further work by Black [3] (computed by UB3LYP/6-31(G)) into the dynamics of bond formation of the Diels-Alder reaction observed that regardless of the symmetry of the reactants, the trajectories of bond formation are unequal in the transition state, but they concluded that at room temperature, due to shorter time gap of the formation of two new bonds compared to the C-C bond vibrational period, the Diels-Alder are concerted and stereospecific.[3]
Computation Techniques
In computational chemistry, there will be range of understanding of the structure a chemist is trying to identify. Different degrees of understanding require different techniques depending on whether an individual knows what their seeking. There are three methods for locating transition states with Gaussian:
Method 1: This method requires a good understanding of the transition state of a particular reaction. Here the chemist forms the starting materials in an arrangement which resembles the transition state of the reaction, the structure is optimized to a transition state that hopefully resembles natural state. The chemist must have a good understanding of bond angles and distances in order to accurately recreate the structure they are looking for.
Method 2: This method is more advanced than method one and still requires a knowledge of the transition state, but it is the fastest reliable method. Here the chemist draws the transition state from starting material according to their understanding of the structure. Then the bonds are frozen between the starting materials using Redundant Coordinate Editor. The structure is then optimised to a minimum with the frozen bonds so that the functional groups of the reacting molecules arrive at the most stable position. The minimised structure is then unfrozen and allowed to be minimised to a transition state that should resemble the natural state.
Method 3: This method requires more steps than method 1 or 2, but requires little knowledge of the transition state. Here the product is drawn and optimized to a minimum. The minimized product is then separated into the reacting fragments by breaking the bonds between them (i.e. separating the product into the two reactants). The reactant fragments are then separated slightly and frozen using redundant coordinates. The frozen structure is then optimized to a minimum, which is then optimized to a transition state.
The Hartree-Fock method is a set of equations which provide the best one-electron wave functions approximations to the problem of an electron in the motion of a field of atomic nuclei.[4] The description of the relationship of an electron within the potential of the nuclei can provide an approximation for a structure of a molecular state. b3lyp calculations calculate electron distributions with the use of Density Functional Theory (DFT) which is when the electrons are described in accordance to their density and not individual wave functions, its a progression on from the Hartree-Fock method. The energy of a system can be separated into six components:
Where NN is nuclear-nuclear repulsion, v is attraction, coul is electron-electron Coulombic repulsion, T is kinetic energy of electrons, exch is the electron-electron exchange energy and corr describes the correlated movement of electrons of different spin. [5].
The The majority of these experiments will use the semi-empirical quantum chemistry method with are based on Hartree-Fock or DFT theory but also through application of approximate assumptions thus obtaining empirical data. [6]. When molecules are very large, the use of semi-empirical over full Hartree-Fock as the whole calculation is less expensive. [6]. One exercise in this experiment makes of b3lyp which
Nf710 (talk) 09:31, 17 April 2018 (BST) You have shown a good brief understanding of the computational methods. But in this section you should have shown a good understanding of how we navigate a PES and how we used the Hessian matrix to find the force constants of the various normal modes.
Exercise 1
(Fv611 (talk) Excellent work across the whole exercise. Great job!)
Computational Method
The starting materials were optimized to a minimum using semi-empirical PM6. The product was also optimized using this technique. Once the product was optimized, the bonds between the alkene and the diene were removed, moved slightly apart but still within the Van der Waals radius, and frozen using redundant coordinates. This structure was optimized to a miniumum using semi-empirical PM6 to minimise a transition state-like structure. The minimised structure was then optimised to a transition state (Berny) where the force constants were calculated once using semi-empirical PM6.
Reaction Scheme
This experiment saw the Diels-Alder simulation between butadiene and ethylene to give cyclohexene:
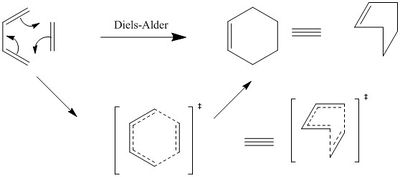 |
The Diels-Alder reaction sees a [4+2] cycloaddition of a conjugated diene and an alkene dieneophile via the interaction of 4 pi electrons from the diene and 2 pi electrons from the alkene, where the driving force is provided by the more stable sigma bond formed between the reactants, when compared to the weaker pi bonds.
MO diagram
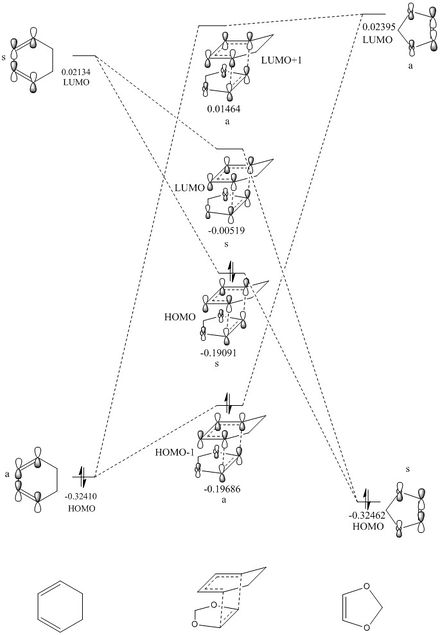
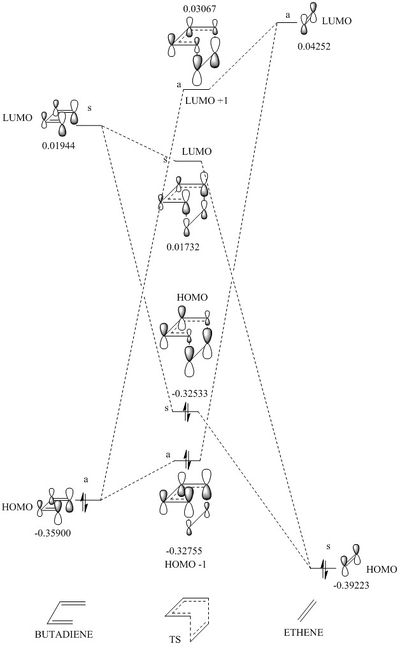 |
The transition state is given by the linear combination of the fragment HOMO-LUMO orbitals of both the butadiene and the ethylene. The orbitals are combined according to symmetry, where the symmetry is labelled with a small s (symmetric) or a (asymmetric) next to the energy level of the orbital being described. Only orbitals of the same symmetry can combine. The differing degrees of contribution are represented by the size of the orbitals within the formed MOs, where larger contributions due to the similar relative energy of the source fragment is shown as a larger orbital. For example, the HOMO -1 orbital has a larger orbital contribution from the HOMO of the butadiene (as this is closer in energy), thus is shown as larger orbitals. From the law of conservation of orbital number, 4 molecular orbitals are formed from 2 fragment orbitals from each reactant. The orbitals calculated using gaussview are represented by the jmol images below. The HOMO -1 (i.e. lowest energy) is formed from the two asymmetric fragments of the frontier orbitals. When comparing the calculated HOMO MOs, there is greater bonding character for the HOMO-1 relative to the HOMO, resulting in a more stable electronic distribution. The same reason applies to the LUMOs, where the LUMO +1 sees the greatest antibonding character thus being highest in energy.
Jmol of orbitals
|
|
|
|
|
|
|
|
Analysis of direct linear combination of orbitals of different symmetry shows that the orbital overlap integral is zero:
 |
Both orbital MOs formed in the above diagram would have zero overlap integral as one p orbital from the alkene forms a bonding interaction whereas the other is anti-bonding. If this system saw a break of symmetry, then the integral will become non-zero and bonding interactions will occur.
Bond Distances
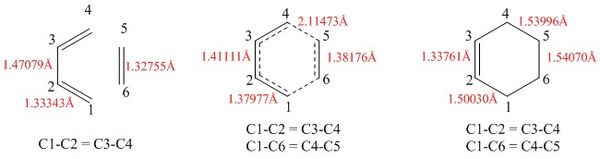 |
The above figure shows the bond lengths of the various bonds of the reactants, transition state (TS) and products respectively. Firstly, the ethylene reactant sees a standard sp2 double bond length of 1.32755Å (C5-C6). Mechanistically, the pi electrons of the ethylene form one of the sigma bonds to the butadiene during the concerted electrocyclic process, thus forming an sp3 single bond in the product (C5-C6 = 1.54070Å) (the other sigma bond to the ethylene is formed from pi electrons on the butadiene). The bond lengths confirm this observation as the transitions state sees a single-double intermediate bond length of 1.38176Å. The same process occurs for the C3-C4 and C1-C2 which change from double to single bond with an intermediate bond length (C1-C2 (reactants) = 1.47079Å, C1-C2 (transition state) = 1.37977Å, C1-C2 (products) = 1.33761Å). The opposite process occurs for the C2-C3 where it is originally a single bond in butadiene (C2-C3 = 1.47079Å), which is slightly shorter than a normal sp3 single bond, which is a result of the conjugation between the alkenes resulting in a small degree of double bond character. The bond length shortens as it becomes a double to 1.41111Å in the transition state and 1.33761Å in the product. The C1-C6/C4-C5 bond length in the transition state is 2.11473Å. The Van der Waals radius of carbon is around 1.5Å, thus any carbon-carbon distance that is less than 3Å can constitute a bond, thus the bond length of the C1-C6 allows for the formation of the bond. This bond length shortens to 1.53996Å as a single bond forms.
The JSmol represents the vibration that forms the bond during the transition state. It is evident from the image that C2-C3 shortens as the ethylene and the butadiene approach. The symmetrical motion of this vibration and the equality of C4-C5/ C1-C6 bond lengths provides confidence to conclude that the formation of the two sigma bonds between the ethylene and the butadiene are synchronous.
IRC analysis
 |
 |
The top IRC represents the conversion of the reactants to the products (right to left) via the high energy transition state. The bottom plot shows the first derivative of the top IRC plot, thus representing the change in gradient. The key features of the bottom plot include a starting gradient roughly equal to 0, then an increase in gradient as the energy barrier is overcome, then a drop to zero at the transition state. The IRC animation reiterates the synchronous nature of the formation of cyclohexene via a Diels-Alder reaction.
Log Files
Exercise 2
Computational Methods
For each reaction (ENDO or EXO), the starting materials were optimised to a minimum using DFT b3lyp/6-31G(d). The product was also optimized using this technique. Once the product was optimized, the bonds between the cyclohexadiene and the dixole were removed, moved slightly apart but still within the Van der Waals radius, and frozen using redundant coordinates. This structure was optimized to a minimum using DFT b3lyp/6-31G(d) to provide a minimised transition state-like structure. The bonds were unfrozen and the minimised structure was then optimised to a transition state (Berny) where the force constants were calculated once using DFT b3lyp/6-31G(d).
Reaction Scheme
This experiment saw the Diels-Alder reaction of cyclohexadiene and dioxole. The main variation in this reaction compared to butadiene and ethylene is that the approach of dienophile can result in two different products, endo and exo:
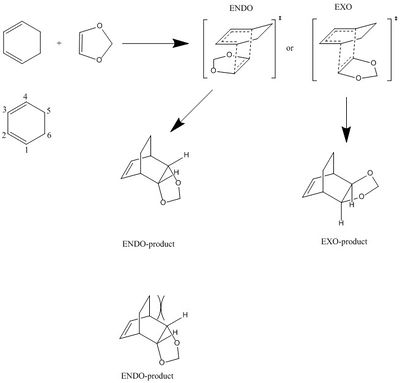 |
Here the two different products are a result of the different conformations of the transitions state. The ENDO-product has the dioxole pointing in the direction of the diene, whereas the EXO-product points away from the diene. The endo product is the kinetic product (i.e. higher energy product confirmation and lower energy transition state), whereas the EXO product is usually the thermodynamic product (i.e. lower energy product and higher energy transition state) but this is not the case for this reaction. From the analysis of the MO diagram, the stabilised transition state of the ENDO-product is a result of the p orbitals on the oxygen of the diaxole interacting with the p orbitals on carbon 2 and 3 of the cyclohexadiene, thus reducing the energy of the state. As the dioxole points away in the exo product, this particular orbital interaction does not occur, and the transition state is higher in energy. The ENDO-product is usually higher in energy as the protons, which ‘stick up’, are in steric clash with the carbon bridge (see figure 2).
MO diagrams
(Fv611 (talk) Again, lovely MO diagrams.)
The difference in endo and exo states are rationalized again by the direction of the dienophile with respect to the diene. In the exo product, it is evident that the p orbitals on the oxygen of the dienophile are not involved by stabalisation of the state. The following image shows the secondary interaction which leads to the stabilization of the ENDO state:
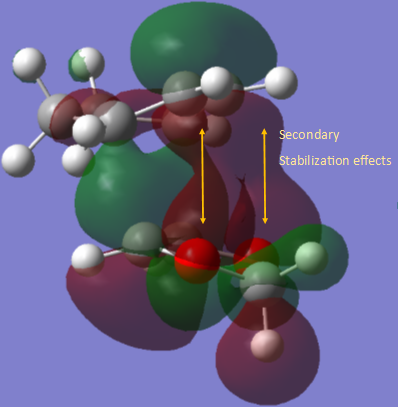 |
It is possible to rationalise the orbitals calculated by comparing their structure to the orbital combinations in the MO diagram. The 4 MO’s in the diagram in ascending order are the LUMO -1, LUMO, HOMO and HOMO +1. An important feature to notice in the calculated MOs is the stabalising effects as a result of the interaction between the p orbital on the oxygens of dioxole and the p orbitals of the 2-3 carbon atoms on the diene (illustrated with the yellow arrow). The HOMO shows some stabilisation from the interaction of the p orbitals on the 2,3 carbons on the butadiene and the alkene p orbitals on the dioxole.
In order to determine the nature of the Diels-Alder, it is necessary to look at the electronics of the reactants. The normal electron demand Diels-Alder sees an electron rich diene and an electron poor dienophile. Cyclohexadiene is neither electron rich or poor in this example. However, the lone pair on the oxygen of diaxole readily feeds electron density onto the alkene, thus deeming it electron rich:
 |
This different electron destribution in the dienohphile means that the HOMO of the dienophile is higher in energy than the HOMO of the diene, which is characterisitic of an inverse demand Diels-Alder reaction.
Energy Calculations
| Energy / Hartrees | |
|---|---|
| Cyclohexadiene | --233.324 |
| Dioxole | -267.068 |
| Reactant total | --500.393 |
| ENDO-product | -500.419 |
| ENDO Transition State | -500.351 |
| EXO-product | -500.417 |
| EXO Transition State | -500.329 |
As expected, the total energy of the reactants is higher than the individual products. When comparing the energy of the transition states, the endo product is lower than the exo product, which contradicts previous hypothesis that the steric clash with the protons will increase the energy in the ENDO product. It is expected that potential steric clash between the dioxole group and the bridging group in the EXO product results in higher energy. The ENDO energy barrier calculated from the difference in energy from the reactants to the ENDO transition state is 0.0420 Hartrees. The EXO energy barrier calculated via the same technique was 0.033 Hartrees, showing that the EXO TS is higher in energy than the ENDO TS.
Nf710 (talk) 09:41, 17 April 2018 (BST) You should have worked this out in KJmol-1. Furthermore in your discussion your numbers say that your endo barrier is higher than the exo. But then you say that the exo is higher.
Jmol images
|
|
|
|
|
|
|
|
|
|
|
|
Thermodynamics
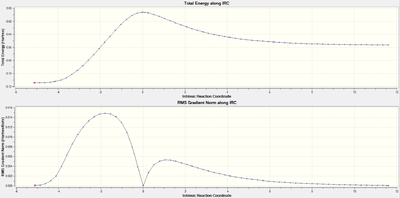 |
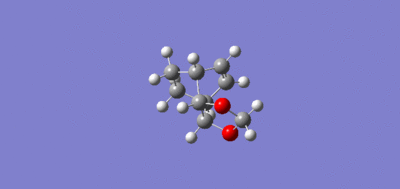 |
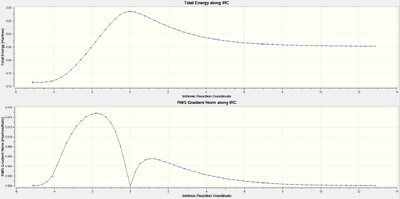 |
 |
Both IRC pathways show a similar pattern. The top plot of both IRC’s is the actual energy along the reaction coordinate, where the peak corresponds to the energy of the transition state. The left side is the lower energy of the products, which is the result of the more stable sigma bond in comparison to the higher energy pi bonds of the reactants which are displayed on the right side. The lower plot IRC is the gradient along the reaction coordinate. The point where the gradient drops to zero corresponds to the transition (where the first derivative of the plot is zero.) The single peak of the IRC shows that the reaction occurs with one step, reflecting the concerted nature of the Diels-Alder, as two sigma bonds are formed simultaneously.
Nf710 (talk) 09:57, 17 April 2018 (BST) This section was good. Your discussion and conclusions were good. And you backed up your ideas with very nice diagrams. Your evaluation of the numbers let you down. And there was no quantitative analysis of the electron demand of this reaction. Arrow pushing is not sufficient in computational chemistry.
Log Files
Exercise 3
Computational methods
For each reaction in this exercise, the starting materials were optimized to a minimum using semi-empirical PM6. The products were also optimized using this technique. Once the product was optimized, the bonds between the Xylylene and the sulfer dioxide were removed, moved slightly apart but still within the Van der Waals radius, and frozen using redundant coordinates. This structure was optimized to a miniumum using semi-empirical PM6 to minimise a transition state-like structure. The minimised structure was then optimised to a transition state (Berny) where the force constants were calculated once using semi-empirical PM6.
Reaction Scheme
This experiment investigates the Diels-Alder reaction between o-Xylylene and Sulpher Dioxide. Unlike other Diels-Alder reaction, this reaction can go via a Chelotropic reaction which is a form of pericyclic reaction where, unlike the traditional Diels-Alder, both new bonds to the dienophile occur on a single atom (i.e. the Sulfer atom). This exercise seeks to rationalise which of the three potential products from this reaction could be the most stable.
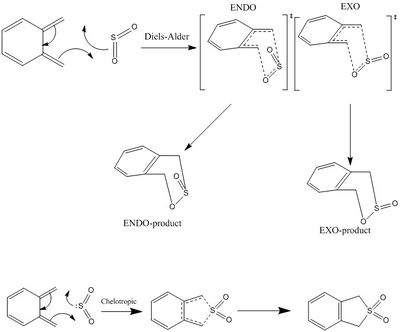 |
The mechanism for the Cheletropic pericyclic reaction is a product of the sulfer being both electrophilic and nucleophilic, where the lone pair on the sulfer attacks the o-Xylylene.
 |
 |
 |
 |
 |
 |
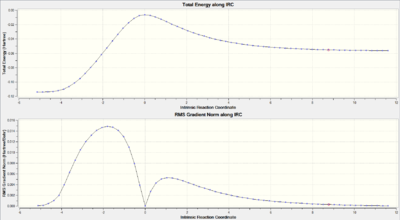
The IRC for all these reactions shows that the energy barrier is very low. This can be rationalised by looking at the electronic structure of the six membered ring. The reaction results in formation of a stable aromatic benzene ring which is a lot more stable than the diene structure before, this results in a low activation and a much more stable product.
Thermodynamics and kinetics of reaction
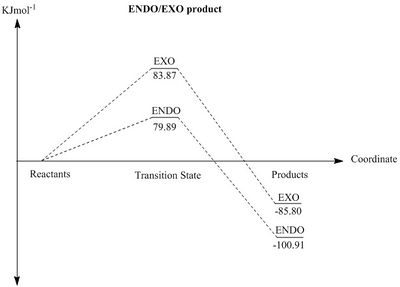
From analysis of the thermochemistry extracted from the data produced by the calculation, it is evident that the thermodynamic product is the cheletropic product.
 |
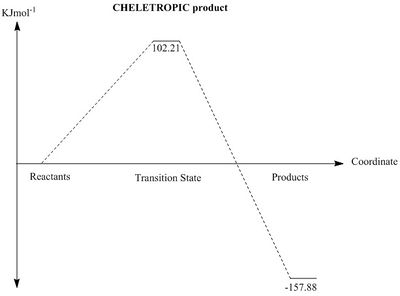 |
The above plots show the relative energies of each species during the reaction of o-Xylylene and sulfer dioxide. From the calculated energies, the Cheletropic product is the thermodynamic product as a result of the more stable 5-membered ring, but it shows a large transition state energy, whereas both Diels-Alder products are the kinetic products. As with all Diels-Alder mechanisms, the kinetic stability of the endo transition state is a result of the interaction of the pi bond from the non-reacting S-O bond interacting with the p orbitals of the diene, as this S-O bond sits in the correct geometry. The non-reacting S-O bond points away from the diene, thus preventing any pi-p secondary interactions. There are no secondary orbital interactions for the cheletropic reaction, so that results in a higher energy transition state. When comparing the transition states for the Diels-Alder and Cheletropic, the six membered transition state shows less ring strain, thus causing stabilisation. The 5 membered transition state has greater ring strain, so is higher in energy.
Work by Jose Sordo [7] showed that during this mechanism, an external sulfer dioxide group is involved in the stability of the transition state and also provides an energy compensation for the free energy loss as a result of the decrease in entropy as two molecules form one.[7]
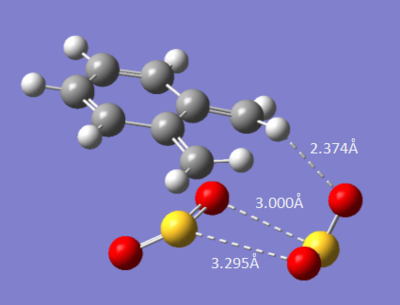 |
The image above shows the conformation of the accessory sulfer dioxide, where the dashed lines represent the stabalising interaction. A further calculation was set up to determine if the Sulpher dioxide had a stabilization effect on the transition state. In the literature it states that an MP2/6-31G calculation was set up, however a b3lyp/6-31G(d) calculation was used.[7] The amount of time it took for the calculation to complete meant that it was impractical to run to completion. The transition state with frozen bonds was successfully calculated. However; the optimization to transition state (Berny) took too long to optimize, but the following intermediate structures were formed, below:
 |
From visual analysis, the calculation passes the previous transition state, bonding the Sulfer dioxide and diene together. The accessory sulfer dioxide remains in the same place, just changing it's orientation with respect to the conformation of the main molecule. However, if the position of the extra molecule was very unfavorable, it would rapidly change it's position, either towards or away from the Diels-Alder product. This observation suggests that the position of this molecule is relatively stable, however further experiment would be required with more time and computing power. The result of this experiment also suggests that the b3lyp may be inadequate for this type of calculation, so further experiments would require the reproduction of the literature method by using MP2/6-31G.[7]
(Unfortunately MP2/6-31g(d) is also inadequate for this type of calculation. The gradient will be extremely small when looking at non-bonding interactions, making optimisations very difficult as you found above Tam10 (talk) 15:27, 4 April 2018 (BST))
Other potential Diels-Alder reactions
The ENDO-site Diels-Alder reaction is as follows:
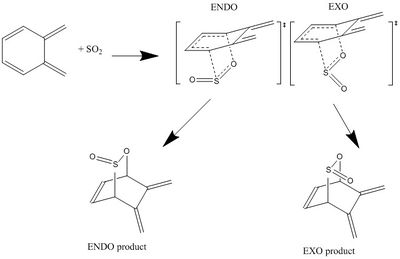 |
Here the Sulfer dioxide reacts with the diene that is constituent of the six membrered ring. As with most Diels-Alder reactions, this reaction can either be ENDO or EXO with respect to the position of the non-reacting sulfer-oxygen bond.
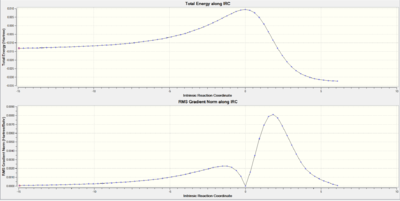 |
 |
 |
 |
The above IRCs represent the reaction coordinate of this reaction of Sulpher dioxide at this particular site of the diene. From analysis of this, the transition state and the product formed will be higher in energy because neither species are aromatic, unlike the reaction on the EXO-site (outside the 6 membered ring) of the molecule. The absence of aromaticity means the molecule is less stable compared to the EXO product.
| Transition State / kJ/mol | Product / kJ/mol | |
|---|---|---|
| ENDO | 267.98 | 172.25 |
| EXO | 275.82 | 176.68 |
The lack of aromaticity of the transition state and the products is reflected in much higher energy values when compared to the EXO-site compounds. Again, the ENDO transition state is lower than the EXO because of the secondary p-pi orbital interaction between the oxygen on the alkene and the and pi orbitals of the diene (mentioned in previous sections).
Log Files
EXO-SITE ENDO TRANSITION STATE
ENDO-SITE EXO TRANSITION STATE
ENDO-SITE ENDO TRANSITION STATE
Extension Log files: Failed to converge
Extension with accessory sulfer dioxide molecule
Extension
Computational methods
The product was optimized to a minimum using semi-empirical PM6. The length of the sigma bond formed during the reaction was increased and the bond was removed, where the new positions are frozen using redundant coordinates. This structure was optimized to a miniumum using semi-empirical PM6 to minimise a transition state-like structure. The minimised structure was then optimised to a transition state (Berny) where the force constants were calculated once using semi-empirical PM6.
Hypothesized reaction
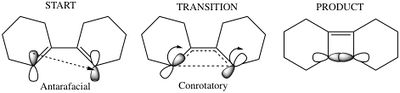
Electrocyclic reactions can be distinguished according to whether they are conrotatory or disrotatory. Huckel theory describes the requirements for thermal and photochemical electrocyclic ring closures. The following reaction is being investigated to determine it's reaction coordinate and the orbital dynamics of the transition state:
 |
For a thermal reaction with 4 pi electrons, Huckel theory states that if the reaction is to proceed via a Huckel transition state, the sigma bond forms via disrotatory motion of the p orbitals at the end of the diene which are in an antarafacial arrangement:
(Not Hückel theory. Also, it would undergo conrotation Tam10 (talk) 15:34, 4 April 2018 (BST))
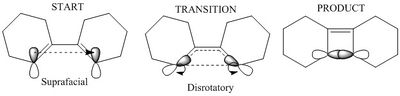 |
The transition state and IRC was optimised using PM6, semi empirical method. The following transition state was optimised which provided the transition state vibration represented with the negative frequency:
(This is conrotation Tam10 (talk) 15:34, 4 April 2018 (BST))
IRC Calculation
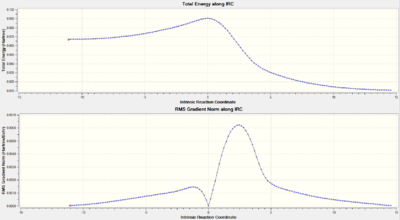 |
 |
|
|
|
|
The orbital of interest in the transition state is the LUMO. the twist in the molecular orbitals of the state result in a mobius aromaticity where molecular orbital follows the topology of a mobius strip, thus Huckel theory cannot be used to describe this species. In a mobius transition state, a thermal 4 electron system is antarafacial, conrotatory [8]:
 |
 |
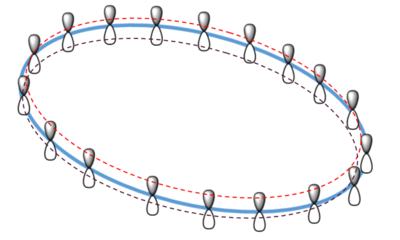 |
The above figure represents the mobius topology where each p orbital has a slight rotation when compared to it's adjacent partner, resulting in an aromatity that forms a loop with a half twist, unlike the huckle aromatic transitions state that shows no twist, just two symmetrical planes.[8] This diene complex undergoes the same principle where the pi-p orbitals involved in the butadiene undergo a disrotatory twist where the resulting transition state has mobius aromaticity, which is thermally allowed according to rules outlined in a publication by Henry S Rzepa which stated that a 4 pi pericyclic reaction can occur thermally as long as the p orbital arrangement forms a stable mobius aromatic species.[8] Further work in Henry S Rzepa's publication outlined interesting comparisons between the mobius and Huckel aromaticity, one being that the ideal mobius strip has only C2 symmetry, thus the absence of further symmetry means the mobius aromatic transition has a non-superimposible mirror image, unlike the Huckel which has a superimposible mirror image.[8]
Log Files
Conclusion
This experiment has attempted to rationalise the synthetic difference in yield by describing orbital interactions and their energies with the use of computational techniques. Exercise one saw the most basic Diels-Alder reaction of butadiene and ethylene. This experiment was useful in determining the standard MO diagram for this reaction, showing the primary interactions without any influence from functionality of the different reactants with no secondary interactions forming ENDO or EXO products. It showed the importance of symmetry of the interacting orbitals, where only orbitals of the same symmetry interact, and different symmetry orbital interactions lead to an overlap integral of zero.
The second experiment introduced functionality to the starting materials by reacting 1,3-dioxole and cyclohexadiene. This experiment showed how position of the dienophile with respect to the diene results in different products formed through secondary interactions. The ENDO product always has a lower energy transition state as the p orbitals of the oxygen on the dienophile interacts with the p orbitals on C2 and C3 of the diene (See 'bond distances' in 'Exercise 1'), causing a stabalising interaction. Further consequences of the oxygen in the dienophile is that it feeds electron density into the alkene which results in an inverse Diels-Alder reaction, where the HOMO of the dienophile is lower than HOMO of the diene.
The third experiment introduced a non-carbon based dienophile to undergo a hetero Diels-Alder reaction. Firstly the EXO site (non-carbon ring diene) of the molecule was explored. Other than both the ENDO and EXO product, this reaction saw the cheletropic reaction where the sulfer atom reacts as both the nucleophile and electrophile, where both new sigma bonds are formed on the same atom (i.e. the sulfer atom). This experiment showed that the cheletropic reaction formed the thermodynamic product as a result of the more stable 5 membered ring structure, while showing the highest transition state energy due to increased ring strain of the transitions species. Further experiments were undertaken to investigate the effects of an accessory sulfer dioxide molecule on the transition state energy (experiment inspired by literature). This experiment was inconclusive as the transition state failed to converge. Further work could could be done with more time and computing power conclude this experiment. The ENDO site (carbon ring diene) was then investigated. This showed that the transition state energy and the product energy were much higher than those of the ENDO-site products. This was a result of the lack of aromaticity of the TS and products, thus being less stable and higher energy.
The extension exercise explored the electrocyclic ring closure of a diene under thermal conditions. It was expected that the reaction coordinate would proceed via a disrotatory motion of the diene's p orbitals to form a sigma bond between the end of the diene, where the transition state was stabalised by the symmetrical huckel aromaticity. However, from analysis of the HOMO orbitals of the TS, the state was stabalised by a mobius loop aromaticity formed through the slight rotation of p orbitals with respect to it's adjacent partner, resulting in a conjugation with a mobius topology. For a mobius transition state with 4n pi electrons, the reaction must proceed via a conrotatory motion of the p orbitals to form a sigma bond between the end of the diene.
Computation techniques have proven effective at representing these structures. However in the light of the extension where an accessory sulfer dioxide molecule can have an influence on the stability of a transition state, it is felt that further experiments need to be done including many molecule systems before a fair comparison between computed energies and synthetic yield can be correlated.
References
- ↑ 1.0 1.1 E.G. Lewars, Computational Chemistry, Springer, 2nd edn, 2011, ch 2, pg 9
- ↑ 2.0 2.1 2.2 Luis. R Domingo, The mechanism of ionic Diels–Alder reactions. A DFT study of the oxa-Povarov, RSC Adv, 2014, 4
- ↑ 3.0 3.1 K. Black, Dynamics, transition states, and timing of bond formation in Diels–Alder reactions, PNAS, 2012, 12860-12865
- ↑ J. C. Slater, A simplification of the Hartree-Fock Method, Physical Review, 1950, 81, 3, 385-386
- ↑ 5.0 5.1 Michael Filatov, Assessment of Density Functional Theory for Describing the Correlation Effects on the Ground and Excited State Potential Energy Surfaces of a Retinal Chromophore Model, J. Them. Theory Comput., 2013, 9, 3197-3932
- ↑ 6.0 6.1 Jan Řezáč, Semiempirical Quantum Chemical PM6 Method Augmented by Dispersion and H-Bonding Correction Terms Reliably Describes Various Types of Noncovalent Complexes, J. Chem. Theory Comput., 2009, 5 , 1749–1760
- ↑ 7.0 7.1 7.2 7.3 7.4 Jose A. Sordo, Sulfer Dioxide Promotes Its hetero-Diels-Alder and Cheletropic Additions to 1,2-Dimethylidenecyclohexane, J. Am. Chem. Soc, 1998, 120, 13276-13277
- ↑ 8.0 8.1 8.2 8.3 Henry S. Rzepa The Aromaticity of Pericyclic Reaction Transition States, J. Chem. Educ., 2007, 84, 1535