Rep:Mod:jd2613

Introduction

The transition state of a reaction is the point at which a certain geometry causes a maximum potential energy, over the complete reaction coordinate. From this point the reaction could progress in either direction, like a ball on the maximum of a hill could fall either way. The transition state can return to reactants or progress to products. Transitions states are defined due to having maximum potential energy and therefore all transition states are unstable and cannot be experimentally isolated. Through calculations, associated with potential energy surfaces, transition state geometries can be determined along with transition state energies. Using Hammond-Leffler Postulate an approximation can be made to determine whether the transition state is a late or early transition state, resembling the reactants or products of the reaction. To further this approximation computational calculations can be completed to determine a precise geometry and energy.

Within this experiment Gaussian was used to complete all optimization and frequency calculations and GaussView was used as a pre- and post-processor to determine geometries and set up reagents for the reaction, and to determine the outcomes of the calculations done by Gaussian. Three methods were used in this experiment,HF hartree fock , DFT and AM1.

Hartree-fock^[1] is a method of simply solving the electronic Schrodinger equation to produce an electronic wavefunction which is related to the potential energy surface.^[2]Simplifications of the electron interactions are made assuming an average potential experienced by all electrons, this is a poor description but results in an appropriate level of accuracy for this experiment.

DFT, density functional theory uses the Bohn-Oppenheimer approximation to reduce the number of degrees of freedom. Unlike Hartree-Fock theory which uses the electronic wavefunction, DFT deals with the electron density. From the electron density the total ground state energy of the system can be found.^[3]

AM1 is a semiempirical method which is a simplified version of the Hartree-Fock theory but with experimental based alterations in order to improve efficiency^[4]

There are also two GaussView input methods the first method, the guess method is loosely based around Hammond-Leffler postulate, and the second method is a synchronous transit-guided quasi-newton^[5] (QST) method. Although there is no method that can ensure that the correct transition state will be found.^[6]

Guess method,the reagents are arranged in a predicted geometry post-calculation due to either late or early transition state prediction. This arranged geometry is then optimized to find the derivative local minimum using the Berny equation. Which corresponds to the transition state. From this the geometries and energy of the transition state can be found.

Synchronous transit- guided quasi-newton method, this method does not require an approximation of the transition state geometry but instead the reagent and product structures^[7]. the QST method first interpolates^[8] between the reagent and the product given and then optimizes (using a quasi-newton and eigenvector following algorithm^[9]) towards a saddle point.

There are also two theory levels of different accuracy that each calculation method could be performed to, HF/3-21G using the hartree fock calculation method, the less accurate level, and B3LYP/6-31G which uses DFT .^[10]

These methods were applied to find transitions state geometries of a cope rearrangement of 1,2 hexadiene and two diels alder cycloadditions.

Nf710 (talk) 15:04, 3 December 2015 (UTC)This is an excellent introduction, you have covered all the methods used in the experiment and to a decent level of detail. Good explanation of the QST method!

The Cope Rearrangement Tutorial

Background

The Cope Rearrangement is a [3,3] sigma-tropic pericyclic rearrangement of a 1,5-diene. In this experiment, the Cope Rearrangement of 1,5-hexadiene is analysed using Gaussian calculations. In pericyclic reactions, Woodward-Hoffmann rules are used to show if a reaction is thermally allowed;depending on the total number of (4q+2)_s + (4r)_a components, if the total number is odd (where q and r are whole numbers, s=suprafacial and a=antarafacial) then the reaction is thermally allowed. This cope rearrangement of 1,5-hexadiene has two _π2_a components and one _σ2_s component and therefore this reaction is allowed thermally. As only suprafacial components are included the reaction must proceed through disrotation.

Nf710 (talk) 15:04, 3 December 2015 (UTC) Good knowledge of the chemistry

Conformers of 1,5-hexadiene

Conformer	Point Group	Energy/Hartrees HF/3-21G	log files
gauche2	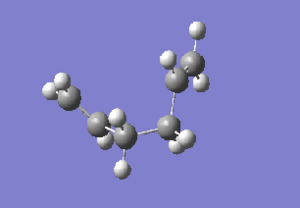C₂	-231.69166	here
anti2	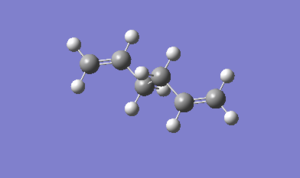C_i	-231.69253	here
gauche3	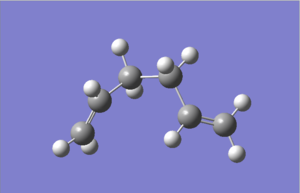C₁	-231.69266	here
anti1	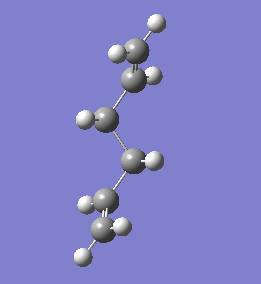C2	-231.69260	here

It was expected for anti2 conformer of 1,5-hexadiene to be the most favored with the lowest energy but the calculations show the gauche2 is a more stable conformer. This is due to secondary orbital overlap between the two pi systems reducing the total molecular energy.

Nf710 (talk) 15:09, 3 December 2015 (UTC) Nice explanation, you could have proved it by looking at the orbitals from the .chk file

Anti2 1,5-hexadiene Re-optimisation

Compound Anti2 was then optimized using B3LYP/6-31G*, producing a medium level of accuracy. There is a large difference in energy from the HF/3-21G optimized structure, 2.867 a.u, but this value is irrelevant due to the varying zero level energy. The over all geometry is visibly similar but there are subtle changes.

Bond	HF/3-21G Bond Length (Å)	B3LYP/6-31G* Bond Length (Å)
1-2	1.31613	1.33824
2-3	1.50891	1.50720
3-4	1.55275	1.55504
4-5	1.50891	1.50720
5-6	1.31613	1.33824

The largest difference is of the C1-C2 and C5-C6 bond lengths, implying that B3LYP/6-31G* is more accurate than HF/3-21G when it comes to molecules containing double bonds, B3LYP/6-31G* method can better calculate the effect that pi bonds have on a molecules geometry ^[11]. The B3LYP/6-31G* values for C1-C2 and C5-C6 bond lengths mach closer to literature values (approx~ 1.33 Å)

Atoms in Dihedral Angle	HF/3-21G Bond Angle	B3LYP/6-31G* Bond Angle
1-2-3-4	-114.66877	-118.79130
3-4-5-6	114.66877	118.79130

The system is sp²therefore an angle of 120 is expected, the B3LYP/6-31G* method is yet again more accurate when comparing dihedral angles to expected values.

Nf710 (talk) 15:11, 3 December 2015 (UTC) very nice and clear comparison of the geoms

Frequency Results of Anti2 1,5-hexadiene

These are all as expected. The frequency results are related to the second derivative of the potential energy surface. Therefore determining if a stationary point is a maximum (k=negative where k is the force constant) or a minimum (k=positive) can be done from the frequency results. All the frequency results are real which indicates a minima. This confirms that a low energy reactant was produced from the optimization. The log file can be found here.

Nf710 (talk) 15:14, 3 December 2015 (UTC) good understanding of frequency calculation but you forgot the thermochemistry.

Chair and Boat Transition Structures

Two different input methods are used here. One for the chair structure and one for the boat structure.

Chair structure

The method used here was to optimize the reagents individually and then arrange them in a manner that is similar to the expected transition state. This is loosely using the Hammond-Leffler Postulate. The arranged reagent molecules are then optimized using the Berny algorithm which will optimize the structure to a maximum, ie to the transition state. When frequency calculations are made there is a single imaginary frequency due to the optimized structure being a transition state. Transitions states reside on maxima of the potential energy surface producing a negative K which when square rooted will produce an imaginary result.

Optimization of reagents, two acyl fragments, using HF/3-21G. Log file here

Arrangement of optimized acyl fragments. The acyl fragments were arranged staggered, with a 2.2 Å inter-nuclear distance between each terminal carbon, and a point group symmetry of C_2h. This proposed transition state was then optimized using the Berny algorithm and selecting to calculate force constants once which produces the transition state shown below, with an imaginary frequency at -818.12 cm^-1. Log file here

Chair transition state vibration

Arrangement of optimized acyl fragments using frozen coordinate method. As before the fragments are arranged 2.2 Å apart, but this time the distance is fixed using the redundant coordinate editor on GaussView, ensuring the terminal carbons will be 2.2 Å apart in the optimized product. The Berny algorithm is then used to produce the chair transition state calculated from this input, which is very similar to the previously produced, unfrozen, chair transition state. Log file here

Redundant coordinate editor

Chair transition state vibration

Method	Optimized Terminal Carbon Inter-nuclear distance	Imaginary Frequency cm^-1	Energy/Hartrees HF/3-21G
Non-Frozen	2.01975Å	-818.12	-231.61932
Frozen	2.2 Å	-817.89	-231.61518

Nf710 (talk) 15:34, 3 December 2015 (UTC) All your energies are correct

Boat Structure

The boat transition state was found using and alternative method. instead of optimizing ta proposed transiting state, two separate structures were optimized, one being the reagent and one being the product. Then using the QST2 method (Quasi-Newton Synchronous Transit-guided method described in the introduction). The transition state is found from these two structures. For the QST2 method to work the reagent and the product must be labeled correctly as shown below. For this transition state the Anti2 1,5-hexadiene previously optimized was used.

This produced and unfavorable distorted transition structure resembling the chair transition state.

The failure of this optimization can be counteracted by altering the geometry of the reagent and product structures. By rotating the middle C-C bond, reducing the dihedral angle to 0°, the calculation is better directed to the boat transition state.

this was succesful! here An imaginary frequency was found at -839.86cm^-1 proving that a transition state was found.

Boat transition state vibration

Intrinsic Reaction Coordinate

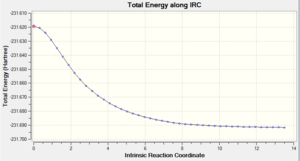
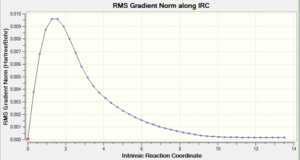
this is a pathway/slice of the potential energy surface giving a 1D surface running along the path of lowest energy, from one minima to another ^[12] The IRC is used here to plot the forward progression (symmetrical reaction therefore only one direction needs to be calculated) of the reaction from he boat transition state found. the accuracy can be increased by increasing the number of recorded points along the pathway, 50 points was found to be sufficient for the accuracy needed to find the minium.

The total energy vs IRC graph shows the pathway from the transition state to the product residing at a minimum energy stationary point. This is supported by the graph of the derivative, RMS Gradient Norm vs IRC, which goes to zero when the potential energy surface is at a minimum.

Nf710 (talk) 15:41, 3 December 2015 (UTC) Nice IRC but you didnt work out which conf it connects.

Comparison of Re-optimized Transition states

Both of the transition state structures where re-optimized using the B3LYP/6-31G* level of accuracy.

Transition State Conformer	Energy (Hartrees) (cms^-1)	Bond forming lengths (Å)	log file
Chair HF/3-21G	-231.6193	2.0195	here
Chair B3LY/6-31G	-234.5569	1.96614	here
Boat HF/3-21G	-231.6028	2.14005	here
Boat B3LY/6-31G	-234.5430	2.20663	here

The activation energy was calculated for the two transition states, from the difference in the the sum of electronic and zero-point energies for the transition state and the Anti2 1,5-hexadiene reactant. This value was then converted to kcal/mol (1 hartree= 627.509 kcal/mol ).

Transition State Conformer	Sum of electronic 'and zero-point' energies at 0 K	Sum of electronic 'and thermal' energies at 0 K	Electronic energy	ΔE Activation Energy at 0 K kcal/mol
Chair HF/3-21G	-231.4638	-231.4581	-231.5627	47.53
Chair B3LY/6-31G	-234.41491	-234.40899	-234.54698	34.08
Boat HF/3-21G	-231.4509	-231.4452	-231.5688	55.62
Boat B3LY/6-31G	-234.4034	-234.3782	-234.4437	41.28

From the activation energies we can see that the chair transition state will be formed first as it is the lower energy transition state. A lower energy transition state leads to the kinetic product so we can determine from this that the chair product is the result of kinetic favour.

When comparing the basis sets the general visual outcome is very similar and most of the geometries between the HF/3-21G and the B3LY/6-31G methods are close but the energies tend to vary more. The B3LY/6-31G basis set is more accurate over all.

Nf710 (talk) 15:56, 3 December 2015 (UTC) great comparison of the geoms. unfortunately your energies are slightly wrong, perhaos you were using the wrong basis set. you also didnt compare with experiment or do a freq calc on B3LYP

Nf710 (talk) 15:56, 3 December 2015 (UTC) In general this part of the report was good. i was particularly impressed by your introduction as you showed extensive understanding of the methods and it was well referenced

Diels-Alder Cycloadditions

Background

The Diels-Alder reaction is a [4+2]-cycloaddition between a dienophile and a diene. Due to π-orbital overlap two σ-bonds are formed in place of the π-bonds, sigma bonds are much stronger causing the overall reaction to be thermodynamically favourable. Below are details of the reactions of ethylene with cis-butadiene; and cyclohexa-1,3-diene and maleic anhydride.

Butadiene and Ethene Diels Alder Reaction

The reagents, Butadiene and Ethene were optimised using the AM1 method. AM1 is very efficient due to making assumptions.^[13] AM1 is a a good basis for a calculation.

(This is perhaps a little brief for an introduction about why you are using AM1. Also, your log files (thank you for adding them) show you've been using a mixture of PM6 and HF Tam10 (talk) 16:19, 1 December 2015 (UTC))

Butadiene LUMO	Butadiene HOMO	Ethene LUMO	Ethene HOMO

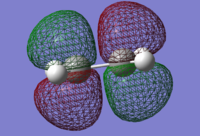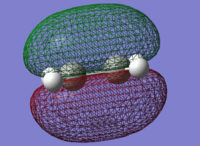
here		here

(What's the symmetry of these MOs and the HOMO and LUMO of the TS? This is important as the TS MOs are formed from a combination of orbitals from ethene and butadiene that are of the same symmetry Tam10 (talk) 16:19, 1 December 2015 (UTC))

The reagents were then arranged in a manner similar to the expected transition structure. If the guess structure for the transition state is far for the idea structure then the Berny algorithm may not work as the curvature of the surface may alter the direction of the calculation if the starting structure far from ideal.

	Transition State HF/631G*	Literature Values^[14]
Imaginary Frequency	-902.63	--
Energy/Hartrees HF/3-21G	-232.87960559	-232.79942
Terminal Carbon Inter-nuclear distance	2.0205 and 2.20204	2.079
log	here

(This comparison you have with literature is actually very off (1 AU =~2625 kJ/mol so 0.08 AU =~210 kJ/mol). As it turns out, you've compared to a calculation that takes the geometry from the HF/6-31 calculation and performs a single point energy calculation with HF/6-31G(d). You have the correct value (for HF/6-31G(d)) if you look just one row down in the paper. However, your table writes HF/3-21G. I assume you forgot to change the basis set Tam10 (talk) 16:19, 1 December 2015 (UTC))

Comparison with literature shows that the optimization was successful and the same transition state has been found.

(Why are you reporting two inter-nuclear distances? Did you have an asymmetric TS? What can you say about this length (compare to typical sp3(C), sp2(C) and WdV(C))? Tam10 (talk) 16:19, 1 December 2015 (UTC))

Cyclohexa-1,3-diene and maleic anhydride Diels Alder Reaction

The reagents, Cyclohexa-1,3-diene and maleic anhydride were optimised using the AM1 method.

(These are all HF or B3LYP calculations, not AM1 Tam10 (talk) 16:19, 1 December 2015 (UTC))

Cyclohexa-1,3-diene LUMO	Cyclohexa-1,3-diene HOMO	maleic anhydride LUMO	maleic anhydride HOMO

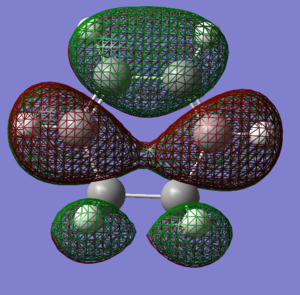
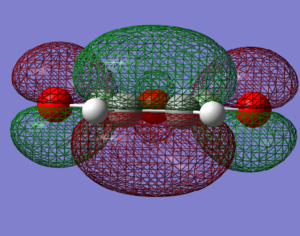
here		here

The reagents were then arranged in a manner similar to the expected transition structure and optimized using AM1 to a minimum. This arrangement will be used as the starting structure for the QST2 calculation. The exothermic product was then optimized using AM1 and then HF/3-21G.

-

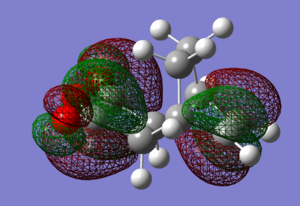
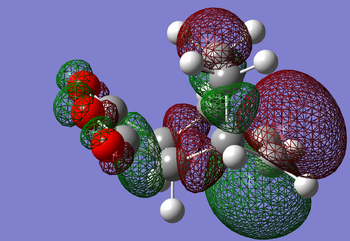
For the QST2 method to work the reagent and the product must be labeled correctly as shown above.

-

For the Berny method the guess transition structure was arranged with a distance of 2.05332 2.00000

the Berny method transition state vibration

Exothermic Product	Transition State TS Berny Method	Transition State QST2 Method
Imaginary Frequency	-647.54	-647.38
Energy/Hartrees HF/3-21G	-605.6036	-612.66717746
Bonding Carbons Inter-nuclear distance	2.26045 2.26090	2.25998 2.26140
Image
Log	here	here

Comparison of Exothermic and Endothermic Product

(In this context, endo and exo are not the same as endothermic and exothermic! Tam10 (talk) 16:19, 1 December 2015 (UTC))

Here I have used the QST2 method to compare as the Exothermic QST2 results were found to be more accurate.

	Exothermic Product Transition State	Endothermic Product Transition State
Imaginary Frequency	-647.38	-1008.30
Energy/Hartrees HF/3-21G	-612.66717746	-605.53879
Bonding Carbons Inter-nuclear distance	2.25998 2.26140	1.51770 1.65285
Image
Log	here	here

(This is the wrong endo TS. Below I've added a Jmol to show what you have as it's not obvious to see from the image you've provided Tam10 (talk) 16:19, 1 December 2015 (UTC))

When comparing the energy of the two structures, this can be done as both were optimized by the say method and level of accuracy, it can be seen that the endo transition state is of a lower energy there for the endo product is also the kinetic product of this reaction. The endo transition state is of a lower energy due to the secondary orbital overlap effect.

(This is not true - they are different methods. If you calculate the energy difference between them it would come to nearly 19 MJ/mol! This is an indication that you're using different methods and/or basis sets Tam10 (talk) 16:19, 1 December 2015 (UTC))

Conclusion

Gaussian was successfully used to study an aspect of reactions which is not experimentally available. The ability to calculate energies and vibrations of a transition state of a reaction allows us to research the reaction mechanism to a deeper level. Gaussian was used in this experiment to research the orbital over lap which causes certain transition state geometries to be favorable within the Cope and Diels-Alder reactions. by using the surface tool it was seen that secondary orbital effects cause certain transition state geometries to occur. When it came to the calculations Hartree-Fock 3-21G and Density Functional Theory 6-31G produced similar results except Density Functional Theory 6-31G is more accurate when it comes to the energies. AM1 produced slightly different results due to the simplified semiempirical methods which do not take into account the secondary orbital overlap. Throughout this experiment my knowledge on the gaussian and gaussView software and of force constants and certain algorithms has been drastically developed.

↑ http://vergil.chemistry.gatech.edu/courses/chem6485/pdf/Hartree-Fock-Intro.pdf
↑ http://web.ornl.gov/~pk7/thesis/pkthnode13.html
↑ http://newton.ex.ac.uk/research/qsystems/people/coomer/dft_intro.html
↑ http://www.cup.uni-muenchen.de/ch/compchem/energy/semi1.html
↑ http://www.gaussian.com/g_whitepap/qst2.htm
↑ http://www.gutenberg.us/articles/Transition_state
↑ http://www.gaussian.com/g_tech/g_ur/k_opt.htm
↑ http://www.cup.uni-muenchen.de/ch/compchem/geom/stqn.html
↑ http://www.gaussian.com/g_whitepap/qst2.htm
↑ http://www.computationalscience.org/ccce/Lesson2/Notebook%202%20Lecture.pdf
↑ https://books.google.com/books?id=QI3LBQAAQBAJ&lpg=PA113&ots=6c_CutlF2B&dq=B3LYP%2F6-31G*%20pi%20bonds&pg=PA116#v=onepage&q=B3LYP/6-31G*%20pi%20bonds&f=false
↑ file://icnas1.cc.ic.ac.uk/jd2613/yr%203/autumn%20term/comp/9789048138609-c2.pdf
↑ http://www.gaussian.com/g_tech/g_ur/k_semiempirical.htm
↑ http://www.chem.wayne.edu/schlegel/Pub_folder/108.pdf

[1] ttp://vergil.chemistry.gatech.edu/courses/chem6485/pdf/Hartree-Fock-Intro.pdf

[2] ttp://web.ornl.gov/~pk7/thesis/pkthnode13.html

[3] ttp://newton.ex.ac.uk/research/qsystems/people/coomer/dft_intro.html

[4] ttp://www.cup.uni-muenchen.de/ch/compchem/energy/semi1.html

[5] ttp://www.gaussian.com/g_whitepap/qst2.htm

[6] ttp://www.gutenberg.us/articles/Transition_state

[7] ttp://www.gaussian.com/g_tech/g_ur/k_opt.htm

[8] ttp://www.cup.uni-muenchen.de/ch/compchem/geom/stqn.html

[9] ttp://www.gaussian.com/g_whitepap/qst2.htm

[10] ttp://www.computationalscience.org/ccce/Lesson2/Notebook%202%20Lecture.pdf

[11] ttps://books.google.com/books?id=QI3LBQAAQBAJ&lpg=PA113&ots=6c_CutlF2B&dq=B3LYP%2F6-31G*%20pi%20bonds&pg=PA116#v=onepage&q=B3LYP/6-31G*%20pi%20bonds&f=false

[12] ://icnas1.cc.ic.ac.uk/jd2613/yr%203/autumn%20term/comp/9789048138609-c2.pdf

[:0-13] ttp://www.gaussian.com/g_tech/g_ur/k_semiempirical.htm

[14] ttp://www.chem.wayne.edu/schlegel/Pub_folder/108.pdf

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]