Rep:Mod:jc6412TS

Introduction

The use of Gaussian software in this computational exercise enabled the calculation and identification of transition states (TS) for two different reactions, namely the Cope Rearrangement and Diels Alder cycloaddition reactions. For the Cope Rearrangement, both reactants and products were optimized at Hartree-Fock (HF) and Density Functional Theory (DFT) levels of theory. Estimations and illustrations of various geometries of the conformers resulting from the Cope rearrangement were firstly computed, and subsequently optimized to a minimum on the potential energy surface (PES). The optimized structures were compared to a reference table provided (Appendix 1).

Additionally, the "Chair" and "Boat" transition structures were also investigated in this exercise. The initial guess TS was optimized to check if it corresponded to a saddle point. This was done by undertaking frequency calculations and identifying an imaginary frequency, which corresponded to a saddle point of the potential energy surface. There are three methods used to optimize a transition structure – computing force constants at beginning of calculation, using the redundant coordinate editor, Quadratic Synchronous Transit (QST2) and also QST3. All these methods used would be discussed further in the following sections. Finally, calculated activation energies obtained at HF and DFT levels of theory were compared to pre-calculated and experimental values.

The Diels Alder Cycloaddition reaction involved locating transition structures on PES of two systems; one is a prototypical reaction involving ethylene and 1,3-cis butadiene, and the other involving maleic anhydride with cyclohexa-1,3-diene. The molecular orbitals (MOs) were analysed and used to investigate the interaction between the orbitals of reacting molecules. The activation energies were also tabulated and compared to literature values to determine the accuracy of calculation at different levels of theory.

The electronic structure modelling program used for the exercise was GaussView 5.0.9 (GaussView does not actually do the any electronic structure calculations. It just sets the inputs -and reads the outputs- of Gaussian that runs the calculation in the background. João (talk) 16:51, 10 March 2015 (UTC)). This particular software makes use of Gaussian type orbitals (GTO) instead of Slater type orbitals (STO). Gaussian type orbitals are functions acting as atomic orbitals in the Linear Combination of Atomic Orbitals (LCAO) method used to represent electron orbitals in a molecule. Many properties depend on this calculations. The Slater basis function is very useful due to it exhibiting cusps at the nuclei and ability to decay exponentially (It is not so much that Slater orbitals are "useful". They correspond to a better description of the electronic density in atoms. For a discussion of STO vs GTO see for example doi:10.1021/ed500437a. João (talk) 16:51, 10 March 2015 (UTC)). However, the Gauss basis function is still preferred as the Slater basis set is very time-consuming to compute and is often restricted to evaluate small molecules ¹. The Gaussian Product Theorem is the prime reason for use of GTO. This theorem guarantees a finite sum of Gaussians in the centre of a point along the axis connecting the centre of two GTOs of two different atoms being obtained from their product. Although the use of GTOs results in simpler integrals compared to those of STO, more orbitals/functions are required for Gaussian than Slater in order to achieve a similar basis set. Thus, a longer time would be required for calculation, deeming it as a more costly method ¹. Nonetheless, the increase in speed and yield of electron orbital integrals greatly outweighs the costs incurred from the need of more orbitals in the Gaussian calculation ².

Cope Rearrangement Tutorial

The [3,3]-sigmatropic shift rearrangement is a pericyclic reaction where a sigma bond is switched with another in an intramolecular fashion. The Cope Rearrangement occurs via this particular reaction which has been widely investigated for better understanding of the mechanism involved. Based on the Woodward–Hoffman rules, it can be predicted that these six electron reactions would proceed in a suprafacial shift, via a Huckel transition state (TS) ³.

Despite it being widely studied, the mechanism is still controversial up till today. It has been proposed to undergo via either a concerted, stepwise or dissociative method. There has been various propositions that the mechanism might include consecutive steps via a diradical intermediate. Nonetheless, it is however generally accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy ⁴. This is due to the chair conformer experiencing less steric hindrance between hydrogen atoms. Therefore, it is evident that the "chair" conformer is preferred over the "boat" conformer due to greater stability possessed by the former compared to the latter.

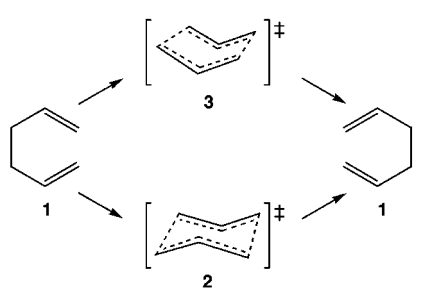
Both the "chair" and "boat" structures can be shown in Figure 1 ⁵ as conformers 2 and 3, respectively as shown below.

Figure 1. Boat and Chair TS during Cope rearrangment

Optimizing the Reactants and Products

Part a

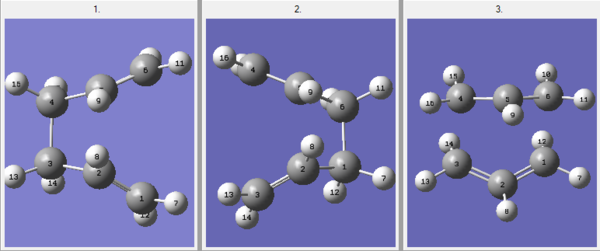
A molecule of 1,5-hexadiene with an "anti" linkage for the central four C atoms was drawn, cleaned and then optimized at the HF/3-21G level of theory. The four different conformers of 1,5 Hexadiene with "anti" linkages are represented in Table 1. The tabulated energies and point groups of the various conformers are also indicated in the table below.

Table 1. Different conformers of 1,5 Hexadiene adopting the "anti" linkage.

Anti 1

Anti 2

Energy (Hartrees)

-231.69260235

-231.69253516

Point group

C₂

C_i

Anti 3

Anti 4

Energy (Hartrees)

-231.68907066

-231.69097055

Point group

C_2h

C₁

From the result summary, the energy of the first conformer drawn was tabulated to be -231.69260 (Hartree units). This resembles that of an Anti 1 structure as represented in Table 1 above. Moreover, with the use of the Symmetrize function, the final structure appeared to have a symmetry with a point group of C₂.

Part b

A molecule of 1,5-Hexadiene with a "gauche" linkage for the central four C atoms was drawn. It was expected that the gauche structure would possess a higher energy than the optimized anti structure due to the steric hindrance experienced by the terminal hydrogen atoms towards the rest of the molecule. The six different possible conformers with "gauche" linkages were constructed and are represented in Table 2. The tabulated energies and point groups for the various molecules are also shown in the table below.

Table 2. Different conformers of 1,5-Hexadiene adopting the "gauche" linkage.

Gauche 1

Gauche 2

Gauche 3

Energy (Hartrees)

-231.68771617

-231.69166702

-231.69266121

Point group

C₂

C₁

Gauche 4

Gauche 5

Gauche 6

Energy (Hartrees)

-231.69153034

-231.68961575

-231.68916017

Point group

C₂

C₁

After optimization of the structure at the HF/3-21G level of theory, the final energy recorded for gauche 1,5-Hexadiene was -231.69166702, which corresponded to Gauche 2 (Why do you highlight this value? João (talk) 16:51, 10 March 2015 (UTC)). This value recorded is greater than that of the Anti 2 structure which is expected of a gauche structure due to greater steric hindrance experienced by the latter. The final structure have a symmetry with a point group of C₂.

Part c

Upon comparing the geometries of both Anti 2 and Gauche 6 conformers shown above, there is an obvious structural difference which may cause this energy difference. It can be observed from Tables 1 and 2 that there is clearly a correlation between the energy levels of the molecule and the number of s-cis C_sp² - C_sp³ bonds. This correlation is summarized into Table 3, below. It is evident that the molecule with the highest number of this specific s-cis bonds tend to possess higher energy levels than those with fewer/ without these bonds. A reasonable explanation for this is because the presence of the C_sp² - C_sp³ leads to greater repulsive steric hindrance experienced between the vinyl terminal protons with the rest of the molecule ⁶. It can be deduced from theoretical knowledge that greater steric hindrance would lead to a molecule to possess higher energy resulting in lowered stability. The table below represents the number of energies, conformers and the trend associated with the number of s-cis bonds: (Interesting analysis. João (talk) 16:51, 10 March 2015 (UTC))

Table 3. Correlation table between presence of s-cis bonds with energy levels arranged in ascending order of energy
Conformer	Number of s-cis linkages	Energy (Hartrees)
Gauche 3	0	-231.69266121
Anti 1	0	-231.69260235
Anti 2	0	-231.69253516
Gauche 2	0	-231.69166702
Gauche 4	0	-231.69153034
Anti 4	1	-231.69097055
Gauche 5	1	-231.68961575
Gauche 6	1	-231.68916017
Anti 3	2	-231.68907067
Gauche 1	2	-231.68771617

Nonetheless, it is important to note that unlike what was discussed previously, the gauche conformer is the one with the lowest energy conformation. This contradicted with what was discussed in Section (b) about the gauche molecule possessing higher energy as a result of greater steric hindrance. This occurrence could be attributed to that of favorable C-H/π interactions present in the conformer Gauche 3, making it more stable than the other 9 conformers, including those with "anti" linkages which were expected to be more stable ⁷. This finding was presented by Gung et al, using the DFT (BY3LYP/6-31G*) model.

Both DFT and HF methods take into account the kinetic energy of electrons, electron-nuclei interaction, coulomb interactions and exchange correlation⁸. The difference between the DFT and HF method is that the former takes into account larger basis sets and also electron correlation ⁹ but only the exchange correlation is accounted for by the latter. Thus, it is impossible to simply predict the lowest energy conformer by simply using the HF (Why do you say it is impossible to predict? One can make a prediction knowing that approximations are involved. João (talk) 16:51, 10 March 2015 (UTC)) as there are other factors such as attractive interactions (What kind of attractive interactions do these calculations neglect? João (talk) 16:51, 10 March 2015 (UTC)) and electron correlation that need to be taken into account in order to make substantive comparisons between various conformers.

Part d and e

With reference to that of Part (a), (b) and (c), it can be concluded that the structures optimized are those illustrated in both tables. Similarly, the Anti 2 structure has also been located as represented in Table 1 specifically.

Part f

The C_i Anti 2 conformer of 1,5-Hexadiene was then reoptimized at the B3LYP/6-31G* level (DFT). The energy tabulated amounted to -234.55970, as opposed to -231.69254 obtained from using HF/3-21G. As mentioned previously, the former method takes into account electron correlation as opposed to the latter method that does not. In other words, the DFT method takes into account larger basis set (Note that including electron correlation -improving the method to calculate the electronic energy- and augmenting the size of the basis set are two distinct things. Both improve the "quality" of the calculation. João (talk) 16:51, 10 March 2015 (UTC)), deeming it a more effective method for more accurate calculations ⁹. The overall geometry of both molecules differed in terms of bond length and dihedral angles, which are represented in Table 4, below.


Figure 2. Anti 2 conformer with numbered carbon atoms

Table 4. Differences in geometry of Anti 2 using HF/3-21G and B3LYP/6-316*

	Bond lengths (Å)			Dihedral angle (°)
	C1-C2	C2-C3	C3-C4	C1-C2-C3-C4	C2-C3-C4-C5	C3-C4-C5-C6
HF/3-21G	1.31618	1.50888	1.55301	-114.63319	180.00000	114.63319
B3LYP/6-31G*	1.33344	1.50418	1.54863	-118.58066	180.00000	118.58066

It could also be observed from Table 4 that the bond lengths for both methods did not deviate too much. However, it may be good to note that the bond length of the double bond (C1-C2) calculated at the DFT level of theory was higher by 0.02206 Å compared to HF whereas the bond length of C2-C3 is slightly shorter for the former. For the DFT optimized Anti 2 conformer, the 'terminal' dihedral angles (between C1-C2-C3-C4 and C3-C4-C5-C6) was measured to be 118.79158°, around 4° larger than that optimized by HF. The dihedral angle of the centre four atoms optimized by DFT and HF remained the same, at 180°. These results are expected as taking into account electron repulsion of the electronic structure would mean greater bond length and larger dihedral angle. Thus, unlike the HF method that takes into account only the exchange correlation (potential energy due to spin and charge), the DFT method takes into account both electron and exchange correlation, revealing even more accurate dihedral angles and bond lengths ⁸.

Part g

The final energies given in the output file represent the energy of the molecule on the bare potential energy surface. To be able to compare these energies with experimentally measured quantities, some additional terms need to be included and they often require a frequency calculation. The frequency calculation is calculated by firstly calculating the second derivatives to give force constant which is used to solve the frequency ¹⁰. The frequency calculation can also be used to characterize the critical point - data obtained with all real vibrational frequencies confirms the identity of a structure being at a minimum.

The sum of electronic and zero-point energies, the sum of electronic and thermal energies, the sum of electronic and thermal enthalpies, and the sum of electronic and thermal free energies were tabulated and recorded as represented in Table 5, below. The first of these is the potential energy at 0 K including the zero-point vibrational energy (E = E_elec + ZPE), the second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + E_vib + E_rot + E_trans), the third contains an additional correction for RT (H = E + RT) which is essential when understanding dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS) ¹¹.

Table 5. Summary of energies of optimized Anti 2 conformer calculated at B3LYP/6-31G* level of theory at 298.15 K and 0 K
Structure	Temperature / K	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies
	298.15	-234.611710	-234.469218	-234.461866	-234.460922	-234.500814
	0	-234.469218	-234.469218	-234.469218	-234.469218	-234.469218

Based on the results above, it can be observed that the various energies at 298.15 K are different due to the different as different energies are taken into account, however at 0 K, the only contributions come from the sum of electronic energies and zero point energies. Thus, there are no changes observed for all the other energies, with no contribution from thermal enthalpies and free energies respectively.

The infrared spectrum from the frequency analysis is shown in Figure 3, below.


Figure 3. Labelled IR spectrum

The expected peaks are all identified in from the IR spectrum obtained and they corroborate with literature values ¹².

Optimizing the "Chair" and "Boat" Transition Structures

The chair and boat conformers are two possible transition states in the Cope rearrangement of 1,5-Hexadiene. This section focuses on setting up of transition structure optimization via three different methods as mentioned previously. Theses methods include computing of the force constants at the beginning of the calculation, using the redundant coordinate editor and also using QST2.

It is good to note that transition state optimizations are more difficult than minimizations because the calculation needs to know the position negative direction of curvature. The suitability of the method utilized is highly dependent on the type of guess molecule present. Computing the force constant matrix (Hessian) in the first step of the optimization which will then be updated as the optimization proceeds would be the easiest way if a reasonable guess structure has been constructed. However, for a guess transition structure that deviates too much from the exact structure, the approach may not work as the curvature of the surface may be significantly different, resulting in calculation errors. In some cases, a better transition structure can be generated by freezing the reaction coordinate (using Opt=ModRedundant)and minimizing the rest of the molecule. Once the molecule is fully relaxed, the reaction coordinate can then be unfrozen and the transition state optimization starts again. An advantage of doing this, is that it may not be necessary to compute the whole Hessian once this has been done, and just differentiating along the reaction coordinate might give a good enough guess for the initial force constant matrix. Moreover, this can save a considerable amount of time in cases where the force constant calculation is costly ¹¹.

This exercise also involved the visualization of reaction coordination and running of the Intrinsic Reaction Coordinate (IRC). The activation energies for the Cope Rearrangement via the "Chair" and "Boat" transition structures would also be calculated and discussed below.

Part a

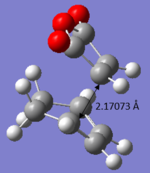
The allyl fragment CH₂CHCH₂ was drawn and optimized using the HF/3-21G level of theory. This is represented as Figure 4, below. This fragment possesses a C_2v point group. The optimized allyl structure from the first calculation was pasted twice into the new window. The two allyl fragments were then adjusted to look similar to the chair transition state as given in Appendix 2. This is the guess chair transition state structure which is represented in Figure 5.


Figure 4. Gaussview image of an optimised allyl fragment.		Figure 5. Gaussview image of an guess chair transition state.

Following this section of the exercise, the first method (Hessian) was used to optimize the guess chair transition structure since a guess structure of the chair transition state has been constructed. The results can be shown in Part b, below.

Part b

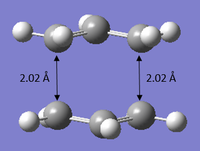
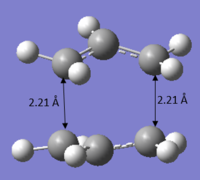
A Gaussian optimization for a transition state was set up. The molecule was optimized to TS (Berny) and the frequency was calculated at HF/3-21G level of theory. The distance between the terminal ends of of the allyl fragments were set to about 2.2 Å apart. After optimization, it can be observed that the distances between the terminal ends of both fragments were set at about 2.02 Å apart and the C-C-C angle of each individual fragment is given as 120.503^°. The molecule has a point group of C_2h It can also be extracted from the results that an imaginary frequency of magnitude 817.86 cm^-1 was identified after the calculation, confirming the identity of the transition state. The vibration of the chair transition state is illustrated in the animation shown below, which is expected for that of the Cope rearrangement.


Animation of vibration in chair transition structure

Part c and d

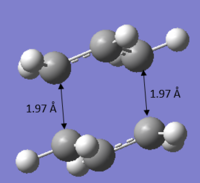
The transition structure was then optimized again using the frozen coordinate method. Both bond and Freeze Coordinate were options selected under the "Redundant Coordinate Editor". The distance between the 4 terminal atoms (where bond breaking/forming occurs) was frozen, allowing the unfrozen parts to be optimized to a minimum under the HF/3-21G basis set and later unfrozen and re-optimized to generate the transition strcture. The optimized "Chair" structure can be represented in Figure 6 below.


Figure 6. Optimized "chair" structure using Frozen Coordinate method

It can be observed that the optimized structure obtained above looks a lot like the transition structure optimized in part (b) calculated using the computational of force constant matrix. The only difference is that the bond forming and bond breaking distances were fixed at 2.20 Å. These distances were then optimized. A normal guess Hessian modified was used to include the information about the two coordinates that are differentiating along.

The bond forming/bond breaking bond lengths, electronic energies and imaginary frequencies of the transition structure were compared between the two different methods used and can be summarized in the Table 6 below.

Table 6. Bond breaking/forming distance using force constant matrix and frozen coordinate method

	Chair TS optimization Method
Type of bond	Computation of force constant matrix	Frozen coordinate method
Bond forming/breaking distance Å	2.02088/2.02085	2.02073/2.02070
Imaginary Frequency/ cm^-1	817.86	817.86
Electronic Energy (Hartree)	-231.61932237	-231.61932233

Based on results above, it is evident that both methods resulted in very similar transition state structures. This is not surprising since the primary focus is to locate the TS using different methods. The electronic energy (-231.619322 Hartree) and imaginary frequency (817.86 ^-1 were observed to be fundamentally similar for the two methods since the same level of theory (HF/3-21G) was utilized for the calculations. Using the same level of theory meant that the various interactions accounted for would be the same for both methods used. Therefore, no deviations would be observed for both the structure, energy and vibrations. However, if a higher level of theory, such as BYLP3/6-31G* was used, the results might differ slightly with reasons explained in the previous sections. These reasons include DFT using larger basis sets and taking into account of electron correlation, resulting in more accurate calculations ⁹.

The only slight difference between using the force constant matrix method and Frozen Coordinate method lies in the former being effective for when the guess structure with very close resemblance to the actual transition state. The latter method, however, is a better method since the molecule (other than the the frozen coordinates) would be optimized before the transition state is found and the distances were further re-optimized again. Thus, the Frozen method is more effective for a guess molecule TS structure that does not closely resemble the actual TS. (This is true, but do you always know which coordinates to freeze? João (talk) 16:51, 10 March 2015 (UTC))

Part e

The boat transition structure was optimized using the QST2 method. In this method, the specification of reactants and products for a reaction would allow interpolation between the two structures to be done by the calculation so as to try to find the transition state between them. The reactants and products were manually numbered to the structures as shown below in Figure 7, with 1 showing the reactant and 2 the product.


Figure 7. Initial optimized reactants and products

The first QST2 calculation was carried out but failed. The calculation failed due to the structure looking a bit like the chair transition structure but more dissociated, as shown below. When the calculation was linearly interpolated between the two structures, no consideration was given to the top allyl fragment that could be easily translated. This led to the possibility of a rotation around the central bonds, thereby causing a failure in calculation. It is evident that the QST2 method was indeed unsuccessful for locating the boat transition structure if it started from the structures of reactant and product as shown in Figure 7. It can be concluded from Figure 8 that there was incorrect bond breaking and forming of transition structure which revealed that it was necessary to manipulate the structures slightly in order for a more accurate calculation to be carried out.


Figure 8. Incorrect bond breaking and bond forming of transition structure

The geometries of the reactant and product were manipulated to resemble the boat transition structure more. For both the reactant and product molecule, the central C-C-C-C dihedral angle (i.e. C2-C3-C4-C5 for the molecule above) and change the angle to 0^o. The inside C-C-C (i.e. C2-C3-C4 and C3-C4-C5 for the molecule above) was then selected and reduced to 100^o. This alteration led to both reactant and product molecules should now look like 1 and 2 respectively as shown in Figure 9 below.


Figure 9. Optimized reactants and products after re-orientation

After the alteration, the calculation was indeed successful and led to the summaries of values as represented in Table 7 below.

Table 7: Optimization Summary for Boat Transition Structure using the QST2 method
Data	Value
Optimized structure
Energy of TS	-231.60280197
RMS Gradient Norm	0.00007476
Point group	C_2v
Value of Imaginary Frequency /cm^-1	-840.0170

Based on this exercise using QST2, it can be concluded that it is indeed a successful method. Nonetheless, it would only be effective if the initial reactant and product structures constructed are close enough to the transition structure. to yield good calculations. Bearing that in mind, it is safe to say that QST2 optimization would only be useful for simple reactions but most likely fail for very complex reactions since it would be difficult to orientate the reactants and products close to the TS. This is because the latter would not allow for interpolation of the calculation to generate a probable transition structure.

An alternative method, QST3 was also used to locate the boat transition structure. This was achieved by generating a guess boat structure and adding it to Molecule Group, resulting in a window with 3 different molecules. The molecules are arranged in the order of reactant, product and the guess boat structure. This is represented in Figure 10, below. (It would have been more interesting to use the QST3 method with the initial structures instead of the modified ones. In the present case, what is the advantage of QST3 with respect to the QST2? João (talk) 16:51, 10 March 2015 (UTC))


Figure 10. Numbered reactant, product and guess boat TS

The QST3 calculation was successfully completed which meant that the original reactant and product effectively converged to generate the boat transition structure. The data values obtained from the successful QST3 calculation are summarized in Table 8 below.

Table 8: Optimization Summary for Boat Transition Structure using the QST3 method
Data	Value
Optimized structure
Energy of TS	-231.60280197
RMS Gradient Norm	0.00007463
Point group	C_2v
Value of Imaginary Frequency /cm^-1	-840.0172

Comparing Tables 7 and 8, it can be concluded that values obtained using both methods are similar, which means that the same transition structure was achieved using both methods. This shows that both methods are equally effective for use in this particular example of Cope rearrangement of 1,5-Hexadiene.

Part f

By looking at the optimized chair and boat transition structures, it is almost impossible to predict which conformer the reaction paths from the transitions structures will lead to. However, there is a method implemented in Gaussian which enables the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This is known as the Intrinsic Reaction Coordinate (IRC) method that creates a series of points by taking small geometry steps in the direction where the gradient of the energy surface is steepest.

As the reaction coordinate is symmetrical, it is only necessary to compute it in the forward direction (out of both directions). The number of points was set to 50 but it was observed that only 44 steps were tabulated. This shows that the calculation stops after the minimum structure has been reached. The IRC pathway was observed in Figure 10 below.


Figure 11. IRC pathway recorded

The product minimum found by the IRC simulation had an energy of -231.69157903 and RMS norm of 0.00015226. With reference to the final structure in Gaussian, it can be observed that it closely resembles the Gauche 2 conformer that was previously discussed, with the energy level deviating slightly from that expected of the Gauche 2 conformer (more similar to Gauche 4) (Could this difference be due to a difference in the convergence criteria in the IRC calculation? Did you compare the RMS norm in one case and the other? The convergence value can be changed. João (talk) 16:51, 10 March 2015 (UTC)). This suggests that the minimum was not successfully reached. Therefore, the final (minimum) structure that was found using the IRC was then further optimised using the HF/3-21G method, in order to generate the real minimum structure.

Optimization of the final IRC structure (Method 1) resulted in the Gauche 2 conformer being obtained. This was reaffirmed by comparing the optimized conformer energy, -231.691667 to that in Appendix 1 which indeed corresponds to that of Gauche 2. Moreover, after optimization, it was noted that the point group changed from C₁ to C₂, which further confirms the identity of Gauche 2.

Optimization through increasing the number of steps in the calculation (Method 2) did not improve the result since the the minimum was found in step 44 and thus terminates at this point. Similarly, computing the force constants in every step (Method 3) was also not an effective solution because was already computed at every step in the previous section. The data obtained for the final structure optimized by Method 1 can be represented in Table 9, below. It is good to note that there are no imaginary frequencies were found, confirming that the identity is indeed a minimum and not a transition state.

Table 9: Re-optimization Summary for Gauche 2 conformer
Data	Value
Optimized structure
Energy of TS	-231.69166702
RMS Gradient Norm	0.00000474
Point group	C₂

Part g

The final part of this exercise includes calculating the activation energies of reaction via both transition structures. In order for these values to be tabulated, both the chair and boat transition structures (from the HF/3-21G) were reoptimized at the B3LYP/6-31G* level of theory and frequency calculations were carried out. Once the calculations have converged, both the geometries and the difference in energies between the reactants and transition states at the two levels of theory were compared. The geometries and energies of the chair and boat TS at both levels of thoery are summarized in Table 10. It can be deduced that the geometries of the respective transition structures are reasonably similar (by comparing the bond breaking/forming distances), but the energy differences are markedly different (It is not meaningful to compare absolute energies obtained with different methods, as difference energy reference values are used. João (talk) 16:51, 10 March 2015 (UTC)). Thus, it is often more efficient to map the potential energy surface using the low level of theory and then to reoptimize at the higher level since it reduces the time required to calculate. It can also be deduced from Table 10 that the distances measured for the chair conformer at both levels of theory are shorter than that for the boat conformer. This is likely due to the greater steric hindrance experienced by the boat conformer, thereby resulting in longer distances.

Table 10: Comparing geometry and energy using HF and DFT method on Chair and Boat TS.
Identity	Chair	Boat
Optimized DFT
Electronic energy	-234.556983	-234.543093
Optimized HF
Electronic energy	-231.619322	-231.602802

The experimental activation energies are 33.5 ± 0.5 kcal/mol via the chair transition structure and 44.7 ± 2.0 kcal/mol via the boat transition structure at 0 K ¹³. The thermochemistry data was obtained for all 3 structures- "Chair" TS, "Boat" TS and the reactant, Anti 2 conformer and summarized in Table 11, below. It was also observed that 1 imaginary frequency remained upon the re-optimization using DFT.

Table 11. Summary of various energies (in Hartree) at HF/3-21G and B3LYP/6-31G*

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466695	-231.461339	-234.556983	-234.414923	-234.408998
Boat TS	-231.602802	-231.450928	-231.445299	-234.543093	-234.402343	-234.396008
Reactant (Anti 2 Conformer)	-231.692535	-231.539539	-231.532567	-234.611711	-234.469219	-234.461869

The tabulated activation energies (using 1 hartree= 627.509 kcal/mol) are represented in Table 12. It can be observed from the table that the activation energy for both the chair and boat pathways decreases upon heating of the system from T = 0 K to T = 298 K. A probable explanation for this occurrence could be due to that the reactant possessing even more accessible vibrational modes than the transition state at higher temperature, thus its potential energy increases significantly more. This increase in potential energy reduces the energy gap between the reactant and transition state, thereby lowering the activation energy.

Table 12. Summary of activation energies (in kcal/mol) at HF/3-21G and B3LYP/6-31G*

	HF/3-21G		B3LYP/6-31G*		Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.70	34.07	33.18	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.97	41.33	44.7 ± 2.0

The data also suggests that the B3LYP/6-31G* level of theory corroborates much better with the experimental values than the HF/3-21G. This is expected since the DFT (B3LYP/6-31G*) method uses a larger basis set and takes into account electron correlation, resulting in better results as compared to the former. It is evident from the relative activation energies that the Cope Rearrangement preferred to proceed via the lower energy chair transition state even though both the chair and boat TS generates the same product.

The Diels-Alder Cycloaddition

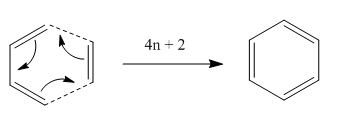
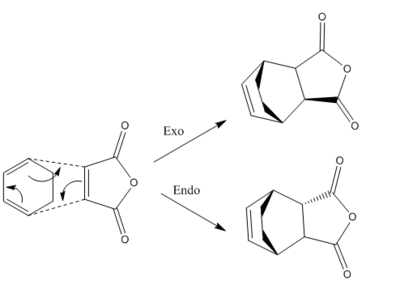
The Diels–Alder reaction is an organic chemical reaction between a conjugated diene and a substituted alkene (dienophile) to form a substituted cyclohexene system. The reaction is an example of a concerted pericyclic reaction and is believed to occur via a single, cyclic transition state. It is common understanding that no intermediates would be generated during the course of the reaction since it undergoes via a concerted fashion ¹⁴. Thus, the Diels–Alder reaction takes orbital symmetry considerations into great account - it is classified as a [4π_S+2π_S] cycloaddition, indicating that it proceeds through the suprafacial/suprafacial interaction of a 4π electron system with a 2π electron system. The HOMO of the diene interacts with the LUMO of the dienophile, resulting in the formation of two new sigma bonds. The formation of new sigma bonds is the driving force of this reaction. This is an interaction that is thermally allowed as a 4n+2 cycloaddition by the Huckel topology and can be illustrated in Figure 12 below ³.


Figure 12. Mechanism of [4+2] Diels-Alder Reaction

The Diels–Alder reaction is a very effective method for generating 6-membered systems with good control over regio- and stereochemical properties. Due to its effectiveness, this reaction has also been applied to other π-systems, such as carbonyls and imines, often used to synthesize the corresponding heterocycles, known as the hetero-Diels–Alder reaction¹⁴.

This part of the exercise involves characterization of transition structures using firstly the lower level of theory, AM1 Semi-Empirical Method (involves Hartree Fock (Not sure what you mean here. Hartree-Fock and AM1 are two distinct methods. João (talk) 17:50, 10 March 2015 (UTC))) and further optimized at the higher level of theory, BLYP3-6-31G* (DFT) method.

Part i

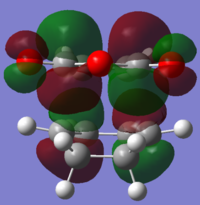
The cis butadiene and ethene molecules were constructed and optimized separately. After which, the HOMO and LUMO of both molecules were plotted. These MOs and their symmetries with respect to plane are represented in Table 13 below.

Table 13: HOMO/LUMO of cis-butadiene and ethene
Identity	HOMO	LUMO
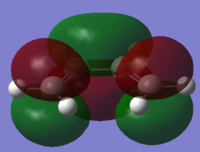
Cis-Butadiene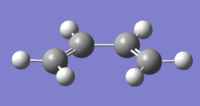
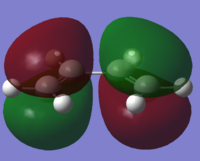Symmetry with respect to plane	Asymmetric (A better description would be anti-symmetric João (talk) 17:50, 10 March 2015 (UTC))	Symmetric
Ethene
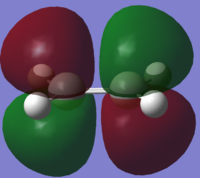Symmetry with respect to plane	Symmetric	Asymmetric

Part ii

This part of the exercise involves computation of the Transition State geometry for the prototype reaction and examination of the nature of the reaction path.

With reference to Table 13, it is evident that the HOMO of the cis-butadiene and LUMO of the ethene are both asymmetric with respect to plane and overlap very well with each other. Therefore, it is the HOMO-LUMO pair that interact in this reaction and the presence of such favourable interaction is the reason why the reaction is allowed to occur. Moreover, it is important to note that the success of pericyclic reaction in this case is governed by the Woodward-Hoffman rules as mentioned previously. The reaction is thermally allowed and takes place suprafacially.

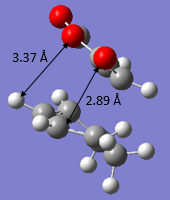
The transition structure has an envelope type structure, which maximizes the overlap between the ethylene π orbitals and the π system of butadiene. The starting geometry was derived by building the bicyclo system and removing the -CH2-CH2- fragment.The guess TS interfragment distance (dashed lines) was then optimized the structure at both AM1 Semi-empirical and BLY3P/6-31G* for comparison.

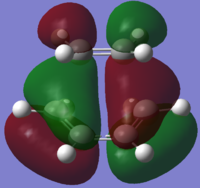
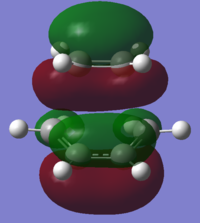
After successful optimization of the correct TS structure, both HOMO and LUMO were plotted and illustrated in Table 14. Referring to Table 14, it can be observed that there is a difference between the HOMO/LUMO plotted using the AM1 Semi-Empirical method and BLY3P/6-31G*. The HOMO plotted using the former method is Asymmetric but Symmetric when the latter was used. Moreover, a slight difference in spatial appearance of the LUMO for BLY3P/6-31G* could be observed compared to that from AM1 Semi-Empirical method.

Table 14: HOMO/LUMO of cis-butadiene and ethene Transition State
MO	HOMO TS	LUMO TS
AM1 Semi-Empirical Method
Symmetry with respect to plane	Asymmetric	Symmetric
DFT (B3LYP/6-31G*)
Symmetry with respect to plane	Symmetric	Symmetric

(How do these orbitals arise? Why are they different? João (talk) 17:50, 10 March 2015 (UTC))

It is important to note that since the transition structure obtained differs slightly for the different methods. This difference is illustrated in Figure 13 and 14 below.

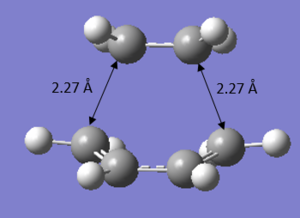
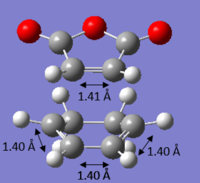
It can be observed from Figure 13 (Semi-Empirical) that all the original C=C double bonds in the original fragments now have a length of 1.38 Å and the original C-C single bond of the butadiene has a bond length of 1.40 Å. This is evident that the double bonds have lost part of their double bond (longer than the typical sp² double bond length of 1.34 Å ¹⁵) character and lengthened towards the single C-C bond length in the product (shorter than typical sp³ single bond length of 1.54 Å ¹⁵). This shows that the transition structures do not possess any formal C-C or C=C bonds, but exist as an intermediate which lies in-between that of both bonds.

It is also evident that the C-C separation between the terminal C carbons of the reacting butadiene and ethene increased from 2.12 Å to a length of 2.27 Å upon calculating at B3LYP/6-31G* level of theory. With understanding that the van der Waals radius of a carbon atom is 1.70 Å and the partially formed σ-bonds are 2.27 Å apart, it is clear that these bonds are longer than the typical C-C bond length but shorter than the total van der Waals radii of both carbons (should be 3.40 Å). Therefore, it is conclusive that overlapping of electron density between the bonding molecular orbitals of both reacting fragments occurred, which enabled bond breaking/forming to proceed in the reaction.


Figure 13. Transition Structure using Semi-Empirical	Figure 14. Transition Structure using DFT

Since it has been previously understood that the transition state differs slightly, it means that the activation energies tabulated via both methods would naturally differ too. The various data obtained from calculations via the two different methods (Semi-Empirical and DFT) could be represented in Table 15 below. The activation energies were then calculated using the Sum of electronic and thermal energies and compared. The activation energy obtained using the AM1 Semi-empirical and DFT method gave a value of 25.50 kcal/mol and 20.53 kcal/mol respectively. It can be concluded that the Semi-empirical AM1 method is more suitable for this particular Diels-Alder cycloaddition since it agrees much better with the experimental values of 25.1 kcal/mol ¹⁶. This is an unexpected occurrence since a higher level of theory (DFT) should effectively give results closer to experimental value. Nonetheless, this could still be possible because reaction between cis-butadiene and ethene is considered a simple reaction and AM1 Semi-Empirical takes into slight account of electron correlation, thus deeming it sufficient to yield a more accurate result compared to that by DFT ¹⁷.

Table 15. Summary of data values based for ethane, cis-butadiene and TS using AM1 Semi-empirical and B3LYP/6-31G* (DFT)


	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies	RMS Gradient Norm	Point Group	No. of imaginary frequencies	Imaginary frequency
Ethene (Semi-Empirical)	0.02619027	0.077198	0.080252	0.081196	0.055660	0.00003328	D_2h	0	N/A
Ethene (DFT)	-78.58745783	-78.536224	-78.533181	-78.532237	-78.557753	0.00014560	D_2h	0	N/A
cis-Butadiene (Semi-Empirical)	0.04879722	0.134553	0.138574	0.139519	0.108518	0.00003500	C_2v	0	N/A
cis-Butadiene (DFT)	-155.98648558	-155.901146	-155.896443	-155.895499	-155.927850	0.00002745	C_2v	0	N/A
DA Transition Structure (Semi-Empirical)	0.11165485	0.253278	0.259455	0.260400	0.224018	0.00003280	C₁	1	-956.17
DA Transition Structure (DFT)	-234.54388540	-234.403328	-234.396905	-234.395961	-234.432903	0.00002408	C₁	1	-526.7587

The vibration of the Diels-Alder transition state is illustrated in the animation shown on the left below, which is expected for that of Diels-Alder cycloaddition. The symmetric movement of the 2 fragments towards each other indicates the synchronised formation of the 2 C-C σ bonds. There is also a lowest vibration reported at frequency 147.39 cm^-1 which possibly represents the twisting of the ethene fragment. This correlates to a asynchronous vibration of the transition state, as shown on the right below. Since this vibration has a positive frequency value, it represents the vibration of the TS and does not contribute to the reaction path.


TS via Semi-Empirical	Vibration of lowest positive frequency

An IRC calcultion was ran both in the forwards and backwards reaction together in one calculation which involves following the minimum energy path from the transition structure down both sides of the transition state maximum to its local minima on a potential energy surface. The calculation was set up to using a maxmimum of 100 steps but both the reactant and product minima were located after 87 steps. The graphical representation is shown below in Figure 14. It can be interpreted from the graph that, from the maximum of the transition state, the calculation follows the minimum energy pathway in the backwards direction to find the reactants, and then in the forwards reaction to find the products. The product minimum is found when the RMS Gradient Norm value reaches 0.000 a.u., which corresponds to a stationary point. The final minimum product is represented in Figure 15, which is what is expected.


Figure 14. IRC pathway recorded


Figure 15. Final product minimum

Part iii

It has been established in Part ii that the AM1 Semi-Empirical method served as a more accurate calculation of the activation energies. However, that could simply be due to to the DA reaction between cis-butadiene and ethene being less complex and so only a lower level of theory is required to give a better calculation. (Simplicity is not a reason for the poor performance of a given method. João (talk) 17:50, 10 March 2015 (UTC))

The regioselectivity of the Diels-Alder reaction between Cyclohexa-1,3-diene and maleic anhydride was investigated in this section. Since this is a more complex DA reaction (compared to that in Part ii, the TS calculations were also carried out at both AM1 Semi-Empirical and DFT method to make substantial comparisons between both methods. In this reaction, it is noted that there are electron-withdrawing oxygen atoms on the dienophile (maleic anhydride) and electron-donating groups on the diene reactant (Cyclohexa-1,3-diene). This favours the cycloaddition more through lowering the energy of LUMO and increasing the energy of the HOMO respectively, allowing for better interaction between both molecular orbitals ¹⁸.

It is understood that the reaction is supposed to be kinetically controlled so that the exo transition state should be higher in energy and the endo TS would be favoured. This Diels-Alder reaction can be represented in Figure 16 as shown below.


Figure 16. Regioselectivity of Diels-Alder reaction between Maleic anhydride and Cyclohexa-1,3-diene

The HOMO and LUMO were plotted for both reactants cyclohexa-1,3-diene and maleic anhydride and represented in Table 16 below. Similar to what was discussed in part ii, the reaction between these 2 molecules are allowed due to good overlap between both orbitals, which is further supported by the HOMO and LUMO argument mentioned earlier.

Table 16: HOMO/LUMO of cyclohexa-1,3-diene and maleic anhydride
Identity	HOMO	LUMO
Cyclohexa-1,3-diene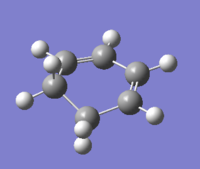
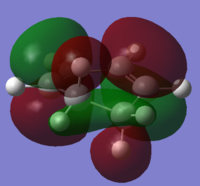Symmetry with respect to plane (Is there a symmetry plane for this structure? João (talk) 17:50, 10 March 2015 (UTC))	Symmetric	Asymmetric
Maleic anhydride
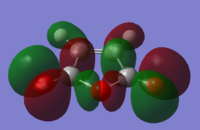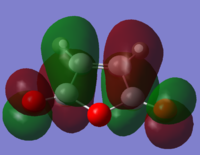Symmetry with respect to plane	Asymmetric	Symmetric

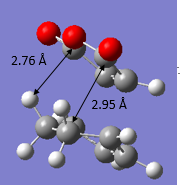
The transition structures for both the Endo and Exo TS were located. This was done by manually setting the reactants to about 2.2 Å apart between the atoms where bond forming occurs and then optimizing the structures to TS(Berny) at both AM1 Semi Empirical and BYLP3/6-31G* level of theory. The bond lengths of the other C-C distances were measured and a sketch with the important bond lengths were shown in Figure 17 and 18 respectively. It is evident from both figures that the bond lengths achieved for both endo and exo transition states were about the same, which is expected - bond lengths of the intermediates is between that of the length of single bond and double bond. The partly formed σ C-C bonds via both the Endo and Exo transition structures were also represented in Table 16 below and it could be observed that the length found in the Exo TS was about 0.00864 Å longer than that of the Endo TS.


Figure 17. Bond lengths for Endo TS	Figure 18. Bond lengths for Exo TS

In addition to investigating the bond lengths, the vibrations of the Endo and Exo transition state are also illustrated in the animation shown below on the left and right respectively. It can be indicated from the symmetric movement of the 2 fragments towards each other that there is a synchronized formation of the 2 C-C σ bonds.


Synchronous vibration by Endo TS	Synchronous vibration by Exo TS

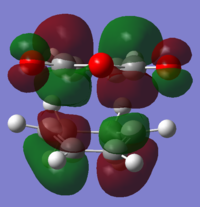
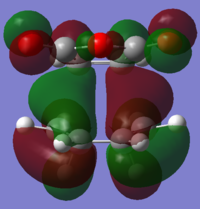
The HOMO and LUMO structures of the both TS were also plotted using both levels of theory and represented in Table 17 below. With careful examination of the nodal properties of the HOMO between the -(C=O)-O-(C=O)- fragment and the remainder of the system, it is observed that there is favourable secondary orbital overlap observed for the HOMO of the Endo TS but not in the Exo TS since the -(C=O)-O-(C=O)- fragment is pointing away from the diene (What is this secondary orbital overlap effect? How does it manifet itself in your results? What should the reader be looking for in the figures? João (talk) 16:30, 11 March 2015 (UTC)). Therefore, the Endo TS is more favourable for the reaction. It can also be observed that the molecular orbitals obtained using both levels of theories appeared to be quite similar (The HOMO for the DFT and AM1 valculation look somewhat different. In fact the structures seem to be different as well. João (talk) 16:30, 11 March 2015 (UTC)), with only slight deviation in the spatial arrangement. This was expected as DFT takes into account even more electron correlation as compared to that of AM1 Semi-Empirical method, thus the HOMO and LUMO structures plotted would be slightly different since different basis sets were taken into account when different levels of theory were used to compute the results. It is also good to note that all the molecular orbitals shown in Table 17 are all Asymmetric to the plane of symmetry.

Table 17: HOMO/LUMO of Endo and Exo TS
	HOMO (Semi-Empirical)	LUMO (Semi Empirical)	HOMO (DFT)	LUMO (DFT)
Endo TS
Symmetry with respect to plane	Asymmetric	Asymmetric	Asymmetric	Asymmetric
Exo TS
Symmetry with respect to plane	Asymmetric	Asymmetric	Asymmetric	Asymmetric

After optimizing the structures, the frequency calculations were also carried out in order to collect sufficient data to understand more about the reacting system, building on theory that we already understand. These values are summarized into Table 18 below. It is important to highlight that the Endo transition state possesses lower amount of energy compared to that of the Exo transition state, making it a more favourable pathway for the Diels-Alder reaction to progress. Using the sum of electronic and thermal energies of the reactants and transition states, the activation energies were calculated for the Endo and Exo TS respectively. The activation energies obtained was 27.68 kcal/mol and 17.33 kcal/mol for the former and 28.46 kcal/mol and 19.92 kcal/mol for the latter, using AM1 Semi-Empirical and DFT method respectively. There are two conclusions formed from these values. Firstly, the DFT method gave activation energies that corroborate better with the literature value of 11.4 kcal/mol ¹⁹ which meant that it was a more accurate method for this particular example. This was not entirely surprising because DFT is an even higher level of theory compared to that of AM1 Semi-Empirical method, utilizing even larger basis set and taking into account electron correlation. Secondly, it is clear that the Endo TS requires a lower activation energy than the Exo TS, deeming Endo TS a more kinetically favoured route for this Diels-Alder reaction.

Table 18. Summary of data values based for Maleic anhydride, Cyclohexa-1,3-diene and TS using Semi-empirical (AM1) and B3LYP/6-31G* (DFT)


	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies	RMS Gradient Norm	Point Group	No. of imaginary frequencies	Imaginary frequency
Cyclohexane-1,3-diene (Semi-Empirical)	0.02771128	0.152502	0.157726	0.081196	0.158670	0.123833	C₂	0	N/A
Cyclohexane-1,3-diene (DFT)	-233.41891187	-233.296117	-233.290938	-233.289994	-233.324375	0.00000659	C₂	0	N/A
Maleic Anhydride (Semi-Empirical)	-0.12182415	-0.063348	-0.058194	-0.057250	-0.092500	0.00007336	C_2v	0	N/A
Maleic Anhydride (DFT)	-379.28953533	-379.233650	-379.228468	-379.227524	-379.262720	0.00011179	C_2v	0	N/A
Endo Transition Structure (Semi-Empirical)	-0.05149527	0.133495	0.143684	0.144628	0.097353	0.00014070	C₁	1	-806.5208
Endo Transition Structure (DFT)	-612.68339623	-612.502142	-612.491788	-612.490844	-612.538330	0.00002990	C₁	1	-447.2677
Exo Transition Structure (Semi-Empirical)	-0.05041938	0.134880	0.144881	0.145825	0.099116	0.00002028	C₁	1	-811.8458
Exo Transition Structure (DFT)	-612.67929694	-612.498012	-612.487661	-612.486717	-612.534265	0.00000809	C₁	1	-448.4461

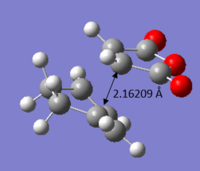
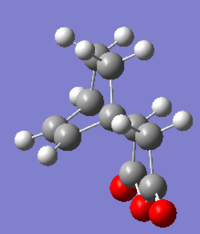
Finally, the orientation, (C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- for the exo and the “opposite” -CH=CH- for the endo) were investigated. With reference to the Endo and Exo through-space distances illustrated in Figures 19 and 20 respectively, it can be observed that the through space distance for the Endo is 0.06 Å shorter than that of the distance measured in the Exo TS. It is evident from the figures that the Exo TS experiences greater steric repulsion as compared to that of the Endo TS due to the hydrogen atoms and the -(C=O)-O-(C=O)- group being in closer proximity, thereby causing making the Exo TS more unstable. This is also evident from the electronic energies of the Endo TS possessing lower amount of energy of 90.16 kcal/mol compared to that of Exo TS of 90.92 kcal/mol, making the former TS a more stable conformer. Moreover, the former is also more favoured transition state due to it being a kinetically preferred (Is that a consequence or a cause for the lower activation energy? João (talk) 16:30, 11 March 2015 (UTC)) and also because of the stabilizing secondary orbital overlap effect present in the Endo TS.


Figure 19. Through space distance for Endo TS	Figure 20. Through space distance for Exo TS

After the Endo and Exo transition structures were achieved, the IRC was performed on the respective structures to generate both product minimum as illustrated in Figure 21 and 22 respectively. Both products obtained were what we would expect from athe Endo and Exo TS respectively.


Figure 21. Endo product	Figure 22. Exo product

Further Discussion

Some effects were neglected in the calculations of Diels Alder transition states. These factors included that of solvent effects that would affect the results obtained. Based on a literature paper ²⁰ that investigates effects of dynamical solvation effects, it was understood that the inclusion of water molecules result in four different effects - flattened potential energy near the transition state, curvature peaks located close to the transition state and larger in magnitude and finally lowered frequencies of relevant orthogonal vibrational modes near the transition state. All these effects have minimal effect the transmission coefficient but lowers the free energy barrier significantly ²⁰.

The study of solvent effects for the Diels-Alder reaction takes into account the importance of nature of dynamical solvent effects as well as the water molecules' structure and electrostatic roles. It is important to take these effects into account when calculating the reactions such as Diels-Alder cycloaddition since reactions for different molecules may take place in different solvents which will directly affect the results obtained.

Conclusion

In conclusion, it was observed that various conformers of 1,5-Hexadiene molecule was successfully optimized since the electronic energy calculated for all the conformers corroborated well with the values stated in Appendix 1. It was also noted that there is a correlation between the number of s-cis C_sp² - C_sp³ bonds and the molecule energy, whereby the greater the number of bonds, the higher the energy level due to more prominent steric hindrance. Moreover, it was concluded that presence of CH/π attractive interaction led to stability of the Gauche 3 conformer. It was also established from this exercise that the higher level of theory, B3LYP/6-31G* (DFT) is a very effective method in yielding good calculation results. This is greatly attributed to the fact that electron correlation is accounted for and also due to a larger basis set used for calculations, thereby leading to more accurate results.

It was evident through the optimization of the chair transition state that both Hessian and Frozen Coordinate Method worked well and gave similar optimized structures at the HF/3-21G level of theory. However, the frozen coordinate method works more effectively when the guess structure deviates largely from the actual transition structure. For the optimization of boat transition state, it was noted that QST2 was an effective method but required the geometries of the reactant and product molecule to bear a resemblance to the boat transition structure or the calculation would fail. The QST3 method utilized was also successful as the reactant and product converged to generate the optimized boat structure. The IRC method used to identify the product minimum was useful but required further optimization to enable the real minimum structure to be achieved. It can also be concluded from the activation energies calculated using HF and DFT that the latter gave values that agreed more with the literature values. Moreover, the chair conformer was preferred due to its stability and lower activation energy required.

The Diels-Alder reaction between ethane and cis-butadiene were successfully carried out and it can be concluded that the AM1 Semi-Empirical method worked better compared to the higher level of theory, B3LYP/6-31G* (DFT). A probable explanation for this occurrence could be due to the reaction being quite straightforward. Moreover, with AM1 Semi Empirical accounting for some electron correlation, a better calculation was achieved. Finally, the reaction of a more complex cycloaddition was investigated between maleic anhydride and cyclohexa-1,3-diene. It can be concluded from the various geometries and energies obtained that the Endo TS has favourable secondary orbital overlap effect and less steric repulsion. Moreover, it was also the kinetically favoured pathway. Additionally, the B3LYP/6-31G* (DFT) level of theory yielded activation energies that agreed better with literature.

The various reactions could be investigated further by taking into account solvent effects and comparing those values with those obtained in this exercise.

References

1. P M.W. Gill, Adv in Quantum Chem, 1994, 25, 141–205.

2. J. Fernández Rico, R. López, G. Ramírez and I. Ema, J. Comput. Chem.,2001, 22, 1655–1665.

3. R. B. Woodward, R. Hoffmann, J. Am.Chem. Soc., 1965, 87, 395.

4. J J. Blavins, D L. Cooper and P B. Karadakov, J. Phys. Chem. A, 2004, 108, 194-202.

5. D J. Tantillo and R. Hoffmann, J. Org. Chem., 2002, 67, 1419-1426.

6. B W. Gung, Z. Zhu, and R A. Fouch, J. Am. Chem. Soc., 1995, 117, 1783-1788.

7. M. Nishio, M. Hirota, Y.Umezawa, “The CH/π Interaction: Evidence, Nature, and Consequences”, USA, Wiley-VCH, 1998, 93.

8. M. J. Bearpark, A. Simperler, 'Lecture 3: Calculating Energies: Methods/Basis Sets/Spin States', QM3 Quantum Mechanics 3/Core 3rd Year Computational Chemistry Laboratory, 21/10/2014, Imperial College London.

9. A. Szabo, N. S. Ostlund, “Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory”, Mineola, New York, Dover Publishing, 1996.

10. M. J. Bearpark, A. Simperler, 'Lecture 1: Calculating Molecular Geometries’, QM3 Quantum Mechanics 3/Core 3rd Year Computational Chemistry Laboratory, 14/10/2014, Imperial College London.

11. Imperial Chemistry Wiki, https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3

12. R.M. Silverstein, G.C. Bassler and T.C. Morrill, “Spectrometric Identification of Organic Compounds”, 4th ed. New York, John Wiley and Sons, 1981.

13. K. J. Shea and R. B. Phillips, J. Am. Chem. Soc., 1980, 102, 3156-3162.

14. K. C. Nicolaou, Scott A.. Snyder, Montagnon, T. Vassilikogiannakis and G. Vassilikogiannakis, "The Diels-Alder Reaction in Total Synthesis", 2002. Ang. Chem. Int. Ed., 41, 1668.

15. J. M. Baranowski, J. Phys. C: Solid State Phys., 1986, 19, 4613-4621.

16. D. Rowley and H. Steiner, Discuss. Faraday Soc., 1951, 10, 198-213.

17. W. Thiel, “Theory and Applications of Computational Chemistry: The First Forty Years”, Chapter 21, Elsevier, 2005, 559- 580.

18. F A. Carey, R J. Sundberg, “Advanced Organic Chemistry: Part A: Structure and Mechanisms”, New York, Springer, 2008, 847.

19. C. A. Eckert., R. A. Grieger., J. Am. Chem. Soc., 1970, 92, 7149–7153

20. H. Hu, M N. Kobrak, C. Xu, and S. Hammes-Schiffer, J. Phys. Chem. A, 104, 8065-8066