Module 3

The Cope Rearrangement Tutorial


Figure 1: [3,3] sigmatropic Cope rearrangement of C₆H₁₀

The aims of this tutorial are:

To find the intermediates and transition states (TS)
To deduce the favoured reaction pathway
To calculate activation energies, enthalpies, vibrational frequencies and force constants

Optimising the Reactants and Products

The 1,5-hexadiene structure, antiperiplanar for the four central C atoms, was cleaned and optimised using the Hartree-Fock (HF) method and 3-21G basis set with 250 MB memory limit. The optimised structure in the .chk file had an energy of -231.69260 a.u. and C₂ symmetry. This was the anti1 conformer.

Next, another molecule of 1,5-hexadiene, gauche for the four central C atoms, was optimised at the HF/3-21G level of theory. This structure had an energy of -231.68962 a.u., slightly higher than the anti structure, and this time the molecule had no symmetry. This was the gauche5 conformer. The gauche structure is less stable than the anti structure, due to steric strain between the two freely rotatable bulky groups at close proximity.


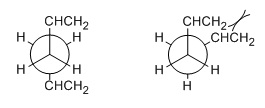
Figure 2: Anti (left) and gauche (right) Newman projections

The conformation of 1,5-hexadiene with the lowest energy was the gauche3 conformer, with an energy of -231.69266 a.u.

The C_i anti2 conformation of 1,5-hexadiene was optimised at the HF/3-21G level of theory. Its final energy was calculated to be -231.69254 a.u., lit. -231.69254 a.u. The structure was then reoptimised at the B3LYP/6-31G* level, and the energy was found to be -234.55970 a.u. The overall geometries of the final structures from the HF/3-21G calculation and the B3LYP/6-31G* level of theory were compared.

Table 1: Geometries of structures from HF/3-21G and B3LYP/6-31G*

		HF/3-21G	B3LYP/6-31G*
Bond length/Å	C=C	1.32	1.34
	C-C	1.51	1.51
	C3-C4	1.55	1.56
Bond angle/°	C=C-C	124.8	125.2
	C-C-C	111.3	112.7
Dihedral angle/°	C=C-C-C	114.7	118.7
	C-C-C-C	180.0	180.0

The overall geometry did not change very much. A frequency calculation was run at the same level of theory. All the vibrational modes had real frequencies.

Table 2: Energy and enthalpy of Cope rearrangement (a.u.)

E_elec + ZPE	-234.416252
E + E_vib + E_rot + E_trans	-234.408952
E + RT	-234.408008
H - TS	-234.447896

Optimising the "Chair" and "Boat" Transition Structures

An allyl CH₂CHCH₂ fragment was optimised using the HF/3-21G level of theory. Two optimised allyl fragments were orientated into the chair TS, with both fragments approximately 2.20 Å apart. TS optimisations were then set up using Methods I and II:

Method I The TS was optimised (Opt+Freq) to TS (Berny) and the force constants were calculated once (Opt=NoEigen). The calculation gave an imaginary frequency (-818 cm^-1) and it corresponded to the C-C bond breaking and forming in the Cope rearrangement.

Method II The redundant coordinate editor was used to freeze the coordinates of the bonds between the two pairs of terminal Cs of the fragments that would break or form during the rearrangement. The TS was then optimised again. The optimised structure in the .chk file was taken and the redundant coordinate editor was used to differentiate the bonds between the same two pairs of terminal Cs of the fragments. The TS was once again optimised but the force constants were not calculated. The bond-breaking or bond-forming bond lengths were 1.55 and 4.39 Å, compared to 2.02 and 2.02 Å in the one optimised in Method I.

The atoms in the optimised C_i reactant and product molecules were numbered in the same way. Both molecules were optimised (Opt+Freq) to TS (QST2) and the chair TS was formed. In the original input file that was set up for QST2 calculation, for both the molecules, the C-C-C-C dihedral angle was set to 0° and the C-C-C bond angles were reduced to 100°. The QST2 calculation was set up again and the boat TS was formed. There was only one imaginary frequency calculated (-839 cm^-1) and it corresponded to the C-C bond breaking and forming in the Cope rearrangement.

From the .chk file of the optimised chair TS, the Intrinsic Reaction Coordinate (IRC) method was used to compute in the forward direction over 50 points, calculating the force constants once. From there, three approaches were taken:

Approach (i) The last point on the IRC was taken and minimised. This gave a minimum geometry and converged to the C₂ gauche1 conformation.

Approach (ii) The IRC was restarted with 60 and 100 points. However, this did not give a minimum geometry.

Approach (iii) The IRC was redone and the force constants were computed at every step. However, this also did not give a minimum geometry.

The HF/3-21G optimised chair and boat TS were reoptimised at the B3LYP/6-31G* level of theory (Opt+Freq). The geometries and energy differences between the reactants and TS at the HF/3-21G and B3LYP/6-31G* levels of theory were compared. The bond lengths were closely matched, but B3LYP/6-31G* gave energy differences that were much smaller than those from HF/3-21G. Other than the anomalous value for ΔE (chair) from HF/3-21G, the computed values are on the average within ±0.1 of the experimental values.

Table 3: Summary of geometries and energy differences

	HF/3-21G			B3LYP/6-31G*
	Reactant	Boat TS	Chair TS	Reactant	Boat TS	Chair TS
CC bond lengths/Å	1.32	1.38	1.38	1.34	1.40	1.41
	1.51	1.38	1.38	1.51	1.40	1.41
	1.58	2.14	3.29	1.58	2.25	2.04
ΔE at 0 K /kcal mol^-1	-	50.3	105	-	36.6	28.7
Expt. ΔE /kcal mol^-1	-	44.7 ± 2.0	33.5 ± 0.5	-	44.7 ± 2.0	33.5 ± 0.5

The Diels Alder Cycloaddition


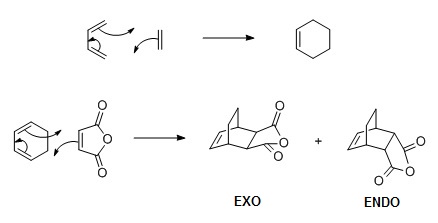
Figure 3: Cycloaddition of butadiene with ethylene (top) and cyclohexadiene with maleic anhydride (bottom)

The aims of this exercise are:

To characterise the TS and study the TS geometry and molecular orbitals (MOs)
To examine the nature of the reaction path
To study the regioselectivity of the Diels Alder cycloaddition

The nature of the TS for the Diels Alder reaction is also studied for when the diene and dienophile carry substituents, and when secondary orbital effects are possible.

The interaction of the π orbitals comprise three π_C=C → π*_C=C. Two σ bonds are made on the same side of the π ring (suprafacial). π orbitals interact with each other if they are in phase. Otherwise, a node or nodal plane is formed between them.

Cis Butadiene

Cis butadiene was optimised at the HF/3-21G level of theory and the Highest Occupied MO (HOMO) and Lowest Unoccupied MO (LUMO) were plotted. The former was anti-symmetric (a) and the latter was symmetric (s) with respect to plane.


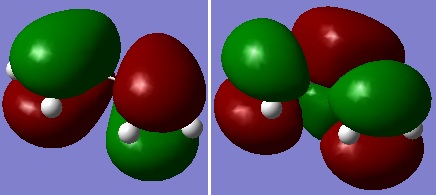
Figure 4: HOMO (left) and LUMO (right) of cis butadiene

Computation of the Transition State Geometry and Examination of the Reaction Path

The bond lengths and angles of the TS, from the cycloaddition of cis butadiene and ethylene, were adjusted according to literature values.^[1] The structure was then optimised (Opt+Freq) to a TS (Berny), calculating force constants once, at the HF/3-21G level of theory (Opt=NoEigen) [DOI:10042/to-13734 ]. There was an imaginary vibrational frequency (-818 cm^-1), thereby confirming that a TS was obtained. This lowest and negative frequency was synchronous and corresponded to the TS reaction path. The HOMO and LUMO (both s) of the TS were plotted. The LUMO of butadiene and HOMO of ethylene have been used to form the HOMO of the TS. The reaction is allowed, because the LUMO of butadiene and HOMO of ethylene have the same symmetry, i.e. both are s leading to the resultant TS also being s.


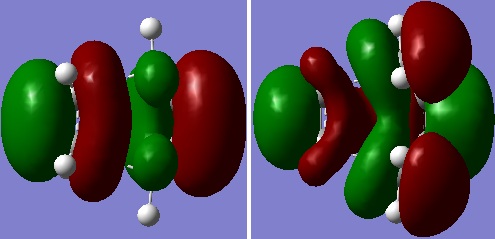
Figure 5: HOMO (left) and LUMO (right) of TS


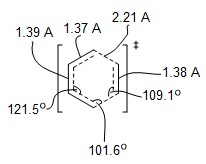
Figure 6: Geometry of TS

Typical sp³ and sp² C-C bond lengths are 1.54 and 1.34 Å respectively. The van der Waals radius of the C atom is 1.70 Å. The C-C bond length of the partly formed σ C-C bonds in the TS closely matches that of an sp³ C-C bond. There is a large overlap of van der Waals radii between the terminal Cs of the diene and dienophile fragments in the TS.


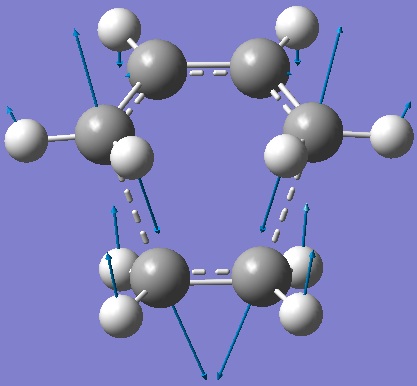
Figure 7: Vibration corresponding to the TS reaction path

The formation of the two bonds is synchronous, unlike the lowest positive frequency (166 cm^-1) which is asynchronous.

Study of the Regioselectivity of the Diels Alder Reaction

The pairs of C-C bonds that form in both the endo and exo TS, from the Diels Alder reaction of cyclohexadiene with maleic anhydride, were adjusted to 2.2 Å. The endo and exo TS were located by optimising (Opt+Freq) to a TS (Berny), calculating force constants once, at the HF/3-21G level of theory (Opt=NoEigen) [DOI:10042/to-13758 ; DOI:10042/to-13763 ]. The endo and exo TS had one imaginary frequency each (-643 and -647 cm^-1 respectively) and corresponded to the TS reaction path, so a TS had been reached. The endo TS (-605.61 a.u.) had a lower energy than the exo (-605.60 a.u.). The endo form has the -(C=O)-O-(C=O)- fragment of the dienophile pointing inward towards the diene, while the exo form has that fragment pointing outward away from the diene.


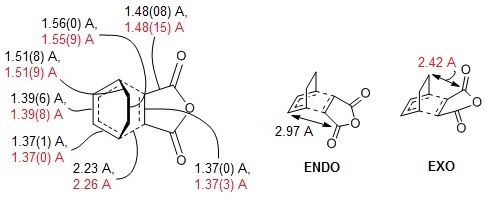
Figure 8: CC bond lengths of both endo and exo TS (left, black: endo, red: exo) and through-space distances (right)

The exo form is more strained than the endo form. This could be because the exo form has a smaller through-space distance, so the steric strain of the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the opposite atoms is greater.


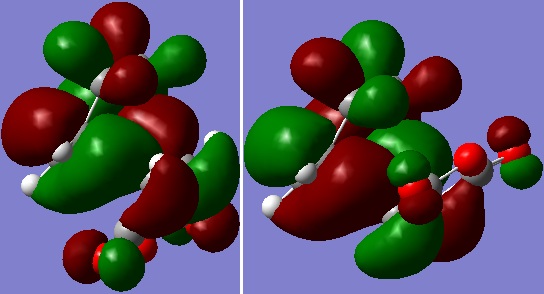
Figure 9: HOMOs of endo (left) and exo TS (right)

The HOMOs of endo and exo TS were mapped, both of which are a. Judging from the nodal properties of the HOMOs, there did not seem to be any significant secondary orbital overlap.

The effects which have been neglected in these calculations of the Diels Alder TS include:^[2]

Dipole-dipole interactions (affecting the approach of the diene and dienophile)
Regioselectivity (preference for one site of cycloaddition in the presence of other sites)
Catalysts (Lewis acid catalysts increase regioselectivity)
Electron-electron and nuclear-nuclear repulsions (disfavour the diene and dienophile coming together)^[3]
Solvation effects (lowering the activation energy barrier)^[4]

References

↑ S.M. Bachrach and M. Liu, J. Org. Chem., 57, 6736 (1992) [DOI:10.1021/jo00051a013 ]
↑ I. Fleming, Molecular Orbitals and Organic Chemical Reactions (Wiley, 2010)
↑ P. Caramella, K.N. Houk and L.N. Domelsmith, J. Am. Chem. Soc., 99, 4511 (1977) [DOI:10.1021/ja00455a056 ]
↑ H. Hu, M.N. Kobrak, C. Xu and S. Hammes-Schiffer, J. Phys. Chem. A, 104, 8058 (2000) [DOI:10.1021/jp000449e ]

[1] S.M. Bachrach and M. Liu, J. Org. Chem., 57, 6736 (1992) [DOI:10.1021/jo00051a013 ]

[2] I. Fleming, Molecular Orbitals and Organic Chemical Reactions (Wiley, 2010)

[3] P. Caramella, K.N. Houk and L.N. Domelsmith, J. Am. Chem. Soc., 99, 4511 (1977) [DOI:10.1021/ja00455a056 ]

[4] H. Hu, M.N. Kobrak, C. Xu and S. Hammes-Schiffer, J. Phys. Chem. A, 104, 8058 (2000) [DOI:10.1021/jp000449e ]

[1]

[2]

[3]

[4]