Rep:Mod:jb4109(2)

Module 2

Optimising a Molecule of BH₃

A molecule of BH₃ was optimised. The gradient is the slope of the potential energy-distance graph, and a gradient less than 0.001 a.u. (Table 1) showed that the optimisation was complete. The "real" text-based .log file output was also checked to ascertain that the forces and displacements had converged.

Table 1: General information of optimisation of BH₃

Optimised B-H Bond Distance	1.19 Å
Optimised H-B-H Bond Angle	120.0o
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Final Energy	-26.5 a.u.
Gradient	4.51 x 10-5 a.u.
Dipole Moment	0.00 D
Point Group	D3h
Calculation Time	6.0 s

Table 2: Vibrational modes of BH₃

No.	Form of vibration	ν/cm-1	Intensity	Symmetry D3h point group
1	All H atoms move up and down together, B atom moves up and down, but opposite direction to H atoms	1146.03	92.7	A2"
2	Two H atoms move back and forth sideways in a concerted scissor-like motion	1204.86	12.4	E'
3	Two H atoms move back and forth sideways in a scissor-like motion, remaining H atom moves sideways	1204.86	12.4	E'
4	All H atoms move in and out together, B atom is stationary	2591.65	0.0	A1'
5	One H atom moves in while another H atom moves out concertedly	2730.07	103.8	E'
6	One H atom moves in while the other two H atoms move out concertedly	2730.07	103.8	E'

Figure 1: Infrared (IR) spectrum of BH₃

There are fewer than six peaks in the spectrum (Figure 1) even though there are six vibrations (Table 2), because the vibration at 2591.65 cm^-1 has zero intensity, the two vibrations at 1204.86 cm^-1 are degenerate, and the two vibrations at 2730.07 cm^-1 are also degenerate. Hence, only three peaks are shown in the spectrum.

Using .chk file for the optimised BH₃ molecule, a Full Natural Bond Orbital (NBO) analysis was performed ("pop=full"). [DOI:10042/to-13089 ] In the Formatted Checkpoint File, the occupied Molecular Orbitals (MOs) and Lowest Unoccupied Molecular Orbital (LUMO) were visualised (Figure 2). The .log file was then analysed for the NBO, and the charges are +0.3 and -0.1 for the B and H atoms respectively.

Figure 2: MO diagram of BH₃

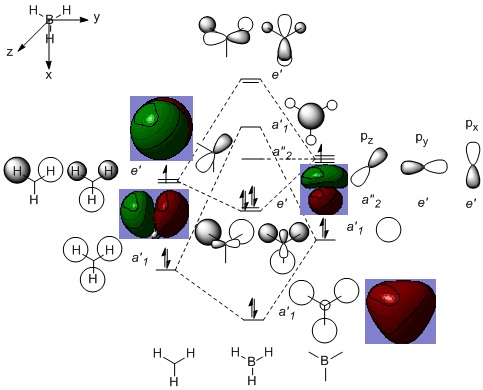
There are no significant differences between the real and Linear Combination of Atomic Orbtials (LCAO) MOs. The qualitative MO theory is useful in predicting the shapes, polarities and general relative energy levels of the MOs, but does not accurately reflect the specific energy levels and exact energy differences between the MOs. Gaussian computed BH₃ with eight valence electrons, instead of six, so when the MOs were generated, there were four occupied MOs instead of three. The lowest occupied MO generated by Gaussian was ignored, because it was a lone pair of electrons occupying a boron sAO.

Using Pseudo-potentials and Larger Basis Sets for TlBr₃

A molecule of TlBr₃ was optimised with restricted D_3h symmetry and a high tolerance value of 0.0001 (Table 3).

Table 3: General information of optimisation of TlBr₃

Optimised Tl-Br Bond Distance	2.69 Å, lit. 2.56 Å
Optimised Br-Tl-Br Bond Angle	120.0o
File Type	.log
Calculation Type	SP
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Final Energy	-91.2 a.u.
Gradient	8.80 x 10-7 a.u.
Dipole Moment	0.00 D
Point Group	D3h
Calculation Time	31.0 s

The same method and basis set must be used for both calculations for energies to be compared, because the total energies of molecules are easily affected by these parameters. A frequency analysis has to be carried out to confirm that the optimised structure is a minima. The "low frequencies" for TlBr₃ are: -3, -0.003, -0.0004, 0.002, 4, 46, 52 cm^-1. The lowest "real" normal mode has a frequency of 46 cm^-1 and 4 cm^-1 in the infrared. Sometimes gaussview does not draw the bonds where expected, because the interatomic distance is greater than what the program has determined beforehand. A chemical bond is the electrostatic force of attraction force of one atom with another within a molecule. A covalent bond is the sharing of electron pairs between atoms. An ionic bond is Coulombic attraction between a cation and anion.

Isomers of Mo(CO)₄L₂

The ground state structures of cis- and trans-Mo(CO)₄(PCl₃)₂ were optimised using the B3LYP method and LANL2MB basis set with loose convergence criteria ("opt=loose"). The torsional angles of the PCl₃ ligands were changed in order to get to the lowest energy minima. The isomers were then optimised using the B3LYP method and LANL2DZ basis set with increased electronic convergence ("int=ultrafine scf=conver=9"). [Cis DOI:10042/to-12904 ; trans DOI:10042/to-12905 ]

The IR frequencies were calculated with the B3LYP method, LANL2DZ basis set and increased electronic convergence. [Cis DOI:10042/to-12939 ; trans DOI:10042/to-12938 ] Bond lengths: Mo-P 2.51 Å (cis), 2.44 Å (trans), lit. 2.42 Å; Mo-C 2.06 Å (both cis and trans), lit. 2.04 Å. In the cis isomer, the Mo-P bonds are longer and weaker due to steric repulsion between the two PCl₃ ligands at close proximity. Relative energies: -0.237(5080) kJ/mol (cis), -0.237(5076) kJ/mol (trans). The trans isomer is slightly more stable. This is because it has both PCl₃ ligands far apart from each other as much as possible, so steric strain is minimised. The energy difference between these isomers is small (4 x 10^-7 kJ/mol). We can use the ligand L = PH₃, which has a smaller steric bulk, to try and stabilise the cis isomer. None of the vibrations have a very low or negative frequency (Figure 3).

Figure 3: Displacement vectors of low-frequency vibrations of cis- (top) and trans-Mo(CO)₄(PCl₃)₂ (bottom)

The low frequency vibrations and rotations correspond to the molecule breathing, torsional and hindered rotational modes at room temperature. The IR spectral assignments are shown in Table 4 below. The experimental values were taken from 2nd year lab (Identification of Stereochemical Isomers of [Mo(CO)₄L₂] by Infrared Spectroscopy).

Table 4: IR spectra of cis and trans isomers

	Cis (cal.)	Cis (exp.)	Trans (cal.)	Trans (exp.)
ν/cm-1	1945, 1949, 1958, 2024	1865, 1892, 1925, 2025	1951, 1951, 1978, 2031	1892, 2013, 2028

The cis isomer has vibrations of a slightly lower frequency than the trans isomer. Two of the vibrations of the trans isomer are degenerate, therefore the number of bands predicted from symmetry is correctly reflected in the experimental IR spectra.

Mini Project: Explore Bonding in Main Group Halides

The aim of this mini project is to:

• Determine the stability of the isomers of Al₂Br₂Cl₄
• Investigate the effect of the Br atoms on the vibrational motion of the molecule
• Visualise the MOs of Al₂Br₂Cl₄

Isomers of Al₂Br₂Cl₄: I [AlCl₂(µ-Br)₂AlCl₂, jmol file, DOI:10042/to-12989 ], II [AlBr₂(µ-Cl)₂AlCl₂, jmol file, DOI:10042/to-12990 ], III [trans-AlBrCl(µ-Cl)₂AlClBr, jmol file, DOI:10042/to-12991 ], were optimised with the B3LYP method and 6-31G(d) basis set. A frequency analysis was then performed to confirm that all three isomers have a minimum, i.e. all positive vibrational frequencies.

Relative energies: -2.84(49994) kJ/mol (I), -2.84(49976) kJ/mol (II), -2.84(49975) kJ/mol (III). The differences in energies is really miniscule. The lower the energy, the more stable the molecule is. Therefore, isomer I is most stable, followed by isomer II, and then followed by isomer III. From the similarity in energies between isomers II and III, it can be seen that stability has something to do with the bridging halogens. Isomer I is most stable, because the bridging Br atoms have a more diffuse electron cloud, and so can form stronger dative bonds to the Al atoms.

Figure 4: Isomer geometries

The data for terminal and bridging bond lengths agree with each other across the three isomers (Figure 4). It can be seen that bridging Al-X bonds are longer than terminal Al-X, because 3c-2e bonds are weaker than 2c-2e bonds.

Table 5: Isomer vibrational frequencies (cm^-1)

	I	II	III	Lit.,
Terminal Al-Cl	471, 602	534, 609	585	484, 625
Terminal Al-Br	-	413, 503	412	373, 500
Bridging Al-Cl	-	417	430	420
Bridging Al-Br	255, 366	-	-	198, 341

The vibrational frequency is inversely proportional to the square root of the reduced mass. Because Br (red atom) has a bigger atomic size than Cl (green atom), so the Al-Br vibrations has a smaller frequency than the Al-Cl vibrations (Table 5). This can also be seen from the smaller displacement vectors that the Al-Br vibrations have compared to the Al-Cl vibrations.

Figure 5: HOMO-6 (top left) to LUMO+1 (bottom right) of isomer I [DOI:10042/to-13019 ]

Figure 6: HOMO-6 (top left) to LUMO+1 (bottom right) of isomer II [DOI:10042/to-13020 ]

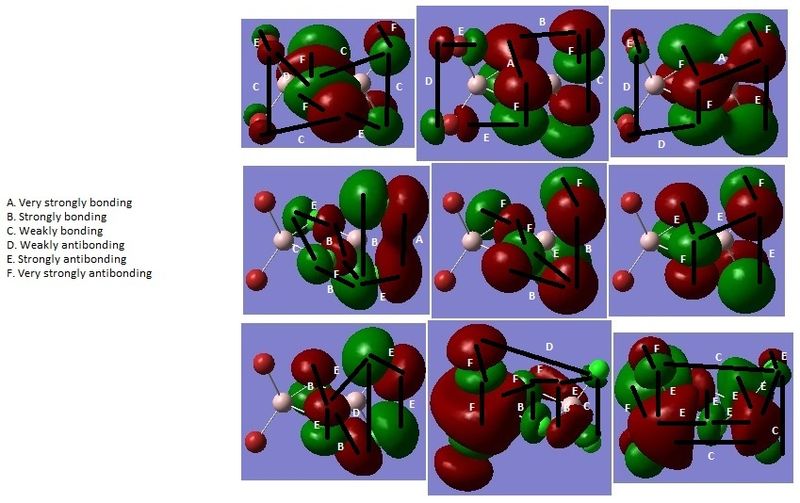
Figure 7: HOMO-6 (top left) to LUMO+1 (bottom right) of isomer III [DOI:10042/to-13021 ]

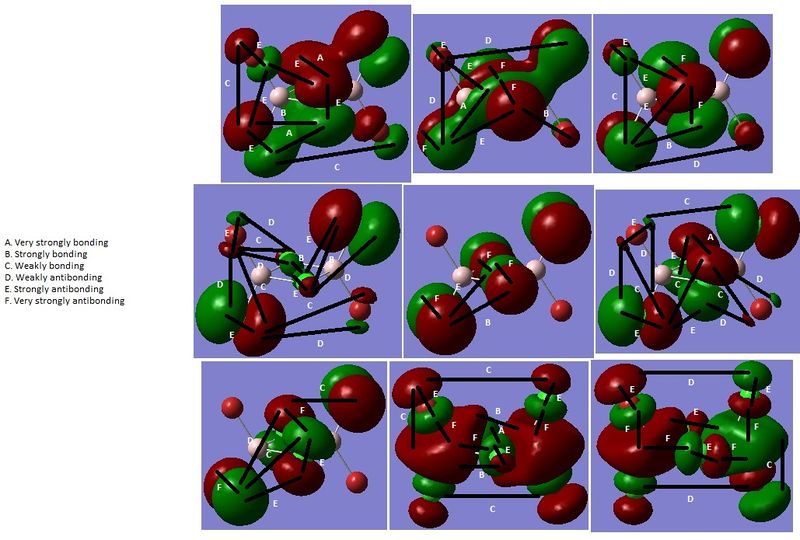
The LUMOs are more diffuse, and have more nodes, than the HOMOs (Figures 5-7).

Figure 8: Atomic charges of isomers

An NBO analysis was carried out, and the NBO charges are shown in Figure 8 above. A bridging halogen atom has a smaller negative charge than a terminal halogen atom, because in a bridging halogen atom, the two electrons are spread out over three atomic centres. Cl is more electronegative than Br, so the Cl atom has a greater negative charge than the Br atom. Consequently, an Al atom connected to four Cl atoms has the greatest positive charge, i.e. Al2 of isomer II (+1.4).

In conclusion:

• AlCl₂(µ-Br)₂AlCl₂ is the most stable isomer, because of a larger electron cloud of the bridging Br, so stronger dative bonding to Al.
• ν(Al-Br) is smaller than ν(Al-Cl), because Br is a bigger atom.
• The MOs of Al₂Br₂Cl₄ isomers were mapped and analysed.