Rep:Mod:janiemac

Nanme: Genco Devrim Barikan, CID: 00610085, Yr3 Computational Labs, Module 3

Introduction

It is often difficult to study the behavioural features of transition states as they are species that exhibit a short half-life, which makes it a challenge to trap them. Such states can be studied extensively in the context of heavy-light-heavy atom interactions, as this scenario creates a locked-in entropy and the species recross the saddle point on the potential energy surface multiple times. This is what is seen in the interaction of an H-I atom with an additional Iodine; TS[I----H----I]#.^[1] However, this is not always observed, and such structures often require spectroscopic information that can only be obtained at a femtosecond timescale.

Given the challenging nature of these short-living species, it is possible to rely on computational methods as an alternative mean to calculate the relative energies of these systems and reach viable conclusions. This study investigates two relevant systems; namely the Cope rearrangement of 1,5-hexadiene and a regioselective Diels-Alder reaction. Precursors to both the reactions have been provided as a backdrop, and the calculations of these precursors afford additional information regarding transition state stabilities and reactivities.^[2]

The Cope Rearrangement

Overview

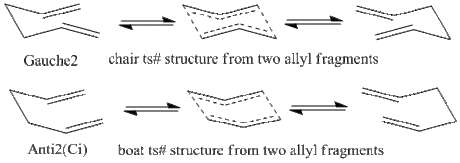
The Cope rearrangement, initially found and described by Arthur Cope, describes the [3,3]-sigmatropic rearrangement that is observed in dienes species where the two alkenes exhibits 1,5- connectivity. An example is shown on the right, where n-1,5-hexadiene undergoes Cope rearrangement to afford the identical 1.5-hexadiene.

It is worth noting that the rearrangement is reversible, however the equilibrim in the context of 1,5-hexadiene can be thought to be equal in the forward and reverse sense, as the stability of the products are equal.

The reaction is well known to proceed via a loose-aromatic structure, where the ts# can adopt either a chair or a boat conformation. The purpose of this study is to investigate these two transition structures and obtain reasonable data to reach a viable conclusion.^[3]^[4]^[5]^[6]

Optimising the Reactants & the Products

The Cope rearrangement of 1,5-hexadiene is considered to undergo via a loosely-bound aromatic transition structure. The relative conformational flexibility of a C6-molecule is evident, and it is well known that such a system would either prefer to adopt either a chair or a boat structure. This gives much insight to the reaction pathway, however, in order to determine the correct pathway, both the structures and also their conformational perturbations must be studied energetically.

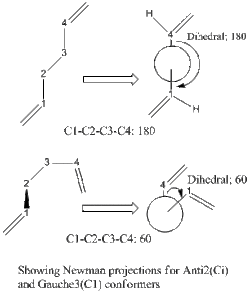
Given the aliphatic nature of the hexa-alkane structure, two initial Newman projections come to mind, the two being the -anti and -gauche linkages. An example of the Newman projections for Anti2 and Gauche3 have been given on the right. These are applied to the central 4-Carbons, and perturbations were obtained. The geometries can be displayed in the table given below.

The calculations tabulated below are given for analysis, as well as future reference and comparison when the correct lowest energy conformer is obtained via an IRC calculation.

Table 1.1 "HF/6-21G Energy calculations for 10 conformations of 1,5-Hexadiene"
conformer		display	C1-C2-C3-C4 dihedral	symmetry?	point group	Energy (in a.u.)	Relative Energy
conformer		display	C1-C2-C3-C4 dihedral	symmetry?	point group	Energy (in a.u.)	in a.u.	in kcal/mol
Anti	Anti 1^[7]		180	Yes	C₂	-231.6926	0.0000	0.00
	Anti 2^[8]			Yes	C_i	-231.6925	0.0001	0.06
	Anti 3^[9]			Yes	C_2h	-231.6890	0.0036	2.25
	Anti 4^[10]			Yes	C₁	-231.6909	0.0017	1.06
Gauche	Gauche 1^[11]		60	Yes	C₂	-231.6877	0.0049	3.07
	Gauche 2^[12]			Yes	C₂	-231.6916	0.0010	0.62
	Gauche 3^[13]			Yes	C₁	-231.6926	0.0000	0.00
	Gauche 4^[14]			Yes	C₂	-231.6915	0.0011	0.69
	Gauche 5^[15]			Yes	C₁	-231.6896	0.0030	1.88
	Gauche 6^[16]			Yes	C₁	-231.6891	0.0035	2.19

The energies are and will be cited to 4 decimal points, however, it should be noted that the energy values obtained from such calculations have an error value of 0.003 hartrees, CITE PATRICIA HUNT which corresponds to ~2 kcal/mol, so the absolute energies can not be used. Rather, comparisons will be drawn to the relative energies of different conformers.

The optimisations were carried out using HF/6-21G level of theory, which is only reliable to a certain limit, hence it was used only to get an overall minimisation of the geometries. It also gives enough information to get an overall idea of the relative stabilities, and this parameter will be analysed.

Before analysis, it is important to say that theoretically, it is possible to obtain a number of different conformations starting from just one, via the rotation of different C-C bonds. The fact that the assumption that these structures can exist without interconverting can be made, it effectively describes a situation where the structures presented are atropisomers, displaying a high rotational energy barrier about a single C-C bond. This hypothesis will be used later on, when explaining why the initial boat QST2 fails without including any dihedral modifications.

The HF/6-21G optimisation gives 3 low energy scenarios, the three being Anti1(C2), Anti2(Ci) and Gauche3(C1). The stability of the Anti2/Ci conformer is intuitive as it gives the C1-C2-C3-C4 dihedral as 180 and the two alkene groups as far away from each other as possible. This is the least stericaly hindered conformer. However, the further stability of the Anti1(C2) gives the possiblity of a through-space interaction between the two alkenes. This interaction is evidently dominant in affecting the stability, and is reasonable as the C=C bond is seen as a good donor in terms of second order stabilisation effects. The aforementioned hindrance is again dominant in giving the Gauche3 as the stable conformer, however given the through-space alkene interaction, the Gauche2 conformer should also be seen as a possible stable structure, despite its relatively high energy.

Using a higher level theory and 'Frequency Analysis'

A higher level optimisation was run on the Anti2(Ci) conformer using the DFT-B3LYP/6-31G(d) theory.^[17] This gives an important feature about the previous optimisation, as the DFT calculation did not change the previously HF-optimised structure, but gave a significantly different energy value. This can be seen in the table on the right.

Table 1.2 "Comparing the optimised Ci conformer for HF/6-21G and B3LYP/6-31g(d) theories"

Opt. Method

Anti2 / C_i conformer

display geometry

energy (in a.u.)

energy difference

in a.u.

in kcal/mol

HF/3-21G

HF/Ci

-231.6925

2.9192

1831.7

B3LYP/6-31G(d)

DFT/Ci

-234.6117

It it seen that the higher level optimised structure exhibits similar geometry with a more stable energy value by ~3 hartrees, which corresponds to a large energy(in kcal/mol) difference. To confirm the optimisation, the convergence criteria are displayed below;

Item               Value     Threshold  Converged?
 Maximum Force            0.000017     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000168     0.001800     YES
 RMS     Displacement     0.000076     0.001200     YES
 Predicted change in Energy=-1.655799D-08
 Optimization completed.
    -- Stationary point found.

ci_optimise_DFT
File Name = log_54856
File Type = .log
Calculation Type = FOPT
Calculation Method = RB3LYP
Basis Set = 6-31G(d)
Charge = 0
Spin = Singlet
E(RB3LYP) = -234.61170587 a.u.
RMS Gradient Norm = 0.00001383 a.u.
Imaginary Freq =
Dipole Moment = 0.0000 Debye
Point Group = CI
Job cpu time:  0 days  0 hours  2 minutes 23.4 seconds.

A frequency analysis was run on the DFT optimised Anti2(Ci) structure.^[18] The summary file of the frequency-structure was checked for energy values to confirm the calculation. The summary file did not give a different energy than the DFT-optimised structure, hence confirming the results. The low frequencies from the .log(.out) file are given below;

Low frequencies ---  -28.0346   -5.5853    0.0007    0.0008    0.0012    7.2328
 Low frequencies ---   74.9229   80.2304  119.9522

The low frequencies represent the motion of the Center of Mass of the molecule, and are essentially forbidden in terms of frequency analysis given that they imply a translation rather than a vibration. They are not as close to zero as they should be, but better zero-frequencies could not be otbained. However, the normal modes from the frequency analysis do not give any negative frequencies, indicating that a minimum is indeed obtained. The lowest two vibrations and the rest of the major ones are given below. The motions of the vibrations can be displayed.


#	bond/description	frequency (in cm^-1)	intensity	display
Vibration 1*	Symmetric bending of the two (C=C-C-) counterparts. Positive force constant implies the stability of the Newman conformation.	74	0.03	vibration1
Vibration 2*	Symmetric rotation/bending of the central C2-C3 carbons. Positive force constant implies the stability of the C1-C2-C3-C4 dihedral angle(180).	80	0.10	vibration2
Vibration 3	Rotation of terminal carbons about the C=C bonds resulting in overall motion of the molecule.	669	19.91	vibration3
Vibration 4	Umbrella deformation of the terminal carbons. The motion is inherently symmetric, however the residual strain gives an asymmetric motion as the magnitude of displacement is larger for the free hydrogens.	940	64.41	vibration4
Vibration 5	Intrinsic C=C stretch. Slightly higher frequency (free C=C around ~1630) due to residual strain caused by the rest of the molecule in -HC=H2.	1734	18.10	vibration5
Vibration 6	Asymmetric C-H stretch of the C1 and C4 carbons.	3136	56.02	vibration6
Vibration 7	Asymmetric C-H stretch of the terminal carbons.	3234	45.47	vibration7

The prominent peaks have been shown. The >3000 region overall corresponds to the C-H stretches of the different carbons. The two major peaks were given in the table and description of the motions of the vibrations have been made for the vibrations displayed.

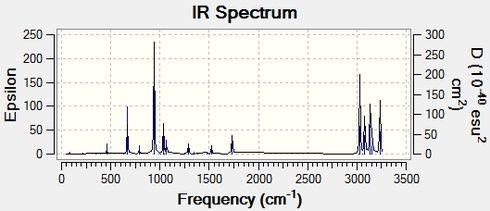
All vibrations are positive. This essentially means that the molecule is at a minimum on its potential energy surface and any distortions from this optimised structure will encounter an increase in overall energy, and hence a positive force constant (d²V/dx²=(+)). The thermochemistry information was obtained from the .log file. Since no certain temperature value was obtained at the beginning of the calculations, these values correspond to room temperature, 298.15 K.

at 298.15 K;

Sum of electronic and zero-point Energies=           -234.469242
Sum of electronic and thermal Energies=              -234.461887
Sum of electronic and thermal Enthalpies=            -234.460943
Sum of electronic and thermal Free Energies=         -234.500831


Blank line 0.0001 1.0 12.0 1.0 1.0 12.0 1.0 12.0 1.0 1.0 12.0 1.0 1.0 12.0 12.0 1.0 1.0 1.0 Bank line

The .log that was used to run the frequency analysis was edited, and 0K.1.0atm values were specified for the temperature and pressure parameters. The edited input file is given on the right. The first and the second terms correspond to temperature (in Kelvin) and pressure (in atm) respectively.

Before analysing the thermochemistry section, the paremeters will be defined.

Sum of electronic and zero-point Energies; (E = Eelec + ZPE); gives the said energies at 0K. This parameter is expected not to change with a temperature range of 0-295.K, as the electronic functions require a higher energy than room temperature.
Sum of electronic and thermal Energies; (E = E + Evib + Erot + Etrans); gives a complementary value to the first parameter. The values are calculated for 298.15K and 1 atm. Parameters are for the overall partition functions except the electronic one, namely rotational, vibrational and translational.
Sum of electronic and thermal Enthalpies; (H = E + RT); gives the enthalpy with respect to thermal degrees of freedom, RT.
Sum of electronic and thermal Free Energies: (G = H - TS); gives the Gibbs Free Energy, calculated from the enthalpy and entropy values.

Table 1.3 "Thermodynamic data obtained from frequency analysis at different temperature values"
T(K)	thermochemistry
T(K)	(1) Sum of electronic and zero-point Energies	(2) Sum of electronic and thermal Energies	(3) Sum of electronic and thermal Enthalpies	(4) Sum of electronic and thermal Free Energies
298.15	-234.469242	-234.461887	-234.460943	-234.500831
0*	-234.468805	-234.468805	-234.468805	-234.468805

T=0.0001 K

All the parameters are equal at 0K, which is expected as at 0K all of the parameters but the first will be equal to 0. Hence all of the parameters give (1) E = Eelec + ZPE, which is the sum of electronic and zero-point energies. However, it is seen that even parameter (1) is also dependent on temperature as it changes slightly from -234.4649 to -234.4688. Although, taking the correctional values into account, a difference of only ~0.001 a.u. is not significant. Hence, this is intuitive. It it also seen that the biggest difference is given in the free energy. This is again intuitive, as the entropic contribution is highly dependent on temperature.

Discussion

The conformational analysis of anti periplanar and gauche structures depend on a number of factors. Such factors may include both mechanical and electronic features, however in explaining the stability of the Gauche2 isomer, the stereoelectronic factors appear to be dominant. The following excerpt has been taken from Henry Rzepa's Year2 Conformational Analysis course.

"Conformational processes are dynamic and the thermodynamic equilibrium population of conformers about the C-C bonds is determined by:
       maximising σC-H/σ*C-H and/or σC-C/σ*C-C conjugation
       minimising σC-H/σC-H and/or σC-C/σC-C bond electron repulsion (Pauli repulsion)
       optimising van der Waals (dispersion) interactions between non-bonded atom pairs"

Of the 3 features described above, the first two were found to favour the app conformations, given the convenient overlap of anti-bonding C-H orbitals and the corresponding opposite C-H bonding orbitals. Effect three, however, favours the gauche conformer, as this feature relies on the through space overlap of the van der waahl radii of the H-H bonds. This overlap can be seen to be present in the Gauche conformers being studied, but instead of H--H interaction, the C=C bonds are that are close to each other would interact. The Newman projection of the Gauche2 conformer is given on the right, along with the HOMO of the conformer obtained at DFT RB3LYP/6-13G(d) level theory.

The HOMO of the Gauche2 conformer effectively shows evident orbital overlap of the two bonding alkene pi orbitals. However, it is intuitive that this effect would be observed for all the Gauche conformers, and not necessarily Gauche2, but it can be argued that this effect is at a maximum in this conformer since the two alkenes are as close to to each other as possible only in this conformer.^[19]

Chair & Boat Transition State Structures

The Allyl Fragment

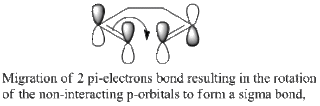
A mechanism relating the nature of the Cope rearrangement to two separate allyl fragments is given. Following this, the starting point to investigating the TS# structure can indeed be the optimisation of such a fragment and relating it to a boat and chair conformer. This feature is studied.

A single allyl fragment was drawn and optimised using HF/3-21G level of theory. The summary file is given below. Moreover, predictions were made relating the initial conformers to the chair and boat transition states. This is also shown in the diagram.

File Name = ALLYL_OPTIMISATION
File Type = .log
Calculation Type = FOPT
Calculation Method = UHF
Basis Set = 3-21G
Charge = 0
Spin = Doublet
E(UHF) = -115.82304010 a.u.
RMS Gradient Norm = 0.00002945 a.u.
Imaginary Freq =
Dipole Moment = 0.0292 Debye
Point Group = CS
Job cpu time:  0 days  0 hours  0 minutes 23.0 seconds.

It was mentioned earlier that despite the relative instability of the Gauche2 conformer compared to Gauche3 and Anti2, the through space interaction of the alkenes make it a viable candidate for a transition state structure. This is further confirmed when it was seen that its geometry is very close to a 6C-chair structure, shown on the diagram. This feature is further investigated.

Optimisation of Chair TS

HF/3-21G Level Optimisation to TS(Berny)

The very first optimisation for the chair transition state structure is the TS(Berny) method. The TS(Berny) parameter is essentially the same algorithm that is used to obtain minima in an optimisation, however with TS calculations it is used to obtain the maxima. The second parameter is the force constant. Force constants were calculated once at the beginning of the optimisation, which basically creates a Hessian force constant matrix only for the initial molecule and then imposes its predictions of each force constant with respect to the changes in the geometry of the initial molecule. Hence, this method is reliable when the transition state is close in geometry to the reactant, but might fail at longer ranges when the geometry is significantly different for the TS# state than the reactant.

An opt+freq was run using this criteria, and a single negative frequency value was obtained corresponding to the Cope rearrangement. This sort of vibrations are called imaginary frequencies, purely on the basis that the frequency of a harmonic motion includes the square root of 'k', or the force constant. Given a negative force constant, this would effectively give an imaginary number, as the frequency. The results are displayed later on along with the results obtained from the Redundant Coordinate Editor calculation. The second method is explained below.

Freezing Coordinates

Redundant Coordinate Editor breaks down the initial TS(Berny) optimisation into two steps, and these steps are explained. Again for this type of optimisation, some prior knowledge of the transition state is required in order to impose the Freeze Coordinate concept on the right bonds.

The first step is freezing the distances between the terminal carbons of each allyl fragment to 2.2A. The distance value is not arbitrary and was given in the script. Once the relative positions of these carbons are fixed, the rest of the molecule is then optimised to a normal minimum [TS(minimum)], and not a transition state. This effectively relaxes the rest of the molecule. Hence, this method can be seen as first minimising the parts of the molecule that don't play an important role in the transition state, then minimising the essential feature to a transition state energy.

The second part proceeds just as explained, which is to optimise the priorly frozen terminal carbons to a transition state via varying their distances. This second part makes use of TS(Berny) method and calculates force constants only once.

An opt+freq was run for this method as well as the first one, and the results are given below.

Comparing the straight-forward TS(Berny) optimisation to the Redundant Coordinates optimisation"
#		TS(Berny)^[20]	Modredundant^[21]^[22]	Display
#
Cope vibration	Frequency	-817	-818	copevibration
Cope vibration	Intensity	5.86	5.93	copevibration

It can be seen that both methods give similar results, with negligible differences. The negative frequency obtained corresponds to the Cope rearrangement, and gives the slope of the single-downward trajectory from the TS# state on the potential energy surface which leads to the global-minima structure that is the product. The motion of this vibration is identical in both methods, and is displayed on the table.

Optimisation of Boat TS: QST2 Method

Given that the transition state for the Cope rearrangement goes via a loose aromatic chair structure, the outcome of such a reaction can be predicted. It is evident that the reactant and product are similar, with the only difference being their connectivity/linkages. This gives a reaction that it highly compatible to QST2 calculations, and hence such a calculation was carried out.

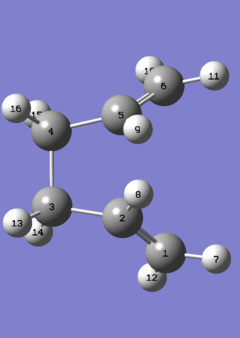
The QST2 method is useful when the reactant and products are known to exhibit no significant differences in geometry, and from this point on, the TS# structure can be predicted. However, it is crucial to make sure that the connectivity and the linkages are given as exact, and fully-defined. This is seen in the diagram given below, which shows the reactant and the product, and the varying atom lists corresponding to the Cope rearrangement.


reacttant	product

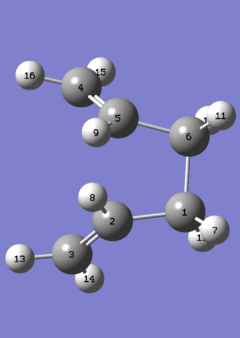It is important to note that the set-up given above for the QST2 calculation displays the dihedral-modified structures, after the initial attempt had failed. The failed run involved only the linear Ci conformers, which led to the wrong transition state. The failed TS# geometry can be viewed . The reason for this is that the QST2 method, as described above, requires most of the geometry modifications to be done prior to the calculation, meaning that Gaussian does not recognize the possibility of a rotation about the C2-C3 bond. This may be due to a number of reasons, however a reasonable one is given as the possible atropisomer nature of the bonds, explained in the very first discussion of the conformers. Hence, the dihedral modifications were done on the reactant and product, and the QST2 calculation was carried out. An opt+freq calculation gave the results tabulated below;

"Frequency analysis obtained from QST2 calculation"
#		QST2	display
#
Cope vibration	frequency	-840	image
Cope vibration	intensity	1.61	image

The negative vibration is similar to that of the chair TS#. However it is seen that the magnitude of the vibration implies a more steep downward trajectory, which can reasonably be associated with a higher energy TS# maxima on the potential energy surface. This effectively means that the boat structure can be seen as the more unstable TS#. This is confirmed via higher level theory optimisations, namely DFT B3LYP/6-31G(d). The results of these DFT optimisations are given later on.

Moreover, the two TS# states can be compared. Using HF/6-21G level theory, it it seen that the terminal carbons are closer in the chair TS# compared to the boat TS#, as the terminal C-C bond distance is given as 2.02 A and 2.14 A for chair and boat respectively. This might further confirm that the chair TS# is the more stable one, as the terminal C-C interaction is greater due to their proximity.

IRC: Intrinsic Reaction Coordinate

The definition of an intrinsic reaction coordinate can essentially be given as following the downward trajectory (given by the negative force constant) from the TS# state to the product minimum. This is useful since once the TS# structure has been obtained, it is possible to predict the products, which might not always be intuitive. Furthermore, in this case, predictions can be made regarding the possible outcome of the Cope rearrangement, however knowing for sure as to which conformer will be afforded is difficult. The boat calculations involved priorly defining the reactant and product, which was the Anti2(Ci) conformer, hence it is unnecessary to run an IRC on the boat TS# as one would obtain the product given in the atom list diagram. However, the chair TS# was obtained via different methods, none of which involved the product. Hence, an IRC was run on the chair TS#. This is discussed below.

The parameters for initial IRC run were set to 50 steps and calculate force constants 'once'. This did not give a fully optimised product, as the product had some but not definitive similarities to the initial 10 conformers. This was also seen in the RMS gradient norm, as the gradient for the last point was not close to 0 enough. Hence, from this point on, 3 more IRC calculations were run using different parameters. These parameters are discussed in the table below.

It should be noted that the initial 'failed' IRC is not given, however the IRC in the table using 100 steps is essentially identical to the initial one as both take 26 iterations and more steps don't make a difference.

"3 methods following the initial IRC"
#	chair
IRC parameter	minimise from last step^[23]	larger n of points (100)^[24]	force constant; always^[25]
display optimised geometry
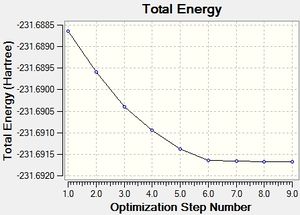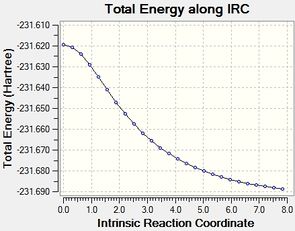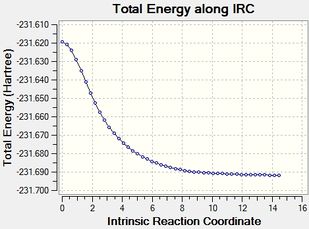IRC Path/Optimisation Plot	min	150steps	force
# of iterations	26(+9)	26	47
energy	-231.6916 (C₂)	-231.6886 (C₂)	-231.6916 (C₂)

The '100steps' does not give a different results compared to the initial IRC. Hence only the the first and third runs will be discussed. The first method in the table involves a normal optimisation from the geometry of the final point of the IRC. Hence, the initial 26 iteratin IRC along with an extra 9 iteration optimisation. The optimisation plot is given in the table. This method gives an optimised product, which can be associated with the Gauche2(C2) conformer.

Moreover, the energies match exactly, which indicates that this method is reliable. However, it should be noted that in order to rely on this method, the product must be close in geometry to the final structure in the IRC. As this is the case in this study, the method is successful, as well as simple.

The third method, which involves recalculating the Hessian for each step, is the most reliable one in terms of accuracy, as one can be sure that at each step, the optimisation will follow the downward trajectory with the greatest negative force constant. However, this takes a long time, hence it is not efficient. However, it gives a matching answer, both to the Gauche2 conformer and the first optimisation method. The IRC animation following the force constant run is given on the right.

B3LYP/6-31G(d) Optimisation: Calculating Activation Energies and Thermochemistry

Upon determining the correct transition states, a higher level DFT RB3LYP/6-31G(d) optimisation was run on both the structures. From the two optimised chair ts# structures, the TS(Berny) output was chosen and for boat, the only QST2 output was chosen.

The differences and advantages of using a higher level theory after a Hartree-Fock optimisation were discussed in a previous section. However, both the optimisation results are given in the table below for the chair and boat structures for further discussion.


TS#		chair		boat
Calculation Method/Basis Set		HF/3-21G	B3LYP/6-31G(d)^[26]	HF/3-21G	RB3LYP/6-31G(d)^[27]
E(in a.u.)	(RHF)	-231.6193	-	-231.6028	-
E(in a.u.)	(RB3LYP)	-	-234.5569	-	-234.5430
RMS Gradient Norm		0.00002366	0.00001243	0.00004598	0.00000404
Point Group		C1	C1	C2V	C2V
Display geometry
Convergence (for B3LYP optimisation)		Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000109 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-4.840135D-09 Optimization completed. -- Stationary point found.		Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000145 0.001800 YES RMS Displacement 0.000051 0.001200 YES Predicted change in Energy=-2.621937D-09 Optimization completed. -- Stationary point found.

At this point, it is important to remind oneself that the initial conclusion was that the two methods significantly differ only in energy, and not necessarily geometry. However, it is shown in the jmol files that a higher level theory does affects certain features, and these features only further prove an aforementioned hypothesis. This is discussed.

It was discussed that the chair ts# is more likely to be the stable one, and the boat relatively higher in energy. The differences between the DFT and HF optimisations give opposite directions for the two conformers, with the terminal C-C bonds shortening in the chair ts#, and vice versa in the boat ts# with higher level theory. The difference between the HF-optimised terminal C-C bond lengths lead to the initial prediction of the relative stability of the chair ts#, and given that a DFT optimisation only broadens this difference, it can be said that this prediction is pseudo-confirmed.

Moreover, the E(B3LYP) values can be compared. It it seen that the chair ts# is stable in energy by a value of 0.0139 a.u., which corresponds to 8.72 kcal/mol. This is a significant difference that would most likely affect the favoured reaction trajectory in the direction of the chair ts#.

Following this definitive conclusion reached from the results obtained, one could effectively calculate the activation energy required in order to force the reactant (conformers) over the saddle point in the potential energy surface and afford the Cope rearrangement. The association of the chair ts# to the Gauche2/C2 conformer and the boat ts# to the Anti2Ci conformer was previously discussed. Following this, the said conformers were optimised with the higher DFT B3LYP/6-31G(d) level theory with their energies given below. Below, is also given the activation energies calculated from subtracting the reactant energies from the corresponding transition state energies at DFT level calculation.


#	energy (in a.u.) at 298.15 K		activation energy
	energy (in a.u.) at 298.15 K		T 298.15 K			T 0 K
	Reactant Conformer/Energy-E(RB3LYP)		TS# Energy	in a.u.	in kcal/mol	TS# Energy	in a.u.	in kcal/mol
chair	Gauche2/C2	-234.6106	-234.5569	0.0537	33.69	-	-	-
boat	Anti2/Ci	-234.6117	-234.5430	0.0687	43.10	-	-	-

1 Hartree = 627.5 kcal/mol

The results agree with literature for the 298.15 K. Moreover, the activation energy can be calculated for 0K. However, this is done via comparing the sum of electronic and zero-point energies of the products and reactants. The thermochemistry data obtained for both ts# structures is given below, and the 0K calculation follows.


#	Thermochemistry
	298.15 K				0 K
	Sum of electronic and zero-point Energies	Sum of electronic and thermal Energies	Sum of electronic and thermal Enthalpies	Sum of electronic and thermal Free Energies	Sum of electronic and zero-point Energies	Sum of electronic and thermal Energies	Sum of electronic and thermal Enthalpies	Sum of electronic and thermal Free Energies
chair	-234.414929	-234.409008	-234.408064	-234.443814	-234.414485	-234.414485	-234.414485	-234.414485
boat	-234.402342	-234.396008	-234.395063	-234.431097	-234.401903	-234.401903	-234.401903	-234.401903

The intrinsics of the thermochemistry data were previously analysed and discussed hence no further analysis will be given here. However it is worth noting that the zero-point energies given in the 0K calculations give a very similar difference to that obtained from the optimisation energies, hence such an interpolation is viable. So, these values will be used to calculate the activation energies of the ts# structures at 0K.

The thermochemistry data for the Ci conformer was given in the first section as -234.468805 a.u.. The Gauche2 conformer was then run with opt+freq at higher level theory and at 0K^[28], and its zero-point energy was found to be -234.467826.


#	at 0 K (in a.u.)^[29]		energy difference
#	reactant energies	ts# energies	in a.u.	in kcal/mol
chair ts#	Gauche2, -234.467826	-234.414485	0.0534	33.50
boat ts#	Ci, -234.468805	-234.401903	0.0669	41.97

This gives enough data for an activation energy calculation. Hence for the chair ts# the activation, the activation energy at 0K is the difference between E(chair)=-234.414485 and E(Gauche2)=-234.467826, and for boat ts# it is the difference between E(boat)=-234.401903 and E(Anti2)=-234.468805. The results are tabulated on the right, and the thermochemistry data for Gauche2 given below for reference.

Thermochemistry data for Gauche2(C2) conformer for reference;

Sum of electronic and zero-point Energies=           -234.467826
 Sum of electronic and thermal Energies=              -234.467826
 Sum of electronic and thermal Enthalpies=            -234.467826
 Sum of electronic and thermal Free Energies=         -234.467826

The Diels-Alder Reaction: Comparing Transition States

Outline/Overview

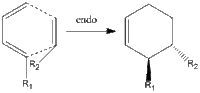
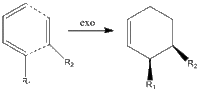
The Diels-Alder reaction, first documented in 1928, is long known to have regioselective properties upon the inclusion of R-groups to vary the nature of the dienophile/diene. Moreover, it is known that the reaction proceeds via two pathways, namely the endo and exo approches. These are shown in the simplest terms on the right.

The study focuses on semi-empirical calculations as well as higher level theory to afford the molecular orbitals of the aforementioned two transition states, which essentially forms the basis of a reasonable conclusion. The exo approach is known to give the thermodyamic product, however it is known that the endo ts# lies lower in energy than the exo ts#. This is studied with respect to the molecular orbitals and the second order orbital interactions within the ts# structure.

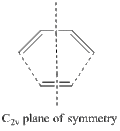
Cis-butadiene: A Precursor to Regioselective [4s+2s] Diels-Alder

The symmetry of cis-butadiene was found to be C2v. The axis and plane of symmetry is shown on the diagram on the right. It is only intuitive to expect the same symmetry from the molecular orbitals, and this is indeed what one gets. MO's were obtained using semi-empirical AM1 theory and the molecule optimised prior to MO analysis. The HOMO and LUMO levels are given below, both showning symmetrical features about the C2 axis and sigma v-plane of symmetry.


homo	lumo

The orbitals have been displayed to show C2v symmetry, with the HOMO displaying anti-symmetric nature and the lUMO showing symmetric nature. The energy of the molecule was calculated from the optimisation ran prior to MO analysis. This is given below for future reference.

Total Energy = 0.04879718 a.u.

Furthermore, it is known that the HOMO and LUMO levels of ethylene are symmetric and anti-symmetric respectively, hence in the context of a Diels-Alder reaction between cis-butadiene and ethylene, the only allowed interactions are between the HOMO/LUMO levels.

Reaction between Ethylene/Cis-butadiene: Transition State Analysis

diels ts berny

The diagram showing the plane of symmetry discussed in the previous section is given on the right.

Similar optimisation and MO calculations have been run on the TS# state, which has been calculated using TS(Berny) with the force constant set to 'calculate once'. Despite the simplicity of the method, an acceptable ts# state was obtained. The ts# state is displayed as a jmol on the right.

The summary file of the optimisation is given below as well as the HOMO/LUMO of the ts#;

File Name = diels_ts#_berny
File Type = .chk
Calculation Type = FTS
Calculation Method = RAM1
Basis Set = ZDO
Charge = 0
Spin = Singlet
Total Energy = 0.11165466 a.u.
RMS Gradient Norm = 0.00000956 a.u.
Imaginary Freq =
Dipole Moment = 0.5607 Debye
Point Group = C2v

Total Energy = 0.11165466 a.u.
RMS Gradient Norm = 0.00000956 a.u.

The HOMO/LUMO of the ts# state of the Diels-Alder reaction ethylene and cis-butadiene are given. It is evident that the initial C2v symmetry of the reactants has been retained, as the HOMO is still anti-symetric and the LUMO symmetric. Moreover, it is worth mentioning that an energy value of 0.1116 a.u. for the TS(Berny) optimisation has been obtained for the TS# state structure.

The nodal properties of the molecular orbitals can be viewed in the display. It it evident that the HOMO is a result of mixing between the HOMO of cis-butadiene and the LUMO of ethylene, as both are anti-symmetric orbitals and their mixing would also afford an anti-symmetric MO. This is seen. Such mixing describes a scenario where the cis-butadiene is the nucleophile, and the ethylene the electrophile. This is indeed the underlying theory behind the diene-dienophile relationship in a 4+2 Diels-Alder reaction. Vice versa for the LUMO is observed, as the LUMO of the ts# exhibits symmetric nature, as a results of the mixing of two symmetric mo's, the LUMO of cis-butadiene and HOMO of ethylene.

The resulting ts# state is a pseudo-chair conformation with the terminal C-C distances being equal to 2.2 A. Moreover, it it seen that the C=C bond distance in the ethylene molecule is longer in the ts# structure compared to free ehtlyene, which again is indicative of the occupation of the LUMO, hence decreasing the bond order. The product gives the intuitive cyclohexene.

Reaction between Maleic Anhydride/Cyclodiene: A Regioselective Diels-Alder

Outline

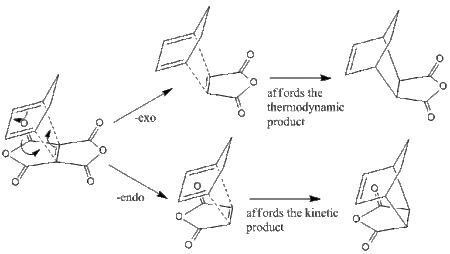
The inclusion of certain R groups on the dienophile in the context of a Diels-Alder reaction gives rise to the possible aspects regarding regioselectivity. Given maleic anhydride as the dienophile, the presence of secondary orbital interactions and perturbation become dominant, and this would in theory effectively lower down the energy of one of the transition state structures, namely endo or exo.

It is known that the said NBO stabilisation results in a more stabilised endo ts# structure, and this is eplained as the -(C=O)-O-(C=O)- fragment would be aligned below the mo's of =C-C= fragment of the diene which would mean a better overlap of the otherwise non-interacting MO's. This is studied.^[30]^[31]

Reactants

The reactants, namely cyclodiene and maleic anhydride, were optimised at the semi-empirical AM1 theory prior to any ts# calculations, and their energies given below.

cyclodiene;

E(RAM1) = 0.02795815 a.u.
RMS Gradient Norm = 0.00005245 a.u.

maleic;

E(RAM1) = -0.12182422 a.u.
RMS Gradient Norm = 0.00002022 a.u.

Since energy values are additive, the overall E(RAM1) is given as;

(-0.1218) + (0.0279) = -0.1497 a.u.

This value is used later on when the activation energies are calculated for the two ts# states.

Transition State Study: Comparing the endo/exo

The two ts# states were obtained using two different methods. The semi-empirical AM1 level of theory was used as the initial method, and following this, a QST2 was set up and optimised using DFT RB3LYP/6-31G(d) theory. Given below are the resutls from the TS(Berny) calculation at semi-empirical AM1 level theory where the force constant was calculated only once.

The two ts# structures aer given on the right as jmols. A compare and contrast discussion was made based on key features obtained from the structures. These features are given in the table below.

exo ts berny

Exo

endo ts berny

Endo

blabl
Parameter		exo	view	endo	view
Bond distance	C=C	1.41 A	-	1.41 A	-
	(C=O)-O-(C=O)-(-CH2-CH2-)	2.95 A	-	2.89	-
	(C--C)(TS# Bond)	2.17 A		2.16
Angle*	1* (C--C)-(C=O)-O-	99.60	-	100.01	-
Angle*	2* (-CH2-CH2-)-(C--C)	99.8		94.8

The important parameters included in the table have been shown in the jmols on the right

The initial measurement was the terminal C-C bond distances of the ts# structures. Prior to this, it was thought that this distance would differ for the two structures, however the difference was found to be insignificant, as both give roughly ~2.16 A. Moreover, some other key features that were initialy thought to differ also gave similar results. The dienophile C=C bonds can be seen to be identical for both ts# structures, however it is only intuitive that upon comparison with the reactant maleic anhydride, the difference would be significant. The C=C bond would evidently be shorter for the free maleic anhydride, as in the ts# structure this alkene is being attacked on the LUMO, its anti-bonding orbital. However, this donation from the HOMO of the cyclodiene into the LUMO of the C=C is the same for both ts# structures, hence resulting in identical bond lenghts. The varying feature would effectively be the position of the -(C=O)-O-(C=O)- fragment, as this is responsible for lowering the overall energy of the endo.

Two key features come to mind when analysing the position of the -(C=O)-O-(C=O)- fragment. The steric repulsion of the group with the -CH2-CH2- bridge in the cyclodiene structure, and the overall attraction between the said fragment and the =CH-CH= fragment of the diene. Hence, the angle between the bridge and the incipient C--C bond in the ts# structures were measured and found to be different, as shown in the jmols. Moreover, the through space distances between the opposite carbon groups to the maleic anhydride were measured and also shown in the jmols. It is evident that the exo suffers from steric repulsion between the maleic anhydride C=O fragments, whereas this repulsion is effectively an attraction in the endo structure, shown as a shorter through space distance in the endo compared to the exo. This is explained using MO analysis, given further below.

Upon optimising the two structures, frequency analysis was carried out to confirm that the ts# structures were correct. A single negative frequency vibration was obtained for both structures, and the motion of the vibration was animated and given below as the corresponding Diels-Alder vibration.


# Method(Semi-empirical/AM1)	exo			endo
# Method(Semi-empirical/AM1)	frequency	intensity	display	frequency	intensity	display
diels-alder vibration	-812	96.88	exo vibration	-806	71.57	endo vibration

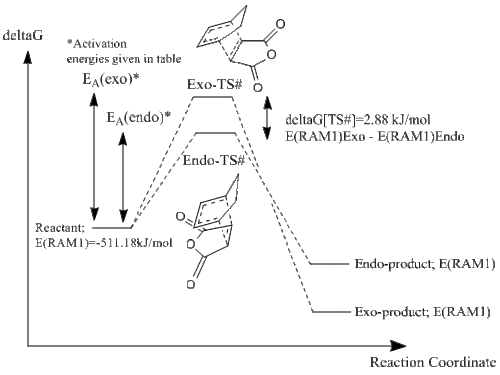
It is useful to interpret the given magnitudes of the vibrations with respect to the potential energy surfaces of the two states. The energies obtained from the semi-empirical RAM1 optimisations of the structures are given below. They effectively show a difference between the energies, with the endo ts# being more stable relative to the exo ts# by 2.88 kJ/mol.


#		E(RAM1)	Relative Energy, ~deltaG[TS#]	deltaG[TS#]
#		energy in a.u.		energy in kJ/mol
endo	Total Energy	-0.05150478	0.0011	2.88
endo	RMS Gradient Norm	0.00000859
exo	Total Energy	-0.05041984
exo	RMS Gradient Norm	0.00000442

This is as expected. Hence, on a potential energy surface, this puts the exo at a higher maxima, with respect to the endo. This essentially means that given the thermodynamic nature of the exo, upon proceeding in the reaction coordiante the IRC will give a more step downward trajectory, resulting in a larger second derivative of the potential energy. This is confirmed, as the vibrational mode of the Diels-Alder motion is larger for the exo compared to the endo, by ~6 cm^-1.

The data obtained from several calculations are displayed in the free energy diagram given below.

1 Hartrees = 2625.5 kJ/mol

The energy diagram below shows the computational data obtained in this study, which so far do not reach beyond the ts# structures. Hence, the relative positions of the product with respect to each other is only a prediction, based on the knowledge that the exo approach gives the thermodyamic product, and the endo approach gives the kinetic. This is essentially confirmed via the ts# calculations, however the energy of the products also have to be calculated for a definitive conclusion. These energy values have been obtained later along using the QST2 method.

The extent of this second order orbital stabilisation is studied using MO analysis. The MO' were obtained for both the endo and exo ts# structures, and starting from the HOMO level, 4 orbitals were selected, with more focus put on the LUMO+2 level. The orbitals are given below;


#	HOMO	LUMO	LUMO+1	LUMO+2*
exo	homo	lumo	lumo+1	lumo+2
endo	homo	lumo	lumo+1	lumo+2

It it seen that at the LUMO+2 level, further mixing occurs between the oxygen-fragment of the maleic anhydride and the =CH-CH=. This explains the relative stability of the endo and confirms the prediction made earlier. Moreover, NBO analysis was run on the ts# state of the endo and the extent of this stabilisation was investigated. However the corresponding stabilisation energy could not be found. It should be noted that only the values that exceeded a stabilisation energy of 10 kj/mol were studied, hence this could effectively mean that the stabilisation at hand is not a significant one, as it is more likely a weak one (<10kJ/mol). NBO analysis was run using DFT level RB3LYP/6-31G(d) theory.

4. BD (   1) C   1 - C  12        /194. BD*(   1) C   2 - C  15           11.34    0.29    0.052
   4. BD (   1) C   1 - C  12        /198. BD*(   2) C   6 - O   7           18.62    0.30    0.070
   4. BD (   1) C   1 - C  12        /202. BD*(   2) C  10 - C  11           17.73    0.32    0.068
   7. BD (   1) C   2 - C  15        /191. BD*(   1) C   1 - C  12           11.33    0.29    0.052
   7. BD (   1) C   2 - C  15        /200. BD*(   2) C   8 - O   9           18.62    0.30    0.070
   7. BD (   1) C   2 - C  15        /202. BD*(   2) C  10 - C  11           17.73    0.32    0.068
  15. BD (   2) C  10 - C  11        /191. BD*(   1) C   1 - C  12           17.05    0.27    0.060
  15. BD (   2) C  10 - C  11        /194. BD*(   1) C   2 - C  15           17.05    0.27    0.060
  43. LP (   2) O   5                /198. BD*(   2) C   6 - O   7           36.56    0.32    0.098
  43. LP (   2) O   5                /200. BD*(   2) C   8 - O   9           36.56    0.32    0.098
  44. LP (   1) O   7                / 80. RY*(   1) C   6                   18.14    1.43    0.144
  45. LP (   2) O   7                /190. BD*(   1) C   1 - C   6           18.46    0.65    0.101
  45. LP (   2) O   7                /195. BD*(   1) O   5 - C   6           37.29    0.55    0.129
  46. LP (   1) O   9                /100. RY*(   1) C   8                   18.14    1.43    0.144
  47. LP (   2) O   9                /193. BD*(   1) C   2 - C   8           18.46    0.65    0.101
  47. LP (   2) O   9                /196. BD*(   1) O   5 - C   8           37.29    0.55    0.129
 191. BD*(   1) C   1 - C  12        /202. BD*(   2) C  10 - C  11           91.25    0.02    0.071
 194. BD*(   1) C   2 - C  15        /202. BD*(   2) C  10 - C  11           91.26    0.02    0.071

Most of the C-O stabilisations refer to an intra-molecular stabilisation within the maleic anhydride structure. Namely lone pair stabilisations of the neighbouring C-O anti-bonding orbitals. The last two interactions show the aromatic structure of the ts#, and hence this is the greatest stabilisation.

Given that the said second order electronic interaction is not the defining parameter of stabilisation, the relative stability of the endo ts# must be explained using a mechanics points of view, namely strain. The angle of approaches and the through space distances of the maleic anhydride fragment and the opposite C-C fragments have been measured and given before, which shows that the exo ts# is destabilised mostly because of the steric clashing between the hydrocarbon bridge and the CO-O-CO fragment. This steric hindrance would be present in the exo ts# as well, however the second order orbital effect prevents it and makes this a slightly (very slightly!) favourable interaction.

Method 2: QST2 and IRC Calculations

The ts# structures were further studied using QST2 as a second method with a higher DFT basis set theory for comparison.

The vibrational modes obtained effectively have identical motions, all associated with the Diels-Alder reaciton, hence only the magnitudes of the vibrations are given and will be compared.


#(Parameter)	TS(Berny)		QST2
Basis Set	Semi-empirical/RAM1		DFT-RB3LYP/6-31G(d)
Calculate Force Constants	Once
#(Conformer)	Frequency Analysis
#(Conformer)	Exo	Endo	Exo	Endo
Frequency (in cm^-1)	812	806	448	447
Intensity	96.88	71.57	5.50	1.43

The relative vibrations within different methods and basis sets show identical relationships, with the negative frequency having a greater magnitude for the exo ts# for both methods. This is discussed in the previous section. Furthermore, it is important to note that one can not possibly compare the results obtained via different basis sets, and this section only focuses on the comparison drawn within the basis sets.

It is worth mentioning that the initial QST2 calculation was run using the semi-empirical RAM1 theory, and this calculation afforded identical results with the initial TS(Berny) run. This was already seen and both method compared for the chair ts# optimisation, and as a result, the higher level DFT method was chosen for a different set of results as well as accuracy.

The ts# structures obtained from the QST2 calculations are given on the right. The two main features discussed earlier are given for both methods for compare and contrast.

It it seen that the difference between the endo and exo is not so significant in the QST2[DFT-RB3LYP/6-31G(d)] calculations, moreover the magnitude of the calculation evidently smaller compared to the semi-empirical RAM1. These magnitudes can only be compared via referring to the algorithms used in the calculation methods, but in depth analysis will not be given.

The results of the IRC calculations are given below.


#	QST2 IRC calc.
#	exo^[32]	endo^[33]
View optimised ts# structure^[34]^[35]
IRC Plot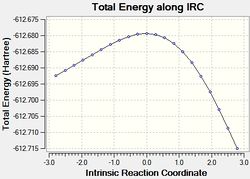
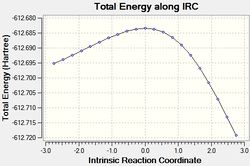RMSGradient Plot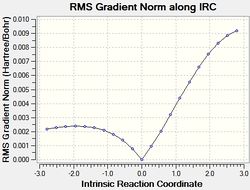
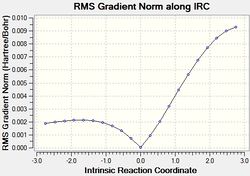Energy	-612.6925	-612.7192
View Motion of PES Trajectory

The IRC calculations gave the expected products, however it should be noted that the displayed energies associated with the kinetic and thermodynamic products are not intuitive. Furthermore, the energies show the exo approach to afford the less stable product. This is discussed.

MM2 calculations were run on the two products as well as MOPAC/PM6 on ChemBio3D. MM2 still gave the endo product to be the favourable one( ~35 kcal/mol for endo, ~36 kcal/mol for exo), however MOPAC/PM6 gave a heat of formation value of -100 kcal/mol for endo, and -108 kcal/mol for exo. This essentially means that the stabililty is an electronic effect, given that MOPAC differentiates between the products the right way, however in module 1 the MM2 calculation for the cyclopentadiene dimer showed the exo to be lower. Hence, it could effectively be that the endo/exo labelling might not apply to this situation.

Conclusion

2 systems were studied. The Cope rearrangement was shown to progress via an aromatic structure, and the two structures, boat and chair, were compared and contrasted to determine their relative stabilities. The chair conformation was found to be more stable for the transitions state, and this was further proven using higher level theory and basis sets.

The regioselective 4s+2s Diels-Alder reaction between cyclohexadiene and maleic anhydride was studied, and the endo/exo approaches to the ts# structure given in terms of their energies and relative stabilities. Moreover, a standard Diels-Alder between ethylene and cis-butadiene was investigated, with more focus put on the symmetrical aspect of the molecule and its molecular orbitals. The results obtained from the Diels-Alder study were not intuitive throughout, as the association of the thermodynamic and kinetic products to the exo and endo approaches proved difficult to assign. The endo indeed displayed more stability not just as a transition state, but also as the product of the concerted reaction. This was discussed in the relevenat section.

References

↑ 2nd Year Physical Labs, Experiment: "Molecular Reaction Dynamics"
↑ 3rd Year Computational Labs, Lab Script
↑ 'Density Functional Theory Isotopse Efefcts and Activation Energies for the Cope and Claisen Rearrangements'. Olaf Wiest, Kersey Black, K.N. Houk. J. Am. Chem. Soc., 1994, 116 (22), pp 10336–10337 DOI: 10.1021/ja00101a078
↑ 'Cope Rearrangement Revisited'. Roald Hoffmann, Wolf D. Stohrer. J. Am. Chem. Soc., 1971, 93 (25), pp 6941–6948.DOI: 10.1021/ja00754a042
↑ D. L. Boger, M. Patel. Proy. Heterwycl, Cheiw. 1989, /, 30-64.
↑ J. Sauer, R. Sustmann, Angrw. Chrm. Int. Ed. EnyI. 1980, 19, 779.
↑ http://hdl.handle.net/10042/to-12576
↑ http://hdl.handle.net/10042/to-12577
↑ http://hdl.handle.net/10042/to-12579
↑ http://hdl.handle.net/10042/to-12575
↑ http://hdl.handle.net/10042/to-12580
↑ http://hdl.handle.net/10042/to-12581
↑ http://hdl.handle.net/10042/to-12584
↑ http://hdl.handle.net/10042/to-12585
↑ http://hdl.handle.net/10042/to-12583
↑ http://hdl.handle.net/10042/to-12586
↑ http://hdl.handle.net/10042/to-12587
↑ http://hdl.handle.net/10042/to-12588
↑ 2nd Year Organic Course, 'Conformational Analysis'. Henry Rzepa.
↑ http://hdl.handle.net/10042/to-12589
↑ http://hdl.handle.net/10042/to-12590
↑ http://hdl.handle.net/10042/to-12591
↑ http://hdl.handle.net/10042/to-12594
↑ http://hdl.handle.net/10042/to-12592
↑ http://hdl.handle.net/10042/to-12593
↑ http://hdl.handle.net/10042/to-12596
↑ http://hdl.handle.net/10042/to-12597
↑ http://hdl.handle.net/10042/to-12602
↑ http://hdl.handle.net/10042/to-12601
↑ Synthesis in the hydroaromatic series, IV. Announcement: The rearrangement of malein acid anhydride on arylated diene, triene and fulvene, Diels, O.; Alder, K. Ber. 1929, 62, 2081 & 2087.
↑ Niobium Pentachloride Activation of Enone Derivatives: Diels–Alder and Conjugate Addition Products Mauricio Gomes Constantino, Valdemar Lacerda Júnior and Gil Valdo José da Silva Molecules 2002, 7, 456–465.
↑ http://hdl.handle.net/10042/to-12605
↑ http://hdl.handle.net/10042/to-12606
↑ http://hdl.handle.net/10042/to-12603
↑ http://hdl.handle.net/10042/to-12604

[1] 2nd Year Physical Labs, Experiment: "Molecular Reaction Dynamics"

[2] 3rd Year Computational Labs, Lab Script

[3] 'Density Functional Theory Isotopse Efefcts and Activation Energies for the Cope and Claisen Rearrangements'. Olaf Wiest, Kersey Black, K.N. Houk. J. Am. Chem. Soc., 1994, 116 (22), pp 10336–10337 DOI: 10.1021/ja00101a078

[4] 'Cope Rearrangement Revisited'. Roald Hoffmann, Wolf D. Stohrer. J. Am. Chem. Soc., 1971, 93 (25), pp 6941–6948.DOI: 10.1021/ja00754a042

[5] D. L. Boger, M. Patel. Proy. Heterwycl, Cheiw. 1989, /, 30-64.

[6] J. Sauer, R. Sustmann, Angrw. Chrm. Int. Ed. EnyI. 1980, 19, 779.

[7] ttp://hdl.handle.net/10042/to-12576

[8] ttp://hdl.handle.net/10042/to-12577

[9] ttp://hdl.handle.net/10042/to-12579

[10] ttp://hdl.handle.net/10042/to-12575

[11] ttp://hdl.handle.net/10042/to-12580

[12] ttp://hdl.handle.net/10042/to-12581

[13] ttp://hdl.handle.net/10042/to-12584

[14] ttp://hdl.handle.net/10042/to-12585

[15] ttp://hdl.handle.net/10042/to-12583

[16] ttp://hdl.handle.net/10042/to-12586

[17] ttp://hdl.handle.net/10042/to-12587

[18] ttp://hdl.handle.net/10042/to-12588

[19] 2nd Year Organic Course, 'Conformational Analysis'. Henry Rzepa.

[20] ttp://hdl.handle.net/10042/to-12589

[21] ttp://hdl.handle.net/10042/to-12590

[22] ttp://hdl.handle.net/10042/to-12591

[23] ttp://hdl.handle.net/10042/to-12594

[24] ttp://hdl.handle.net/10042/to-12592

[25] ttp://hdl.handle.net/10042/to-12593

[26] ttp://hdl.handle.net/10042/to-12596

[27] ttp://hdl.handle.net/10042/to-12597

[28] ttp://hdl.handle.net/10042/to-12602

[29] ttp://hdl.handle.net/10042/to-12601

[30] Synthesis in the hydroaromatic series, IV. Announcement: The rearrangement of malein acid anhydride on arylated diene, triene and fulvene, Diels, O.; Alder, K. Ber. 1929, 62, 2081 & 2087.

[31] Niobium Pentachloride Activation of Enone Derivatives: Diels–Alder and Conjugate Addition Products Mauricio Gomes Constantino, Valdemar Lacerda Júnior and Gil Valdo José da Silva Molecules 2002, 7, 456–465.

[32] ttp://hdl.handle.net/10042/to-12605

[33] ttp://hdl.handle.net/10042/to-12606

[34] ttp://hdl.handle.net/10042/to-12603

[35] ttp://hdl.handle.net/10042/to-12604

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]