Rep:Mod:jamie2
Transition States and Reactivity
Introduction
Through the examples of the Cope rearrangement and the Diels Alder cycloaddition the reactant, product and transition state structures on potential energy surfaces were investigated, analysed and characterised. GaussView and Gaussian was used to optimise geometries, frequency analyse molecules, run intrinsic reaction coordinate calculations and calculate activation energies.
Cope Rearrangement
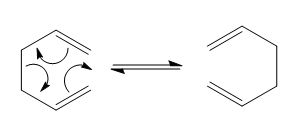
The cope rearrangement was first discovered in 1940 [1]. It is a [3,3]-sigmatropic rearrangement, a type of pericyclic reaction. This means that bonds are made and broken via a concerted cyclic transition state. Here we will be investigating the cope rearrangement of 1,5-hexadiene as shown below.
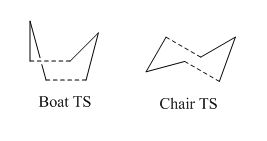
The mechanism can proceed via either a chair or boat transition state. These transition states are shown below, with the chair being the lower energy.
We will use computational methods to optimise the the geometries of the reactants, products and transitions states in order to study the reaction path and the changes in energy associated with the reaction.
Reactants and Products
'Anti' linkage Optimisation
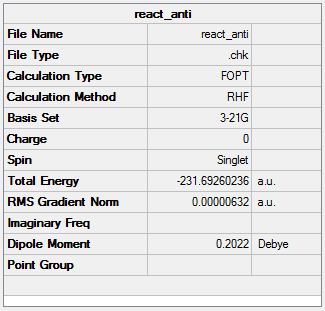
1,5-hexadiene was drawn with an 'anti' linkage for the central four atoms and was then optimised using the Hartree Fock method and the basis set 3-21G. The chk. file is shown here (File:React anti.chk). The optimised molecule is shown below along with its summary and item table (item table from .log file).
Item Value Threshold Converged?
Maximum Force 0.000020 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.001290 0.001800 YES
RMS Displacement 0.000388 0.001200 YES
Predicted change in Energy=-1.205949D-08
Optimization completed.
-- Stationary point found.
The item table above shows that the forces and displacements were optimised, hence the optimisation was successful and a stationary point was found.
The molecule was symmetrized to give C2 symmetry. The summary table above shows C1 but the molecule's higher symmetry was obtained when the molecule was symmetrized. The energy matches with the anti 1 conformer from appendix 1.
Gauche linkage optimisation
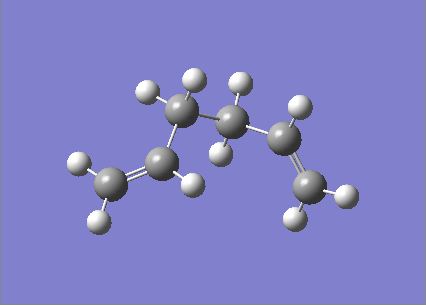
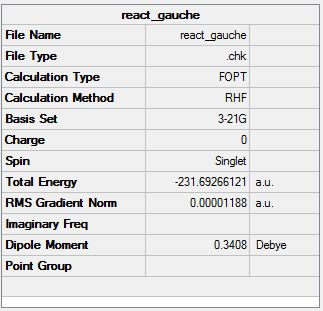
Another molecule of 1,5-hexadiene was drawn with a gauche conformation for the central 4 atoms. The molecule was optimised using the the Hartree Fock method and the basis set 3-21G. The .chk file is shown here (File:React gauche.chk). The optimised molecule is shown below along with its summary and item table (item table from .log file).
Item Value Threshold Converged?
Maximum Force 0.000034 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.001028 0.001800 YES
RMS Displacement 0.000316 0.001200 YES
Predicted change in Energy=-1.975016D-08
Optimization completed.
-- Stationary point found.
It can be seen from the item table that the forces and displacements converged and the molecule was optimised.
The molecule was symmetrized to give C1 symmetry.
The energy of this conformer with a gauche conformation has an energy of -231.69266121 a.u. . This energy matches with the gauche 3 conformer from appendix 1. This is lower in energy than the conformer with the anti conformation for the central 4 atoms, which has an energy of -231.69260236.
Conformer Investigation
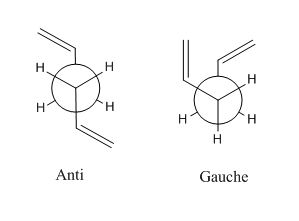
The energies have been found for two of the possible conformers of 1,5-hexadiene. There are an infinite number of conformers possible due to rotation around the C-C bonds. If the lowest energy conformer is to be found all of these need to be investigated. As shown above the lowest energy conformers lie where there is either a gauche or an anti linkage. The newmnan projections of these conformations are shown below.
All possible gauche and anti conformers will be drawn and optimised using the same HF/3-21G level of theory. A table of isomers is shown below. For the optimisations in this table the item and summary tables are not shown. Every isomer converged when the optimisation was performed.
| Conformer | Structure | Energy (a.u.) HF/3-21G | Energy (kcal/mol) | Relative Energy (kcal/mol) | Point Group | .chk File |
|---|---|---|---|---|---|---|
| Gauche 1 | 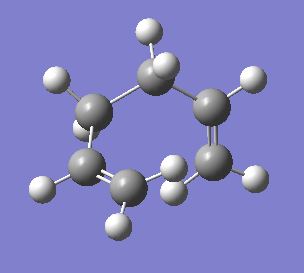 |
-231.68771617 | -145386.1271 | 3.10 | C2 | File:React gauche1.chk |
| Gauche 2 | 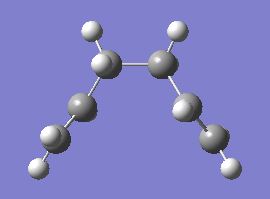 |
-231.69166702 | -145388.6063 | 0.62 | C2 | File:React gauche2.chk |
| Gauche 3 | 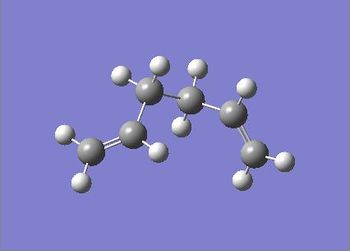 |
-231.69266122 | -145389.2301 | 0.00 | C1 | File:React gauche.chk |
| Gauche 4 | 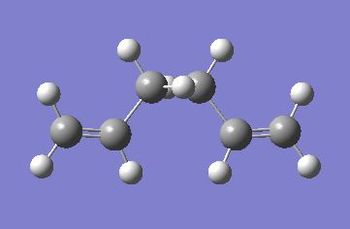 |
-231.69153033 | -145388.5035 | 0.73 | C2 | File:React gauche4.chk |
| Gauche 5 |  |
-231.68961574 | -145387.3191 | 1.91 | C1 | File:React gauche5.chk |
| Gauche 6 |  |
-231.68916016 | -145387.0332 | 2.20 | C1 | File:React gauche6.chk |
| Anti 1 |  |
-231.69260236 | -145389.1932 | 0.04 | C2 | File:React anti.chk |
| Anti 2 |  |
-231.69253528 | -145389.1511 | 0.08 | Ci | File:React anti2.chk |
| Anti 3 |  |
-231.68907066 | -145386.977 | 2.25 | C2h | File:React anti3.chk |
| Anti 4 |  |
-231.69097048 | -145388.1692 | 1.06 | C1 | File:React anti4.chk |
Optimisation with Higher Basis Set
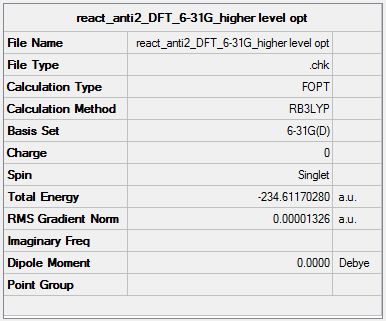
The chk. file from the optimisation of the Ci anti2 isomer was reopened and optimised using a higher level of theory. The method was changed from Hartree-Fock to DFT B3LYP and the basis set changed to 6-31G(d). The file is shown here (File:React anti2 DFT 6-31G higher level opt.chk). The optimised structure, summary table and item table are shown below (item table from .log file).
Item Value Threshold Converged?
Maximum Force 0.000015 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000219 0.001800 YES
RMS Displacement 0.000079 0.001200 YES
Predicted change in Energy=-1.588981D-08
Optimization completed.
-- Stationary point found.
It can be seen that the optimised geometries from the HF/3-21G and B3LYP/6-31G* levels of theory are very similar. The energies however are quite a bit different, -231.69253528 for HF/3-21G and -234.61170280 for B3LYP/6-31G*. B3LYP/6-31G* has a lower energy. Different basis sets use different approximations so this is why there is an energy mismatch.
Frequency Analysis
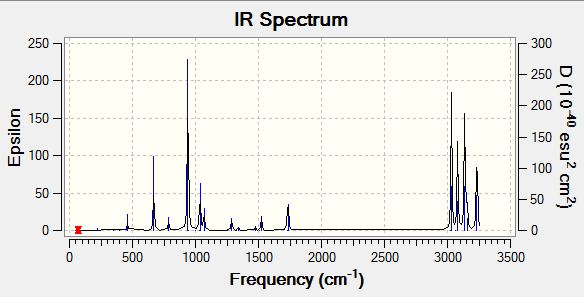
A frequency analysis was run on the B3LYP/6-31G* optimised file to the same level of theory. The low frequencies are shown below which are all low numbers and between a +/-20cm-1 range. There were no negative frequencies (imaginary frequencies) when the vibrations were visualised. The computed IR spectrum is also shown below.
Low frequencies --- -18.6345 -11.7126 -0.0009 -0.0008 -0.0006 1.8424 Low frequencies --- 72.7326 80.1452 120.0243
The output log file was visualised. Under the vibrational temperatures section under Thermochemistry were the set of energies shown below. The first of these is the potential energy at absolute zero (0 K) including the zero point vibrational energy, the second is the energy at room temperature (298.15 K) and 1 atm pressure which includes contributions from the translational, rotational and vibrational energy modes, the third contains a correction for the term RT in the enthalpy equation H=E+RT and the fourth includes the entropic contribution to the free energy.
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Transition States
To find the energies of the transitions states of this reaction it is first necessary to draw the structure correctly. An allyl fragment was drawn and optimised at the Hartree-Fock/3-21G level of theory. The checkpoint file is shown here (File:Allyl opt.chk) The optimised structure is shown below.
Opt and Freq Calculation - Chair
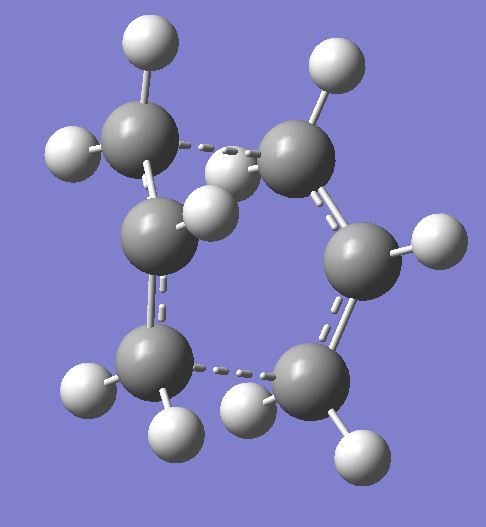
Two molecules of this optimised allyl structure were arranged into an approximate chair transition state where the distance between the terminal ends of the two allyl fragments was approximately 2.2 Å. A optimisation and frequency analysis were run on this structure. This involved using the 'optimising to a transition state' option, setting the force constants to only be calculated once and adding Opt=No Eigen into the keywords. This last keyword stops the calculation crashing if more than one imaginary frequency were to be found. The checkpoint file from the calculation is shown here (File:Chair TS 3-21G opt+freq.chk). The energy of TS was -231.61932243 a.u. and the distance between the terminal carbon atoms of the two allyl fragments was 2.020 Å. The frequency analysis correctly found an imaginary frequency at 818 cm<sup-1>-1 which is shown in an animation below on the optimised structure of the chair transition state.
Frozen Coordinate Method - Chair
Using the redundant coordinate editor the distance between the ends of the two allyl fragments from terminal carbon to terminal carbon were frozen to approximately 2.2 Å. The structure was then optimised to a minimum. The file is shown here (File:Chair guess frozen coordinate optimisation.chk) Then the bonds which had been frozen were set to optimise. The structure was set to optimise to a transition state. The checkpoint file is shown here (File:Chair guess frozen coordinate optimisation part 2.chk) The optimised structure is shown below. The energy of the TS was -231.61932198 a.u. and the terminal distance was 2.020 Å.
| Method | Energy | Terminal Bond Length |
|---|---|---|
| Opt and Freq Calculation | -231.61932243 a.u | 2.020 Å |
| Frozen Coordinate Method | -231.61932198 a.u. | 2.020 Å |
The bond lengths are the same and the energy values and very similar. Although two different methods were used both were optimised using the same basis set and so the optimised geometries are pretty much identical.
QST2 Optimisation Method - Boat
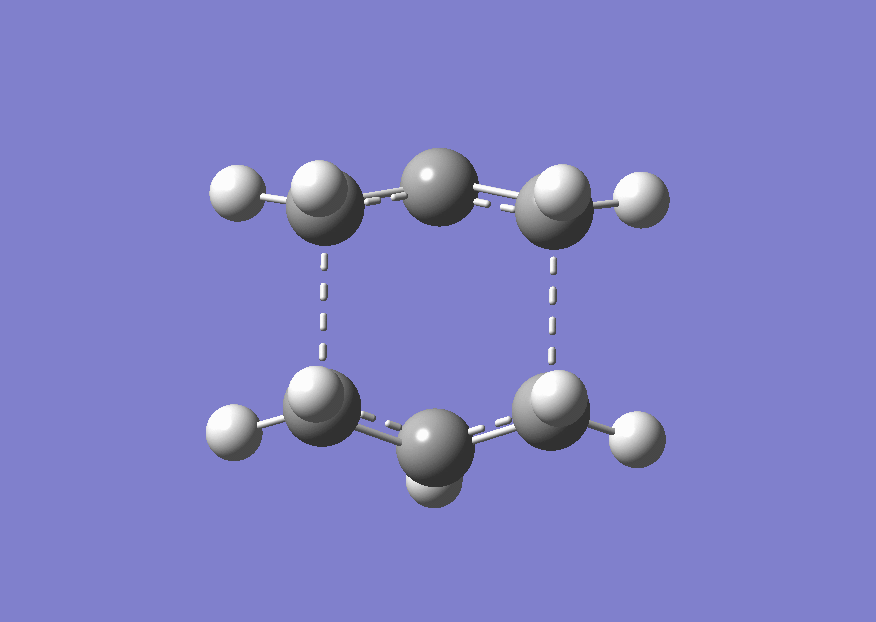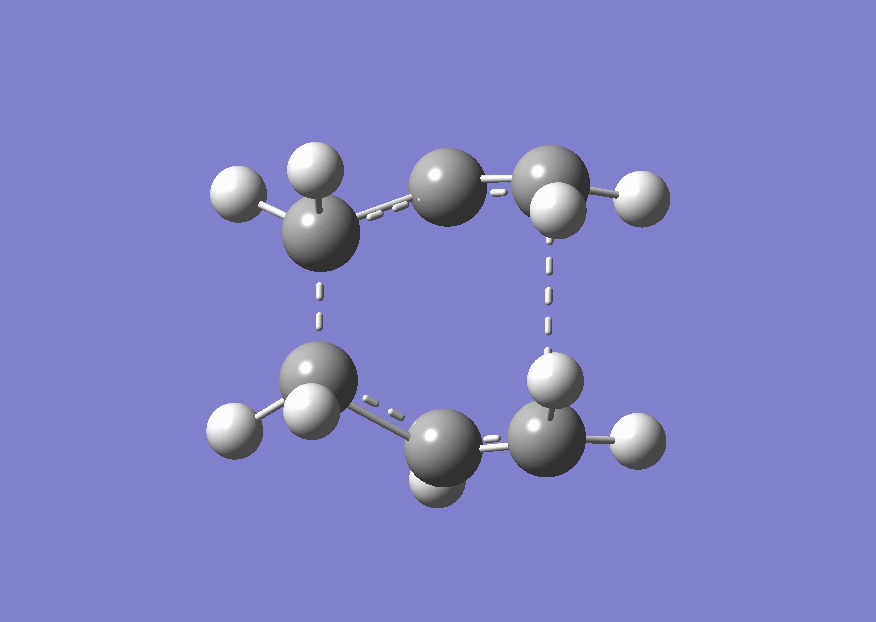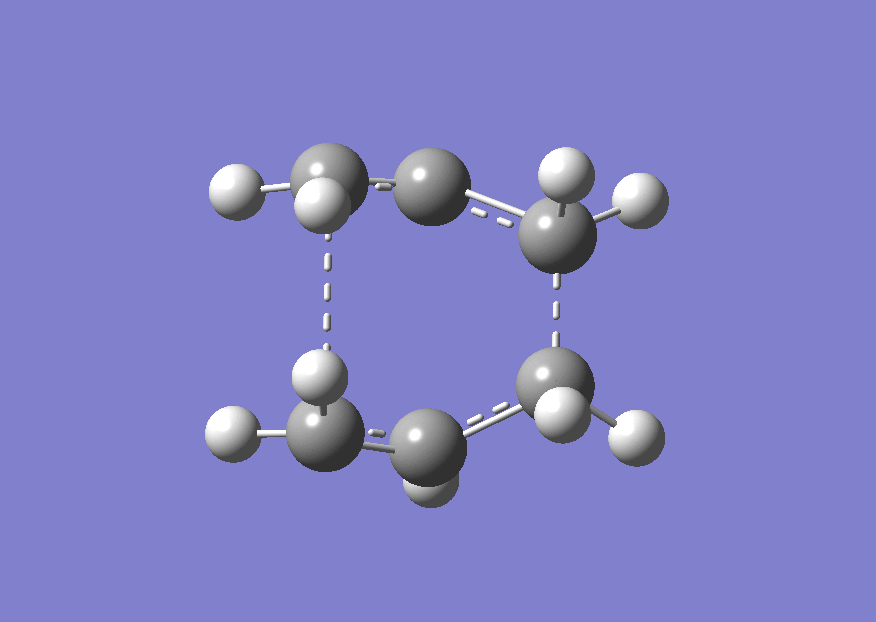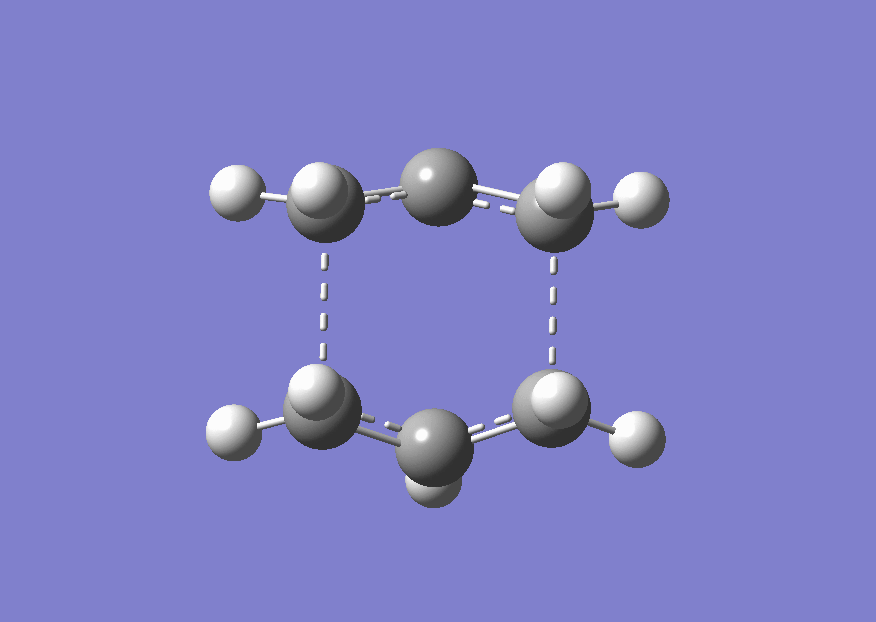
To optimise the boat TS structure a different method was used, the QST2 method. This involves defining the reactants and the products for a reaction and then running a calculation to find the transition state between them. As the reactants and products for this reaction are the same, the molecule was duplicated in a new window in the same mol group. This method only works however if the reactants and products are numbered in the same way. Although the structure does not change, the rearrangement results in the atoms being in different places. The atom list label tool was used to ensure that the reactants and products were labelled correctly taking into account the cope rearrangement. This is shown below.
A QST2 calculation was then set up to optimise to a TS with a frequency analysis. (File:Anti2 react QST2opt.chk). The structure obtained, which is shown below, was not the boat transition state but looked more like a slightly more dissociated chair.
The calculation only translated one allyl fragment with regards to the other and did not rotate around the central C-C bond. The reactants and products were redrawn to resemble the boat TS structure more closely. This was done by modifying the dihedral angles to 0o and the inside angle between the 3 outer carbons on each side to 100o. The modified reactants and products with atom labels are shown below.
The QST2 calculation was run again (File:Anti 2 altered angles QST2opt.chk) to give the boat TS shown below.
The TS had one imaginary freq at -839.39 which is animated below.
The energy of the boat transition state was -231.60280130 a.u.
Intrinsic Reaction Coordinate
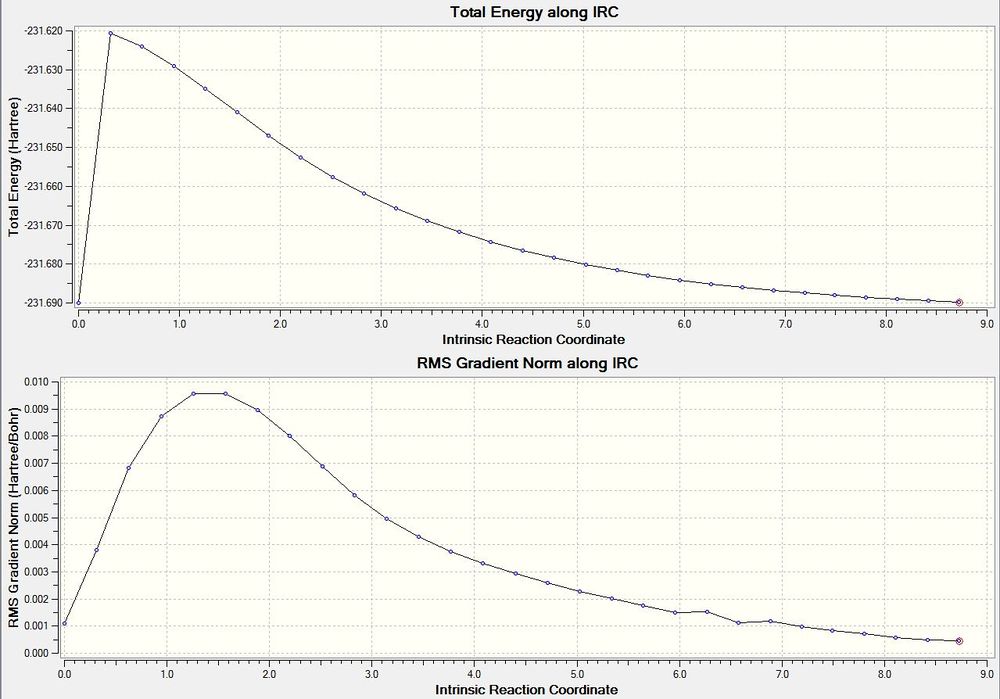
Now we have the structures of our optimsed boat and chair transition state we can look in to the reaction path from the reactants and products up to the transition states. The checkpoint file of the optimised boat structure was opened and an intrinsic reaction coordinate calculation run. As the reactants and products are the same the reaction coordinate will be identical in both directions. The calculation was just run in the forward direction. The force constants were calculated straight from the checkpoint file. The number of point computed was increase to 50 to give the calculation more time to find the minimum point. The checkpoint file from the reaction is here (File:Lmt-test.chk). The calculation crashed after 29 steps. The energy along the reaction coordinate and the root mean squared gradient over the IRC are both shown below. The structure after 29 steps is also shown below.
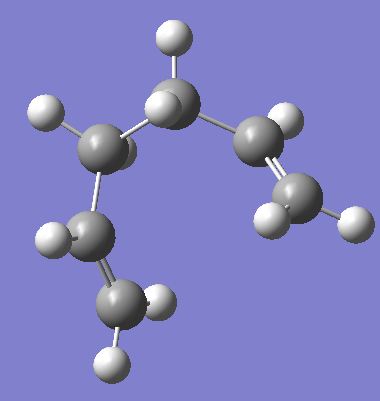
It can be seen that the structure no longer looks like a transition state and looks more like one of the minimum energy conformers of 1,5-hexadine. The energy has not reached a minimum as the RMS gradient has not reached zero and the energy value itself does not match with any of the minimum energy conformers computed earlier. However the RMS gradient is almost zero so the structure is almost at a minimum. Therefore an optimisation was run to find the minimum energy structure. The checkpoint file from this optimisation is shown here (File:Optimisation after IRC.chk). The structure and summary table from the calculation are shown below.
The energy of the conformer found corresponds to the Gauche 2 isomer found earlier. Due to the method used (which is quick) to find this it may not be the correct minimum. If the structure after the IRC was not close enough to the a local minimum, the optimisation may have ended up at the wrong minimum.
Activation Energy Calculation
The transition state structures were re-optimised from HF/3-21G to B3LYP/6-31G*. The chair file is shown here (File:Chair TS opt+freq 6-31G.chk). The energy of this TS was -234.55698303 a.u. . The boat file is shown here (File:Boat 6-31G opt.chk). The energy of this boat TS was -234.54309304 a.u. .
From the thermochemistry data in the frequency calculation log files of the boat TS, chair TS and anti 2 reactant the summary table below was formed.
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | |
|---|---|---|---|---|
| Sum of electronic and zero point energies | Sum of electronic and thermal energies | Sum of electronic and zero point energies | Sum of electronic and thermal energies | |
| 0 K | 298.15 K | 0 K | 298.15 K | |
| Chair TS | -231.466700 | -231.461341 | -234.414929 | -234.409008 |
| Boat TS | -231.450922 | -231.445291 | -234.402339 | -234.396005 |
| Anti 2 reactant | -231.539539 | -231.532565 | -234.469212 | -234.461856 |
From this table the activation energies were calculated for the two transition states at absolute zero and at room temperature. (1 a.u.=627.509kcal/mol)
| HF/3-21G Activation Energy (kcal/mol) | HF/3-21G Activation Energy (kcal/mol) | B3LYP/6-31G* Activation Energy (kcal/mol) | B3LYP/6-31G* Activation Energy (kcal/mol) | Experimental Values | |
|---|---|---|---|---|---|
| 0 K | 298.15 K | 0 K | 298.15 K | 0K | |
| Chair | 45.71 | 44.69 | 34.06 | 33.16 | 33.5 +/-0.5 |
| Boat | 55.61 | 54.77 | 41.96 | 41.32 | 44.7 +/-2.0 |
It can be seen that for both the levels of theory the boat TS had a higher activation energy and hence the boat TS is higher in energy than the chair. The values for activation energy at a B3LYP/6-31G* level of theory are much closer to the experimental values than at the HF/3-21G level of theory. This proves that B3LYP/6-31G* is a higher level basis set as the answers given are more accurate.
Diels-Alder Cycloaddition
The diels alder reaction is a [4+2] cycloaddition reaction between a diene and a dienophile. As with all pericyclic reactions it occurs via a concerted cyclic transition state. The mechanism is shown below.
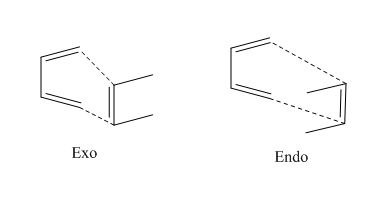
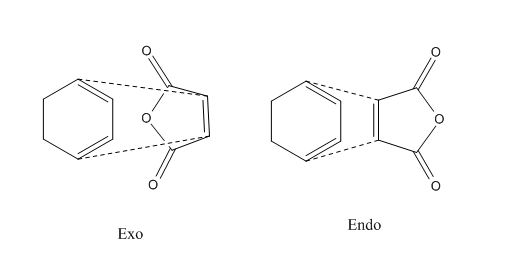
Two different set of reagents will be studied. Firstly ethene and butadiene and then the slightly more complicated case of cyclohexadiene and maleic anhydride. The is is due to endo and exo isomerisation intoduced due to the substituents on the cyclic ring. The substituents can point in towards the ring (endo) or away from it (exo). This is shown below for a simple case where an ethene molecule has two R group.
Ethene and Butadiene
Butadiene
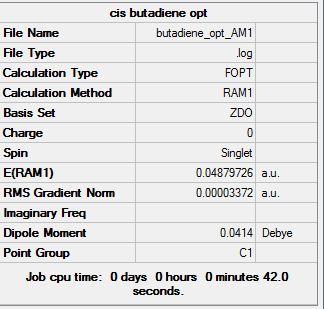
A molecule of butadiene was drawn in GaussView and optimised using the AM1 semi-empirical orbital method. (File:Butadiene opt AM1.chk). The optimised structure and summary table are shown below. The energy of the optimised molecule is 0.04879726 a.u. .
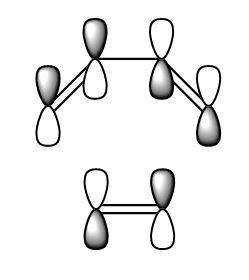
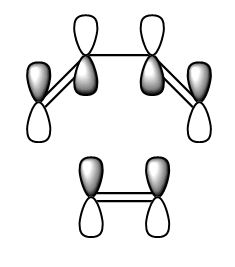
The HOMO and the LUMO were visualised and are shown below along with the accompanying LCAO drawing. The LUMO is symmetric with respect to the plane and the HOMO is anti-symmetric.
| LUMO | 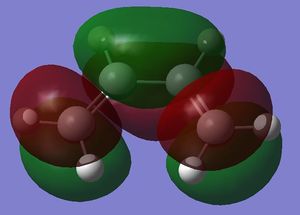 |
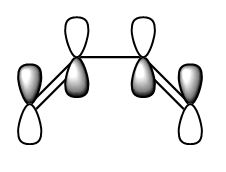 |
S |
| HOMO | 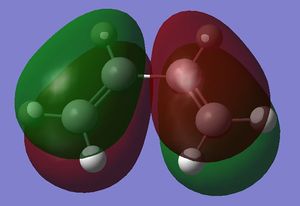 |
 |
AS |
Diels Alder Transiton State
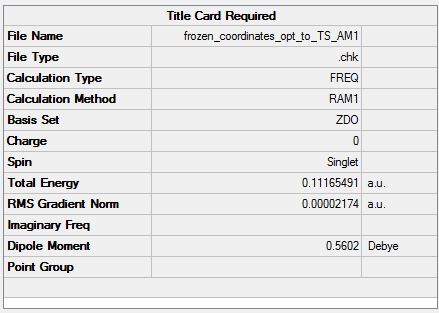
A guess of the Transition State for the diels alder reaction of butadiene and ethene was drawn in GaussView. This was based upon bicyclo octane with carbons and hydrogens removed. The bond distance between the carbons making new bonds were frozen using the redundant coordinate Editor to 2.2Å. The structure was then optimised to a minimum to a HF/6-31G level of theory (File:Frozen coordianates opt 6-31G.chk). Now the two fragments are in their optimum geometries the TS can be found. The bonds were unfrozen by changing the bonds to derivative in the redundant coordinate editor and then the structure was optimised to a TS using AM1 semi empirical molecular orbital method (File:Frozen coordinates opt to TS AM1.chk. The TS and summary table for the optimisation are shown below.
There was one imaginary frequency at -956.30. The animation is shown below. From the animation it can be seen that the formation of the two new sigma C-C bonds is synchronous i.e form at the same time. This imaginary frequency mode is very different from the first real frequency at 147.23 which appears as the two fragments rotating with respect to each other. The imaginary frequency shows bonds stretching as the fragments move closer together.
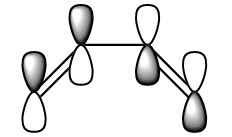
The HOMO and LUMO were visualised and are shown below. The HOMO of the diene cyclohexadiene is AS and the LUMO of ethene is also AS which is why the reaction is allowed. The interaction is in-phase and results in stabalisation.
| LUMO | 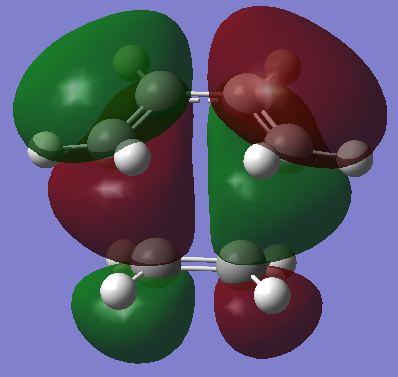 |
 |
AS |
| HOMO | 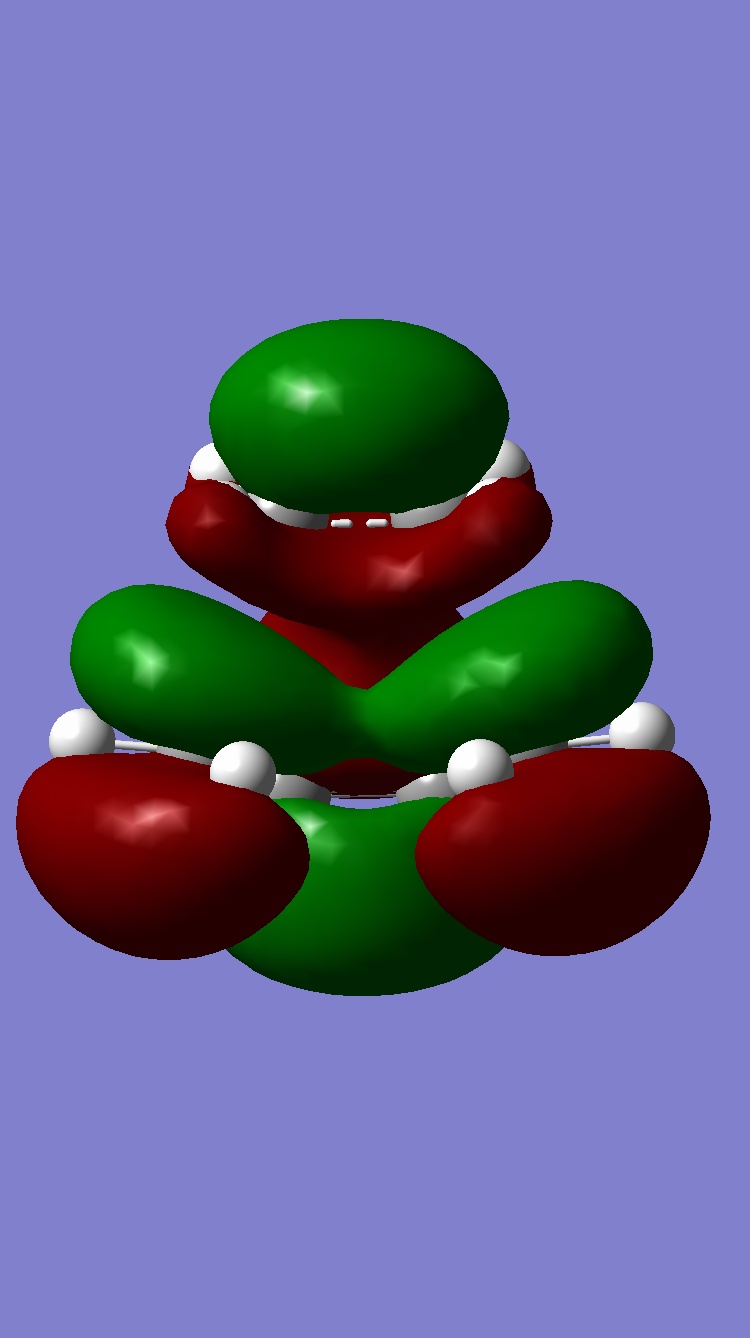 |
 |
S |
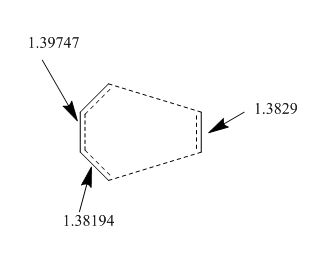
The sigma C-C bond which is forming into a pi bond and changing from sp3 to sp2 has a bond length of 1.39747 angstroms in the TS. The two bonds changing from sp2 to sp3 have bond lengths of around 1.38 angstoms. This makes sense as these bond lengths are in between the typical sp3 and sp2 bond lengths. This also indicates that there is a degree of aromaticity in the TS which fits as the reaction is pericylic and is supposed to proceed via a concerted cyclic TS.
Maleic Anhydride and Cyclohexadiene
This reaction has regioselectivity issues as there is an endo and exo product structure possible.
Maleic Anhydride
Maleic Anhydride was optimised using the AM1 semi-empirical orbital method (File:MaleicAnhydride opt AM1.chk). The optimised structure and summary table are shown below.
The Computed HOMO and LUMO are shown below along with their symmetries with regards to the reflection plane.
| LUMO | 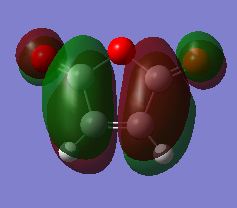 |
AS |
| HOMO |  |
S |
Cyclohexadiene
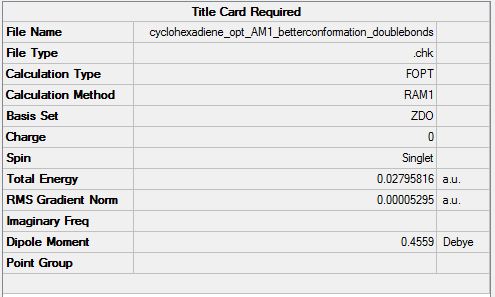
Cyclohexadiene was optimised using the AM1 semi-empirical orbital method (File:Cyclohexadiene opt AM1 betterconformation.chk). The optimised structure and summary table are shown below.
The Computed HOMO and LUMO MOs are shown below along with their symmetry with regard to the plane of reflection.
| LUMO | 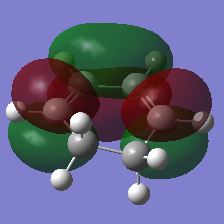 |
S |
| HOMO |  |
AS |
Endo Transition State
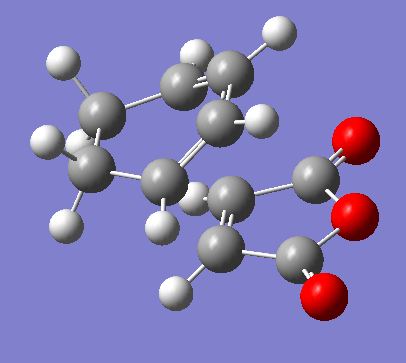
The optimised cyclohexadiene and maleic anhydride fragments were pasted into the same window on GaussView and a guess was made as to the transition state structure. The distances between the carbons which form bonds in the reaction were frozen to about 2.3Å and then the structure optimised to a minimum at a HF/3-21G level of theory (File:Frozen coord TS.chk). The bonds were then unfrozen using the derivative option in the redundant coordinate editor and the structure was optimised to TS using the AM1 empirical MO method (File:Unfrozen coord TS.chk). The optimised endo TS is shown below along with the summary table from the optimisation.
There was one imaginary frequency at -806.36 which was animated and is shown below.
Exo Transition State
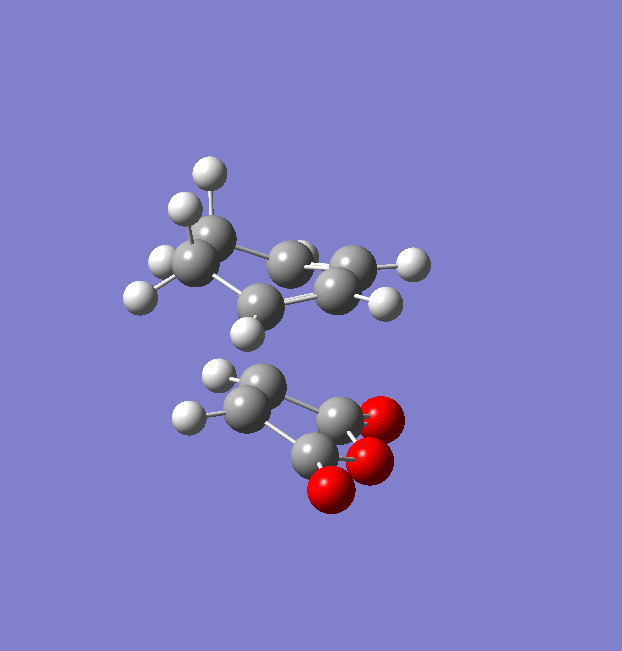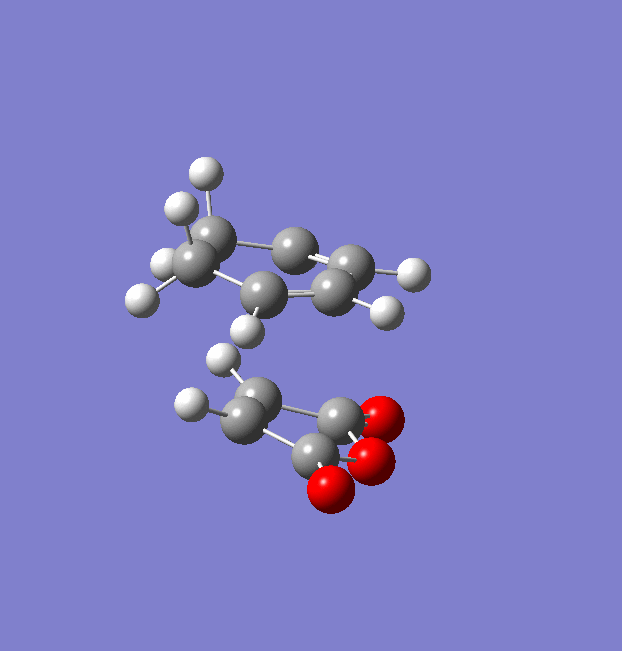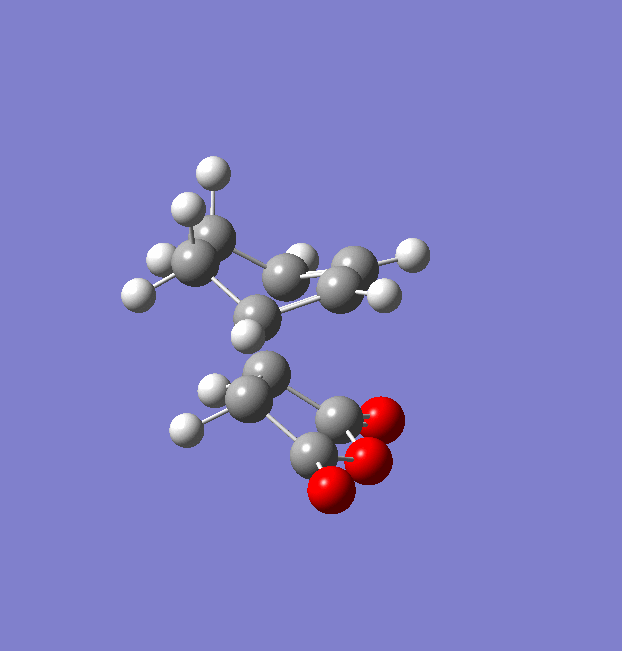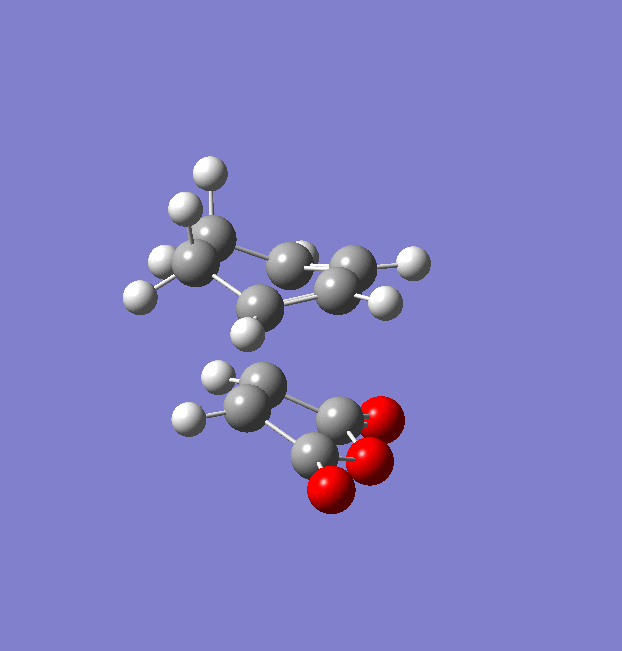
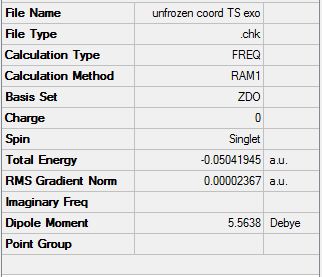
The same procedure used for the endo TS was followed to get the exo TS. The carbons which form bonds in the reaction were frozen and the structure was optimised to a minimum at a HF/3-21G level of theory (File:Frozen coord TS exo.chk). Then these bonds were unfrozen and the structure was optimised to a TS using the AM1 empirical MO method (File:Unfrozen coord TS exo.chk). The optimised exo TS is shown below along with the summary table from the optimisation.
There was one imaginary frequency at -812.22 which is animated below.
The energy of this exo TS is -0.05041945 a.u. . This is higher in energy than the endo TS which has an energy of -0.05150447 a.u. . This will result is a higher activation energy via the exo TS.
MO Analysis
The HOMO and LUMOs were visualised for the Transition states and are shown below. ALl of these are antisymmetric. The important interaction in the diels alder reaction is between the HOMO of the diene (Cyclohexadiene) and the LUMO of the dienophile (Maleic Anhydride). Both of these are AS as shown earlier which is why the reaction is allowed and why the TS for both the endo and the exo are AS. There are nodal planes in both the HOMO and the LUMO.
| LUMO | HOMO |
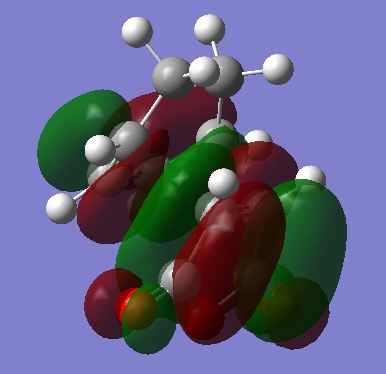 |

|
| LUMO | HOMO |
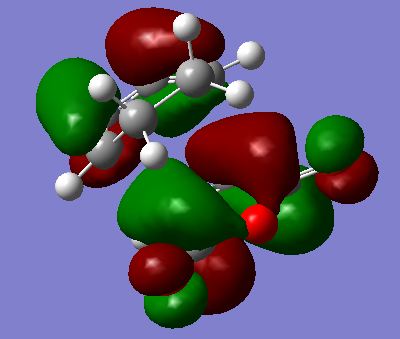 |

|
As well as the primary orbital interaction between the HOMO of the diene and the LUMO of the dienophile there is also the possibility of secondary orbital interactions. These are only possible in the endo case as shown on the diagram below. The exo conformation does nto have these possible secondary orbital interactions. As shown on the diagram the secondary orbital interactions are in phase and therefore would be a stabalising interaction. This is one possible argument as to why the endo TS is lower in energy than the exo TS. Literature'[2] however suggests that these secondary orbital effects may not actually be the reason for the endo being the lower TS, and may not even exist at all!. Looking at the HOMOs and LUMOs computed this supports the literature as the MOs which would be involved in the secondary orbital interactions do not appear to have mixed at all. Elsewhere in literature[3] it is suggested that steric crowding is a more likely reason for the higher energy endo TS. Looking at the two structures it can be seen that in the exo structure the oxygens in maleic anhydride can clash with two methyl groups whereas in the endo form the oxygens can only clash with hydrogens. This steric clashing raises the energy of the exo TS relative to the endo TS.
References
- ↑ A.C. Cope, E.M. Hardy, J. Am. Chem. Soc., 1940, 62, 441
- ↑ J. I. García, J A. Mayoral and L. Salvatella, Acc. Chem. Res., 33, 658-664, 2000 DOI:10.1021/ar0000152
- ↑ M. A. Fox, R. Cardona and N. J. Kiwiet, J. Org. Chem., 52 (8), 1469–1474, 1987 DOI:10.1021/jo00384a016