Rep:Mod:jamie
Introduction
GaussView was used to perform optimisations, frequency analyses, population analyses and to generally probe into different molecular structures. A week was spent investigating small molecules such as BH3 and TlBr3 and then a mini project looking into Main Group Halides was undertaken in the second week.
BH3
Optimisation of BH3
A molecule of BH3 was created in GaussView by fixing a boron atom in space and extending the B-H bond lengths to 1.5Å.
The molecule was optimised using the method B3LYP and the basis set 3-21G. The B3LYP method determines the approximations which are are made in the solving of the Schrodinger equation. The basic set determines the accuracy. 3-21G has a very low accuracy but makes the calculations very quick.
The data for the optimised BH3 molecule is shown below in .log format.
The optimisation data is summarised below in a table, showing the optimum position of the nuclei for the given electronic configuration.
| ||
| File Name | bh3 | |
| File Type | .log | |
| Calculation Type | FOPT | |
| Calculation method | RB3LYP | |
| Basis Set | 3-21G | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -26.46226338 a.u. | |
| RMS Grad. Norm. | 0.00020672 a.u. | |
| Dipole Moment | 0 Debye | |
| Point Group | D3H | |
| B-H Bond Length | 1.19Å | |
| H-B-H Bond Angle | 120° | |
| Job Time | 10.0s | |
The bond angles have optimised to 1.19349Å which is close to the literature value of 1.19Å [1] The gradient has a value lower than 0.001 and is tending towards zero so suggests that the optimisation is complete. To further check that the optimisation is complete we can look at the 'real' text based .log file, which is shown below. This shows us that the forces have converged, where force is the gradient of the energy vs distance graph. It also shows that the placements of the atoms have converged. This means that for a small displacement the energy does not change (within a small amount).
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
When molecule is being optimised we are solving the Schrodinger equation under the Born-Oppenheimer approximation for the electrons in our molecule, assuming fixed positions of our nuclei. The energy obtained is dependent on the nuclear positions so the energy E(R) can be represented in terms of a collective coordinate R. If the nuclei positions are moved slightly then the energy obtained will vary also as the interactions inside the molecule will change.
This gives us a dissociation curved which is very similar to the Morse potential used for a diatomic. As R decreases the atoms get closer together and the repulsion causes the energy to go up. As R increases the nuclei become stretched and the electrons no longer form a bond. This decreases the nuclear attraction and the energy goes up. The minimum point on a Morse potential curve is the compromise between these two forces and is when the system is in equilibrium. At this point the molecule will have its equilibrium bond length.
Therefore when we are optimising a molecule we are looking for this equilibrium point. We solve the Schrodinger equation for the nuclear positions and electrons to find E(R). We then move the atoms from this original position a little to obtain a different E(R). If the new energy is lower then we continue to move in that direction, if not then we move in the other direction. We gradually move closer and closer towards the equilibrium point, traversing the PES, until the lowest energy point is reached and optimisation is complete.
The Total Energy curve below shows the program traversing the potential energy surface for the BH3 molecule in order to find the structure with the lowest energy.
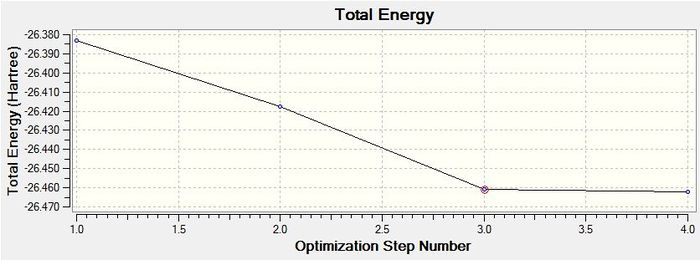
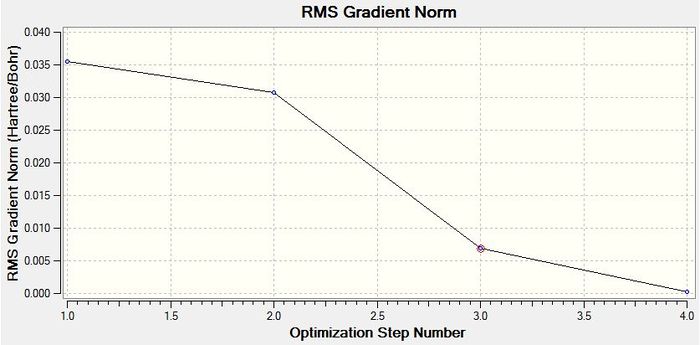
The graph below is the Root Mean Squared gradient and shows how the gradient goes to zero as we approach the minimum energy point. When the molecule is in the potential energy well it experiences no forces trying to shift it one way or another. When the molecule is not in equilibrium it will be experiencing forces, such as nuclear-nuclear replulsion, nuclear-electron attraction and electron-electron attraction, which cause the molecule to shift positions. Force can be represented as F=-dE/dR. This shows that the gradient from our calculation is the force between the atoms. When this force is zero the gradient is also zero and we know that the molecule has reached the bottom of the potential energy well. This explains why the molecule has optimised fully when the gradient goes to zero.
The movie below shows the four steps of the optimisation of BH3. It can be seen that the original conformation of the molecule does not show bonding liens between the atoms but by the end conformation it does show these. This highlights the issue of 'when is a bond a bond?'.
GaussView draws bonds based on a pre-determined distance criteria. So the fact that GaussView has not drawn a bond does not mean that the bond does not exist. It just means the the distance between the atoms exceeds the pre-defined bond distance.
A bond is described as the overlap of electron density. Orbitals of electron density from one atom overlap with orbitals of electron density from another to form a stabalised (lower-energy) structure with a covalent bond. This bond corresponds to the minimum on the Morse Potential as explained earlier. GaussView only takes the simple distance view into account when deciding if to form a bond and does not take into account the more complex orbital picture.
Optimisation using 6-31G(d,p)
BH3 was optimised again using a better basis set, 6-31G(d,p). The dat in .log format is below.
File:BH3 OPTIMISED WITH 6-31G.LOG
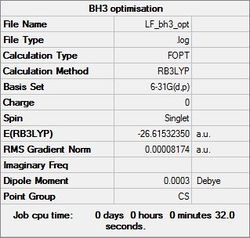
The table below summarises the information obtained from the optimisation.
| File Name | BH3 optimised with 6-31G |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61532363 a.u. |
| RMS Grad. Norm. | 0.00000235 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| B-H Bond Length | 1.19Å |
| H-B-H Bond Angle | 120° |
| Job Time | 9.0s |
The B-H Bond length is also close to the literature value of 1.19Å[1]. The value seems to be closer to the literature value than for the 3-21G optimised B-h bond length. However it is impossible to compare the two values to each other as they have been obtained using completely different basis sets.
The item table below confirms that the optimisation converged.
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000019 0.001800 YES RMS Displacement 0.000012 0.001200 YES Predicted change in Energy=-1.304899D-10 Optimization completed.
TlBr3
A molecule of TlBr3 was drawn and the symmetry restricted to D3H. Thalium has 81 electrons and bromine 35 electons. This is a lot more electrons than in BH3 example and makes the quantum mechanics much harder. Not only this but both atoms exhibit relativistic effects which can't be recovered using the standard Schrodinger equation. Hence we need to use a pseudo-potential to optimise the molecule. For this the assumption is that the valence electrons dominate bonding interactions and that the core electrons of an atom can be modelled safety using this pseudo fucntion. The molecule was set up to optimise using the B3LYP method with the basis set LanL2DZ. This calculation was submitted to the Departmental SCAN cluster to optimise. Once the calculation was finished it was published to the chemical data D-Space. The link can be found below.
The .log was visualised using GaussView and the key information from the optimisation summarised in the table below.
| File Name | logfile tlbr3 from hpc |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -91.21812851 a.u. |
| RMS Grad. Norm. | 0.00000090 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| Tl-Br Bond Length | 2.65Å |
| Br-Tl-Br Bond Angle | 120° |
| Job Time | 7.0s |
The optimised bond length was close to the literature value of 2.52Å[2].
The item table was checked to confirm convergence.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.083982D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
BBr3
BBr3 contains both heavy bromine atoms which require pseudo-potentials and a light boron atom which can be treated more accurately witha full basis set. Hence we need to mix the two. The 6-31G(d,p) optimised BH3 file was reopened and the hydrogen atoms replaced with bromine atoms. A calculation was setup with method GEN and 'pseudo=read gfinput' written in the additional keywords section to enable the option to specify pseudo potentials for atoms individually. Then in notepad the file was altered manually to specify these basis sets for each atom(6-31G(d,p) for boron and LanL2DZ for bromine).
The file was sent to the HPC to optimise and then published to d space. The link to d space is below.
A picture of the optimised molecule, a table summarising key information and the item table are shown below. The bond length of 1.93396Å is close to the literature value of 1.893Å[1]
| File Name | logfile from hpc BBr3 |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation method | RB3LYP |
| Basis Set | Gen |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -64.43645296 a.u. |
| RMS Grad. Norm. | 0.00000382 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| B-Br Bond Length | 1.93Å |
| Br-B-Br Bond Angle | 120° |
| Job Time | 7.0s |
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.027599D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.934 -DE/DX = 0.0 !
! R2 R(1,3) 1.934 -DE/DX = 0.0 !
! R3 R(1,4) 1.934 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Structure Comparison
| Molecule | Bond Distance (Å) |
| BH3 | 1.19 |
| BBr3 | 1.93 |
| TlBr3 | 2.65 |
As the ligand is changed from hydorgen to bromine in the born molecules it can be seen that teh bond length increases from 1.19232Å to 1.93396Å. Bromine is bigger and has more diffuse orbitals than hydrogen. Therefore the orbitals overlap less with the orbitals of boron, there is less bonding and the bond length increases. As the central atom is changed from Boron to Thallium, keeping the bromine ligands, the bond distance increase from 1.93Å to 2.650Å. Again Thallium is larger than Boron so has much more diffuse outer electrons. The density of the overlap is low and so there is lowere bonding and a longer bond length.
Hydrogen and born are both one electron donating ligands so form similar bonds. Bromine is much more electronegative and forms more polar bonds. Boron and Thallium are both in group 3 of the periodic table so from 3 covalent bonds to hydrogen or bromine.
Frequency Analysis
It was shown earlier that the gradient of the PES relates to the force between atoms. When this gradient is zero the forces acting on the atoms are balanced and the structure is in equilibrium. However this does not tell us whether the point is a maxima or a minima. A first derivative of zero can correspond to a minimum energy point of a structure or to a transition state if it is a maxima. To calculate which on of these we have we can take the second derivative of the potential energy surface. Positive values will correspond to minima and negative values to maxima. A frequency analysis essentially involves doing just this and taking the second derivative of the PES. If all the frequencies are positive we have a minimum energy point for our structure and if we have a negative value then we have a transition state. If there is any more than one negative value then the critical point has not been found and the optimisation has not worked!
BH3
The 6-31G(d,p) optimised BH3 was re-opened and the calculation job type set to frequency. Once this had run the energy was checked and this matched with the optimisation calculation for this same molecule. The .log file, the summary table and the item table are shown below.
File:JAMESGOODCHILD BH3 FREQ.LOG
| File Name | JAMESGOODCHILD_BH3_FREQ |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61532363 a.u. |
| RMS Grad. Norm. | 0.00000237 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| B-H Bond Length | 1.19Å |
| H-B-H Bond Angle | 120° |
| Job Time | 12.0s |
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000002 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Ehttps://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:jamie&action=edit§ion=9nergy=-1.323374D-10
Optimization completed.
-- Stationary point found.
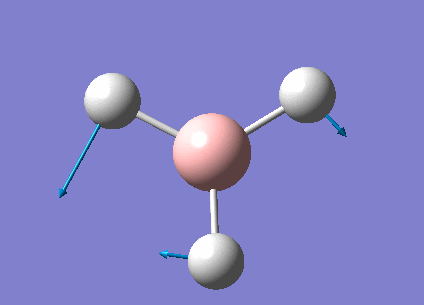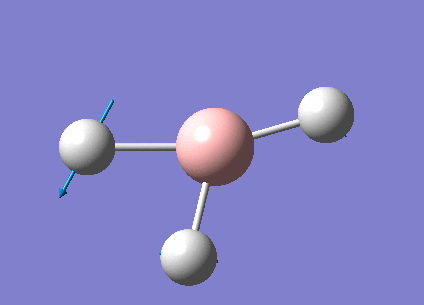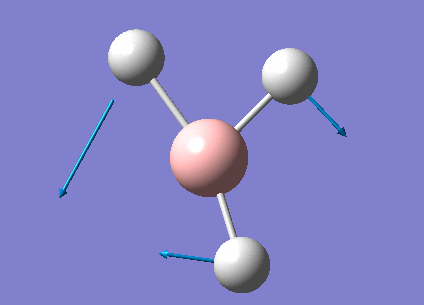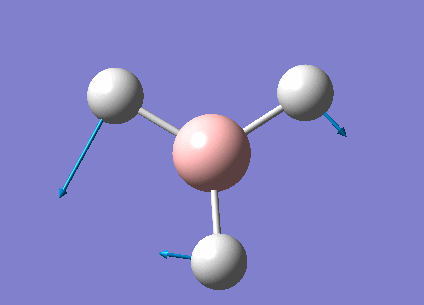
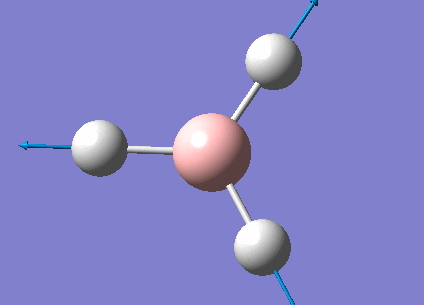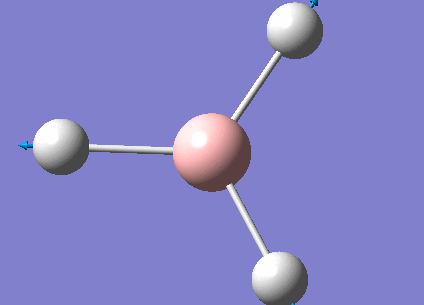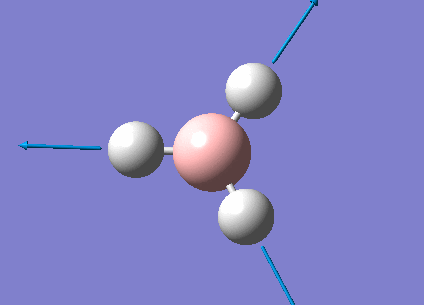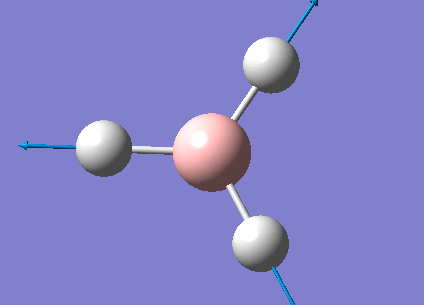
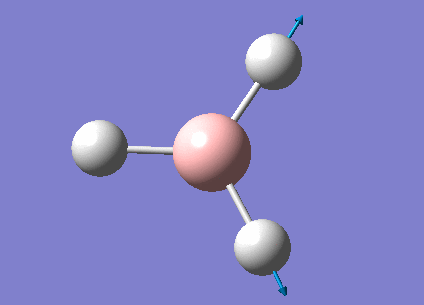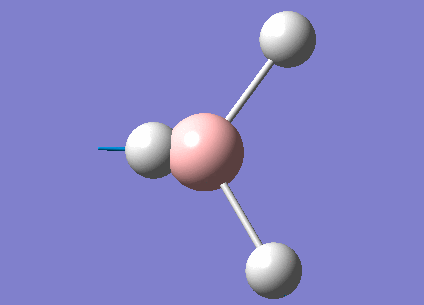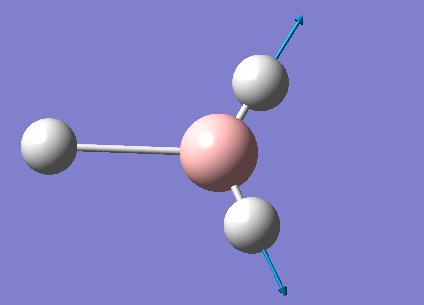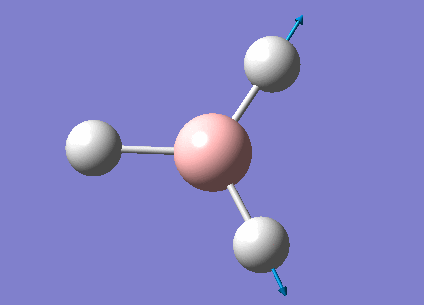
The real output file shows the following low frequencies. Molecules have 3N-6 vibrational frequencies. The 6 low numbers on the top row (between -1 and 13) correspond to the "-6" which are the motions of the centre of mass of the molecule. These values relate to the method employed to carry out the frequency analysis. The closer to zero they are the better the method used. The values are within +/-15cm-1 which is close enough to zero to continue with our analysis. There are much larger 'real' vibrational frequencies shown on the bottom row.
Low frequencies --- -0.9033 -0.7343 -0.0054 6.7375 12.2491 12.2824 Low frequencies --- 1163.0003 1213.1853 1213.1880
Animated BH3 frequencies
| No. | Animated File | Frequency(cm-1) | Intensity | Symmetry D3H point group | Description of Vibration |
| 1 |  |
1163 | 93 | A2" | All 3 hydrogen atoms bending symmetrically |
| 2 |  |
1213 | 14 | E' | 1 hydrogen atom is stationary and 2 hydrogen atoms are bending symmetrically in the plane of the molecule (scissoring) |
| 3 |  |
1213 | 14. | E' | All 3 hydrogen atoms are bending asymmetrically to each other in the plane of the molecule (in plane rocking) |
| 4 |  |
2582 | 0.0000 | A1' | All 3 hydrogen atoms are stretching symmetrically |
| 5 |  |
2715 | 126 | E' | 1 hydrogen is stationary and 2 hydrogen atom are stretching asymmetrically in the plane of the molecule |
| 6 |  |
2715 | 126 | E' | 2 hydrogen atoms are stretching symmetrically with each other, while the other is stretching asymmetrically to these 2 |
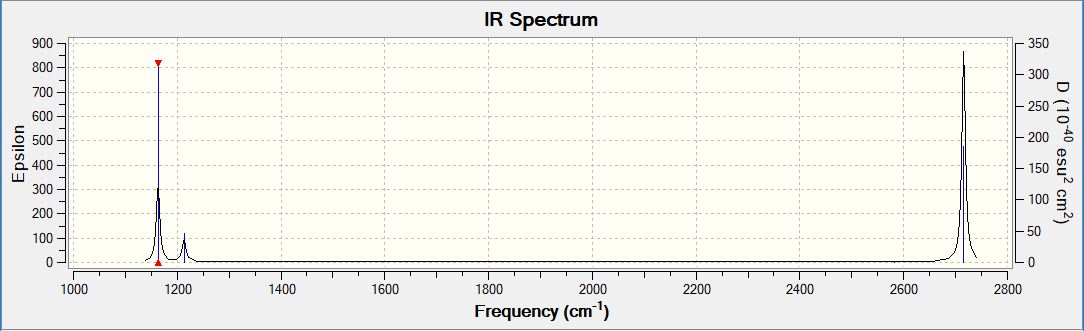
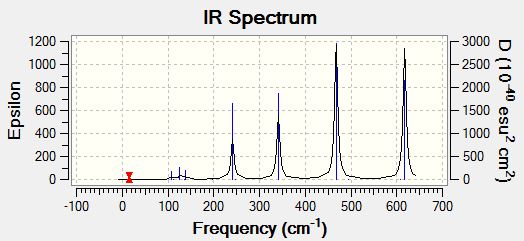
Infrared spectrum from GaussView
Above is a computed IR spectrum of BH3 from GaussView. Although there were shown to be 6 stretching frequencies, there are clearly only 3 peaks in this spectrum. There are two reasons for this. Firstly the vibration at 2582.26 shows no change in dipole moment. Therefore it is not IR active and there is no shift at this frequency. The second reason is due to degenerate vibrations. Vibrations 1 and 2 vibrate at the same frequency so are observed as just one peak in the spectrum at 1213.19. This is also true of vibrations 5 and 6, which cause one peak at 2715.43.
TlBr3
The optimised TlBr3 file from earlier was opened and a frequency analysis run on it on the HPC. The results were puplished on D-space and can be seen here. DOI:10042/23731
The summary table, item table and low frequency information can be seen below.
| File Name | tlbr3 frequency file from hpc |
| File Type | .log |
| Calculation Type | FREQ |
| Calculation method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -91.21812851 a.u. |
| RMS Grad. Norm. | 0.00000088 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| Tl-Br Bond Length | 2.65Å |
| Br-Tl-Br Bond Angle | 120° |
| Job Time | 15.3s |
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000011 0.001200 YES
Predicted change in Energy=-5.660901D-11
Optimization completed.
-- Stationary point found.
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
From the item table it can be seen that the procedure converged and the molecule was optimised. The Low frequencies are all positive which confirms that we have found a minimum and in the correct range.
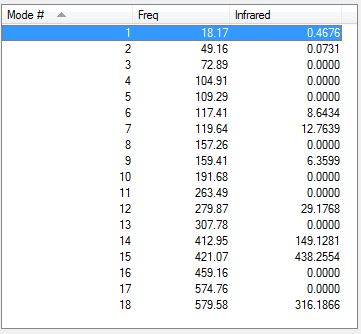
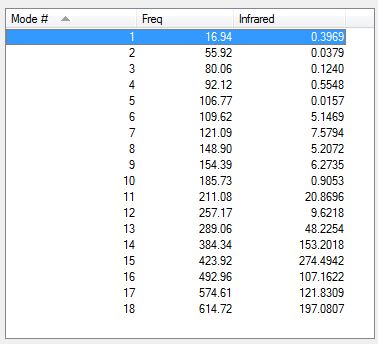
Below is a table summarising the vibrational frequencies of TlBr3.
| No. | Animated File | Frequency(cm-1) | Intensity | Symmetry D3H point group | Description of Vibration |
| 1 |  |
46 | 4 | E' | 1 bromine is stationary and the other two are bending symmetrically in the plane of the molecule (scissoring) |
| 2 |  |
46 | 4 | E' | 1 bond to bromine is bending while the other two stay stationary (in plane rocking) |
| 3 |  |
52 | 6 | A2" | 3 bromine atoms bending symmetrically at 90o to the plane of the molecule |
| 4 |  |
165 | 0.0000 | A1 | All 3 bromine atoms are stretching symmetrically in the plane of the molecule |
| 5 |  |
210 | 25 | E' | 1 bromine atom is stationary while the other 2 are stretching asymmetrically in the plane of the molecule |
| 6 |  |
210 | 25 | E' | 2 bromine are stretching symmetrically to each other and the other asymmetrically with regards to these two |
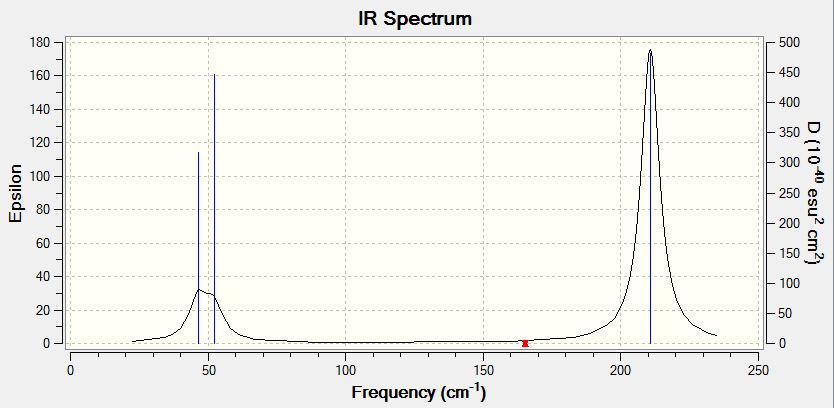
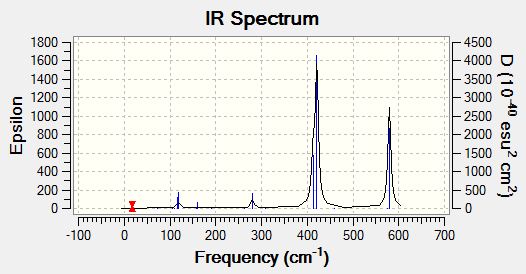
Below is the infrared spectrum as computed by GaussView.
Comparing frequencies of TlBr3 and BH3
| Number | Frequency of TIBr3(cm-1) | Frequency of BH3(cm-1) |
|---|---|---|
| 1 | 46.43 | 1163 |
| 2 | 46.43 | 1213 |
| 3 | 51.14 | 1213 |
| 4 | 165.27 | 2582 |
| 5 | 210.869 | 2715 |
| 6 | 210.869 | 2715 |
In general the vibrational frequencies for BH3 are much larger than for TlBr3. The reduced mass of BH3 is much lower which corresponds to a larger vibrational frequency. The modes have reordered in terms of their relative energies. The vibration numbers in the table above do not match up for both molecules as some have swapped around. Both spectra have 3 visible modes. More are not seen due to the effects of degeneracy and no change in dipole moments.
The same method and basis set must be used for both the optimisation and the frequency analysis calculations because the frequency analysis must be carried out on the exact same PES as the optimisation. Otherwise the two calculations do not correlate and cannot be used for comparison. The methods and basis sets used for both molecules must be the same or they cannot be compared. If different basis sets are used then different assumptions have been made and the energy outputs are not comparable for two different molecules.
Frequency calculations are carried out so that we can ensure we have reached a minimum point in the potential well. Also we can obtain information on the vibrational frequencies of the molecule which can be used to predict or compare with experimental IR data.
Low frequencies represent the '-6' vibrations from 3N-6 equations which show the vibrations of the centre of mass of the molecule.
Molecular Orbital Analysis of BH3
A population analysis was run in the HPC and published to D-Space.DOI:10042/23807
The summary table is shown below.
| File Name | bh3 checkpoint file from hpc for MO energies |
| File Type | .log |
| Calculation Type | SP |
| Calculation method | RB3LYP |
| Basis Set | 6-31G(D,P) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61532363 a.u. |
| RMS Grad. Norm. | 0.00000000 a.u. |
| Dipole Moment | 0 Debye |
| Point Group | D3H |
| B-H Bond Length | 1.19Å |
| H-B-H Bond Angle | 120° |
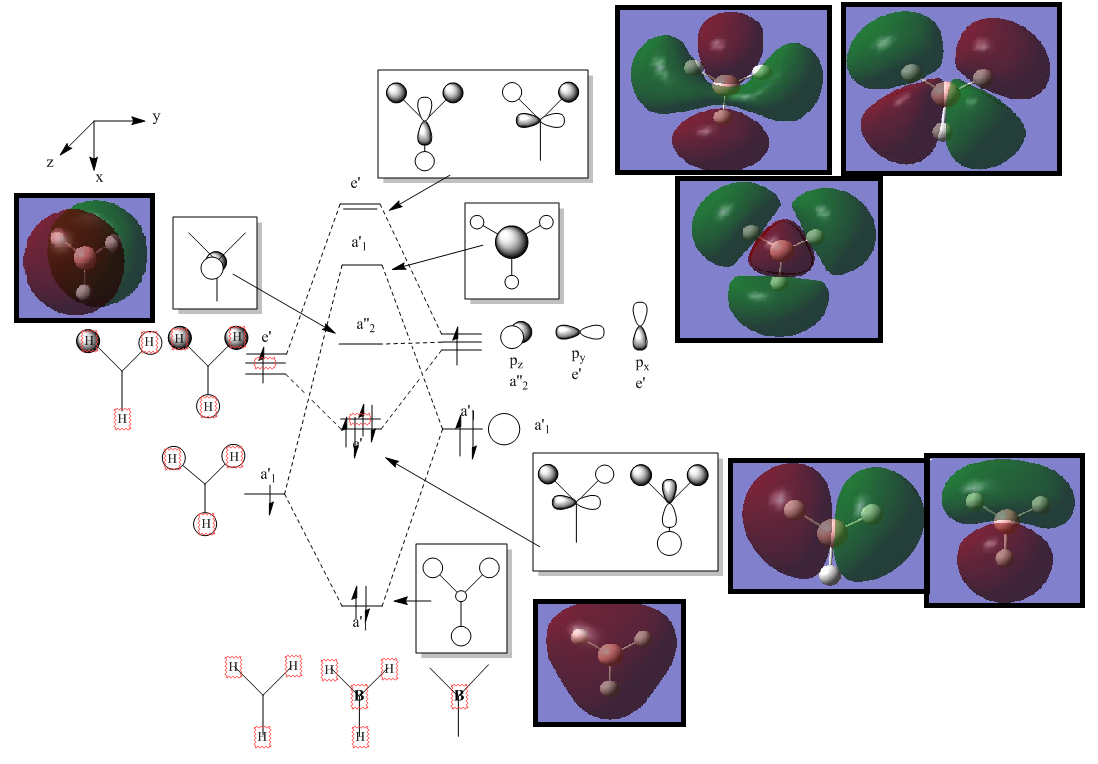
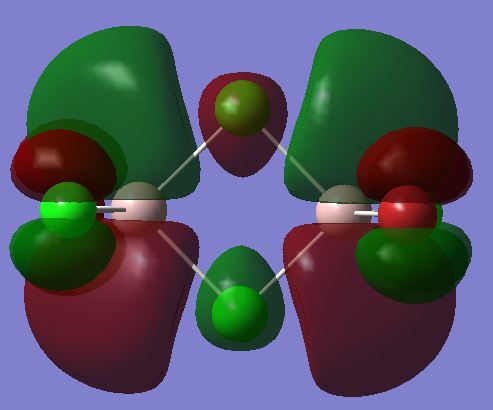
A MO diagram, calculated vwith the LCAO method, is shown below.
There is a lower a1' orbital which has not been included on the diagram as it is lower in energy. The Ccomputed MO is shown below.
It can be seen from the MO diagram above that the computed MO's match up very well with the Mo's calculated using LCAO. This suggests that qualitative MO theory using LCAO can provide very accurate results. It is useful as it takes much less time and computing power than calculating the real MO's but gives results which are nearly as accurate.
NH3
Optimisation
A molecule of NH3 was optimised using the basis set 6-31G(d,p). The .log file, summary table, physical information and item table are shown below.
File:NH3 OPTIMISATION 631GDP.LOG
The bond length was 1.01800Å was close to the literature value of 1.01Å[3]. The H-N-H bond angle was 105.748o.
Item Value Threshold Converged?
Maximum Force 0.000200 0.000450 YES
RMS Force 0.000124 0.000300 YES
Maximum Displacement 0.000386 0.001800 YES
RMS Displacement 0.000261 0.001200 YES
Predicted change in Energy=-1.088492D-07
Optimization completed.
-- Stationary point found.
Frequency Analysis
A population analysis was run on NH3. The .log file, summary table, item table and low frequencies are shown below.
Item Value Threshold Converged?
Maximum Force 0.000022 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000080 0.001800 YES
RMS Displacement 0.000039 0.001200 YES
Predicted change in Energy=-1.634400D-09
Optimization completed.
-- Stationary point found.
The item show that the molecule was optimised as the forces and atomic placements have converged.
Low frequencies --- -6.9976 0.0009 0.0014 0.0016 11.3042 16.1325 Low frequencies --- 1089.3539 1693.9212 1693.9581
There are no negative frequencies which shows that we have found a minimum. All the '-6' low frequencies are low and in the correct range.
Animation of frequencies
| No. | Animated File | Frequency(cm-1) | Intensity | Symmetry D3H point group | Description of Vibration |
| 1 |  |
1089 | 145 | E' | All 3 hydrogens bending symmetrically |
| 2 |  |
1693 | 14 | E' | 2 hydrogens scissoring and 1 bending asymmetrically to the others |
| 3 |  |
1693 | 13.5552 | A2" | 2 hydrogens scissoring and the other rocking back and forth |
| 4 |  |
3461 | 1 | A1' | All 3 hydrogens bending symmetrically |
| 5 |  |
3589 | 0 | E' | 2 hydrogens stretching symmetrically with each other and the other stretching asymmetrically with regards to the other two. |
| 6 |  |
3589 | 0. | E' | 1 hydrogen is stationary while the other two are stretching asymmetrically with each other |
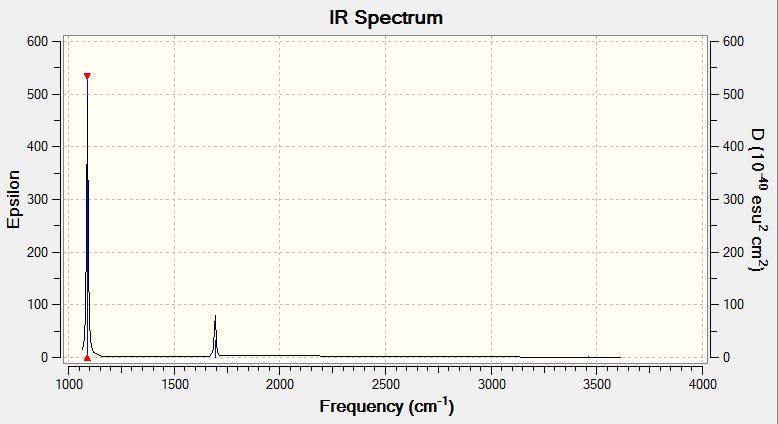
IR Spectrum
Although there are 6 vibrations, again not all of these can be seen in the spectrum. This is due to vibrations 4,5 and 6 having very small changes in dipole moment so they cannot be seen in the spectrum. Vibrations 2 and 3 have almost degenerate frequencies so appear as one peak on the spectrum.
Population Analysis
A population analysis was performed on NH3</sub and the .log file is here. File:NH3 POPULATION 631GDP.LOG
The summary table is shown below.
The eight lowest computed MO's are shown below (from lowest energy to highest energy as you go along the lines from left to right). The 5th MO is the HOMO and the 6th is the LUMO.
NBO Analysis
A Natural Bond Orbital Analysis was performed on the .log file from the optimisation of NH3. The charge distribution is shown below in a diagram and a summary table. The charge range is from -1.125 (bright red) to +1.125 (bright green). The charge for the electronegative nitrogen atom is -1.125 and +0.375 for the hydrogen atoms.
NH3BH3
Optimisation
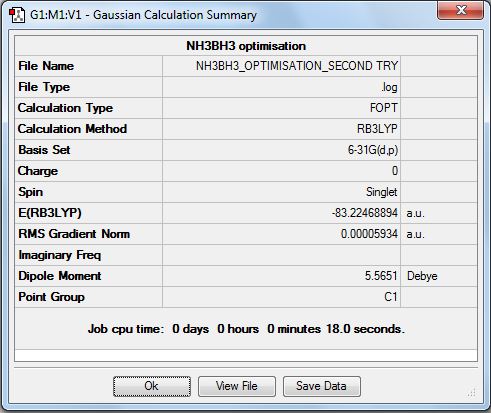
An optimisation was run on a molecule of NH3BH3 using the B3LYP method and the 6-31G (d,p) basis set. The log file is here (File:NH3BH3 OPTIMISATION.LOG).
The summary table is shown below.
Item Value Threshold Converged? Maximum Force 0.006597 0.000450 NO RMS Force 0.001351 0.000300 NO Maximum Displacement 0.024642 0.001800 NO RMS Displacement 0.006715 0.001200 NO Predicted change in Energy=-1.406360D-04
The above item table shows that the optimisation did not converge and is not complete. Therefore the same calculation was run again. The .log file is here(File:NH3BH3 OPTIMISATION SECOND TRY.LOG)
The summary table is shown below.
The item table below shows that the calculation converged the second time.
Item Value Threshold Converged?
Maximum Force 0.000121 0.000450 YES
RMS Force 0.000057 0.000300 YES
Maximum Displacement 0.000537 0.001800 YES
RMS Displacement 0.000294 0.001200 YES
Predicted change in Energy=-1.625656D-07
Optimization completed.
-- Stationary point found.
Frequency Analysis
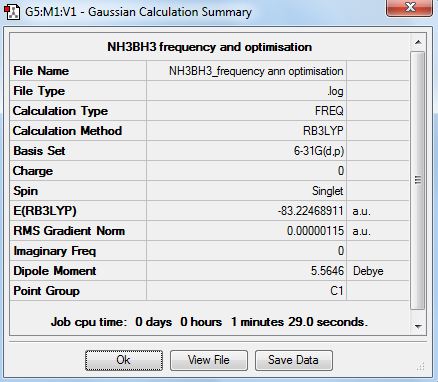
A frequency analysis was performed on he optimised file using B3LYP and the 6-31G(d,p) basis set. tHe .log file is here (File:NH3BH3 FREQUENCY ANN OPTIMISATION.LOG) The summary table is shown below.
The low frequencies are shown below. There are no negative values so a minimum was found. They also all fit into the +/-15cm-1 range.
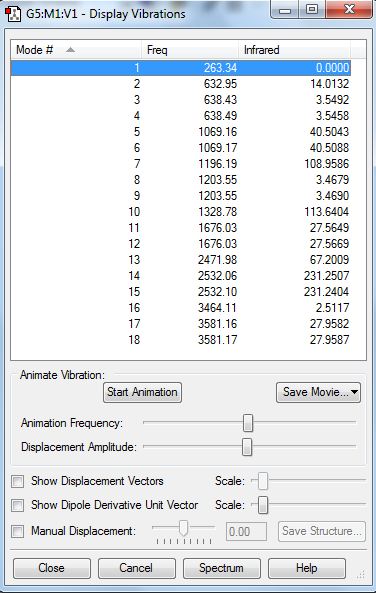
Low frequencies --- -3.2037 -2.9009 -0.0010 -0.0008 -0.0006 3.6115 Low frequencies --- 263.3430 632.9540 638.4329
The vibration frequencies are shown below.
Energy Comparisons
The energies of NH3BH3, NH3 and BH3 are compared in the table below.
| molecule | energy (a.u) |
|---|---|
| NH3 | -56.55776872 |
| BH3 | -26.61532363 |
| NH3 BH3 | -83.22468911 |
The values in the table above were used to calculate the dissociation energy of ammonia borane. This is shown below.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] ΔE=-83.22468911-[-56.55776872+(-26.61532363)] ΔE=-0.05159676 a.u ΔE=-135.5kJ/mol
The energy calculated is the value for the association of NH3 and BH3 in to NH3 BH3. It is also the dissociation energy of NH3 BH3. The value is lower than the literature value of -172.1 kJ mol-1[4]. Thic could possibly be down to the assumptions associated with the basis sets used.
Mini Project - Lewis Acids and Bases
Firstly a preliminary optimisation was run to ensure the molecule drawn was in the correct conformation. This was done for each of the four isomers of Al2Cl4Br2 and was done using the B3LYP method with just the low basis set 3-21G. Then a higher basis set with pseudo potentials was used to perform a more accurate optimisation. The B3LYP method was used for the Aluminium and Chlorine atoms along with the basis set 6-31G(d,p). The pseudo set LANL2DZdp was used for the bromine atoms. These were used for both the optimisations and the frequency calculations. The data for the four isomers of Al2Cl4Br2 is shown below.
Optimisation Calculations
Isomer 1 [Cis-BrClAl(µ-Cl2)AlClBr]
The isomer is shown below and has symmetry C2v.
The first optimisation with the 3-21G basis set is linked here. DOI:10042/23996
The first time the higher level basis sets were used with the pseudo potentials the optimisation did not converge. The file is shown here DOI:10042/24000
The optimised file was re-run with the same pseudo potentials and it converged this time. The D-space link is here DOI:10042/24006 . The summary file is shown below.
It can be seen from the item table below that the force and displacements converged.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000002 0.000060 YES
RMS Displacement 0.000001 0.000040 YES
Predicted change in Energy=-2.695932D-13
Optimization completed.
-- Stationary point found.
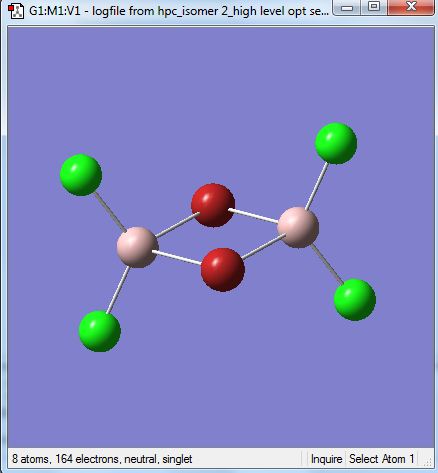
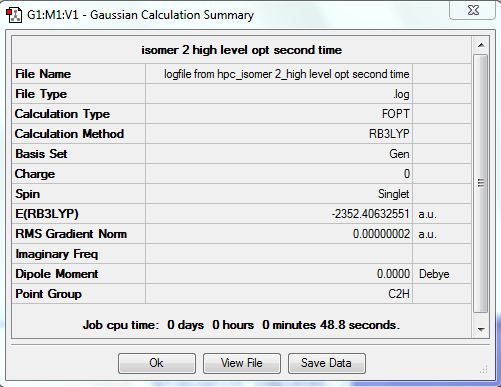
Isomer 2 [Cl2Al(µ-Br2)AlCl2]
The isomer is shown below and has symmetry D2h.
The first optimisation with the 3-21G basis set is linked here.DOI:10042/23997
The first time the higher level basis sets were used with the pseudo potentials the optimisation did not converge. The file is shown here DOI:10042/24001
The optimised file was re-run with the same pseudo potentials and it converged this time. The D-space link is here DOI:10042/24007 . The summary table is shown below.
It can be seen from the item table below that all forces and displacements have converged.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000000 0.000060 YES
RMS Displacement 0.000000 0.000040 YES
Predicted change in Energy=-3.636755D-14
Optimization completed.
-- Stationary point found.
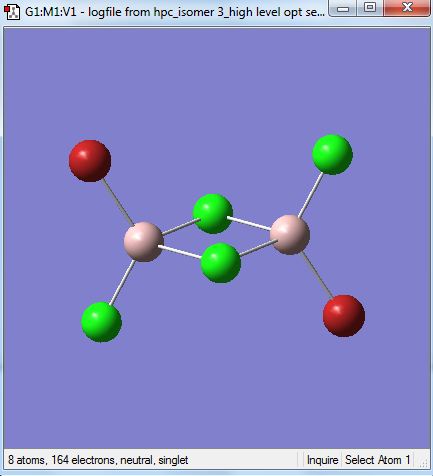
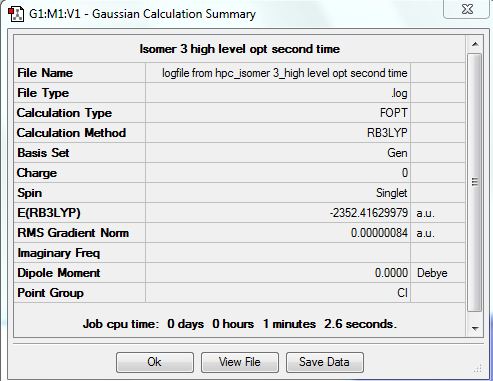
Isomer 3 [Trans-BrClAl(µ-Cl2)AlClBr]
The isomer is shown below and has symmetry C2h.
The first optimisation with the 3-21G basis set is linked here.DOI:10042/23998
The first time the higher level basis sets were used with the pseudo potentials the optimisation did not converge. The file is shown here DOI:10042/24003
The optimised file was re-run with the same pseudo potentials and it converged this time. The D-space link is here DOI:10042/24008 . The summary table is shown below.
The item table is shown below and shows that the forces and displacements have converged.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000019 0.000060 YES
RMS Displacement 0.000007 0.000040 YES
Predicted change in Energy=-3.736681D-11
Optimization completed.
-- Stationary point found.
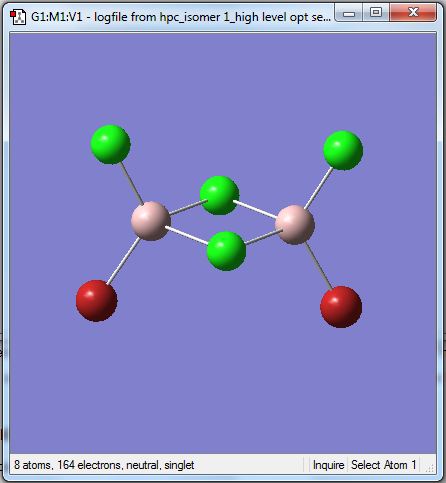
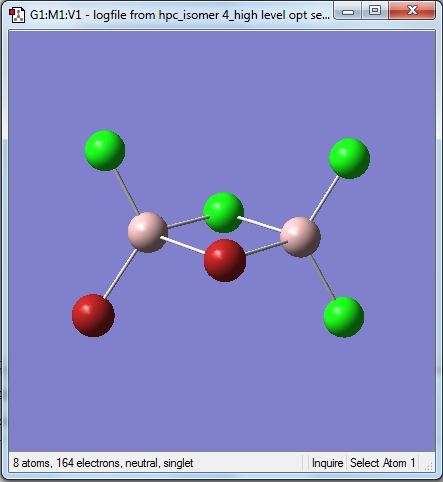
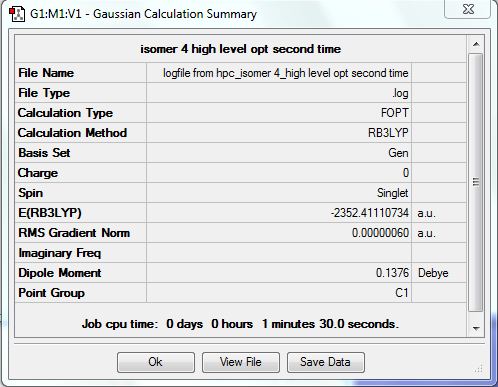
Isomer 4 [BrClAl(µ-Br,Cl)AlCl2]
The isomer is shown below and has symmetry C1.
The first optimisation with the 3-21G basis set is linked here.DOI:10042/23999
The first time the higher level basis sets were used with the pseudo potentials the optimisation did not converge. The file is shown here DOI:10042/24004
The optimised file was re-run with the same pseudo potentials and it converged this time. The D-space link is here DOI:10042/24009 . The summary table is shown below.
The item table is shown below and shows the convergence of the forces and displacements.
Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000011 0.000060 YES
RMS Displacement 0.000003 0.000040 YES
Predicted change in Energy=-6.253983D-12
Optimization completed.
-- Stationary point found.
Frequency calculations
Isomer 1 [Cis-BrClAl(µ-Cl2)AlClBr]
The D-Space link for the frequency analysis is here. DOI:10042/24016
The low frequencies are shown below. There are no negative values which proves that a minimum was found. The top row are within the correct range of +/-15cm-1
Full mass-weighted force constant matrix: Low frequencies --- -1.3336 -0.7717 0.0026 0.0034 0.0040 2.2145 Low frequencies --- 17.4967 51.1457 78.5265
The vibrational modes are shown below.
The computed IR spectrum is shown below.
Isomer 2 [Cl2Al(µ-Br2)AlCl2]
The D-Space link for the frequency analysis is here. DOI:10042/24018
The low frequencies are shown below. They confirm a minimum as there are no negative and they are in the correct range.
Low frequencies --- -0.8435 -0.0042 -0.0039 -0.0031 1.2999 1.3767 Low frequencies --- 16.0714 63.6245 86.1128
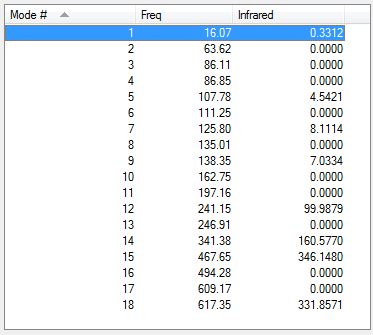
The vibrational frequencies are shown below.
The Ir spectrum computed from GaussView is shown below.
Isomer 3 [Trans-BrClAl(µ-Cl2)AlClBr]
The D-Space link for the frequency analysis is here. DOI:10042/24021
The low frequencies are shown below. There are no negative values which confirms that a minimum was found. The values are also in the correct range.
Low frequencies --- -2.4013 -1.6021 -0.6146 -0.0031 -0.0030 -0.0016 Low frequencies --- 18.1728 49.1591 72.8902
The vibrational frequencies are shown below.
The computed IR is shown below.
Isomer 4 [BrClAl(µ-Br,Cl)AlCl2]
The D-Space link for the frequency analysis is here. DOI:10042/24022
The low frequencies are shown below. It can be seen than there are no negative values which is proof that a minimum was found. They are also in the correct range.
Low frequencies --- -0.0502 0.0042 0.0043 0.0043 1.1119 1.8039 Low frequencies --- 16.9433 55.9191 80.0644
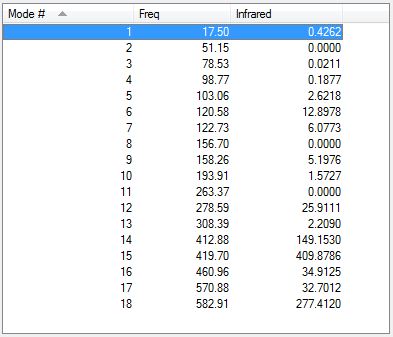
The vibrational modes are shown in the table below.
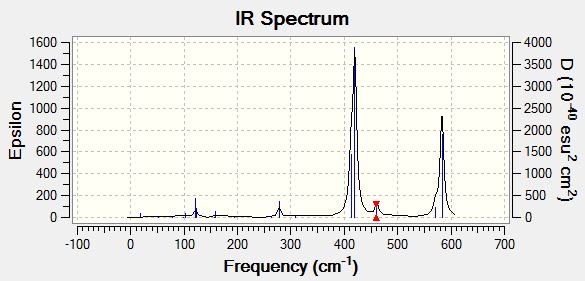
The IR computed from GaussView is shown below.
Discussion of frequency calculations
For each isomer the table of vibrational frequencies shows 18 different modes. This makes sense as each isomer has the same geometry so should have all the same stretches and bends. However none of the IR spectra show 18 peaks! The main reason for this is that not all the bands are experimentally active. Computationally we can calculate all possible modes but not all of these are IR active. For a band to be IR active there must be a change in the electric dipole moment associated with it.
A huge effect on whether a mode will be IR active or not is the symmetry of the molecule. Each of the four isomers has the same geometry and atoms but it is the placements of these atoms within the isomer which is important in determining symmetry. It can be seen from the computed IR spectra above that there is a clear trend between the level of symmetry of the isomers and the number of observed IR peaks. The higher the level of symmetry in the molecule the lower the number of IR active modes. The most unsymmetrical isomer [BrClAl(µ-Br,Cl)AlCl2] with symmetry group C1 shows the most IR active peaks by far. The more symmetrical [Cl2Al(µ-Br2)AlCl2] with point group D2H has less IR active modes. The cis and trans isomers of [BrClAl(µ-Cl2)AlClBr] have even less IR active modes due to their high level of symmetry. They have similar point groups of C2V (cis) and C2H (trans) and have almost identical IR spectra.
The cis and trans isomers provide the easiest way to visualise the effect symmetry has on dipole moment and therefore IR activity. This is because they have very similar structures and it is simple to see how the small change in atomic placement changes the dipole moment associated with certain modes. From the tabulated vibrational frequency data it can be seen from the infrared column (intensity) which peaks are the most IR active. Anything below around 30 is not significantly IR active. A mode that highlights nicely the effect of symmetry and atomic placement on IR activity is the symmetric stretch shown below.
| Vibrational Stretch (cm-1) | Animation | IR Active |
| [Cis-BrClAl(µ-Cl2)AlClBr] Symmetric Stretch at 461cm-1 |  |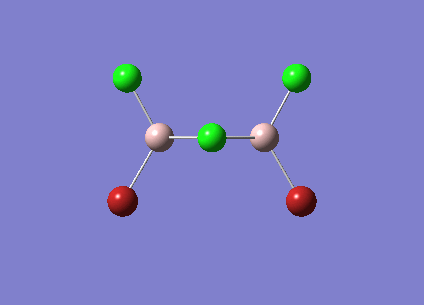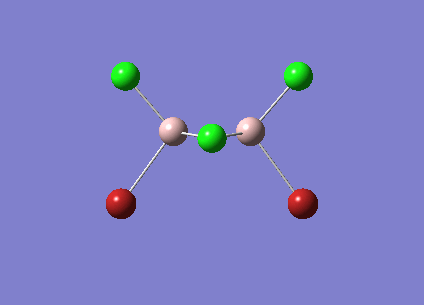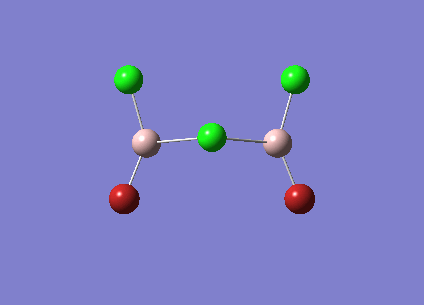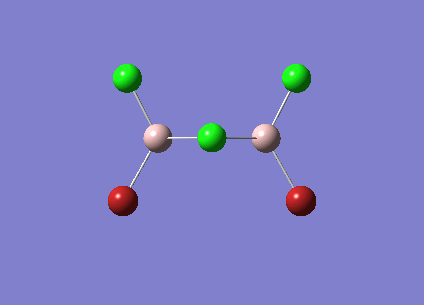
YES |
| [Trans-BrClAl(µ-Cl2)AlClBr] Symmetric Stretch at 459cm-1 |  |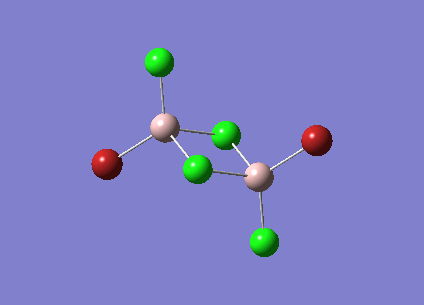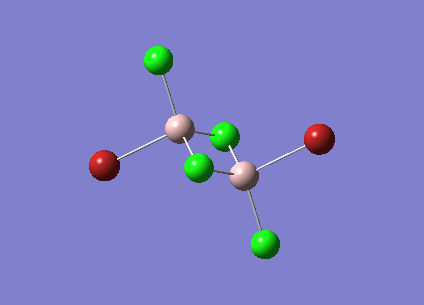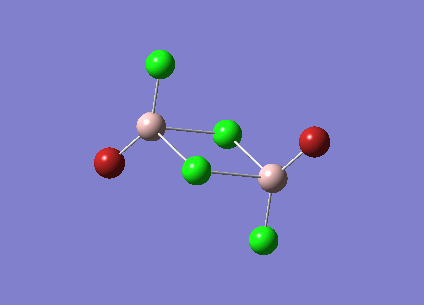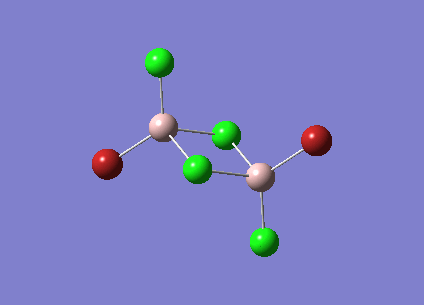
NO |
The symmetric stretches shown above are the equivalent modes for the cis and trans isomers and occur in the spectrum at very similar frequencies. The cis isomer stretch is IR active as there is a change in dipole moment as the stretch happens. The trans isomer however is not IR active as the dipole changes in the bonds are cancelled out due to the symmetry of the molecule. The dipole changes for the two Al-Br stretches cancel each other out as they are in opposite directions. This is also true of the Al-Cl bond stretches. As there is no overall dipole change the mode is not IR active. Therefore this peak does not show up in the IR spectrum for the trans isomer but does for the cis isomer.
The position of the Al-Br vibrational stretch in the IR spectra is affected strongly by the nature of the bond. The aluminium can bond to either a bridging bromine or a terminal bromine depending on which isomer we are looking at and this affects the stretching frequency. A tabulated comparison of Al-Br stretching modes in all four isomers is shown below.
| Vibrational Stretch (cm-1) | Animation |
| 420 |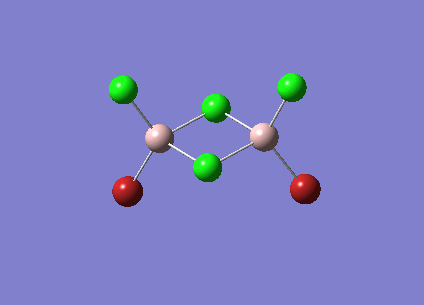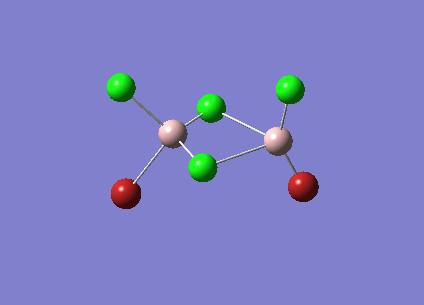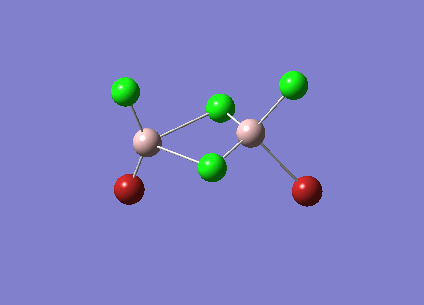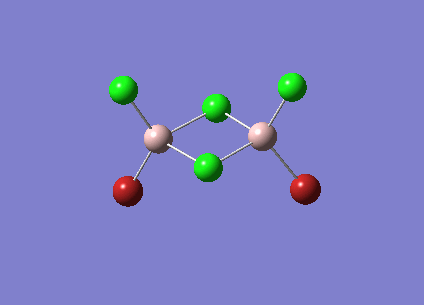 
|
| 247 | 
|
| 421 | 
|
| 424 | 
|
It can be seen above that the nature of the Al-Cl bonds, in terms of whether it is terminal or bridging, affects the stretching frequency significantly. The isomers with terminal Al-Cl bonds show stretches at around 420 cm-1. The isomer with no terminal bromine atoms shows no stretch here but does show one at 247 cm-1. This difference is due to the different strength of the terminal and bridging bonds. The frequency of a vibration depends on both the strength of the bond and the reduced mass. As the two atoms in the bond are identical the reduced mass is the same for both and bond strength must be the key factor. Stronger bonds have higher frequencies, as bond strength and frequency are directly proportional, which suggests that the terminal bond is stronger than the bridging bond.
Relative Energies
The energies of the four isomers have been computed and frequency calculations have confirmed that they all converged. This means that all four were at their optimum geometries. The energies for the four isomers are shown in the table below in atomic units, kJmol-1 and then relative to the lowest energy isomer which is [Trans-BrClAl(µ-Cl2)AlClBr].
| Isomer | Energy (a.u.) | Energy (kJmol-1) | Relative Energy (kJmol-1) |
| [Cis-BrClAl(µ-Cl2)AlClBr] | -2352.41627846 | -6176268.939 | 0.056 |
| [Cl2Al(µ-Br2)AlCl2] | -2352.40632551 | -6176242.808 | 26.187 |
| [Trans-BrClAl(µ-Cl2)AlClBr] | -2352.41629979 | -6176268.995 | 0.0 |
| [BrClAl(µ-Br,Cl)AlCl2] | -2352.41110734 | -6176255.363 | 13.632 |
It can be seen from the table of relative energies above that the position of the Bromine atoms within the isomers has an effect on their stability. More specifically it is the presence of bridging bromine atoms which affects the energies of the isomers. Each isomer has two halogens, either chlorine or bromine, bridging the two aluminium atoms together. These bridges occur due to the way that the two AlCl2Br monomers associate together. Aluminium is is group 3 of the periodic table and is electron deficient in AlCl2Br. The halogen atoms have lone pairs so are electron rich. The aluminium atom therefore acts as a lewis acid and accepts electron density from the lewis basic halogens to form bridges. The bridging of the different halogen atoms causes there to be different isomers.
There is a trend showing that as the number of bridging bromine atoms increases the isomers becomes less stable. Both [Cis-BrClAl(µ-Cl2)AlClBr] and [Trans-BrClAl(µ-Cl2)AlClBr] have no bridging bromines, only bridging chrorines. Both these isomers have very similar energies in relative terms. [BrClAl(µ-Br,Cl)AlCl2] has one bridging bromine and loses about 13kJmol-1 in energy. [Cl2Al(µ-Br2)AlCl2] has both bridging atoms as bromines and loses about 26kJmol-1 in energy. This shows that a loss of around 13kJmol-1 is incurred for every replacement of a chlorine bridging atom for a bromine atom.
It might be expected, due to the nature of the lewis basic donation of electron density from the halogen to the aluminium, that bridging bromines would actually stabalise the isomers more. Bromine is more electropositive than chlorine so should donate more electron density to the electron deficient aluminum, stabalising the complex more. This is the opposite to what is observed from the computational calculations. In fact the electron cloud on bromine is more diffuse than for chlorine so there is less effective orbital overlap with aluminium. This makes a weaker bond and helps to explain why the presence of bridging bromines decreases the stability.
Dissociation Energy of most stable isomer
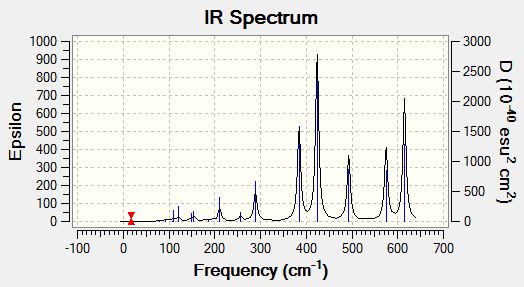
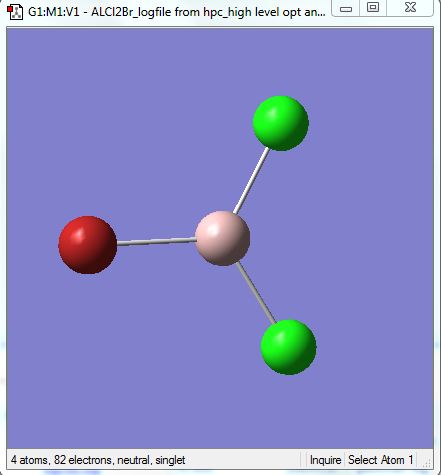
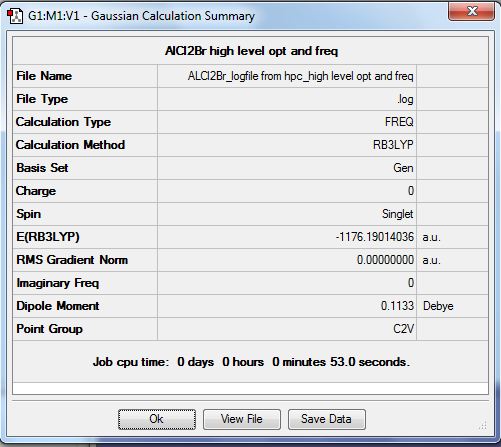
[Trans-BrClAl(µ-Cl2)AlClBr] is the lowest energy conformer so is the most likely to form. It forms from two AlCl2Br monomers. To calculate the dissociation energy of the lowest energy isomer the monomer moelcule must be optimised in order to obtain its energy. This was done using the B3LYP method. For the Aluminium and Chlorine atoms the basis set 6-31G(d,p) was used. The pseudo set LANL2DZdp was used for the bromine atoms. The optimisation and frequency analysis were run simultaneously and the results are shown below.
It can be seen from the RMS gradient above as well as the item table below that the optimisation converged and that a stationary point was found.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000000 0.000060 YES
RMS Displacement 0.000000 0.000040 YES
Predicted change in Energy=-6.376563D-16
Optimization completed.
-- Stationary point found.
The low frequencies below show that the stationary point found was a minimum as there are no negative values. The values are in the correct range of +/-15cm<sup-1.
Low frequencies --- -0.0037 -0.0036 -0.0032 1.8672 1.8720 3.5946 Low frequencies --- 120.7378 133.8465 185.7656
Two monomers are required to make one molecule of the [Trans-BrClAl(µ-Cl2)AlClBr]. Therefore to calculate the dissociation energy, the energy of the isomer must be take away from twice the energy of the monomer. This is shown below.
-1176.19014036 a.u. = -3088087.214 kJmol-1 (2x-3088087.214) - (-6176268.995) = 94.56796964 kJmol-1
The dissociation energy is positive which suggests that energy is required to form the two monomers from the isomer. This in turn suggests that the isomer is more stable than the two separate monomers. The formation of the isomer is enthalpically favoured.
Population Analysis of most stable isomer
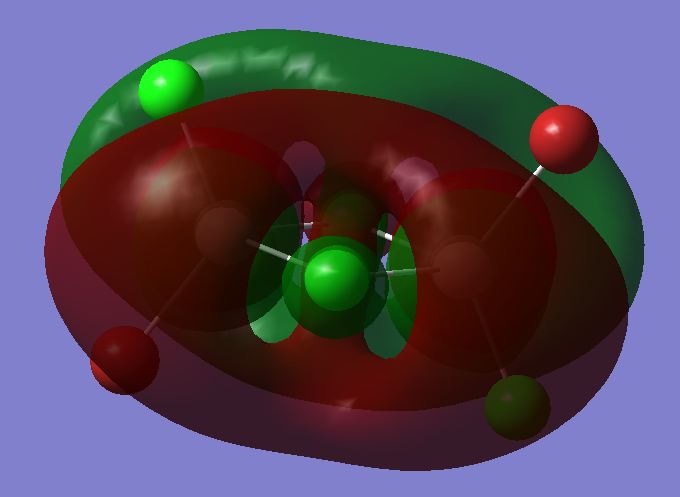
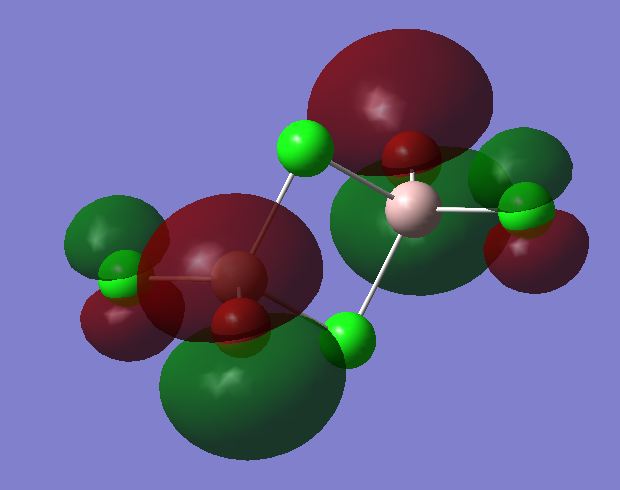
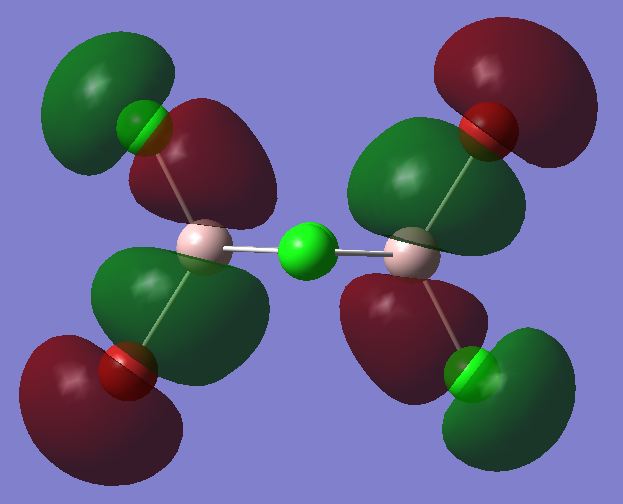
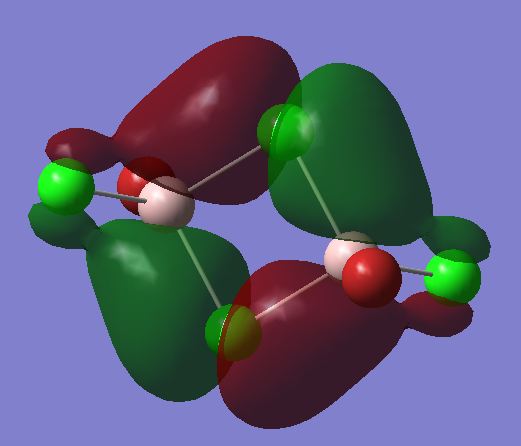
The checkpoint file from the optimisation of the most stable trans isomer was opened and a population analysis was run on it. This was done using the basis set LANL2DZ and pop=full as an additional key word. The competed file was deposited in D-Space DOI:10042/24044 . All the occupied non-core MOs were visualised. Core MOs are those made from core electron and non-core MOs are those made from valence electrons
| MO Number | MO Energy (a.u.) | Diagram | Description |
|---|---|---|---|
| 35 | 0.16208 |   |
This MO is highly anti-bonding and so has a high energy relative to the HOMO which has an energy of -0.33198 a.u. . There are strongly anti-bonding interactions between the aluminium atoms and the bridging chlorine atoms to make very delocalised MOs. There are several nodal points both on the atoms and between the atoms |
| 27 | 0.04991 |   |
This MO overall is slightly anti-bonding and sits just a few MOs above the HOMO. There are anti-bonding interactions through the bonds between the aluminium atoms and the bridging chlorine atoms. There also appears to be a very weak through space anti-bonding interaction between the two bridging chlorines. There are also non-bonding p atomic orbitals on the four terminal halides. Now there is antibonding there are nodal planes through the bonds and not through the atoms. These can be seen for the four Al-bridging Cl bonds. There are nodal planes on the aluminium atoms and the terminal halide atoms. |
| 21 | -0.33737 |  |
This is a non-bonding MO. There is no bonding or anti-bonding. The p atomic orbitals for the terminal bromines and chlorines can be seen. The bromine p orbitals can clearly be seen to be more diffuse than the chlorine p orbitals. There are nodal planes situated on the terminal halides and in plane with the terminal AL-X bonds. |
| 15 | -0.40629 |  |
This MO is occupied and sits quite far below the HOMO which has energy -0.33198 a.u. . The bonding interactions between the terminal halides and the aluminium can be seen. The atomic p orbitals have overlapped to give the MOs shown. Although the energy of this MO is quite low down the bonding interaction isn't huge and the MO is not massively delocalised. There are nodal planes on the aluminium atoms and the halide atoms. These are perpendicular to the bond. |
| 9 | -0.48868 |  |
This MO is strongly bonding and sits far below the HOMO. There are strongly bonding through-bond interactions between the AOs of aluminium and the AOs of the bridging chlorines. There are also bonding interactions between the aluminiums and the terminal chlorines. The charge on the terminal chlorines is localised but the charge across the central part of the molecule and the bridging chlorines is delocalised. There are nodal planes on the four chlorines and the two aluminiums. Four of these are in the plane of the termila bonds and two and perpendicular to the terminal bonds. |
References
- ↑ 1.0 1.1 1.2 W.M Haynes CRC handbook of Chemistry and Physics 2011 92nd Ed. 9-21 Cite error: Invalid
<ref>tag; name "Bonds" defined multiple times with different content - ↑ Blixt, Johan; Glaser, Julius; Mink, Janos; Persson, Ingmar; Persson, Per; Sandstroem, Magnus J. Am. Chem. Soc., vol. 117, 18, 1995 p. 5089 - 5104
- ↑ W.M Haynes CRC handbook of Chemistry and Physics 2011 92nd Ed. 26
- ↑ Yu. Kh. Shaulov; G. O. Shmyreva; V. S. Tubyanskaya, Zhurnal Fizicheskoi Khimii, 1966, 40,122-124