Rep:Mod:ja2209module3

Joshua Almond-Thynne: Year 3 Computational Labs - Module 3: Transition States and Reactivity

Introduction

The aims of this particular investigation is to gain a familiarity with the interface of Gaussian Transition State modelling, up until now (Module 1, Module 2) gaussview has been used to model compounds that are experimental obtainable and calculate their properties and then compare them to wet lab results. In this module Gaussview will be used to model products, reactants and most importantly transition states of certain reactions. This modelling allows us to gain insight into the mechanism of which a reaction may follow as well as key estimates of thermochemical data such as Free energies, Enthalpies, Activation energies and so on allowing us to look at whether selectivity may arise or whether a reaction may not even occur at all.

Unless stated otherwise stated all compounds modelled in this module where modelled in Gaussview 5.0 and calculation where run with their respective methods and basis sets via Gaussian 09W. If the calculation was deemed to be “large” the Gaussian input file (.gjf) was sent to the HPC server. If this was the case a D-space repository DOI will be supplied. If the calculation was run on the university issued laptop a .LOG file will be provided. If any other files are required for inspection please do not hesitate to ask via my email of ja2209@ic.ac.uk.

Also note that any conversions between Hartress and kcalmol^-1 or kJmol^-1 were made on the presumption: 1 Ha = 627.5 kcalmol^-1 and 1 kcalmol^-1= 4.2 kJmol^-1.

The Cope Rearrangement

The Mechanism For The Cope Rearrangement of 1,5-hexadiene

MO Summary of Cope Rearrangement

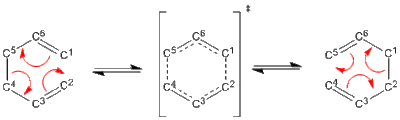
The cope rearrangement named after Arthur Cope is a [3,3] sigmatrophic rearrangement reaction for 1,5-hexadiene (and substituted forms) . It follows a pericyclic mechanism, which means three things:

• The electrons move in a concerted manner

• The electrons can move in either direction around the mechanism

• The reaction goes via a aromatic transition state

This reaction although concerted (which can be seen later in the report through imaginary frequency analysis) it is stated to go via a transition state which is equivalent to a di-radical structurally and energetically however this description is not quite correct and it is generally considered just a pictorial method to present the transition state. There are many various alterations of the Cope reaction such as the Aza-Cope or the Oxy-Cope. A particularly interesting case of the Cope rearrangement is that in the family of compounds called the Bullvalenes which the rearrangements causes its fluxional states. In occurs under mild conditions due to its symmetry allowed and complete suprafacial character allowing retention of any stereochemistry present.

Aims and Objectives

• To model and optimize all conformers of 1,5-hexadiene to find which one is the most stable and therefore the conformer in highest concentration.
  • Also a comparison between methods of optimising and there effect on energies and structure with a comparison between HF and DFT.

• Calculate vibrational and thermochemistry data for the most stable conformers and compare between conformers.
  • Also a comparison between methods for calculating vibrational and thermochemistry data between HF and DFT and DFT calculated at a theoretical 0K.

• Model both the chair and boat transition states in a number of ways and find out which is the most stable through vibrational analysis.

• Plot a reaction pathway diagram using IRS calculations giving an insight into the energy profile of a reaction.

• Final calculate the activation energies of the reaction through different transition states and compare them to literature value to see how accurate and useful transition state modelling can be.

Optimization of the Conformers of 1,5-hexadiene

All 10 Conformers of 1,5-hexadiene

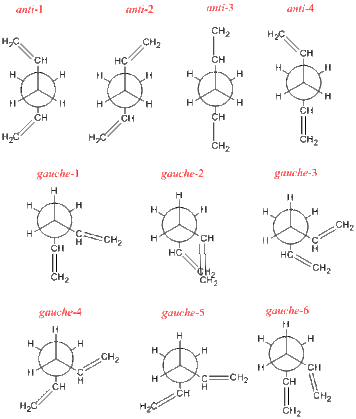
The first thing to not is 1,5-hexadiene exists in both anti and gauche conformers which correspond to how the CH=CH₂ arrange them selves around the central C-C bond. In ‘’anti’’ they are 90° to each other and in ‘’gauche’’ they lie 60° to each other. However both anti and gauche both has several sub conformers relying on the orientation of the C=C bond (or the dihedral angles adjacent of the C-C central bond and keeping the central dihedral fixed). All the conformers under investigation are seen in the picture to the right. (N.B. dihedral angles noted in the optimization table). Each conformer was then with optimized using a ‘’[HF/3-21G]’’ method and basis set. Their resulting energies in Hartrees (67.5kcalmol^-1) are in the table below aswell as there relative energies in kcalmol^-1 along with links to the jmol’s and their point group. The point group was found after optimization by forcing symmetry in Gaussian.

Conformer	Jmol	Total Energy (Ha)	Point Group	Relative Energy (kcalmol-1)	C3-C4-C5-C6 Dihedral Angle	C4-C3-C2-C1 Dihedral Angle	.LOG File
Anti 1		-231.69260	C2	0.04	115.5°	115.1°	.LOG
Anti 2		-231.69254	Ci	0.08	-114.7°	114.7°	.LOG
Anti 3		-231.68907	C2h	2.25	0.0°	0.0°	.LOG
Anti 4		-231.69097	C1	1.06	114.5°	0.2°	.LOG
Gauche 1		-231.68772	C2	3.10	-1.6°	-1.6°	.LOG
Gauche 2		-231.69167	C2	0.62	-124.0°	-124.0°	.LOG
Gauche 3		-231.69266	C1	0.00	-117.2°	120.9°	.LOG
Gauche 4		-231.69153	C2	0.71	109.4°	109.4°	.LOG
Gauche 5		-231.68962	C1	1.91	121.1°	14.2°	.LOG
Gauche 6		-231.68916	C1	2.20	1.0°	-139.1°	.LOG

Discussion of Stability

Looking in terms of sterics it would be assumed that the the anti would be preffered however from the table you can see that overall gauche is more stable. This however can be explained in terms of stereoelectronics. In the ‘’gauche’’ conformer there is alignment of there usually the stereochemistry of a conformer is effected by three things:

• Pauli Repulsion of bond electrons (prefers anti)

• H-H interactions when short are destabilising but and when long can be slightly stabilising (usually have a small favourability of gauche)

• Most importantly orbital interactions between various σ and σ*

These orbital interactions can actually be seen in the MO analysis, which I have run for the most stable conformer gauche-3 and the most stable anti; anti-1. From the NBO it can be seen there is more stabilisation of energy in this form of splitting in the gauche due to the σ_C-H-σ*_C-C having a larger stabilisation that that of σ_C-C-σ*_C-C.

ANTI-1

Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis Threshold for printing: 0.50 kcal/mol E(2) E(j)-E(i) F(i,j) Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u. =================================================================================================== 6. BD ( 1) C 4 - C 6 / 69. BD*( 1) C 9 - C 12 2.23 1.47 0.051 7. BD ( 1) C 6 - H 7 / 67. BD*( 1) C 9 - H 10 2.73 1.37 0.055 8. BD ( 1) C 6 - H 8 / 68. BD*( 1) C 9 - H 11 2.88 1.38 0.057 TOTAL STABILIZATION=7.84

GAUCHE-3

Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis Threshold for printing: 0.50 kcal/mol E(2) E(j)-E(i) F(i,j) Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u. =================================================================================================== 7. BD ( 1) C 6 - H 7 / 68. BD*( 1) C 9 - H 11 2.90 1.38 0.057 8. BD ( 1) C 6 - H 8 / 69. BD*( 1) C 9 - C 12 3.37 1.33 0.060 10. BD ( 1) C 9 - H 10 / 63. BD*( 1) C 4 - C 6 3.56 1.33 0.061 TOTAL STABILIZATION=9.38

The Homo of Gauche-3 showing "through space conjugation"

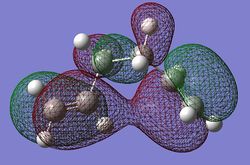
However this is not the only factor to take into consideration, the gauche conformers are more sterically strained therefore higher in energy, but at the same time an interesting MO was found in the gauche-3 conformer where the two terminal alkenes are aligned in the right way to have something i would describe as "through space conjugation" which can be seen in the diagram of the HOMO MO to the right of the page. As much analysis as I can do I cannot find a definitive answer to why something is more stable as such close energies it is a mixture of lots of effects canceling each other out or adding together but in this particular method the gauche is more stable.

Application of Full Electron Basis Set

Conformer	Jmol	Total Energy (Ha)	Point Group	Relative Energy (kcalmol-1)	C3-C4-C5-C6 Dihedral Angle	C4-C3-C2-C1 Dihedral Angle	.LOG File
Anti 1		-234.61779	C2	0.00	115.5°	115.1°	.LOG
Anti 2		-234.61170	Ci	3.82	-114.7°	114.7°	.LOG
Gauche 3		-234.61133	C1	4.05	-119.4°	122.1°	.LOG

The 3 most stable and closest in energy conformers where taken for further optimization by a full electron basis set which in theory will give a more accurate energy and structure.

From the application of [DFT/6-31G(d)] it can be seen that the expected result is shown where the anti-1/2 are now more stable than the gauche-3. This is due to the fact the full electron basis set is weighted slightly difference or the new slightly altered structure has a tiny amount more/less steric strain. A definitive reason will probably not be able to find but that is why you cant compare energies between basis sets/methods. With energies this close it could be one of a thousand reasons why the anti in this case is slightly more favorable than gauche.

Structural Comparison between Basis Sets

Gauche-3 was chosen for structural comparison due to the least symmetry in the conformer meaning it may be more likely to be effected.

The energies have shifted but the effect of different basis sets on structure is very small seen by the tabulated structure data for gauche-3 with very little difference coming from bond length/angle or dihedral angles. This shows that the structure does not change in a compound but the energies might drastically. This effect on structural is completely reliant on the way a particular method works on even its convergence criteria. But you can see from the comparison below a very small effect on structure is seen with the biggest effect being the dihedral angles.

Method	C1-C2 Length	C2-C3 Length	C3-C4 Length	C4-C5 Length	C5-C6 Length	C1-C2-C3 Angle	C2-C3-C4 Angle	C3-C4-C5 Angle	C4-C5-C6 Angle	C4-C3-C2-C1 Dihedral Angle	C2-C3-C4-C5 Dihedral Angle	C3-C4-C5-C6 Dihedral Angle
HF	1.32Å	1.51Å	1.55Å	1.51Å	1.32Å	124.5°	111.8°	111.9°	125.0°	120.9°	67.7°	-117.2°
DFT	1.33Å	1.50Å	1.55Å	1.50Å	1.33Å	124.9°	113.5°	113.5°	125.5°	122.1°	66.3°	-119.4°

Vibrational and Thermochemistry Analysis

The key points to make about the vibrational analysis is that none of the conformers showed no large negative frequencies showing they are indeed minimas in energy (rather than a non-minima i.e Transition state which shows large negative frequencies) and the differences in the C=C stretches of the compounds. All having similar values the anti' conformers have a smaller intensity for the symmetric C=C stretch than the gauche due to there increased symmetry meaning there there is less of a dipole moment change and therefore less IR active. Whereas the gauche both stretches have identical intensities because they both change the dipole moment in the same way.

A COMPARISON TO LITERATURE

Mode	Anti 1	Anti 2	Gauche 3
Symmetric C=C Frequency (cm-1)	1731.96	1730.95	1731.86
Symmetric C=C Intensity	4.73	0.00	6.89
Asymmetric C=C Frequency (cm-1)	1734.86	1734.95	1732.98
Asymmetric C=C Intensity	13.55	18.1624	6.89
Vibrational Spectra
.LOG FILE	.LOG	.LOG	.LOG

Thermochemistry of the Conformers

Anti 2 at 298K DFT Sum of electronic and zero-point Energies= -234.469218 Sum of electronic and thermal Energies= -234.461861 Sum of electronic and thermal Enthalpies= -234.460916 Sum of electronic and thermal Free Energies= -234.500832 Anti 2 at 298K HF Sum of electronic and zero-point Energies= -231.539540 Sum of electronic and thermal Energies= -231.532566 Sum of electronic and thermal Enthalpies= -231.531622 Sum of electronic and thermal Free Energies= -231.570915

Both methods give similar data to that of the energies of the optimized structure with similar differences in zero point and thermal values, In this case for the sake of accuracy I will continue to use DFT full electron basis set methods due to the fact in theory I will get more accurate results.

Anti 2 at 298K DFT Sum of electronic and zero-point Energies= -234.469218 Sum of electronic and thermal Energies= -234.461861 Sum of electronic and thermal Enthalpies= -234.460916 Sum of electronic and thermal Free Energies= -234.500832 Anti 2 at 0.0001K DFT (To prevent refusal of calculation) Sum of electronic and zero-point Energies= -234.468781 Sum of electronic and thermal Energies= -234.468781 Sum of electronic and thermal Enthalpies= -234.468781 Sum of electronic and thermal Free Energies= -234.468781

As you can see there is little difference between running the vibrational calculations at 298K and 0K with the value of sum of electronic and zero-point energies ≈0.005a.u.(≈3 kcalmol-1) however the complication of sending off the method for analysis with its more complex input files and larger CPU time I will continue to use the standard running of vibrational data at 298K for the sake of time. The other point of interest is for all 4 values run at 0K they are equal, This is a trivial but important point to make in the sense at 0K there is technically no thermal energies/enthalpies/free energies so all values should be the same which shows the calculation was successful. A possible investigation of the effects of temperature on the thermochemistry values would be to run the calculation at various temperatures and plot each of the 4 values against temperature. The calculation was run at 0K by adding the keyword Freq=ReadIsotopes with the additional data at the end of the .gjf provided in the table to the left.

0.00001 1.0 12.0 1.0 1.0 12.0 1.0 12.0 1.0 1.0 12.0 1.0 1.0 12.0 1.0 12.0 1.0 1.0

Anti 1 at 298K DFT Sum of electronic and zero-point Energies= -234.469298 Sum of electronic and thermal Energies= -234.461966 Sum of electronic and thermal Enthalpies= -234.461022 Sum of electronic and thermal Free Energies= -234.500862 Anti 2 at 298K DFT Sum of electronic and zero-point Energies= -234.469218 Sum of electronic and thermal Energies= -234.461861 Sum of electronic and thermal Enthalpies= -234.460916 Sum of electronic and thermal Free Energies= -234.500832 Gauche 3 at 298K DFT Sum of electronic and zero-point Energies= -234.468693 Sum of electronic and thermal Energies= -234.461464 Sum of electronic and thermal Enthalpies= -234.460520 Sum of electronic and thermal Free Energies= -234.500105

From the three difference conformers it can be seen the sum of electronic energies and zero point energies are very close in size with a difference between all three being ≈0.0006a.u.(≈0.3 kcalmol1) with the lowest in energy being the anti-1 and the highest being gauche-3. with all the thermal values varying to a similar amount in all the conformers. An additional investigation would be to look at the relative st abilities at different tempertautes to see if all the conormers follow the same trend of calculated thermochemistry values at different temperatures or see if one particular isomer becomes more favorable with increased heat.

Optimization of the Transition States

Chair Transition State	Boat Transition State

The Cope-Rearrangement goes via an aromatic transition state which can either be a Chair or Boat Cyclohexane ring. In the following section several approaches to modelling a transition state will be attempted with a comparison between the structural outcomes / their relative energies. The Chair transition state will be modelled using a [HF 3-12G] method and basis set with minimizing to a TS(Berny). Using a few different methods of allowing control over the optimization by freezing certain co-ordinates. With the second method the Boat will be optimized using the same method and basis set but minimizing to a TS(QST2) method where you model the reactant and the product and it "extrapolates" between the two to make a transition state.

The Chair Transition State

A allyl fragment was optimized using a [HF 3-21G] method and was copied into a new molecule group window twice. The two fragments were orientated to resemble the Chair structure. The terminal carbon distance was set to 2.20Å and the two methods (A) and (B) were run. In A a force constant matrix (Hessian Matrix) was calculated during each optimization iteration and this was used to find where the compound is on the potential energy surface. In B the terminal carbons co-ordinates were frozen and a minimization is run to "relax" the rest of the molecule, this is then re optimized to a TS(Berny) using a derivative of the frozen co-ordinates to calculated the force constant of the essential bond in the transition state. All the key information is provided below:

Information	Method A	Method B
Energy (Ha)	-231.61932	-231.61932
Terminal Carbon Distance (Å)	2.02	2.02
Absorption Frequency (cm-1)	-817.96	-817.96
Absorption Intensity	5.8504	5.8504
Animation of Vibrational Mode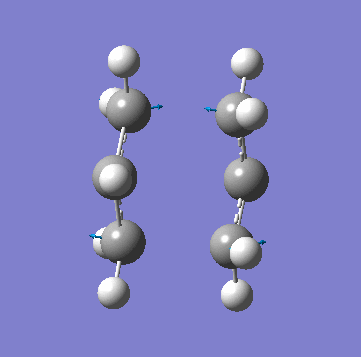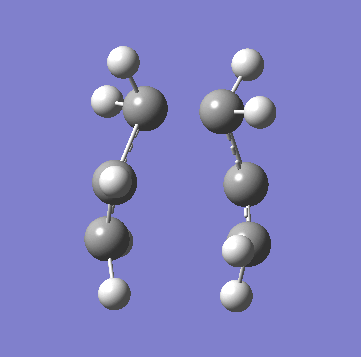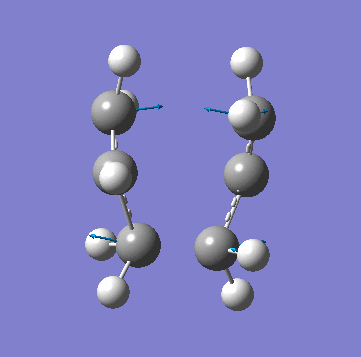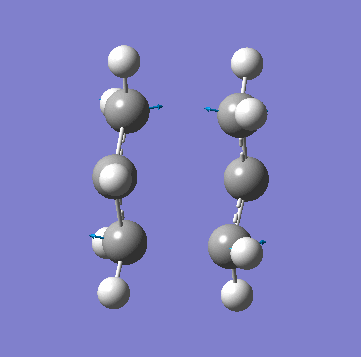
Jmol Link
.LOG File	.LOG	.STEP1LOG .STEP2LOG

As you can see from the table above both methods give the exact same data. This is due to the fact in this relatively simple transition state my guess of the structure used in method A is quite reliable. Method B bascially breaks up method A into two parts where you make your structure and freeze the atoms you know are involved in the transition state then "clean" the remainder of the structure to a minimum. Stage 2 then optimizes the derivative of the transition state essential bond to find where it is at its maxima and calculated the frequency from there. In method A the initial guess is reliable is optimized and at each iteration the force constant matrix is calculated which is used to predict the PES. The most important thing to get from this comparison is that method A is suitable for simple transition states or ones that you know the structure of but it is a lot more reliable to use method B is you are unsure.

The Boat Transition State

QTS2 Method requires products and reactants separately. The method then extrapolates from one to the other to form an idea of the transition state. The conformers where drawn and the atoms were labelled in the following way sticking to the script of the module 3 wiki page. The optimization was run and the data of interest if tabulated below.

A note be make is the products were drawn in gaussview but the geometries were changed in promote the "finding" of the Boat transition state, without this geometric manipulation the Boat could not be found in the optimization. The labeled original and manipulated products can be seen in the table below also:

Conformer	Product	Reactant
Original Geometry
Modified Geometry
(N.B.- Pictures taken straight from module 3 wiki pages)
Boat Transition State Calculated Data
Energy (Ha)	-231.60280
Terminal Carbon Distance (Å)	2.14
Absorption Frequency (cm-1)	-840.13
Absorption Intensity	1.6100
Jmol Link
Absorption Animation
.LOG	.LOG

The key points of interest for the table are:

• The final energy of -231.60280a.u. which gives a relative energy in comparison to the Chair TS^‡ to be +10.366 kcalmol^-1 which fits with the literature and general knowledge that Chair is more stable than Boat.
• There is one negative frequency showing that this is in fact a non-minima in energy and actually a maxima with the negative absorption being at -840.13 which when the animation is watched corresponds the the Cope Rearrangement.
• The terminal carbon distance is 2.14Å which is longer than that of the Chair transition state which is 2.02Å which could to why the Boat is a less preferred pathway for the reaction to occur.

IRC Calculations

Calculating FC Once vs. Calculating FC Always

When running a IRC calculation it is possible to calculate force constants once at the beginning of the optimization and "guess" them for the resulting structure which significantly decreases CPU time, However an option to calculate force constants at every iteration in theory would give a lot more accurate results. In this section both methods were run for the Chair Transition state with the data tabulated below:

Data	Force Constant Calculated Once	Force Constant Calculated Always
Final Energy (Ha)	-231.686832	-231.691322
Final RMS Gradient (Ha)	0.00103902	0.00001769
Number of Iterations	25	47
Energy Profile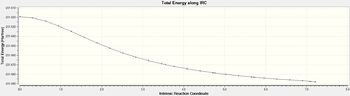
Gradient Profile
Corresponding Conformer	Gauche-2	Gauche-2
Difference In Energy From Conformer (kcalmol-1)	+3.03	+0.22
DOI	.LOG	DOI:10042/to-12342

In the data seen above it can be seen that calculating force constants always gives a more accurate for the two main reasons of it leads to more iterations and therefore more point of data to map the energy profile but also that the final structure found is a lot closer in energy to the conformer optimized in the first section of this report. This shows for the comparison between Chair and Boat will be made with using the calcall function of calculating force constants always.

Chair vs. Boat IRC Calculations

The optimized structures of Chair and Boat ([HF 3-21G]) were then sent for IRC analysis with the following method:

# irc=(forward,maxpoints=50,calcall) rhf/3-21g geom=connectivity

All output daya is tabulated below:

Data	Chair Transition State	Boat Transition State
Final Energy (Ha)	-231.619322	-231.692637
Final RMS Gradient	0.00001769	0.00004175
Number of Iterations	47	75
Energy Profile
Gradient Profile
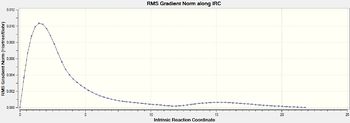Corresponding Conformer	Gauche-2	Gauche-3
Difference In Energy From Conformer (kcalmol-1)	+0.22	+0.01
Optimized Structure jmol
DOI	DOI:10042/to-12342	DOI:10042/to-12341

The data shows that both TS^‡ follow very similar pathways with the the energy starting at a minima then increasing to a maximum of the transition state and then relax back down to the minima. A further calculation that could be run was the reaction in both directions and then both the IRC calculation plotted on the same graph to give a comparative energy profile. However I believe this not to be necessary due to the fact the IRC should be close to symmetrical going forwards and backwards due to there being no chemical change in the molecule and it is a know fact from the previous optimization that the Boat Transition state is the one with a higher energy Therefore higher energy barrier.

Reaction Thermochemistry

The optmized TS^‡ was taken and further optimized using [DFT (6-31G(d)] method and basis set which is a full electron "more accurate" approach, This was then sent for frequency analysis to gain the thermochemistry data for the TS^‡. This data is used because it is a more indepth method of calculation and a table with all important points are tabulated below. Also DOI links to the D-Space Repository are provided below:

(Chair: Optimization;DOI:10042/to-12451 Frequency;DOI:10042/to-12453 )/(Boat: Optimization;DOI:10042/to-12452 Frequency;DOI:10042/to-12454 )

Transition State	Point Group	Sum of Electronic and Zero Point Energies (a.u.)	Sum of Electronic and Thermal Energies (a.u.)	Sum of Electronic and Thermal Enthalpies (a.u.)	Sum of Electronic and Thermal Free Energies (a.u.)	Activation at 298K (kcalmol-1)x	Activation at 0K (kcalmol-1)xx	Literature Activation Energy (kcalmol-1)
Chair	C2h	-234.414930	-234.409009	-234.408065	-234.443815	33.23	34.12	33.5±0.5
Boat	C2v	-234.398511	-234.392584	-234.391640	-234.427337	43.54	44.42	44.7±2.0

^xActivation at 298K has been calculated by finding the differences of Sum of Electronic and Thermal Energies of the lowest energy conformer for this method (anti-1) and that of the transition state (-234.461966 a.u.)

^xxActivation at 0K has been calculated by finding the differences of Sum of Electronic and Zero-Point Energies of the lowest energy conformer for this method (anti-1) and that of the transition state (-234.469298 a.u.)

From the stable above it can be seen that the activation energies found are very close to that of the literature values which shows in this case this method has been reasonable accurate. Other points of interest is that the Chair has a lower activation energy than the Boat conformer

Conclusion to The Cope Rearrangement

From the investigation it can be said that the methods even though still relatively crude to those currently used in research have given quite accurate results when comparing to literature for the activation energies aswell as confirming the preference of the Chair TS^‡ over the Boat TS^‡. From the thermochemical data obtained it has also confirmed the reaction does not require a lot of external heat to start the reaction either forwards or backwards and explains why in some cases this rearrangement can cause fluxionality in NMR. It has also highlighted the advantages and disadvantages of certain methods in TS^‡ modelling covering quite a few methods. From here the investigation continues onto looking at why certain TS^‡ are more stable than others along with MO analysis or certains species.

Diels-Alder Reaction

Introduction

Reaction Scheme with cis-butadiene and ethene

In this particular investigation there will be more modeling of transition states but with a focus on molecular orbital interactions meaning certain TS^‡ are favoured over others. In this investigation I will be looking at two Diels-Alder Reactions. Firstly the simplest and probably most famous; the reaction between cis-butadiene and ethene to produce a cyclohexene ring. Secondly the reaction between maleic anhydride and 1,3-cyclohexadiene where the endo selection rule is seen in full effect. The endo-selection rule is seen throughout many diels alder reactions. Due to the stability of the products made in most diels-alder reactions it usually follows a kinetic pathway which means it goes via the lowest energy TS, Which in a lot of cases is the endo. This is due to stabilizing frontier orbital interactions and that is the main focus in the project.

cis-butadiene with ethene

In this particular reaction there is no case of endo or exo selection due to the simplicity of the reaction, In this investigation there will be a TS^‡ will be modelled with the HOMO and the LUMO being presented in this report with discussion on what they mean and how the reaction works.

cis-butadiene

cis-butadiene was optimized initially with the semi empirical method AM1 with the data tabulated below:

Energy (Ha)	0.04879720	RMS Gradient (Ha)	0.00004491
HOMO		LUMO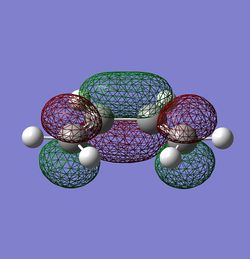
HOMO Symmetry	a	LUMO Symmetry	s
C-C Bond Length (Å)	1.450	C=C Bond Length (Å)	1.335
Lit C-C Bond Length (Å)	1.470	Lit C=C Bond Length (Å)	1.340
Jmol Link		.LOG File	.LOG.

This data shows nothing of real interest but will be used in a comparison in the TS^‡ modelling in the next section:

Transition State Modeling

The transition state was optimized by both AM1 and DFT ([DFT 6-31G(d)]) and the data is tabulated below:

Data	AM1	DFT
Energy (Ha)	0.111655	-234.54389
RMS Grad (Ha)	0.000031	0.00000041
HOMO	Symmetry a	Symmetry a
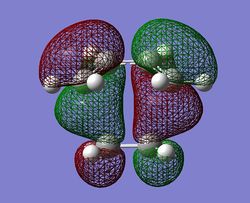LUMO	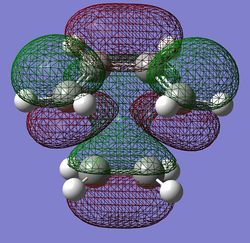Symmetry s	Symmetry s
C-C Bond Length is butadiene fragment Å	1.40	1.41
C=C Bond Length is butadiene fragment Å	1.38	1.38
Terminal Carbon Distance Å	2.12	2.27
Negative Absorption Frequency (cm-1)	-955.80	-524.99
Negative Absorption Intensity	5.6245	5.7947
Jmol
DOI/.LOG	.LOG	DOI:10042/to-12515

The main points of interest from the table above are the following:

• The C-C bond lengths decrease from the stand alone cis-butadiene which shows the process of becoming the shorter stronger C=C bond length (difference of -0.05Å)
• In the same way the C=C bond length has increases showing that the C=C bond have started there transformation into the C-C bond ins the final product (difference of -0.45Å)
• This change in bond length occurs in both methods and comparing between the two there are two major points to make:
  • The Terminal C-C bond length has increased in the DFT method by 0.15Å.
  • The imaginary frequency has changed drastically between the two methods.
    • The reason between these values is because when estimating the PES there are differences in energy and geometry, these meant the gradient around the maxima which is the TS^‡ is different. The frequency relies on the second derivative of the curve and if the gradient is different around this maxima it will have a large effect on the frequency. This is the real reason why you cannot compare energies of methods and imaginary frequencies.
• However looking at the animation of the imaginary frequency (seen by clicking the link in the table) it shows the bond formation/breaking is synchronous which is to be expected from the pericylic diels-alder reaction where one of the definitions is that the whole process is concerted.
• Ψ(TS^‡, HOMO)= Ψ(cis-butadiene, HOMO)+ Ψ(ethene, LUMO)
• Ψ(TS^‡, LUMO)= Ψ(cis-butadiene, LUMO)+ Ψ(ethene, HOMO)
  • The reaction is allowed because you have the HOMO of the cis-butadiene mixing with the LUMO of the ethylene (π* orbital) which are both anti-symmetric which go to form the anti-symmetric HOMO of the TS^‡.
  • The HOMO is made up of the π-orbital of the cis-butadiene combining witht the π* orbital of ethene which corresponds to the π-bond breaking in the cis-butadiene and ethylene to form new sigma bonds.

1-3-Cyclohexadiene Reaction with Maleic Anhydride

Overview

Reaction Scheme with 1,3-cylcohexadiene and maleic anhydride

In this particular reaction there is a case of endo vs. exo In this investigation I will be comparing different methods of optimization as well as a full MO comparison between isomers and methods highlighting key interactions. After this I will attempt to create a energy profile for the reaction using more advanced IRC calculations compared to ones seen earlier in the report and use these to explain the endo selection rule with the stabilites of the TS^‡ and the Products.

endo vs. exo Optimizations

The first step in this experiment is to optimize the endo and exo to there respective TS^‡ and compare the two methods as well as the two isomers. All data is tabulated below:

Data	Exo		Endo
Method	AM1	DFT	AM1	DFT
Energy (Ha)	-0.050420	-612.679310	-0.051504	-612.683397
Reactive Carbon Distance Å	2.17	2.29	2.16	2.27
Negative Absorption Frequency (cm-1)	-812.38	-448.50	-806.37	-446.96
Negative Absorption Intensity	96.8772	5.5115	71.5669	1.4432
Jmol
DOI/.LOG	.LOG	DOI:10042/to-12464	N/Ax	DOI:10042/to-12463

^x .LOG file too big to upload will provide under request.

From the data it can be seen:

• The endo TS^‡ is more stable than the exo showing this would be the preferred kinetic pathway.
• The frequencies/terminal carbon bond lengths change between methods but between isomers these values are very similar.
• A discussion of stability caused by molecular orbitals will be seen in the next section.

endo vs. exo Molecular Orbital Diagrams

The Molecular Orbitals were visualized using both HF and DFT methods, will a comparison between isomers for each below:

AM1 Calculated MOs

Transition State	LUMO+2	LUMO+1	LUMO	HOMO	HOMO-1	Exo-Energy Profile	Endo-Energy Profile
Endo-Transition State
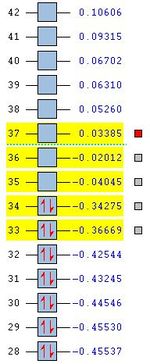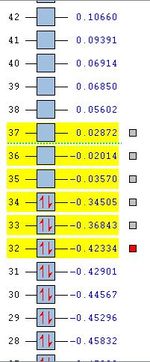Exo-Transition State

Between the two isomers the following points should be noted:

• The Ψ(endo, LUMO+1)=Ψ(Maleic Anhydride, HOMO)+Ψ(1-3,Cylcohexadiene, LUMO) is the major secondary orbital interaction which is usually stated as the reasons for the endo TS^‡ however it is seen to be in the LUMO+1. This would indicate it would not have a large effect. It is also seen in the exo to a lesser extent due to increased distance between the two MO's mixing.
  • There are two possibilities for this MO to be higher in energy than expected, One is based on the fact that in this particular method the MO's are just in the wrong order and it is in fact lower in energy than the LUMO/HOMO and it is the major stabilizing effect seen in the experimental and could be altered using a different method.
  • The second idea is slightly more strange, I have the hypothesis that when looking at the secondary orbital overlap it can been sent he the MO is heavily weighted to one side of the molecule in the endo, this would imply that in theory it could be stabilized by a polar solvent (a common solvent for Diels-Alder reactions) therefore a polar solvent could lower this energies orbital to become a occupied one and it causes the stability seen. All the calculation run in this project have been run in the gas phase to reduce CPU time / not have the error of a poor solvent model. A further investigation could be to run the optimizations again in a polar solvent and see if it has an effect on the MO's energies.
  • However for this particular method the endo is still preffered therefore it can be said that there are other factors dominating the stability between the two TS^‡ such as additional splitting or sterics Full NBO analysis could be run to find this out. A full steric effect showing favor towards the endo product can be seen in my first Module 1 showing that in that case it was Torsion around the C=C bonds deciding the stability.
• The Final point to make is that the HOMO in both the exo and the endo correspond the the making of the new sigma bonds formed in the reaction which shows the reaction is going as expected and is symmetrically allowed (Ψ(endo, HOMO) = Ψ(Maleic Anhydride, LUMO) + Ψ(1,3-Cyclohexadiene, HOMO) which are both anti-symmetric)

6-31G(d) Calculated MOs

Transition State	LUMO+2	LUMO+1	LUMO	HOMO	HOMO-1
Endo-Transition State
Exo-Transition State

The comparison between basis sets show no real difference in shape between MO's. The only thing of interest to mention is that some of the degnerate MO's swap in order in the basis set. This could be due to many factors but would have no real effect on the overall energies of the two isomers. (example of HOMO/HOMO-1 in the exo TS^‡) This is another example of the fact that you cannot compare ENERGIES between methods and basis sets however there is little difference in structure and in this case molecular orbitals.

Energy Profile

IRC was run for both the endo and exo transistion states at 100 iterations, force constants calculated always under semi empirical AM1 with the following method:

# irc=(maxpoints=100,calcall) ram1 geom=connectivity

The Data with excel diagram showing both energy diagrams on one graph (made in Excel) is shown below is presented below:

Data	Endo	Exo	Final Energy Pathway Diagram
Final Energy (Ha)	-0.094720	-0.095779	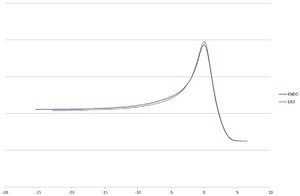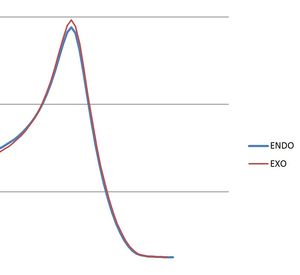Energy Diagram Pathway Made on Excel For Both Endo and Exo TS‡/products Zoomed In Highlighting TS‡ area of reaction pathway
Optimized DFT Final Energy (Ha)	-613.99109069	-613.99109076
Final RMS Gradient (Ha)	0.00005	0.00001769
Number of Iterations	124	110
Energy Profile
Gradient Profile
Pathway Animation
Activation Energy (kcalmol-1)	21.12	28.46
DOI	DOI:10042/to-12494	DOI:10042/to-12495

From the IRC calculations it can be seen both reactions go via a very similar pathway seen by the animations with the only difference being seen int he excel graph with both pathways plotted with the endo being slightly lower in energy than that of the exo ≈10kcalmol^-1. Therefore again confirming the endo would be preferred if the reaction ran via a kinetic pathway. However a slightly unexpected result is that of the products. The two final energies of the IRC calculations are only different by 0.6kcalmol^-1 favouring the exo.This was confirmed by a separate [DFT 6-31G(d)] optimization of the products (endo:DOI:10042/to-12513 , exo:DOI:10042/to-12514 ) which gave the energies also noted in the table with a difference of 0.00004kcalmol^-1 This shows that even under thermodynamic control both products would form a nearly equal mixture of both products. Other Points of Interest Include:

• Activations for the endo and the exo pathway differs by 7.34 kcalmol^-1 favouring the endo product.
• The gradient of the IRC calculations drops to zero confirming it is defiantly a maxima in energy.

Discussion of Diels-Alder Reaction

During this investigation the visualisation of MO's has confirmed several pieces of information seen from the experimental / theory, including the bond formation of the two new two σ-bonds is synchronous and the reaction is symmetry allowed. Other pieces of data for maleic anhydride is obtained is the confirmation of the endo TS^‡ preferred over the exo even though this particular modelling shows its not due to secondary overlap which is believed to be the cause, however further modelling may change the results. And finally the calculation showing the exo/endo products are equal in energy which is not the usual scenario where the exo is seen as the thermodynamic product in many cases of diels-alder reactions. However further investigation into solvent effects on the products could change this as it may be a case that one products is more stable than the other in a polar environment which is the the biggest factor neglected from all the calculations in this module. However if solvent was taken into account it would not be 100% reliable and CPU time on all calculations would increase drastically. However overall a good understanding has been found in modelling transition states aswell as some very reliable data obtaining giving a key insight into some overlooking very important reactions.

Please note I did attempt a mini-project of the experiment of Cyclopentadiene Dimerisation seen in Module 1 However with time constraints and trouble optimising to a TS(Berny) I was not possible to gain any usable data.