Rep:Mod:ja2209module2
Joshua Almond-Thynne: Year 3 Computational Labs - Module 2: Bonding (Ab initio and Density Functional Molecular Orbital)
Introduction
In this module of computational chemistry the focus is on quantum mechanic based method. Thee will be used to gain insight into the structures and reactivities of certain compounds and then compared to experimentally gained data to find how accurate and which situations it is appropriate to use such methods. Comparisons to other methods such as LCAO or pseudo-poteintial like basis sets will also be made highlighting there pros and cons. Unless otherwise stated all calculations were made through Gaussview 5.0 and run through Gaussian 09W either on the university provided laptop or via the high performance computer (HPC) server.
Computational Analysis of the Molecular Orbitals of BH3
Aims and Objectives
This initial project is the investigate the accuracy and usefulness for quantitative computational MO theory. It will start with the optimization of BH3 to show and explain the optimization process. From this optimized structure the vibrational dat of the compound will be calculated to compare calculated frequencies and the experimental. Followed by MO and NBO analysis to show how it can give an insight into the reactivity of a compound with looking at which atomic orbitals make up the HOMO, LUMO allowing an insight into where the chemical reactivity occurs. With a comparison between with this method and the LCAO method to see the similarity between the two methods.
Optimization
BH3 was drawn in Gaussview 5.0 with all B-H lengths of 1.50Å, this was optimized using [DFT: B3LYP (3-21G)] using Gaussian 09W. The output summary can be seen to the right of the page aswell as the full output file being linked here (BH3_OPTIMIZATION_JA2209.LOG)
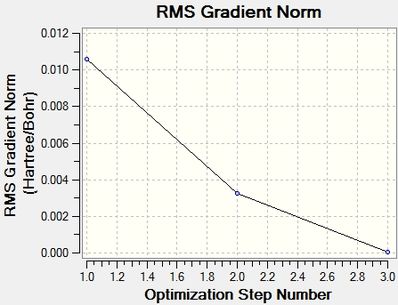
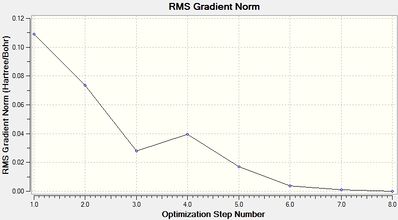
The optimization process can be summarized by the following animation or its individual frames where at first the bonds are not "bonded" as the position of the hydrogen atoms are moved accordingly until the energy is at a minimal. A discussion of "What is a Bond?" can be seen later in the investigation. The following graphs can summarize to optimzation process with each iteration lowering the energy and loweing the RMS Gradient with the lowest being the most negative energy and RMS gradient closest to zero. This information will be provided for each optimization. Optimization follows a number of iterations with lowering energy until the change in energy between iterations (i.e the gradient of the potential energy surface) should be zero shown by the RMS gradient becoming zero.
Filename = H:/COMPLABS/Module 2/BH3/BH3OPTIMIZATION.LOG BH3 Optimization. Ja2209. File Name = BH3OPTIMIZATION File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 3-21G Charge = 0 Spin = Singlet E(RB3LYP) = -26.46226433 a.u. RMS Gradient Norm = 0.00004507 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 10.0 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
|
 |
 |
From the optimization the point group can be confirmed as D3h with a Dipole Moment of 0.00 Debeye. Also all B-H bond lengths are equal to 1.19Å with the boron central atom having a bond angle of 120° (which corresponds to the literature[1] vales). The optimization is show to have 4 iterations to reach its minima in energy of -26.46 a.u. with a gradient of 0.00005 a.u. with a CPU time of just 10.0 seconds.
Vibrational Analysis
Frequency analysis was carried out on the optimized structure using the same method and basis set [DFT: B3LYP (3-21G)] with the vibrations tabulated below with the .LOG file provided here (BH3_FREQ_JA2209.LOG)
| Tabulated Data with Links to Animations | Vibrational Spectrum | |||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
From the .LOG file and the data above it can be seen that no large negative frequencies (usually only seen in transition states) therefore the frequency analysis was a success. 6 Modes were calculated all matching literature data very well. From the comparison to literature it can be seen that the calculated results are very similar to that of the ones published. Therefore there is enough proof to say that the very basic basis sets used in these calculations still give accurate results for simple compounds.
Molecular Orbital Analysis
The Molecular Orbitals were calculated with the basis set [DFT: B3LYP (3-21G)] with the additional keywords [pop=full] and NBO set to full. BH3_MO_JA2209.LOG This input file (.gjf) was set to the high performance computer (HPC) server with the D-space repository link in the table of data. The first 8 MO's were visualized (linked) with their energies tabulated below.
| Alpha MO | Energy (kcalmol-1) | Symmetry |
|---|---|---|
| 1 | -6.73023 | 1a1' |
| 2 | -0.51778 | 2a1' |
| 3 | -0.35689 | 1e' |
| 4 | -0.35689 | 1e' |
| 5 | -0.07455 | 1a2 |
| 6 | 0.18879 | 2e' |
| 7 | 0.18879 | 2e' |
| 8 | 0.19236 | 3a1' |
| DOI:10042/to-11875 |
From these calculated MO's a LCAO MO diagram was drawn, seen below (full resolution here) with the calculated MO's next to each LCAO MO for comparison.
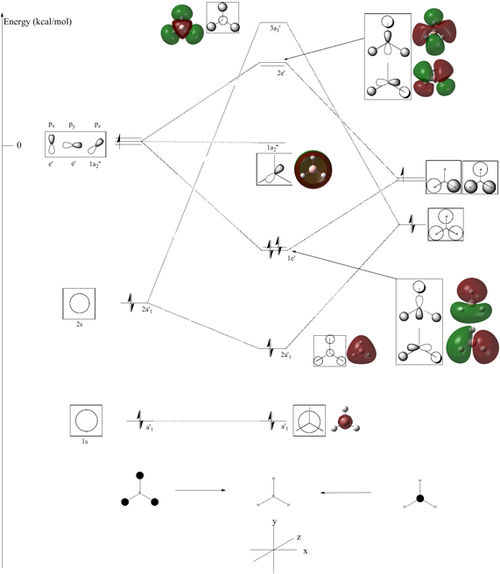
From the diagram it can be seen that the shapes of the calculated orbitals are very similar to that of the LCAO. The ordering of MO's 6,7,8 can be debated in LCAO and this corresponds to this with orbitals 6,7 and 8 having very similar energies (difference of 0.00357a.u.) These similarities in shape and order with LCAO/Gaussian shows that there is a certain accuracy to this relatively basic approach to computational analysis.
This shows qualitative MO theory is very useful and relatively accurate.
NBO Analysis
NBO Analysis allows the charge distribution/density of a compound to be visualized. This information allows prediction of reactivity and solvent interactions from the data seen in the table below shows that the boron holds a relativity large positive charge which would be expected due to it can act as a Lewis Acid therefore can accept a lone pair of electrons into its non-bonding vacant pz orbital. With smaller negative charges lying on each of the hydrogen placed symmetrically around the boron meaning there is no-overall dipole moment as shown in the Optimization step before.
 |
 |
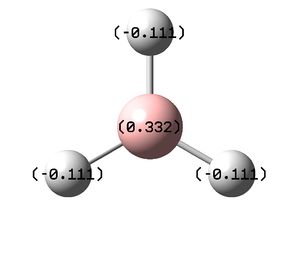Charge Populations Analysis is shown below, its summarizes the location of electrons on each atom in the compound and can be seen as a text version of the images above showing the charge of each atom and the number of electrons localized to that atom.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33161 1.99903 2.66936 0.00000 4.66839
H 2 -0.11054 0.00000 1.11021 0.00032 1.11054
H 3 -0.11054 0.00000 1.11021 0.00032 1.11054
H 4 -0.11054 0.00000 1.11021 0.00032 1.11054
=======================================================================
* Total * 0.00000 1.99903 6.00000 0.00097 8.00000
Bond Orbital Coefficients/Hybrids are also important the first 6 NBO's data is show below the key points to take from this analysis is the bonding orbitals between boron and all the hydrogens have 33.33% s-character and 66.67% p-character which is equivalent to a sp2 hybridized orbital explaining the 120° bond angle which 44.49% is contributed by boron and 55.52% by hydrogen. And secondly orbital 5 which is the empty non-bonding orbital which allows borane to be a Lewis Acid has 100% s-character. This should not be the case as stated before the accepting orbital is the pz orbital on borane. I am not sure of the source of this discrepancy but it is most likely due to the relatively basic basis set used in these calculations.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99853) BD ( 1) B 1 - H 2
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99853) BD ( 1) B 1 - H 3
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99853) BD ( 1) B 1 - H 4
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99903) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
As thought the Second Order Perturbation Theory Analysis shows nothing of real interest due to there is no orbital mixing in BH3
Computational Analysis of TlBr3
Aims and Objectives
To apply some of the techniques in the structural analysis of BH3 to a molecule containing heavier atoms and therefore requiring pseudo-potentials. Thallium is highly toxic and therefore using this approach we can estimate certain properties of the compound without the danger of exposure. Due to its high molecular weight and therefore number of electrons (Bromine- 35, Thallium-81) these calculations will be effected by relativistic effects. To compensate for the Schrodinger equation not being able to account for these pseudo-potentials are used. This special function freezes the core electrons to the nucleus of there respective atom and then only take into account for the valence electrons, this greatly decreases CPU time but is generally less accurate when not used in conjunction with a full electron basis set.
Optimization
TlBr3 was drawn in Gaussian 5.0. The symmetry group was restricted to D3h with a very tight tolerance of 0.0001, this was then optimized using [DFT: B3LYP (LanL2DZ)].
The optimization process summary can be seen below:
TlBr3_optimzation File Name = tlbr3_op_ja2209 File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RHF) = -89.04301362 a.u. RMS Gradient Norm = 0.00002629 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 9.0 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000053 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.000447 0.001800 YES
RMS Displacement 0.000293 0.001200 YES
Predicted change in Energy=-3.746478D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.5668 -DE/DX = 0.0001 !
! R2 R(1,3) 2.5668 -DE/DX = 0.0001 !
! R3 R(1,4) 2.5668 -DE/DX = 0.0001 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
|
 |
 |
From the summary it can been seen the optimized Tl-Br bond distance is 2.78Å with a bond angle of 120° which are relatively close to the literature[2](2.51Å, 120°). This optimization was then sent for frequency analysis to cofirm it is a minima. If a optimization is not a minima it will most likely have large negative vibrational frequencies.
Other points of interest from the optimization are, Final energy = -89.04301362 a.u., Final Gradient=0.00002629 a.u., Number of iterations:3 and Dipole Moment=0.00 Debeye
Vibrational Analysis
Frequency analysis was carried out using the same method (B3LYP) and basis set (LANL2DZ) as optimization due to the fact if different ones were used there could be no comparison between the two due to all calculated values would change. The input file (.gjf) was sent to the HPC server and the results published to D-space (DOI:10042/to-11884 ) and the .LOG files provided here (TlBR3_freq_ja2209.out). The data was tabulated below:
| Tabulated Data with Links to Animations | Vibrational Spectrum | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
From the .LOG file there is no relative low frequencies confirming this structure is a minima in energy. The low frequencies (see below) show the first "real" mode is at 40.53cm-1 which is an order of magnitude larger than the lowest frequencies confirming that this calculations have a relatively high accuracy level.
Low frequencies --- -0.9217 -0.0053 -0.0014 0.0145 4.2026 4.2026 Low frequencies --- 40.5306 40.5311 43.3433
The literature[2] value for the IR is not tabulated but fits relatively to the shape in the full report. Overall it can be seen that with the use of pseudo-potentials a relatively accurate idea of structure and properties of a molecule can be calculated again using MO theory.
What is a Bond?
A covalent bond in the simplest form which is what is used to visualize a bond is a physical link between two atoms. Obviously this can be used to summarize what a bond is however a bond is a sharing of electron density of valence electrons. This for the atoms found in organic molecules is usually a pre-set distance that can be summarized by a visual connection which can be affected by electron sinks/sources around the bond however this distance is not pre-set for heavier atoms or less commonly used atoms therefore gaussian calulated were the best distance is for overlap to occur and places the atom there without showing this physical connection. When you look at the MO's the connection is there because a bond is a sharing of electron density, thereofre in gaussian and the jmol provided if there is a visual bond doesnt mean there isnt one. With quantum mechanics if there is overlap there is a interaction and if that interaction is stong enough it is deem a "bond".
Isomers of Mo(CO)4L2
Aims and Objectives
To investigate multiple optimizations using increasing more detailed basis sets to further optimize the compound further each time and to use this optimized data to compare the relative energies of each isomer to determine which may rationalize which each isomer may be seen experimentally and how to distinguish each isomer spectroscopically.
Optimization of the two Isomers
Initial Optimization Using LANL2MB
The first optimization used was Method: B3LYP and Basis Set: LANL2MB which is a low level basis set and pseudo-poteintal to get the rough geometry right. This first optimization also had the additional word "opt=loose" this sets the convergence criteria to a less accurate number.
All optimization data is below the key points are the following:
- Final Energy: cis= -617.11 a.u. / trans= -617.14 a.u.
- With these rough optimizations it appears that the cis and trans isomers are very close in energy however further optimization may change this.
- Point Group: cis= C1 / trans= C1
- C1 symmetry for both compound are not expected, this is probably due to slight distortions in the symmertry caused by the optimization making an asymmetric nature, the cis-Isomer should be C2v and the trans-Isomer should be D4h. (when the Cl's are eclipsed)
- Dipole Moment: cis= 2.73 Debye / trans= 0.00 Debye
- This shows that having the asymmetric ligands cause a dipole moment in the compound which is to be expected, however the trans each charge associated with a ligand is canceled by the same ligand on the other side of the octahedral complex.
- CPU Time:cis= 0:11:35 / trans= 0:7:49
| Summary | Convergence |
Cis-Optimization-One File Name = cis_op_ja2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.10979392 a.u. RMS Gradient Norm = 0.11007691 a.u. Imaginary Freq = Dipole Moment = 2.7305 Debye Point Group = C1 Job cpu time: 0 days 0 hours 11 minutes 35.1 seconds. Optimized LANL2MB Structure |
Item Value Threshold Converged?
Maximum Force 0.000219 0.002500 YES
RMS Force 0.000070 0.001667 YES
Maximum Displacement 0.008487 0.010000 YES
RMS Displacement 0.003037 0.006667 YES
Predicted change in Energy=-1.642817D-06
Optimization completed.
-- Stationary point found.
|
 |
 |
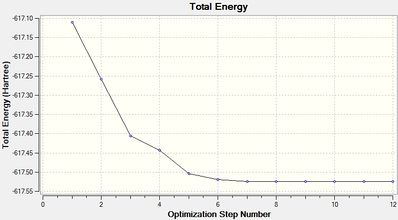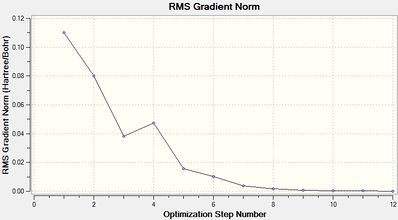| Summary | Convergence |
Trans-Isomer Op1 File Name = trans_op_ja2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.14019676 a.u. RMS Gradient Norm = 0.10924975 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C1 Job cpu time: 0 days 0 hours 7 minutes 48.7 seconds. Optimized LANL2MB Structure |
Item Value Threshold Converged?
Maximum Force 0.000187 0.002500 YES
RMS Force 0.000056 0.001667 YES
Maximum Displacement 0.003592 0.010000 YES
RMS Displacement 0.001020 0.006667 YES
Predicted change in Energy=-6.646453D-07
Optimization completed.
-- Stationary point found.
|
 |
 |
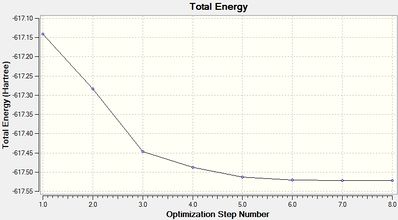Secondary Optimization Using LANL2-DZ
The second optimization uses the same method (B3LYP) and a slightly larger basis set (LANL2DZ) with normal optimisation criteria (i.e. no "opt=loose") but with an increased electronic convergence with the addtional keywords "int=ultrafine scf=conver=9". Before this optimization was calculated the dihderal angles were set to a certain geometry. This geometry was found to be a minima by Dr.Hunt mentioned on inorganic lab wiki. The cis-Isomer was set to have the Cl staggered to each other and in the trans-Isomer they were eclipsed. They were then sent off for optimization with all data listed below but with the key points of interest noted here:
- Final Energy: cis= -623.54 a.u. / trans= -623.54 a.u.
- Two points to make from these new energies, the first being the energy has decresed for both compound with this new optimization as expected (both ~6a.u.). Secondly the energies for both complexes are still the same.
- Point Group: cis= C1 / trans= C1
- Dipole Moment: cis= 3.10 Debye / trans= 0.01 Debye
- With this new optimization the dipole moment for cis has increased and the trans now has a very low dipole moment, however this is most likely either an error or due to a small amount of asymmetric distortion on the structure during the optimization.
- CPU Time:cis= 1:08:26 / trans= 0:48:06
- The main point from the CPU time is it has greatly increased for both isomers, expected for this more complex larger basis set.
| Summary | Convergence |
cis180_op_ja2209 File Name = cis180_scan_op_ja2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.54012496 a.u. RMS Gradient Norm = 0.01820011 a.u. Imaginary Freq = Dipole Moment = 3.0919 Debye Point Group = C1 Job cpu time: 0 days 1 hours 8 minutes 26.0 seconds. Optimized LANL2DZ Structure |
Item Value Threshold Converged?
Maximum Force 0.000032 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.001430 0.001800 YES
RMS Displacement 0.000437 0.001200 YES
Predicted change in Energy=-1.755166D-08
Optimization completed.
-- Stationary point found.
|
 |
 |
| Summary | Convergence |
transo_op_ja2209 File Name = trans0_scan_ja2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.54165081 a.u. RMS Gradient Norm = 0.01779635 a.u. Imaginary Freq = Dipole Moment = 0.0492 Debye Point Group = C1 Job cpu time: 0 days 0 hours 47 minutes 6.2 seconds. Optimized LANL2DZ Structure |
Item Value Threshold Converged?
Maximum Force 0.000068 0.000450 YES
RMS Force 0.000022 0.000300 YES
Maximum Displacement 0.001218 0.001800 YES
RMS Displacement 0.000239 0.001200 YES
Predicted change in Energy=-9.552148D-08
Optimization completed.
-- Stationary point found.
|
 |
 |
Advanced Optimization Using dAO
The third, final and optional optimization used a method of B3LYP and a basis set based around LANL2DZ again however due to Phosphorous' low lying d-orbitals it is happy to become hypervalent therefore the manual addition of an extra basis set was used. Using the keyword "extrabasis" in additional keywords the .gjf was opened as a text file and the following basis set was added to the end of the document:
(blank line) P 0 D 1 1.0 0.55 0.100D+01 **** (blank line)
This was then sent off to be optimized with all the data tabulated below with again the key points of interest here:
- Final Energy: cis= -623.60 a.u. / trans= -623.70 a.u.
- The decrease in energy between the second and third basis set is very small showing that Phosphorous' low lying d-orbitals were not having a large effect the overall energy of the complexes. And still the energies are very similar in terms of atomic units. A more in depth discussion on energies will be seen later in the report.
- Point Group: cis= C1 / trans= C1
- Dipole Moment: cis= 3.12 Debye / trans= 0.00 Debye
- CPU Time:cis= 1:24:29 / trans= 0:53:54
- Again it can be seen that the more advanced basis set (only one extrabasis) has increased CPU time again.
| Summary | Convergence |
cis180_op_ja2209 File Name = cis_scan_advop_ja2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -623.59959896 a.u. RMS Gradient Norm = 0.02255102 a.u. Imaginary Freq = Dipole Moment = 3.3149 Debye Point Group = C1 Job cpu time: 0 days 1 hours 24 minutes 28.6 seconds.. Optimized dAO Structure |
Item Value Threshold Converged?
Maximum Force 0.000021 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.001024 0.001800 YES
RMS Displacement 0.000294 0.001200 YES
Predicted change in Energy=-9.683940D-09
Optimization completed.
-- Stationary point found.
|
 |
 |
| Summary | Convergence |
transo_op_ja2209 File Name = trans_scan_adv_op_ja2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = Gen Charge = 0 Spin = Singlet E(RB3LYP) = -623.69415458 a.u. RMS Gradient Norm = 0.00012746 a.u. Imaginary Freq = Dipole Moment = Debye Point Group = C1 Job cpu time: 0 days 0 hours 53 minutes 53.8 seconds. Optimized dAO Structure |
Item Value Threshold Converged?
Maximum Force 0.000094 0.000450 YES
RMS Force 0.000017 0.000300 YES
Maximum Displacement 0.001744 0.001800 YES
RMS Displacement 0.000353 0.001200 YES
Predicted change in Energy=-1.659152D-07
Optimization completed.
-- Stationary point found.
|
 |
 |
Discussion
Difference in Energies
With a final difference in energy of 0.1a.u. (62.7 kcalmol-1) this shows that the energy to make isomerisation occur is quite high which fits with the experimental method in the second year lab experiment. However this is a lot higher than expected it may be in this case the advanced dAO method has failed in some aspect due to the difference in energy for the second basis set used LANL2DZ has an energy difference of 0.001 a.u. (6.27 kcalmol-1) which is what the expected magnitude of the value should be.
Effects of Altering Ligands
To stabilize on the the trans or cis ligands over the other would probably be a issue of sterics over electronics, for example if the PCl3 ligand was substituted for a larger P(Mes)3 this would force linearity of the P-M-P bond due to larger steric clashing if it were in the cis position. However this is an extreme, substituting it for a PMe3 or PBr3 I believe would favor the trans over the cis. Using this idea it could it be said that this effect would occur the other way with smaller ligands? I dont believe so the smaller the ligand the less the trans is favored but the cis becomes no less favored. This is were it becomes a electronic matter which would require additional calculations and most probably MO analysis to resolve.
Vibrational Frequency Analysis
The vibrational analysis was calculated via the HPC sever using the same method and basis set as the final optimization including the dAO basis set.
Here are the DOI links to each of the HPC submitted calculations: cis:DOI:10042/to-11916 trans:DOI:10042/to-11917
Here are links to each of the .LOG files from each of the calculations: cis:Cis_scan_freq_ja2209.out trans: Trans_scan_freq_ja2209.out
All the vibrational modes of importance are tabulated below (please note there are many more modes I have selected ones of interest) but the main points are listed below:
- C=O stretches
- The isomers have 4 vibrational modes present, however the difference with the two isomers is that the symmetric stretch of the cis-Isomer is IR active due to the asymmetric nature of the whole complex where in the trans-Isomer the symmetric stretch is not IR active and does not show up on the IR spectrum. This can be seen the the zoomed in spectrum where there is an additional peak around 2000cm-1 this is how to differentiate between the two isomers spectroscopically.
- Comparison to literature
From both tables it can be seen that each spectra matches the experimental/literature shapes of IR with one being one peak and the other being two. However the difference in terms of wavenumbers there is a relative accuracy with no large differences. This shows even with still a relatively small basis set you can gain accurate results.
cis-Isomer
| Tabulated Data with Links to Animations | Vibrational Spectrum | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
 |
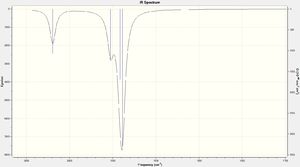(N.B.-The literature only has two peaks present in its data due to the overlap of the 3 asymmetric stretches showing up as one larger peak.)
trans-Isomer
| Tabulated Data with Links to Animations | Vibrational Spectrum | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
 |
 |
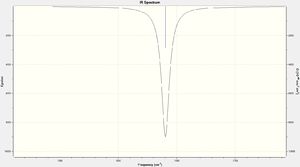(N.B. The literature comparison in this table is taken from the experimental data I obtained during the spring term of 2nd years synthesis term experiment with the full report explaining the source of the difference in IR in more detail linked here: Full Report)
Low and Negative Frequencies
cis-Isomer:
Low frequencies --- -1.7543 -0.9384 -0.0006 -0.0006 -0.0006 1.4180 Low frequencies --- 11.5742 20.1282 45.8164
trans-Isomer:
Low frequencies --- -0.0004 0.0003 0.0003 38.1416 38.4093 63.0770 Low frequencies --- 67.8857 68.2114 81.8352
All of these movements are wags of all the ligands around the metal center all with relativity small motion, these will readily happen at RTP and at probably the cause of the loss in symmetry of octahedral complexes allowing charge transfers and electron excitements to occur without being symmetrically forbidden. They also seem to concentrate on the PCl3 groups explaining the motion in these absorptions are why isomerism can occur at such low temperatures . Another point to make is that none of them are largely negative showing that both of these isomers are minimas in energy for the complex can not transition states which show negative frequencies.
Mini Project
Aims and Objectives
The aim of this project is to use the techniques used in the previous investigations and to apply them to an interesting problem in Inorganic chemistry. With this problem I will run calculations including optimization, vibrational analysis and molecular orbital visualization to highlight the cause of a particular trend or non-trend within a small group of molecules. Analyzing my results I will be able to form a justifiable argument to why or why not a particular effect is occurring.
Introduction
Halogen Azides are important in inorganic synthesis[4] allowing the addition of the azide (N3) ligand to be added to a particular complex, this the azide structure it can form single or multiple bonds to the metal center in difference cases allowing a catalytic pathway to be opened up or adjust the reactivity or stereoselectivity of a complex interacting with a substrate. In this particular investigation I will be looking at the stability/non-stability of 3 different azide complexes; Hydrogen azide (Hydrazoic Acid), Fluorine azide and Chlorine azide and look at the stability of each of the compounds and the reason for each of their relative energies and whether they are electronic properties or other properties.
Choosing Basis Set
Three Basis set's were used on all the compounds shown above, to see how affective they were and which one was most appropriate for this Mini Project, all the compounds were drawn in Gaussview 5.0 and were optimized using 3 different basis sets all using the same method.
The three basis sets under examination are:
[DFT: B3LYP (LAN2DZ)]
[DFT: B3LYP (6-31+G(d))]
[DFT: B3LYP (6-211+G(d))]
The compounds were run with all basis sets however to keep the report from being overally long only two will be mentioned on the wiki site. The LAN2DZ is a pseudo-potential like double zeta basis set which fixes the core electrons in place although taking them into account focus's mostly on the valence electrons witch relative accuracy with heavier atoms. The second basis set used was 6-31+G(d) is a full electron double zeta basis set that is the most commonly used throughout computational chemistry for its quick CPU time and relatively accurate results. The third a is more accurate full electron triple basis set that is a lot more accurate but a lot more costly in terms of calculation time, however using small molecules in this investigation may be applicable to use.
The following summarys for the optimization for HN3 are below between 6-31+G(d) and 6-311+G(d) to find whether it is worth the extra computational time to use this more advanced basis set
| LAN2DZ | 6-31+G(d) | 6-311+G(d) |
|---|---|---|
File Name = LAN_OP_H_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -164.73457647 a.u. RMS Gradient Norm = 0.00005726 a.u. Imaginary Freq = Dipole Moment = 2.2694 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 28.0 seconds. |
File Name = 631_OP_H_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31+G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -164.79008716 a.u. RMS Gradient Norm = 0.00007544 a.u. Imaginary Freq = Dipole Moment = 2.0193 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 46.0 seconds. |
File Name = 6311_OP_H_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-311+G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -164.83175748 a.u. RMS Gradient Norm = 0.00018353 a.u. Imaginary Freq = Dipole Moment = 2.0345 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 50.0 seconds. |
From the three summaries it can be sen for HN3 all basis sets have come to the relatively same results with a difference in energy between the three around 0.1 a.u. This means for H the basis sets are suitable, the problem will be when core electrons are introduced for the other compounds, the real comparison is between 6-31+G(d), 6-311+G(d) where there is a 0.04 a.u. energy difference and a increase of 10% CPU time increase. This this is mine for the heavier atoms where CPU time may be significantly larger for this project I will use 6-31+G(d).
Optimization
The three molecules were optimized using the two selected basis sets, all the summaries, proof of convergence, jmol's are provided below. The main points of interest is that the stabilization energy of the addition of the fluorine is nearly 100 a.u. comparatively to the hydrogen compound. This shows there is a signicant stablisiation with the flurine which is more so than in the chlorinated compound (stabilization energy ~15 a.u.) meaning it is a cause most likely of an electronic interaction.
HN3
| LAN2DZ | 6-31+G(d) |
|---|---|
File Name = LAN_OP_H_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -164.73457647 a.u. RMS Gradient Norm = 0.00005726 a.u. Imaginary Freq = Dipole Moment = 2.2694 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 28.0 seconds. |
File Name = 631_OP_H_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31+G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -164.79008716 a.u. RMS Gradient Norm = 0.00007544 a.u. Imaginary Freq = Dipole Moment = 2.0193 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 46.0 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000144 0.000450 YES
RMS Force 0.000074 0.000300 YES
Maximum Displacement 0.000305 0.001800 YES
RMS Displacement 0.000177 0.001200 YES
Predicted change in Energy=-3.269192D-08
Optimization completed.
-- Stationary point found.
|
Item Value Threshold Converged?
Maximum Force 0.000205 0.000450 YES
RMS Force 0.000105 0.000300 YES
Maximum Displacement 0.000237 0.001800 YES
RMS Displacement 0.000164 0.001200 YES
Predicted change in Energy=-3.639107D-08
Optimization completed.
-- Stationary point found.
|
FN3
| LAN2DZ | 6-31+G(d) |
|---|---|
File Name = LAN_OP_F_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -263.90563219 a.u. RMS Gradient Norm = 0.00023182 a.u. Imaginary Freq = Dipole Moment = 1.4515 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 33.0 seconds. |
File Name = 631_OP_F_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31+G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -263.95053343 a.u. RMS Gradient Norm = 0.00001738 a.u. Imaginary Freq = Dipole Moment = 1.1207 Debye Point Group = CS Job cpu time: 0 days 0 hours 1 minutes 18.0 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000363 0.000450 YES
RMS Force 0.000195 0.000300 YES
Maximum Displacement 0.000502 0.001800 YES
RMS Displacement 0.000336 0.001200 YES
Predicted change in Energy=-1.913123D-07
Optimization completed.
-- Stationary point found.
|
Item Value Threshold Converged?
Maximum Force 0.000027 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.000176 0.001800 YES
RMS Displacement 0.000115 0.001200 YES
Predicted change in Energy=-3.042649D-09
Optimization completed.
-- Stationary point found.
|
ClN3
| LAN2DZ | 6-31+G(d) |
|---|---|
File Name = LAN_OP_CL_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -179.03003498 a.u. RMS Gradient Norm = 0.00009052 a.u. Imaginary Freq = Dipole Moment = 0.7968 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 33.0 seconds. |
File Name = 631_OP_CL_JA2209 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31+G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -624.34031078 a.u. RMS Gradient Norm = 0.00011356 a.u. Imaginary Freq = Dipole Moment = 0.5054 Debye Point Group = CS Job cpu time: 0 days 0 hours 1 minutes 29.0 seconds. |
Item Value Threshold Converged?
Maximum Force 0.000243 0.000450 YES
RMS Force 0.000122 0.000300 YES
Maximum Displacement 0.000350 0.001800 YES
RMS Displacement 0.000235 0.001200 YES
Predicted change in Energy=-5.202096D-08
Optimization completed.
-- Stationary point found.
|
Item Value Threshold Converged?
Maximum Force 0.000316 0.000450 YES
RMS Force 0.000137 0.000300 YES
Maximum Displacement 0.000313 0.001800 YES
RMS Displacement 0.000275 0.001200 YES
Predicted change in Energy=-8.681700D-08
Optimization completed.
-- Stationary point found.
|
Structural Analysis
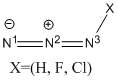
| HN3 | FN3 | ClN3 | |||||||||
| LAN2DZ | 6-31+G(D) | LAN2DZ | 6-31+G(D) | LAN2DZ | 6-31+G(D) | ||||||
| Bond | Length (Å) | Bond | Length (Å) | Bond | Length (Å) | Bond | Length (Å) | Bond | Length (Å) | Bond | Length (Å) |
| N1-N2 | 1.17 | N1-N2 | 1.14 | N1-N2 | 1.17 | N1-N2 | 1.14 | N1-N2 | 1.17 | N1-N2 | 1.14 |
| N2-N3 | 1.27 | N2-N3 | 1.24 | N2-N3 | 1.30 | N2-N3 | 1.26 | N2-N3 | 1.29 | N2-N3 | 1.25 |
| N3-H | 1.03 | N3-H | 1.02 | N3-F | 1.50 | N3-F | 1.44 | N3-Cl | 1.92 | N3-Cl | 1.78 |
| Bond | Angle | Bond | Angle | Bond | Angle | Bond | Angle | Bond | Angle | Bond | Angle |
| N1-N2-N3 | 170° | N1-N2-N3 | 171° | N1-N2-N3 | 172° | N1-N2-N3 | 171° | N1-N2-N3 | 172° | N1-N2-N3 | 171° |
| N2-N3-H | 113° | N2-N3-H | 110° | N2-N3-F | 104° | N2-N3-F | 105° | N2-N3-Cl | 109° | N2-N3-Cl | 110° |
| 631_OP_H_JA2209.LOG | 631_OP_F_JA2209.LOG | 631_OP_Cl_JA2209.LOG | |||||||||
All the strucutal data fit relativlty well with the literature[5]. Comparing the structural data of the three compounds it can be seen that both basis sets. All three compounds have very similar bond lengths and angles, the only trend of interest may be the lengthening of the N2-N3 bond with the addition of fluorine and a small lengthening with the addition of Cl, this may be due to a electronic orbital interaction being less effective with Cl due to its larger orbitals having less effective overlap with Nitrogen. However this will be discussed in the MO section of this project.
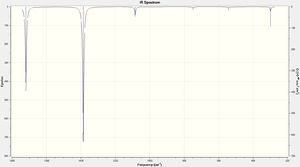
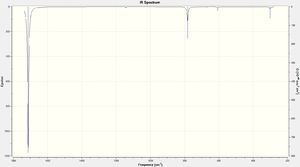
Vibrational Analysis
Using the full electron basis set the following vibrational spectra were calculated:
 |
 |
 | ||||||
| Mode | Frequency | Intensity | Mode | Frequency | Intensity | Mode | Frequency | Intensity |
| 1 | 558.42 | 42.05 | 1 | 298.92 | 6.90 | 1 | 302.05 | 4.68 |
| 2 | 652.07 | 5.74 | 2 | 544.04 | 2.33 | 2 | 607.39 | 3.39 |
| 3 | 1073.96 | 195.51 | 3 | 748.29 | 2.36 | 3 | 669.92 | 0.45 |
| 4 | 1131.45 | 20.77 | 4 | 1084.54 | 12.50 | 4 | 782.63 | 33.41 |
| 5 | 1814.91 | 373.10 | 5 | 1385.85 | 212.43 | 5 | 1142.65 | 1.68 |
| 6 | 3738.41 | 57.69 | 6 | 1718.81 | 131.58 | 6 | 1712.73 | 335.52 |
| 631_FR_H_JA2209.LOG | 631_FR_F_JA2209.LOG | 631_FR_CL_JA2209.LOG | ||||||
| DOI:10042/to-11999 | DOI:10042/to-11998 | DOI:10042/to-11997 | ||||||
From these spectra and vibrational modes the following points are interest are:
- A free N-F bond as the frequency of 992.26cm-1 (calculated from gaussian using same method and basis set) however in FN3 it is at 1814.91cm-1 showing it as significantly stronger implying some form of resonance with the nitrogen charge system.
- The same effect can be seen with N-Cl stretch but to a lesser extent implying the same effect is occurring but to a lesser extent meaning Cl is less effective at stabilizing the azide probably due to a less effective orbital overlap due to size difference however this will be discussed in the MO section of the report. (compound N-Cl stretch 782.63cm-1 free calculated N-Cl stretch 715.02cm-1.
- With the N-H stretch is is slightly weaker than it should be (compound N-H stretch 3738cm-1 and free N-H stretch calculated at 3842.44cm-1) meaning this effect is not seen with hydrogen but rather the oppisite making me believe it is due to the electron denssity/ electronegativity of the substituent effecting its magnitude as well as the substituent size.
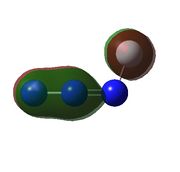
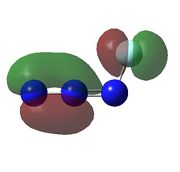
MO Analysis
| Calculated Molecular Orbitals For FN3 | ||||||
 |
 |
 |
 |
 |
 |
 |
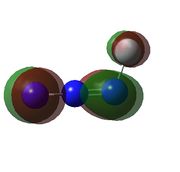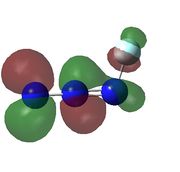| Energy= -0.47830 | Energy= -0.45824 | Energy= -0.36955 | Energy= -0.29074 | Energy= -0.13016 | Energy= -0.04830 | Energy= 0.01666 |
| HOMO-3 is bonding orbital in the azide chain and a lone pair on the fluorine, there would be very weak antibonding interaction between the two orbitals | HOMO -2 the same as HOMO-3 but due to lone pair on fluorine is closer to bonding orbital on azide chain, this orbital is higher in energy. | HOMO -1 is the real orbital of interest
and is in a more in depth comparison below. |
HOMO: antibonding orbital between N1, N3 and F. | LUMO: antibonding orbital between N1, N2 and F with slight bonding interaction between N2 and N3 | LUMO+1: antibonding orbital between all atoms. | LUMO+2: extreme antibonding orbital in the azide chain. |
| Calculated HOMO-1 For HN3, FN3 and ClN3 | ||
 |
|
 |
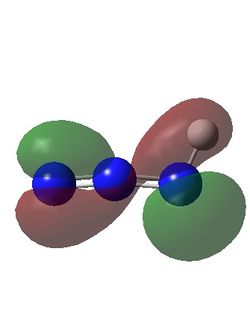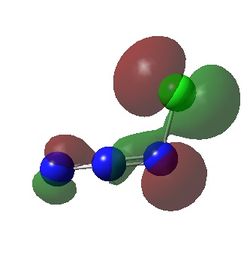| DOI:10042/to-12001 | DOI:10042/to-12000 | Unable to upload to D-space Job ID: 54458 |
| 631_MO_H_JA2209.LOG | 631_MO_F_JA2209.LOG | 631_MO_CL_JA2209.LOG |
The HOMO-1 for all three compounds show the source of the stablity of the structure with there corresponding substituents. In the case of Fluorine a good overlap of a lone pair orbital and the azide resonance orbital (i.e partially antibonding N2-N3 bond and bonding N1-N2 bond) is seen with full incorporation of its orbital with the azide system. This is expected due to fluorine and nitrogen being similar in size. A simlar effect can be seen with chlorine however due to less effective overlap with the bonding orbitals due to the difference in size of nitrogen and chlorine the orbital is smaller and less consistent along the azide group therefore the acceptor orbital is the lone pair on N2 explaining why the stabilization in Cl substituted azide is less. This also explains the higher frequency in the vibrational spectra with a higher bond order between the N-F/N-Cl with N-F>N-Cl.
Looking at the HN3 a similar effect is seen to stabilize the azide chain however the donor orbital is actually the azide group and the acceptor orbital is the σ*N-H orbital corresponding the the weaker frequency seen in the vibrational spectrum.
Hopefully all these interactions and orbial contributions will be seen in the NBO analysis.
NBO Analysis
Charge Distribution
| Representation | HN3 | FN3 | ClN3 |
|---|---|---|---|
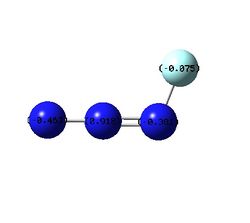
| Charge Distribution Summarized By Color |  |
 |
 |
| Charge Distribution Summarized By Number |  |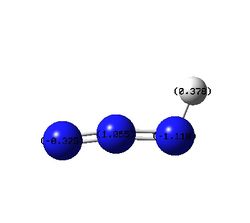
 |
 |
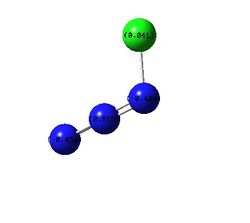The only points of interest in the charge distrubution is that without a halide N3 is a lot more positive than with a halide. And that overall the Fluorine is slightly negative implying electron withdrawing nature and chlorine is slightly positive implying electron donating behavior to gain insight into this the orbital coefficients must be looked at.
Second Order Perturbation Theory
This application of second order peturbation theory gave large amount of splitting interations with the most being caused by the moving of charge around the azide group however it terms of comparing between the compounds the splitting of interest for FN3 and ClN3 is copied straight from the .log file and provided below:
FN3
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
12. LP ( 2) N 3 / 73. BD*( 2) N 1 - N 2 208.21 0.13 0.147
15. LP ( 3) F 4 / 33. RY*( 4) N 2 2.31 2.41 0.067
15. LP ( 3) F 4 / 73. BD*( 2) N 1 - N 2 17.68 0.35 0.084
ClN3
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
15. LP ( 2) N 3 / 78. BD*( 2) N 1 - N 2 152.48 0.18 0.147
18. LP ( 2)Cl 4 / 76. BD*( 1) N 1 - N 2 4.18 0.92 0.055
19. LP ( 3)Cl 4 / 15. LP ( 2) N 2 27.15 0.08 0.075
The donation from the F into the B* N1-N2 is its predominate splitting, this has a lower energy stabilisation than that of Cl's donation to the N2 LP however, fluorine's interaction increases the stability of the azide resonance with a massive stabilization of charge moving around the azide chain whereas the Cl effect is larger but reduces the more important azide charge transfer stabilization meaning overall it is less effective at stabilizing the molecule. HN3
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
4. BD ( 3) N 1 - N 2 / 59. BD*( 1) N 3 - H 4 4.43 0.95 0.058
10. LP ( 2) N 2 / 57. BD*( 2) N 1 - N 2 122.94 0.21 0.143
The effect is seen where it is the the other way round in the HN3 compound where the azide interacts with the N-H bond stabilizing the system overall but weakening the N-H bond and lowering the stability caused by the cahrge transfer around the azide even more.
Orbital Coefficients
The orbitals under investigation where taken straight from the .log file
HN3
5. (1.92137) BD ( 1) N 2 - H 3
( 69.53%) 0.8338* N 2 s( 20.02%)p 3.99( 79.84%)d 0.01( 0.14%)
-0.0010 0.4467 -0.0158 -0.0205 0.0003
0.8739 -0.0128 -0.0133 -0.1808 0.0401
-0.0020 0.0000 0.0000 0.0000 0.0155
0.0000 0.0000 0.0274 -0.0209
( 30.47%) 0.5520* H 3 s(100.00%)
FN3
5. (1.97436) BD ( 1) N 3 - F 4
( 35.70%) 0.5975* N 2 s( 17.40%)p 4.72( 82.19%)d 0.02( 0.41%)
-0.0005 0.4108 -0.0719 -0.0072 0.0043
0.8535 0.0604 -0.0046 -0.2928 -0.0633
-0.0042 0.0000 0.0000 0.0000 -0.0114
0.0000 0.0000 0.0522 -0.0351
( 64.30%) 0.8019* F 4 s( 20.23%)p 3.94( 79.64%)d 0.01( 0.13%)
0.0001 0.4462 -0.0567 -0.0020 -0.0002
-0.8335 0.0299 0.0066 0.3173 -0.0110
-0.0065 0.0000 0.0000 0.0000 -0.0243
ClN3
5. (1.92201) BD ( 1) N 2 -Cl 4
( 55.07%) 0.7421* N 2 s( 13.87%)p 6.19( 85.84%)d 0.02( 0.29%)
-0.0009 0.3705 0.0172 -0.0337 0.0004
0.8875 0.0117 -0.0137 -0.2612 0.0473
0.0010 0.0000 0.0000 0.0000 0.0018
0.0000 0.0000 0.0400 -0.0359
( 44.93%) 0.6703*Cl 4 s( 10.14%)p 8.79( 89.12%)d 0.07( 0.75%)
0.0000 0.0006 0.3081 -0.0799 0.0049
0.0002 -0.0006 -0.8806 0.0848 0.0004
0.0003 0.3279 -0.0323 -0.0068 0.0000
0.0000 0.0000 0.0000 -0.0560 0.0000
0.0000 0.0484 -0.0446
These bonding orbitals between the azide nitrogen and the substituent it shows in hydrogen containing compound the bond lies more on the nitrogen as expected with hydrogens low electronegativity and the posistive charge lying on the azide chain, In the fluorine azide compound the bond lies slightly more on the fluorine which can be explained by fluorines high electronegativity and the fact the positive charge on the azide is being stabilized by resonance of its lone pair into the azide chain. With the chlorine the bond lies slightly more on the nitrogen explaining that the smaller electronegativity and the less effective pi resonance means that the nitrogen pulls its electron tighter than the chlorine can.
Conclusion
- Overall the fluorine donation of its lone pair is small but due to where its donation occurs allows an increased stability caused by charge transfer around the azide chain (also showing by the N-F bond is stronger than usual). With its large induction effect the fluorine overall is an electron withdrawing group. This is because of its lone pair donation the positive charge of the azide group is quenched and fluorine can pull the electrons from its bond with nitrogen closer to itself.
- With chlorine on the other hand a large stabilization caused by the donation which lowers the resonance stability of the N3 chain group overall have a less stabilizing effect on the compound. This can be seen with a slightly stronger N-Cl bond but overall less stable in terms of energy. This good overlap and less effective induction that fluorine means overall chlorine is electron donating.
- With hydrogen mainly used as a comparison in this investigation the same effect as flourines but with the azide acting as the donor orbital into the σ*N-H bond showing why the N-H bond is weaker than the free N-H bond. This effect is small and the inductive effect of the N-H bond means that the electron density lies closer to the azide meaning overall hydrogen is electron donating.
References
- ↑ 1.0 1.1 Schuurman, M. S., Allen, W. D. and Schaefer, H. F. (2005), The ab initio limit quartic force field of BH3. Journal of Computational Chemistry, 26: 1106–1112. doi: 10.1002/jcc.20238
- ↑ 2.0 2.1 Blixt, J. Glaser, J. Mink, J. Persson, I. Persson, P. Sandstroem, M. (1995) Structure of Thallium(III) Chloride, Bromide and Cyanide Complexes In Aqueous Solution Journal of American Chemical Society, 18 5089-5104
- ↑ Shakti, L. Steven, P. Nolan, C.D. Lopez, R. (1988) Heat of reaction of (norbornadiene)molybdenum tetracarbonyl with monodentate and bidentate ligands. Solution thermochemical study of ligand substitution in the complexes cis-L2Mo(CO)4 Inorganic Chemistry 27 81-85
- ↑ Dehnicke, K. (1967), Reactions of Halogen Azides. Angewandte Chemie International Edition in English, 6: 240–246. doi: 10.1002/anie.196702401
- ↑ Schulz, A. Inis, C. Klapoetke, M. (1995) Experimental and Theoretical Vibrational Studies of Covalent X-N3 Azides (X=H, F, Cl, Br, I).Application of the Density Functional Theory and Comparison with ab Initio Results Inorganic Chemistry 17, 4343-4346