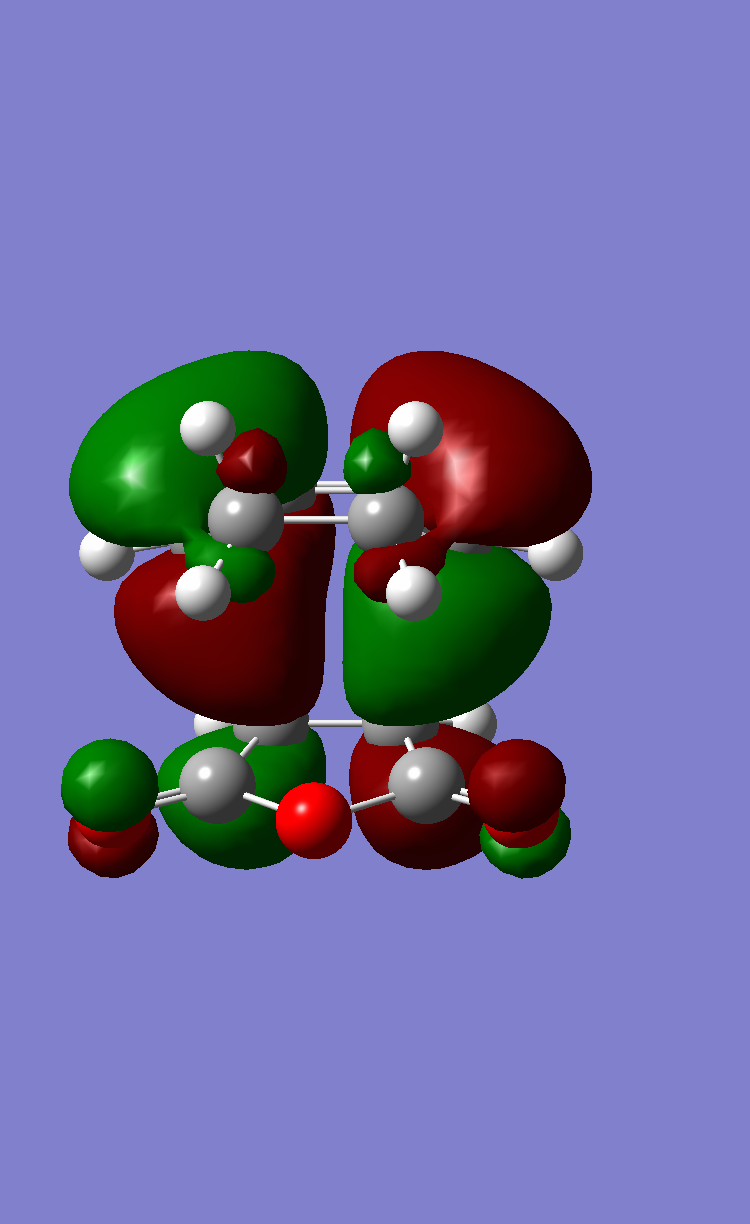
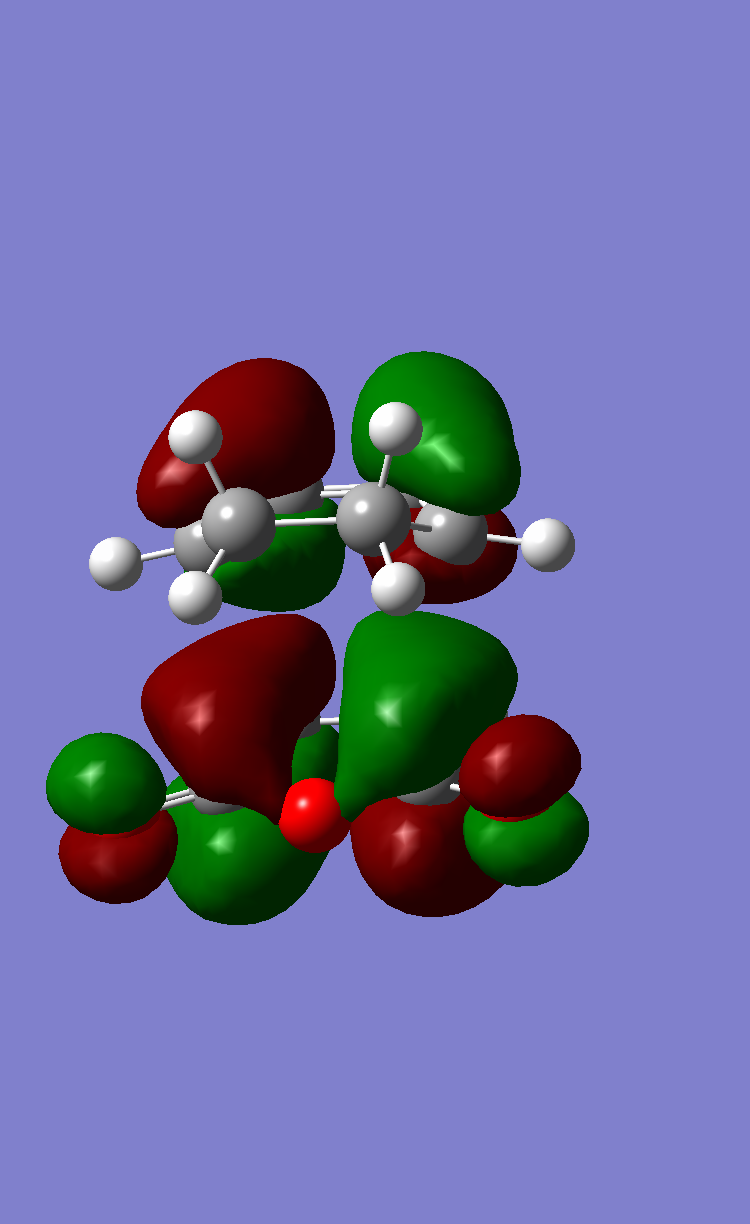
Rep:Mod:iulianamaria

Introduction

The structures and energy of the species involved in a chemical reaction offer valuable insight into the mechanism and general features of the process. Due to the advances in optimization algorithms, information about the most stable geometry, vibrational frequencies and, in principle, any observable physical quantity can be computed with a high degree of accuracy. Synthetic sequences often involve two or more reaction pathways with similar activation energies. Therefore, the location of the transition structures corresponding to each pathway on the potential energy surface is of great importance in predicting the major products.

Figure 1. Cope rearrangement reaction

The Cope rearrangement reaction of 1,5-hexadiene is an archetypal [3,3] sigmatropic shift which has been the subject of numerous theoretical and experimental studies. Computational evidence has been provided to show that the reaction can proceed via either an aromatic transition state consisting of two partially bonded three-carbon units or via a cyclohexane- 1,4-diyl-like structure. This study employs computations at the HF/3-21G and B3LYP/6-31G* levels of theory to investigate the lowest energy conformation of the reactant molecule and to locate the two possible, chair and boat, transition structures. The results are subsequently employed to rationalize the preferred mechanism and a comparison with previous research is also provided.

Figure 2. Diels-Alder cycloaddition reaction

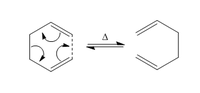
The [4+2] Diels-Alder reaction between ethylene and butadiene is another example of a process which has been extensively investigated from a theoretical and experimental point of view, but which is still not completely elucidated. Possible mechanisms that have been proposed for this reaction include a synchronous concerted approach via a cyclcic aromatic transition state, a two-stage asynchronous concerted mechanism and a stepwise process, which occurs via a stable diradical intermediate. This study uses AM1 semi-empirical molecular orbital method to locate and investigate the geometrical features of the transition state, followed by an analysis of the possible interaction between the frontier orbitals involved in the reaction. Computations at the AM1 level of theory are also employed to probe the Diels-Alder endo rule and study the possible pathways of the cycloaddition reaction between cyclohexa-1,3-diene and maleic anhydride. Both endo and exo adducts shown in Figure 2 are taken into account and their relative energies and nodal properties of the molecular oribitals are compared in order to determine the product that is preferentially formed.

Results and Computational Methods

Exercise 1. Optimizing the Reactants and Products of the Cope Rearrangement

Due to the presence of three C-C bonds and three rotational minima around each of these bonds , 1,5-hexadiene is expected to have 27 conformations in total and ten of them to be energetically distinct. The conformations shown in Figure 3 are optimized at the B3LYP/6-31G* and HF/3-21G levels of theory and their electronic energies are compared, in order to determine the lowest energy conformation of 1,6-hexadiene. Frequency calculations performed on the optimized structures at the same level of theory yielded only real and positive frequencies, confirming that a minimum was obtained. The electronic energies and symmetries, along with the sum of electronic and zero-point energies and the sum of electronic and thermal energies of the optimized structures are summarized in Table 1.

Table 1. Summary of energies (hartrees) of the conformations under investigation

Conformer	Point Group	HF/3-21G			B3LYP/6-31G*
		Electronic energy	Sum of electronic and zero-point energies (0 K)	Sum of electronic and thermal energies (298.15 K)	Electronic energy	Sum of electronic and zero-point energies (0 K)	Sum of electronic and thermal energies (298.15 K)
Anti1	C2	-231.692600	-231.539601	-231.532644	-234.611800	-234.469286	-234.461965
Anti2	Ci	-231.692535	-231.539539	-231.532565	-234.611702	-234.469212	-234.461856
Gauche3	C1	-231.692661	-231.539486	-231.532646	-234.611326	-234.468718	-234.461477

Figure 3. Anti1 (top), Gauche3 (middle) and Anti2 (bottom) conformations of 1,5-hexadiene

On the basis of conformational analysis principles, one might expect the anti1 conformation to be the lowest energy conformation of 1,5-hexadiene. However, an optimization at the HF/3-21G level of theory of the gauche3 conformation, shown in Figure 3, yields an electronic energy of -231.69266 hartrees (c.f. -231.69260 hartrees for the anti1 conformation). This suggests that, in fact, the gauche3 conformation is the global minimum.

This observation is not in accordance with the general principle that a C-C-C-C anti-periplanar arrangement enables efficient overlap between σ C-C and σ* C-C orbitals, leading to a stabilization of the filled NBO. Each C-C-C-C gauche unit has been reported to contribute 0.8-1 kcal mol^-1 to the total electronic energy of saturated aliphatic hydrocarbons such as n-butane, due to close contact between hydrogen atoms and increased bond-bond Pauli repulsion energy. . Nonetheless, the anomalous behaviour of 1,5-hexadiene can be attributed to a favourable attractive interaction between the π electrons of the C=C bonds and the nearby vinyl hydrogen atom, referred to as the CH-π interaction. However, the energy difference between the anti1 and gauche3 conformations of 0.037 kcal mol ^-1 is a tenfold smaller difference than in the case of the gauche and anti conformations of n-butane. Thus, since the Hartree-Fock Method describes only non-interacting electrons under the influence of a mean field potential and does not the include the electron correlation effects, the CH-π interaction may not be properly considered with the Hartree-Fock Method. The density functional theory optimization at the B3LYP/6-31G* level gives a higher energy difference of 0.297 kcal mol ^-1 between the gauche3 and anti1 conformations, but in this case, the gauche3 is the least stable one. The density functional theory includes the exchange-correlation energy term and thus might be expected to consider electronic effects with greater accuracy. However, the results suggest that the exchange-correlation functional used in these computations is not appropriate for the treatment of CH-π interactions. A post-Hartree-Fock Method such as the Møller–Plesset perturbation theory might have been more accurate in determining the lowest energy conformation.

The slight destabilisation of the anti2 conformation compared with the anti1 conformation can be attributed to the closer contact between one of the allylic and the terminal vinyl protons in the anti2 structure, with a distance of 2.52251 Å ( c.f. 2.52266 Å in the case of the anti1 conformer). The gauche3 conformation shows a distance of 2.61312 Å between these protons and thus reduced repulsive steric interactions, providing further evidence to support the observation that gauche3 is the lowest energy conformation of 1,5-hexadiene.

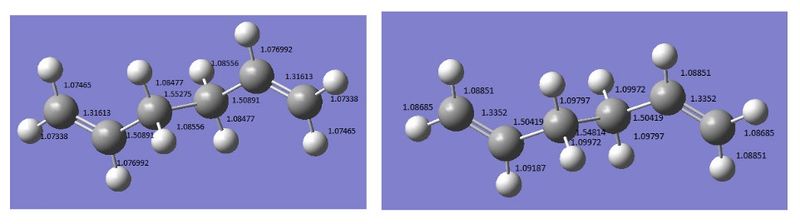
The density functional theory optimization at the B3LYP/6-31G* level of the anti2 conformation yielded a significantly lower electronic energy than in the case of the Hartree-Fock computations. Since DFT includes an approximate treatment of electron correlation, it is expected to provide more accurate results. However, in the absence of experimental data this assumption cannot be confirmed. It is worth noting that even if the overall symmetry of the optimized structure was C_i for both methods, the lengths of the C=C, C-H and C-C bonds were slightly higher when employing a DFT optimization method, as shown in Figure 4. The destabilizing interaction between occupied σ orbitals is thus diminished, resulting in a lower electronic energy. A lower electronic energy was also obtained for the DFT optimization of the other two conformations as shown in Table 1.

Figure 4. Bond distances in optimized anti2 at the HF/3-21G (left) and B3LYP/6-31G* (right) levels of theory

Exercise 2. Optimizing the "Chair" and "Boat" Transition Structures of the Cope Rearrangement

Animation 1. Normal mode with the single imaginary frequency in the chair transition structure

Two allylic fragments optimized separately at the Hartree-Fock level with a basis set of 3-21G were oriented in a chair-like conformation, with a distance between the allyl fragments of approximately 2.2 Å.The optimization to a Berny transition state of the chair transition state was performed initially at the HF/3-21G level of theory by computing the force constants at the beginning of the calculation. A vibrational analysis revealed convergence to a geometry with two imaginary vibrational frequencies and a normal mode motion which did not correspond to the desired reaction coordinate. Thus, the proposed structure was not close enough to the transition state geometry. After a basic manipulation of the position of the two allylic fragments in order to obtain a more symmetrical guess structure, the modified arrangement was re-optimized using the previous method. A single imaginary frequency of magnitude 817.94 cm^-1 and the expected normal mode motion shown in Animation 1 were obtained, confirming the successful outcome of the computation.

The same guess structure was optimized to a minimum at the HF/3-21G level of theory with the frozen coordinates method, by fixing the distance between opposite terminal allylic carbon atoms to 2.2 Å. A structure with decreased C-C bond lengths (1.381 Å c.f. 1.389 Å for the previous method) and an electronic energy of -231.619185 hartrees was obtained. The two bond/forming breaking distances were subsequently optimized using a Hessian modified to include information about the two coordinates along which the differentiation was performed. The computation gave a geometry almost identical to the one obtained by computing force constants at the beginning of the reaction, with only negligible variations of less than 0.00005 Å in both C-C and C-H bond lengths. The imaginary frequency of magnitude 817.88 was described by the same normal mode motion as for the previous method (Animation 1).

The distance between opposite terminal allylic carbon atoms and the C-C bond length were approximately 2.021 Å and 1.389 Å, respectively, for both computational methods. The resulting electronic energy and corrected energies, along with the point group of the optimized structure are summarized in Table 2.

Table2. Summary of computed energies (hartrees) for the chair and boat transition states *0 K **298.15 K

Transition state	HF/3-21G									B3LYP/6-31G*
	Force constant computation			Redundant coordinate method			QST2			Electronic energy	Sum of electronic and zero-point energies*	Sum of electronic and thermal energies**
	Electronic energy	Sum of electronic and zero-point energies*	Sum of electronic and thermal energies**	Electronic energy	Sum of electronic and zero-point energy*	Sym of electronic and thermal energies**	Electronic energy	Sum of electronic and zero-point energies*	Sum of electronic and thermal energies**
Chair (C2h)	-231.619322	-231.466697	-231.461338	-231.619322	-231.466705	-231.461345	-	-	-	-234.556932	-234.414879	-234.408950
Boat (C2v)	-	-	-	-	-	-	-231.602802	-231.450926	-231.445300	-234.543093	-234.402342	-234.396008

Figure 5. Input reactant and product geometries for the boat transition stucture computation

Animation 2. Normal mode with the single imaginary frequency in the boat transition structure

The boat transition structure was located using a QST2 approach at the HF/3-21G level, by searching for a maximum along a parabola connecting the reactant and the product, and for a minimum in all directions perpendicular to this parabola. An initial calculation was performed using the anti2 structure that was previously optimized to a minimum at the HF/3-21G level, as the reactant and the corresponding rearranged molecule. However, the calculation starting from these reactant and product structures yielded a chair transition structure with C_2h symmetry, with a distance between the central allylic carbon atoms of 2.021 Å. The geometry was thus identical to the chair structure that was previously obtained by optimization to a transition state with the Berny algorithm. (Animation 1). This shows a limitation of the QST2 method, which is not capable of locating the desired first order saddle point if the reactant and product geometries are not similar to the geometry of the boat transition structure. Therefore, the geometry of the optimized anti2 conformation was adjusted by changing the central dihedral C-C-C-C angle to 0 ^о and the angles formed by the central sp³ carbon atoms with each terminal allylic carbon atom to 100 ^о for both the reactant and the product as shown in Figure 5. Another QST2 calculation performed on the modified reactant and product structures gave a boat transition structure with an imaginary frequency of magnitude 839.87 (Animation 2). The distance between opposite terminal allylic carbon atoms was found to be approximately 2.140 Å and the C-C bond length was 1.381 Å.The resulting electronic energy and corrected energies, along with the point group of the optimized structure are summarized in Table 2.

Both optimized chair and boat transition structures at the HF/3-21G level were re-optimized using the B3LYP/6-31G* level of theory. Vibrational analysis at the same level of theory confirmed that each of the determined stationary points is a transition structure with a single negative eigenvalue at 569.16 and 530.35 cm^-1 for the chair and boat structures, respectively. The optimized chair transition structure illustrated in Figure 6 shows a distance of 1.967 Å between opposite terminal allylic carbon atoms and a C-C bond length of 1.408 Å. The optimized boat transition structure shown in Figure 7 has interallylic distance of 2.207 Å and a C-C bond length of 1.393 Å. Thus, both optimized transition structures have similar interallylic distances and C-C bond length as the structures that were previously located using the Hartee-Fock method. As noted in the previous discussion, the DFT computations yield significantly lower energies than Hartree-Fock, as a result of the inclusion of electron correlation. The breaking/forming C-C bond length for the boat transition structure is 0.240 Å longer than for the chair transition structure, which is comparable with the value of 0.230 Å found by MCSCF calculations. . The energy difference at 298.15 K between the boat and chair TS was found to be 8.12 kcal/mol, which is slightly lower than the experimental value of 11.2 ± 2.5 kcal/mol . However, these calculations at the B3LYP/6-31G* gave more accurate results than the MM2 method, which has been reported to yield an energy difference of 6.4 kcal/mol

The length of the C-C bond which are not involved in the Cope rearrangement varies between 1.381 and 1.408 Å, being comparable with a benzene C-C bond (1.40 Å). The present results suggest that the reaction proceeds via an aromatic transition state consisting of two partially bonded three-carbon units. However, this observation is not in agreement with an AM1 study which found the biradicaloid transition structure to be lower in energy than an aromatic transition state.. Thus, the preferred mechanism of the Cope rearrangement of 1,5-hexadiene is still not completely elucidated and further calculations are required to predict it.

Animation 3.Reaction coordinate in the forward direction

All calculations converged to transition structures with lengths of both C-C bonds that are forming or breaking during the rearrangement greater than a typical sp³ C-C bond, varying between 1.967 Å and 2.207 Å. Since all the pericyclic reactions that have been theoretically studied and predicted to be synchronous exhibit forming/breaking bond lengths higher than 2 Å , it is reasonable to state that computations performed at HF/3-21G and B3LYP/6-31G* levels are consistent with a synchronous mechanism for the Cope rearrangement.

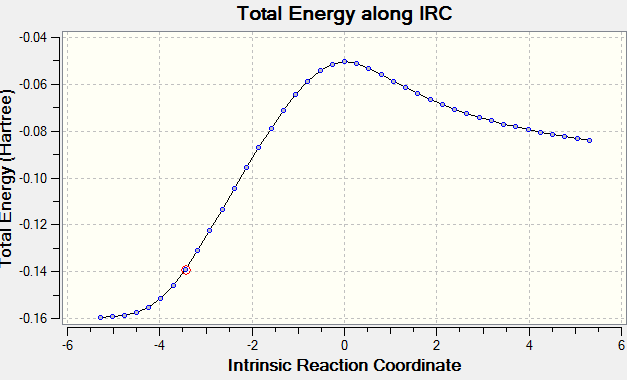
IRC computations at the HF/3-21G level provide further evidence to support this affirmation. Calculations for the rearrangement via the chair transition state converged to the structure shown in Figure 8 after 44 steps and led to a reaction profile of the type indicated in Figure 9. Since the reaction coordinate is symmetrical, computations were performed only in the forward direction. It can be observed that there are no discrete intermediates characteristic for stepwise processes and thus the reaction is concerted. The 1,5-hexadiene conformation to which the calculations converged with an electronic energy of -231.691579 hartrees was further optimized at the HF/3-21G level of theory. The C₂ symmetric gauche2 structure shown in the following figure was located as a minimum on the potential energy surface, with an electronic energy of -231.691667 hartrees. A further attempt was made to perform the IRC calculations in 100 steps, but the same configuration as the one illustrated in Figure 8 was obtained after 44 steps. Even if it would have been useful to verify that the conformation optimized at the HF/3-21G level is the correct minimum, the number of steps was not further increased due to time constraints.

Figure 9. Reaction profile in the forward direction

Figure 10. Frontier orbitals in the Cope rearrangement

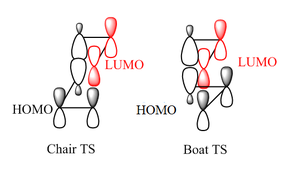
Activation energies were calculated relative to the C_i symmetric configuration of 1,5-hexadiene (anti2) for both chair and boat reaction pathways at 0 K and 298.15 K. As shown in Table 3, inclusion of electron correlation terms enhances the accuracy of the results, the computations performed at the B3LYP/6-31G* level being in reasonable agreement with the experimental values . The significantly lower activation energies for the chair pathway supports the experimental evidence that the transition structure adopts a chair-like conformation with C_2h symmetry. . A possible explanation for the preference of the chair conformation is the presence of an antibonding secondary interaction in the boat form as shown in Figure 10 (Interesting observation. Could the same type of reasoning be applied considering the interaction of the π orbitals of the two allyl fragments? João (talk) 15:59, 28 December 2014 (UTC)). By dividing the 1,5-hexadiene into an ethylene moiety and a butadiene equivalent and considering the interaction between their HOMO and LUMO, it can be noticed that in the chair transition structure, the orbitals are too far apart to exhibit significant out-of-phase overlap.

Table 3. Summary of activation energies (kcal/mol)

Activation energy	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Experimental
	0 K	298.15 K	0 K	298.15 K	0 K
ΔE (chair)	45.71	44.70	34.09	33.20	33.5 ± 0.5
ΔE (boat)	55.61	54.76	41.96	41.32	44.7 ± 2.0

Exercise 3. The Diels-Alder Cycloaddition

Cycloaddition reaction between ethene and butadiene

The AM1 semi-empirical molecular orbital method was employed to optimize to a minimum a butadiene and an ethylene fragment. The determined HOMO and LUMO for both molecules along with their symmetry with respect to the plane of symmetry shown are illustrated in Figure 11.

• Figure 11. Frontier orbitals of ethene and butadiene
• 
  Plane of symmetry
• 
  HOMO of ethene: symmetric
• 
  LUMO of ethene: anti-symmetric
• 
  HOMO of butadiene: anti-symmetric
• 
  LUMO of butadiene: symmetric

The envelope-like guess transition structure for the Diels-Alder reaction was constructed starting from a bicyclo[2.2.2]-2-octene molecule which was adjusted by removing a -CH₂-CH₂- fragment. Optimization to a transition state using the Berny algorithm at the AM1 level of theory gave a structure with an imaginary frequency of magnitude 623 cm^-1 and a normal mode which did not correspond to the desired reaction path. The initial bicyclo[2.2.2]-2-octene molecule was symmetrized and another optimization using the same method was performed. A critical point of C_s symmetry was located on the potential energy surface and vibrational analysis revealed a single imaginary vibrational frequency of magnitude 956.25 cm^-1 with the desired normal mode motion (Animation 4). The relevant optimized geometrical parameters of the envelope type transition structure are reported in Figure 12.

Figure 12. Geometrical features of the optimized transition state for the Diels-Alder reaction (Å)

Animation 4. Normal mode with the single imaginary frequency in the transition structure

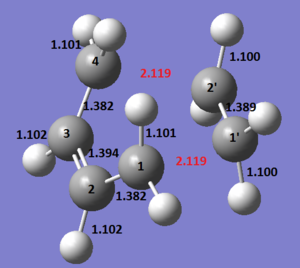
The length of the σ C-C bonds which are not involved in forming/breaking processes indicates that the reaction proceeds via a cyclic aromatic transition state. The length of the σ C-C bonds that are expected to form (2.119 Å) is greater than a typical sp³ (~ 1.54 Å) and sp² (~ 1.34 Å) bond length, but significantly lower than the sum of the corresponding van der Waals radii (~ 3.4 Å). Thus, there is a bonding interaction between the butadiene and ethylene fragments and the new σ C-C bonds are partly formed as expected for a transition structure. It has been generally reported that allowed pericyclic reactions are invariably synchronous if there are no factors which might strongly militate against synchronicity. Since concerted approaches involve cyclic aromatic transition states, the transition structures are expected to be highly symmetric based on the analogy to the structure of benzene (equal C-C bond lengths of approximately 1.40 Å). . Therefore, the equal length of both C-C bonds formed in the cycloaddition reaction suggests that the AM1 semi-empirical molecular orbital method predicts a synchronous concerted approach between cis-butadiene and ethylene. Further evidence is provided by the normal mode motion at -956.25 cm^-1 corresponding to the reaction path, which depicts a simultaneous formation of the two σ C-C bonds. The vibration with the lowest positive frequency occurs at 147.30 cm^-1 describes a nonsynchronous approach, but the motion is simply a twisting of both fragments rather than a bond forming process equivalent to the reaction path. Even if AM1 agrees with the ab initio calculation in predicting the reaction to be synchronous, MIND0/3 calculations are in favour of the process involving a stable biradicaloid intermediate, which collapses to cyclohexene in the rate-determining step. . The nature of the mechanism is thus still open to debate.

The AM1 computations can be further employed to confirm theoretical observations such as the fact that the Diels-Alder reaction is an allowed process. The Woodward-Hoffmann rule for thermal pericyclic reactions states that a ground-state pericyclic change is symmetry-allowed when the total number of (4q+2)_s and (4r)_a components is odd. "S" and "a" refer to suprafacial and antarafacial components, respectively and p and r are integers. Since the investigated Diels-Alder reaction involves only suprafacial bond formation between a diene with 4 π electrons (r=1) and a dienophile with 2 π electrons (q=0), the process can be described as having only one (4q+2)_s component and no (4r)_a components. The total number of components is thus 1 and the reaction between ethene and cis-butadiene is expected to be allowed. This is confirmed by the nodal properties of the HOMO and LUMO that were previously computed for ethene and butadiene. It is clear from Figure 13 that the overlap between HOMO of one reactant and the LUMO of the other reactant is bonding at both sites, if only suprafacial components are considered. Overlap between the HOMO of butadiene and the LUMO of ethylene gives the HOMO of the C_s transition structure, whereas interaction between the LUMO of butadiene and the HOMO of ethylene gives the LUMO of the transition structure. As shown in Figure 13, the HOMO and LUMO corresponding to the transition structure are anti-symmetric and symmetric, respectively, with respect to the plane of symmetry that was previously defined.

• Figure 13. Frontier orbitals of the TS and bonding interactions
• 
  Bonding interaction between HOMO of ethene and LUMO of butadiene
• 
  Bonding interaction between LUMO of ethene and HOMO of butadiene
• 
  HOMO of the transition structure: anti-symmetric
• 
  LUMO of the transition structure: symmetric

Figure 14.HOMO of the TS obtained at the HF/3-21G level

Note: The representation of the bonding interactions is only schematic and the relative size of the butadiene and ethene frontier orbitals is not accurate. The lines identify the bonding overlap that can develop as the reaction proceeds.

An attempt was made to perform all the above computations at the HF/3-21G level of theory. However, a transition state with the symmetric HOMO shown in Figure 14 was located, suggesting that the level of theory is not appropriate for the characterisation of the frontier orbitals involved in the Diels-Alder reaction (Or that the simple frontier orbital ideas don't exactly match the complex electronic structure of the system. João (talk) 15:59, 28 December 2014 (UTC)). Based on the remarks that were previously made for the Cope rearrangement, calculations at the B3LYP/6-31G* level might have given more accurate results. Even if the shape and the coefficients of the molecular orbitals should not have been affected, the DFT method might have given electronic and thermally corrected energies which are in better agreement with the experimental values.

Cycloaddition reaction between cyclohexa-1,3-diene and maleic anhydride

The AM1 semi-empirical molecular orbital method was employed to optimize to minimum a cyclohexa-1,3-diene and a maleic anhydride fragment. The determined HOMO and LUMO for both molecules along with their symmetry with respect to the plane shown are illustrated in Figure 15. The overlap between the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride or vice versa is bonding at both sites, if only suprafacial components are considered. The cycloaddition reaction is thus allowed, which is consistent with the predictions based on the Woodward-Hoffmann rule.

• Figure 15. Frontier orbitals of cyclohexa-1,3-diene and maleic anhydride
• 
  Plane of symmetry
• 
  HOMO of cyclohexa-1,3-diene: anti-symmetric
• 
  LUMO of cyclohexa-1,3-diene: symmetric
• 
  HOMO of maleic anhydride: symmetric
• 
  LUMO of maleic anhydride: anti-symmetric

(Is cyclohexadiene actually symmetric with respect to the vertical plane? João (talk) 15:59, 28 December 2014 (UTC))

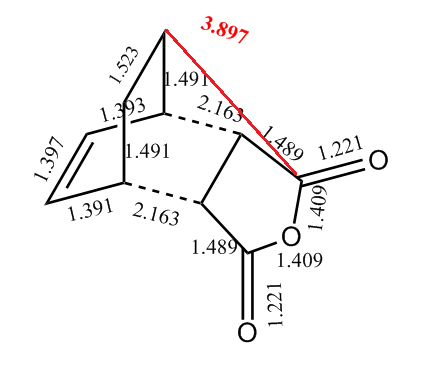
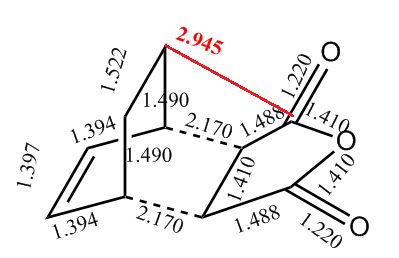
As mentioned in the introduction section, the Diels-Alder between cyclohexa-1,3-diene and maleic anhydride can give an endo or an exo adduct and thus it was necessary to construct a guess transition structure for both pathways. The guess transition structures were constructed by joining together a bicyclo[2.2.2]-2-octene molecule, adjusted as for the previous part by removing a -CH2-CH2- fragment, and a five-membered cyclic anhydride fragment, at a distance of approximately 2 Å from each other. Optimization to a transition state using the Berny algorithm at the AM1 level of theory followed by vibrational analysis gave a structure with an imaginary vibrational frequency of magnitude 806.38 and 812.02 cm^-1 for the endo and exo adducts, respectively. The desired normal mode motion (Animation 5 and 6) corresponding to the Diels-Alder reaction path was obtained in both cases. The relevant optimized geometrical parameters of both transition structures are reported in Figure 16 and 17.

Animation 4. Normal mode with the single imaginary frequency in the endo transition structure	Animation 5. Normal mode with the single imaginary frequency in the exo transition structure	Figure 16. Geometrical features of the endo transition structure	Figure 17. Geometrical features of the exo transition structure

The length of the σ C-C bonds which are not involved in forming/breaking processes is comparable with the length of aromatic C-C σ bonds, indicating that the reaction proceeds via a cyclic aromatic transition state. Analogous to the Diels-Alder reaction between ethene and cis-butadiene, the highly symmetric transition structures suggest that the AM1 semi-empirical molecular orbital method predicts a synchronous concerted approach between cyclohexa-1,3-diene and maleic anhydride via both endo and exo adducts.. Further evidence is provided by the normal mode motion at the imaginary frequency, which depicts a simultaneous formation of the two σ C-C bonds for both transition structures. In addition, IRC calculations at the AM1 level of theory, performed in both directions in 20 steps, are consistent with the proposed synchronous mechanism. The reaction profile does not show any discrete intermediates characteristic for stepwise processes, excluding thus the possibility of a mechanism proceeding via biradical or zwitterionic intermediates. It should be noted that the in the case of the IRC computation via the endo transition structure, the first step on the reaction path corresponds to the reactants and the last step corresponds to the cycloaddition product, whereas in the case of the exo transition structure the opposite situation was observed. Thus the IRC computations performed at the AM1 level confirm the exothermic nature of the Diels-Alder cycloaddition reaction.

Figure 18. Reaction profile via the endo transition structure

Figure 19. Reaction profile via the exo transition structure

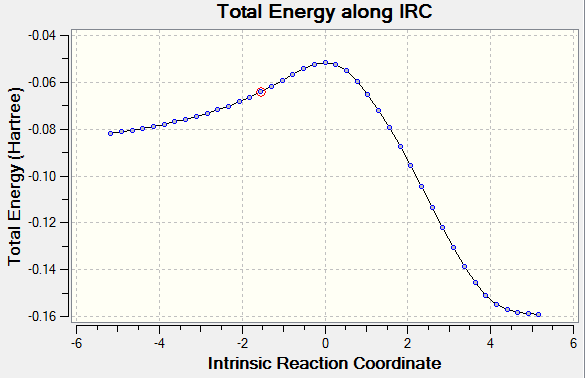
The computed electronic and thermally corrected energies of the endo and exo transition structures are reported in Table 4 below. The calculations suggest that the activation energy of the reaction pathway which proceeds via the endo transition structure is lower than the activation energy of the process involving the exo transition structure by 0.87 kcal/mol (0.0013185 hartrees) at 0 K and 0.75 kcal/mol (0.001197 hartrees) at 298.15 K. Therefore, the AM1 predictions are in agreement with the experimental observation that the Diels-Alder reaction between maleic anhydride and cyclohexa-1,3-diene gives the endo product faster than it gives the exo adduct, even though the latter is thermodynamically more stable.

Table 4. Summary of computed energies (hartrees) for the endo and exo transition states

Optimized molecule	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
Cyclohexa-1,3-diene	0.027711	0.152502	0.157726
Maleic anhydride	-0.121824	-0.063346	-0.058192
Endo TS	-0.051505	0.133494	0.143683
Exo TS	-0.050419	0.134879	0.144880

Figure 20. Secondary orbital interaction in the endo transition structure

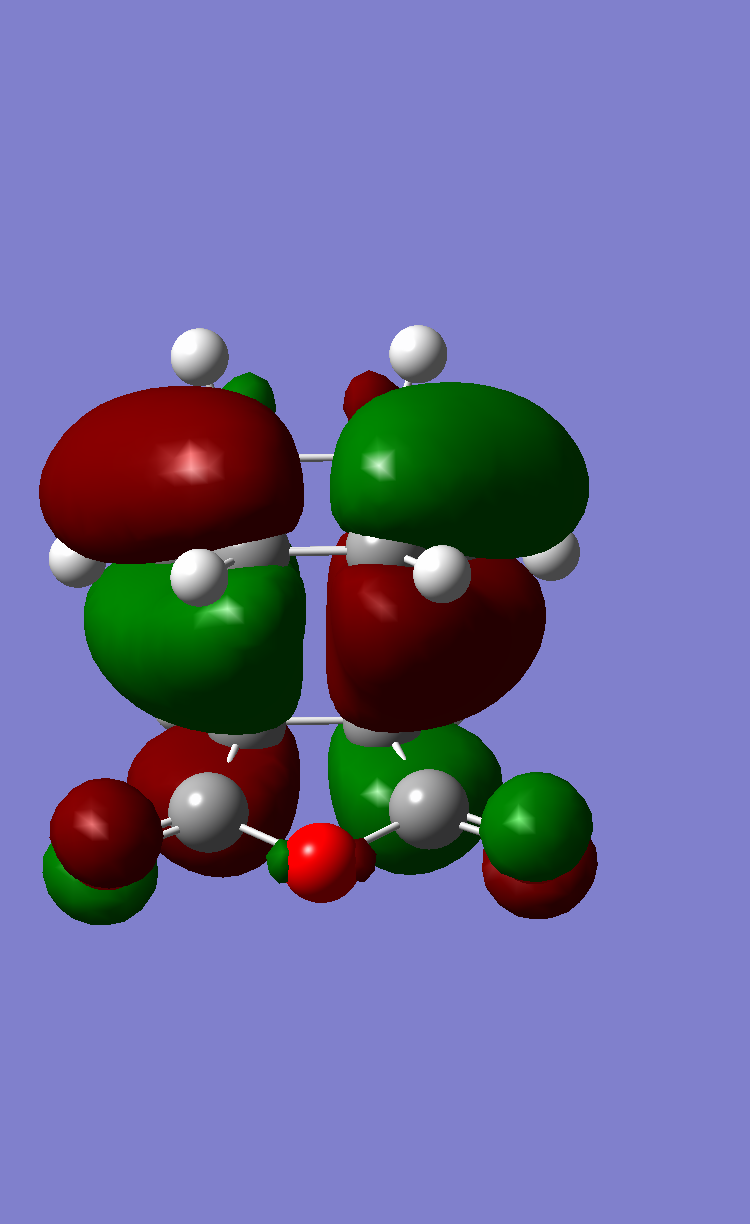
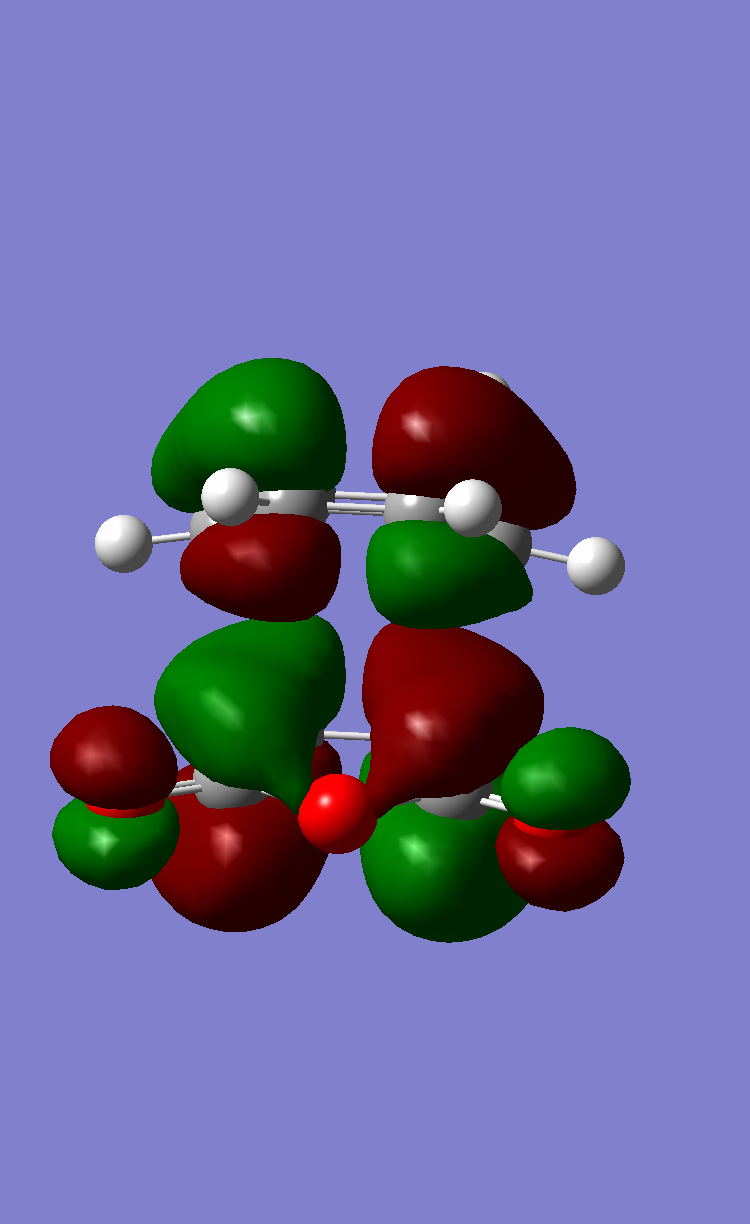
In order to account for the formation of the endo adduct under kinetically controlled conditions, the nodal properties of the frontier orbitals of the reactants and both transition structures were examined. The interaction between the frontier orbitals can be simplified in a diagram involving only atomic orbitals (Figure 20). It can be clearly observed that the endo transition structure is characterized by an in-phase secondary overlap between the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride (Do you actually see evidence of this in your calculated orbitals? João (talk) 15:59, 28 December 2014 (UTC)). Since this stabilising secondary orbital interaction is not possible for an exo adduct, the endo transition state is expected to be lowered in energy relative to the exo one. The stabilisation of the endo transition state is further reinforced by the increased C-C through space distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the carbon atoms of cyclohexa-1,3-diene which are not involved in the reaction (3.897 Å c.f. 2.945 Å in the exo adduct (This is not a completely fair comparison as for endo you are measuring a distance to the opposite side of the molecule. João (talk) 15:59, 28 December 2014 (UTC))), which indicates diminished steric repulsion.

Figure 21. HOMO of the endo transition structure: anti-symmetric	Figure 22. LUMO of the endo transition structure: anti-symmetric	Figure 23. HOMO of the exo transition structure: anti-symmetric	Figure 24. LUMO of the exo transition structure: anti-symmetric

The computations performed for the cycloaddtion reaction between butadiene and ethene demonstrated that the AM1 method provides more accurate results than Hartree-Fock, since it implicitly takes into account electronic correlation through the use parameters derived from experimental data. However, as any other semi-empirical method, it is expected to give very reliable results only for systems which are related to those from which their parameters have been fitted. A further study might involve the use of MCSCF calculations, which have been reported to give a more a balanced description of closed-shell species.

Conclusions

Hartree-Fock calculations with a basis set of 3-21G were employed to determine the lowest energy conformation of 1,5-hexadiene, which was found to be the gauche3 structure. The density functional theory optimization at the B3LYP/6-31G* level did not confirm this result, suggesting a poor choice of the exchange-correlation functional for the treatment of CH-π interactions (Or revealing the the lowest energy structure is actually anti? João (talk) 15:59, 28 December 2014 (UTC)). All the computations performed at the HF/3-21G and B3LYP/6-31G* levels were consistent with a synchronous mechanism for the Cope rearrangement. DFT calculations gave an energy difference at 298.15 K between the boat and chair transition structures of 8.12 kcal/mol, indicating that the transition structure adopts a chair-like conformation with C2h symmetry.

The AM1 semi-empirical molecular orbital method provided evidence that the Diels-Alder reaction between ethene and butadiene is an allowed process, which proceeds via a cyclic aromatic transition state, with simultaneous formation of the two σ C-C bonds. In contrast, the HF/3-21G level of theory failed in predicting the symmetry of the frontier orbitals of the transition state.

The endo rule in Diels-Alder reactions was successfully investigated for the cycloaddition reaction between cyclohexa-1,3-diene and maleic anhydride. The activation energy of the reaction pathway which proceeds via the endo transition structure was found to be lower than the activation energy of the process involving the exo transition structure by 0.87 kcal/mol at 0 K and 0.75 kcal/mol at 298.15 K. AM1 computations predict a synchronous concerted approach between cyclohexa-1,3-diene and maleic anhydride via both endo and exo adducts.