Rep:Mod:intersect

Cope Rearrangement

The cope rearrangment is a [3,3] Sigmatropic pericyclic reaction. It is generally accepted that the reaction occurs in a concerted manner, during which one σ bond is broken while another is formed simultaneously, via a transition state with either a "chair" or "boat" geometry ("chair" transition structure typically more energetically favourable) resulting in the concerted migration of a group from one point of attachment to a conjugated system to another point of attachment.

In this exercise, molecular orbital-based methods were used to find the minimum-energy conformation and transition structures on the 1,5-hexadiene potential energy surface in order to predict the preferred reaction mechanism. The Schrodinger equation must be solved numerically and the molecular orbitals computed (to observe changes in electron distribution) in order to describe bond making and breaking processes(information on the transition state structure and energy). This is important as the reaction mechanism(transition state structures) depends highly on the orbital symmetry and overlap of reactants. Finally, Intrinsic reaction coordinate (IRC) was used to relate the starting material/final product comformation to the transitions State.

Optimisation of reactants and products

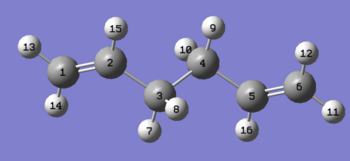
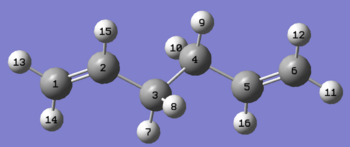
Conformers of 1,5-hexadiene

Optimisation with HF/3-21G

The structures of several conformers of 1,5-hexadiene were optimised by using HF/3-21G level. The symmetry was determined by using the Symmetrize option in Gaussview.

Conformers of 1,5-hexadiene and their relative energies

Conformers of 1,5-hexadiene and their relative energies

Conformer	structure	Energy /a.u. (HF/3-21G)	Relative Energy /kcal mol-1	Point Group
anti 1	anti1	-231.69260	0.04	C2
anti 2	anti2	-231.69254	0.08	Ci
gauche 1	gauche1	-231.68772	3.10	C2
gauche 2	gauche3	-231.69167	0.62	C2
gauche 3	gauche3	-231.69266	0.00	C2

data for anti 1 :Media:ANTI MOLNEW2.LOG‎ data for anti 2 :Media:ANTI MOLNEW1.LOG data for gauche 1 :Media:GAU WU1.LOG data for gauche 2 :Media:GAU MOLNEW1.LOG‎ data for gauche 3 :Media:GAU WU3.LOG‎

The gauche conformers are expected to be less stable than the anti conformers due to more steric repulsions. However, the gauche3 conformer is the most stable of all the conformers optimised. This is due to stereoelectronic effect involving stabilising interaction between the π-electrons of the C=C and vinyl protons(C-H σ* - C=C π orbital overlap), otherwise known as CH-π interaction. This is in agreement with Literature reported by Rocque et al .

Optimisation of Anti2-Conformer with DFT/B3LYP/6-31G(d)

Comparison between HF/3-21G and DFT/B3LYP/6-31G(d) Optimisation

The Anti2 conformer was optimised at the B3LYP/6-31G level. A summary and comparison of both methods (HF/3-21G and DFT/B3LYP/6-31G*) are shown:

Comparison of optimisation properties of anti2 conformer, by different methods

Method	HF/ 3-21G	DFT/ B3LYP/ 6-31G*
Geometry
Structure
Point Group	Ci	Ci
Energy/ a.u.	-231.69254	-234.61170
Bond length C1=C2, C5=C6 / Å	1.32	1.33
Bond length C2-C3, C4-C5 / Å	1.51	1.50
Bond length C3-C4 / Å	1.55	1.55
Dihedral angle C1-C2-C3-C4 /o	114.7	118.6
Dihedral angle C2-C3-C4-C5 /o	180.0	180.0
Dihedral angle C3-C4-C5-C6 /o	-114.7	-118.6

data for DFT : Media:ANTI CORRECT B3LYP.LOG‎

The results show the final energy calculated by DFT is lower than that by HF, the geometry calculated show the C=C bond length is slightly(0.1Å) larger(smaller bond order) in the DFT optimised structure suggesting the atoms are more spread out reducing steric repulsions which could possibly account for the lower energy. Also, the dihedral angle between the 4 terminal carbons was larger(4^o) for the DFT calculations.

Thermochemistry of Anti-2 conformer

The thermochemistry information was obtained by carrying out a frequency calculation on the optimised structure, at the same level of theory DFT/B3LYP/6-31G*. This gives information about the vibrational energies and various contribution and correction terms. These parameters are temperature-dependent so the calculation was performed at 0K and 298.15K and no imaginary frequency was observed.

Comparison of thermochemistry of anti1 conformer at different temperatures

Energies	At 0 K	At 298.15 K
Sum of Electronic and Zero-point Energies / a.u.	-234.46877	-234.46920
Sum of Electronic and Thermal Energies / a.u.	-234.46143	-234.46186
Sum of Electronic and Thermal Enthalpies / a.u.	-234.46049	-234.46091
Sum of Electronic and Thermal Free Energies / a.u.	-234.50037	-234.50078

data for 0K: DOI:10042/to-7193

The Sum of electronic and zero-point Energies is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE).

The Sum of electronic and thermal Energies is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + Evib + Erot + Etrans).

The Sum of electronic and thermal Enthalpies contains an extra correction for RT (H = E + RT), which is particularly important when looking at dissociation reactions.

The Sum of electronic and thermal Free Energies includes the entropic contribution to the free energy (G = H - TS).

The results show the calculated energies are lower at 0K than at 298.15K. This is expected since at higher temperature, the system has higher energy due to higher translational, rotational and vibrational modes. The last term is most negative as the entropic contribution is taken into account.

Optimisation of transition state structures

The transition state(chair or boat) of the Cope Rearrangement can be modelled and investigated in using Computational Modelling

Optimisation of Chair transition state

The chair transition state was optimised using two different methods, both at the level of theory of HF/3-21G (at default temperature of 198.15K and 1.0atm pressure):

1.TS (Berny) method, optimisation using TS(Berny) directly by calculating the force constant(once) at the beginning of the optimisation. This method is very sensitive to the structure of the input, therefore the approximate structure for the transition state needs to be accurate to optimise to the correct TS. It works by computing the force constant matrix (Hessian) in the first optimisation step and then constantly recalculated as the optimisation proceeds.

2.Frozen Coordinate method, by using the redundant coordinate editor to set breaking/forming bond to 2.2Å and optimise it to a minimum, and subsequently use Bond Derivative(release fixed bond length) and optimise using TS(Berny) without computing the force constants. This methods differentiates along the reaction coordinate and it is not necessary to compute the whole Hessian. A reasonable estimation of the terminal distance between the allyl fragments must be known.

Comparison of Optimisation of Chair- Transition State with Different Conditions

	TS (Berny) method	Frozen Coordinate method
structure	anti1	anti1
point group	C2h	C2h
Optimised Energy/a.u.	-231.61932	-231.61932
Bond forming length/Å	2.02	2.02
Bond breaking length/Å	2.02	2.02
Imaginary Vibrational Frequency/cm-1	-818	-818
Vibration

data for TS (Berny) method: Media:CHAIR TS OPT wu.LOG‎
data for Frozen Coordinate method: Media:Wu PART D.LOG‎

The results show both methods gave very similar outcomes(the differences are not significant considering the accuracy of Gaussian), suggesting either method is reliable and sufficient.

The vibrational mode at the imaginary frequency -818cm^-1 shows the vibration of the transition state, it can be seen that the bond breaking/ bond forming motions occur in a concerted manner simultaneously and asynchronously (one bond breaks while the other forms). This corresponds to the concerted reaction involved in the [3,3]-sigmatropic pericyclic cope rearrangement.

Optimisation of Boat transition state

The boat transition state was optimised using QST2 at the same level of theory. In this method, the reactant and product for the reaction were specified, and then the calculation interpolates between the two structures to find a transition state between them. The geometry of both the product and reactant structure have to be specified very close to that of the boat transition state, when they are not drawn correctly(or not close enough) the calculation will not be able to interpolate between them and fail(demonstrated during first optimisation). The geometry was modified so that the central C-C-C-C dihedral angle was changed to 0^o and the inside C-C-C angles to 100^o for both molecules. The calculation was able to predict the boat transition state after modification.

Optimising boat transition state using QST2

	QST2
Structure	anti1
Point group	C2v
Energy/ a.u.	-231.60280
Bond Forming & Breaking Length/ Å	2.14
Imaginary Vibrational Frequency/ cm-1	-840
Vibration

data : DOI:10042/to-7176

The results show the energy of the boat(eclipsed conformation) transition state is higher compared to the chair(staggered conformation, minimal steric repulsion), this is due to greater steric repulsion(higher torsional strain between the eclipsed carbons and hydrogens) in the boat structure. This would also suggest that the boat transition state has a higher activation energy than the chair transition state(confirmed by activation energy analysis below).

Similar to the chair TS, the vibrational mode at the imaginary frequency -840cm^-1 shows the vibration of the transition state( concerted bond-forming/breaking process) corresponding to the concerted reaction involved in the [3,3]-sigmatropic pericyclic cope rearrangement.

Intrinsic Reaction Coordinate (IRC) of Chair transition state

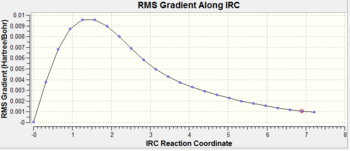
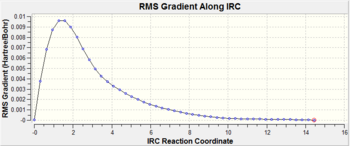
The Intrinsic Reaction Coordinate (IRC) was calculated for the chair transition state (from TS(Berny) with frozen coordinates method) to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. The reaction coordinate was computed in the forward direction, using 50 points along the IRC. An initial calculation was performed with the force constant computed only once but the calculation had not yet reached a minimum geometry. Another calculation was done with 50 points, with the force constant calculated at every point.

Comparison of IRC results for Chair-TS

Force Constant Computation	minimum geometry reached	Energy/a.u.	Total energy along IRC Path	Gradient along IRC Path	Minimum Structure
Once	no	-231.68810		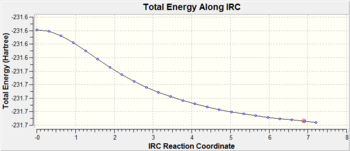	anti1
Always	yes	-231.69166		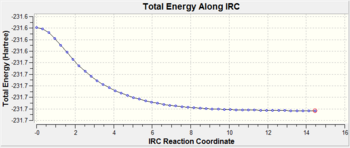	anti1

data for once :DOI:10042/to-7174 data for always: DOI:10042/to-7175

For the IRC to be successful, the energy of the system should plateau to a minimum with a RMS gradient close to zero showing the minimum geometry has been found. The IRC path when force constant computed = once, shows the energy is decreasing(yet to plateau) and RMS gradient is also decreasing(yet to reach zero). In order found the minimum geometry, the number of points could be increased(calculation continues to decrease along IRC path) or the force constant can be computed at every point. The above results show when the force constant computed = always, the IRC path plateated to a minimum with the RMS gradient decreasing to zero. Therefore, this successful calculation can be related to the gauche2 conformer , which has an energy of -231.69167 a.u.

Activation energies for the transition states

The HF/3-21G optimised chair and boat transition structures were optimised again using a higher (more complex) level of theory, DFT/B3LYP/6-31G. Frequency calculations were carried out to calculated and compare the activation energies for the reaction via both transition structures. The values are also computed at 0K and at 298.15K.

summary of energies of Chair & Boat TS at 0K & 298.15K

	B3LYP/6-31G*
	Electronic energy/a.u.	Sum of electronic and zero-point energies/a.u.	Sum of electronic and thermal energies/a.u.
		at 0 K	at 298.15 K
Chair TS	-234.556983	-234.414929	-234.409008
Boat TS	-234.543093	-234.402340	-234.396005
Reactant (anti2)	-234.611710	-234.469204	-234.461857

data for chair-TS by B3LYP: DOI:10042/to-7130 data for boat-TS by B3LYP: DOI:10042/to-7177

The results show the more complex basis set produced lower energies values, this is expected as the larger basis set is more accurate.

The activation energies (ΔE) for the transition state at 0K can be found by calculating the difference between the sum of electronic & zero-point energies of reactant anti2 1,5-hexadiene and the chair/boat transition state. E(A) for TS at T=298.15K is found by the difference between the sum of electronic & thermal energies

Comparison of Activation Energies of Chair & Boat TS at 0K & 298.15K

	B3LYP/6-31G*				Experimental Value
	at 0K/a.u.	at 0K/kcal mol-1	at 298.15K/a.u	at 298.15K/kcal mol-1	at 0K/kcal mol-1
ΔE (Chair TS)	0.0543	34.07	0.0528	33.13	33.5 ± 0.5
ΔE (Boat TS)	0.0668	41.92	0.0659	41.35	44.7 ± 2.0

Units for ΔE was converted from Hartree to kcal/mol (1 hartree = 627.509 kcal/mol)

The activation energy ΔE is found to be always higher for the boat conformation compared to the chair, this is in agreement with the chair TS being more stable than the boat TS. Therefore, the chair TS is the expected TS for the Cope Rearrangement of 1,5-hexadiene, With the anti 2 conformr as the reactant and the gauche 3 conformer as the product.

The activation energies calculated using DFT/B3LYP/6-31G corresponds better with experimental values. The calculated results for the chair TS relates very well with experimental while experimental value is higher than that calculated for the boat TS.

Diels Alder Cycloaddition

The Diels-Alder reaction is a [4+2] pericyclic cycloaddition, between a conjugated diene and a dienophile involving the concerted formation of two (or more) σ-bonds between the termini of two or more conjugated π-systems.

Two reactions were investigated:

1. cis-butadiene and ethylene

2. 1,3-cyclohexadiene and maleic anhydride

The number of π-electrons involved in the pericyclic transition state determines whether the reaction will proceed in a concerted stereospecific fashion (allowed) or not (forbidden). Both reactions are thermally allowed by the pericyclic selection rules as they involve 6 π electron and will proceed via a Huckel transition state will all suprafacial components.

cis-Butadiene and Ethylene

Cis-butadiene and ethene react together in a Diels-Alder reaction:

Molecular Orbitals of reactants

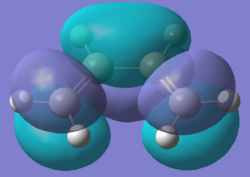
The structures of the reactants cis-butadiene and ethylene were optimised using Semi-Empirical/AM1 method. The HOMOs and LUMOs for the two molecules were also calculated. The symmetry of the molecular orbitals can be determined by looking at whether there is a plane of reflection in the centre of the molecule.

HOMO and LUMO of cis-butadiene and ethene

	cis-Butadiene		Ethylene
	HOMO	LUMO	HOMO	LUMO
Molecular Orbital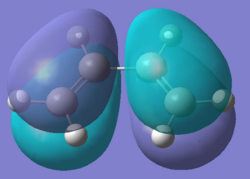
Energy / a.u.	-0.34383	0.01709	-0.38774	0.05285
Symmetry	Antisymmetric	Symmetric	Symmetric	Antisymmetric

data for cis-Butadiene: DOI:10042/to-7171 data for Ethylene: DOI:10042/to-7172

The MOs show the symmetries for the HOMO and LUMO orbitals for ethylene are the opposite to those for cis-butadiene(HOMO of ethylene and LUMO of butadiene are symmetric while LUMO of ethylene and HOMO of butadiene are asymmetric). Therefore due to MO theory(HOMO-LUMO interactions must have same symmetry), the HOMO-LUMO orbital pairs that interact are the HOMO of cis-butadiene and the LUMO of ethene and the LUMO of cis-butadiene and the HOMO of ethylene. These interactions results the formation of 2 σ bonds in an "allowed" Diels Alder cycloaddition.

Orbital symmetry is important in pericyclic reactions as it determines whether the reaction will proceed and it's stereochemical outcome.

Transition State

Optimisation

The transition state of the Diels Alder reaction was optimised using the Frozen Coordinates method, first freezing the bond to 2.1Å and optimised to a minimum, followed by bond derivative and optimising to TS(Berny). The calculation was performed using Semi-Empirical/AM1 method.

Optimisation of transition state

	Frozen Coordinate Method
structure	anti1
Point Group	Cs
Energy/ a.u.	0.11166
Bond forming Length/ Å	2.12
Bond breaking Length/ Å	2.12
Imaginary frequency/ cm-1	-957

data : DOI:10042/to-7173

An imaginary frequency was observed indicating the transition state was successfully found.

Geometry

The optimised geometry of the transition state was investigated further and compared to typical literature values of bond lengths:

Geometry of optimised transition state

	Frozen Coordinate Method
Geometry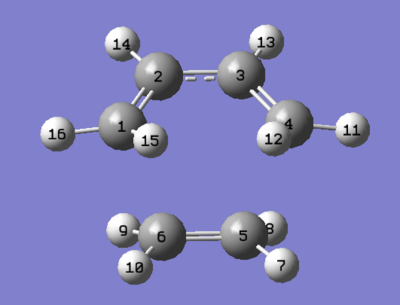
Bond Length C1-C2 / Å	1.38
Bond Length C2-C3 / Å	1.40
Bond Length C3-C4 / Å	1.38
Bond Length C5-C6 / Å	1.38
Bond Forming or Breaking length C4-C5/ Å	2.12
Bond Forming or Breaking length C6-C1 / Å	2.12
Angle C3-C4-C5 & C2-C1-C6/o	99.4
Angle C4-C5-C6 & C1-C6-C5/o	109.9
Angle C1-C2-C3 & C4-C3-C2/o	121.1

Literature values

	Literature values ,
sp3 C-C Bond Length/ Å	1.544
sp2 C-C Bond Length/ Å	1.338
Van der Waals radius of Carbon/ Å	1.70

The C-C bond length of the partially formed σ C-C bonds(2.12Å) is longer than the typical sp³ C-C bond length but horter than twice the van der waals radius of carbon. This suggests that the C-C bond is in the process of forming(bonding/overlap present), but it is not yet a full C-C bond. Moreover, the sp² C=C bond lengths of 1.38Å and sp³ C-C bond Length of 1.40Å in the optimised TS molecules suggests the π-bonds are breaking to form C-C bonds and a π-bond is forming between the two sp³ carbons.

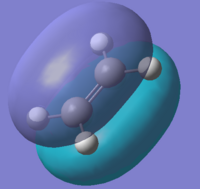
Molecular Orbitals

The HOMO and LUMO orbitals of the transition states were visualised

HOMO and LUMO of transition state

	HOMO	LUMO
Molecular Orbital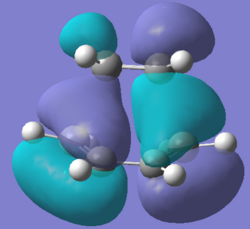
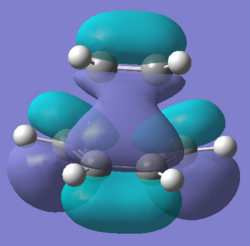
Energy / a.u.	-0.32396	0.02320
Symmetry	Antisymmetric	Symmetric

The HOMO of the transition state is antisymmetric as it is made up of the antisymmetric HOMO (п) of cis-butadiene and the antisymmetric LUMO (п*) of ethylene, this is consistent with conservation of orbital symmetry(symmetry of an orbital formed by the overlap of two orbitals must be the same as the symmetry of the initial orbitals). The orbitals involved are typical of cycloaddition reactions, where the HOMO of the diene interacts with the LUMO of the dienophile. The pericyclic reaction selection rules(under thermal conditions) states that a pericyclic reaction involving 4n+2 electrons would result in a product with suprafacial stereochemistry via a Huckel aromatic transition state. This Diels Alder reaction involves 6п (4n+2) electrons and the bond forms over the same face of the butadiene п system (suprafacial) and also over the same face of the ethene п system (suprafacial), therefore the reaction is allowed as it follows the pericyclic selection rules.

Vibrational frequency

The imaginary frequency and lowest real vibration are shown :

Vibrations of Transition State

Frequency/cm-1	Description	Mode of Vibration
-957	Synchronous formation of bonds - carbon atoms on ethylene and butadiene move toward each other in a concerted motion forming two σ bonds.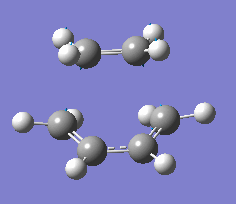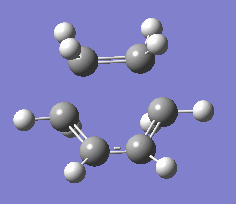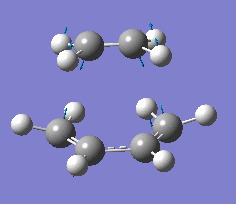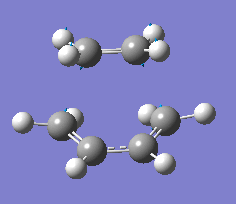
148	Rocking- ethene unit rocks with slightly larger amplitude compared to butadiene unit.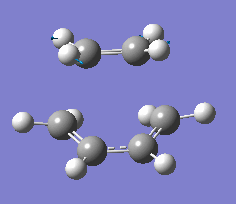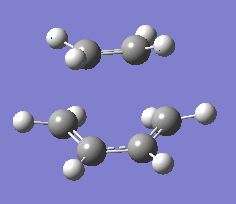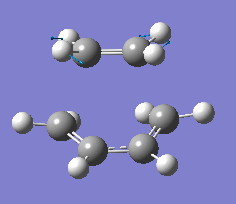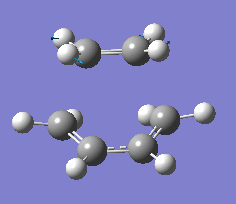

The vibrational mode at the imaginary frequency -957cm^-1 shows the vibration of the transition state, the vibration shows the synchronous formation of two new σ C-C bonds between the termini of the two molecules. This corresponds to the [4+2] pericyclic cycloaddition (Diels-Alder reaction) involving the concerted formation of two σ bonds.

Activation energy

The transition structures were reoptimised with a higher level of theory, DFT/B3LYP/6-31G(d), and the results obtained at the two different levels of theory is shown. The activation energies ΔE were found by calculating the difference between the sum of electronic and Thermal Energies of the reactants(combined) and the transition state.

Summary of energies

	AM1			B3LYP/6-31G*
	Electronic Energy/a.u.	Sum of electronic & thermal energies/a.u. at 298.15K	Activation Energy ΔE /kcal mol-1	Electronic Energy/a.u.	Sum of electronic & thermal energies/a.u. at 298.15K	Activation Energy ΔE /kcal mol-1
sum of Reactants (Cis-Butadiene+Ethene)	0.07499	0.21511	27.82	-234.52586	-234.41422	20.53
Transition State	0.11165	0.25945		-234.54395	-234.42962

Units for ΔE was converted from Hartree to kcal/mol (1 hartree = 627.509 kcal/mol)

data for TS by AM1 : DOI:10042/to-7173 data for cis-butadiene by AM1 : DOI:10042/to-7171 data for ethylene by AM1 : DOI:10042/to-7172

data for TS by B3LYP/6-31G* : DOI:10042/to-7132 data for cis-butadiene by B3LYP/6-31G* : DOI:10042/to-7135 data for ethylene by B3LYP/6-31G* : DOI:10042/to-7134

The energies found using the DFT calculations are very different compared to the ones obtained from AM1, the absolute value of the energy is meaningless and only the difference in energies is physically observable.

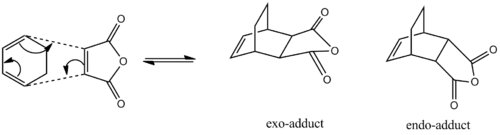
Cycloaddition of Cyclohexa-1,3-diene and Maleic Anhydride

The reaction between cyclohexa-1,3-diene and Maleic Anhydride is a Diels-Alder reaction resulting in two potential products, the exo and the endo product.

The endo and exo products are diastereomers, the direction of attack by the diene (cyclohexa-1,3-diene) on the dienophile (Maleic Anhydride) determines which isomer is formed. The endo isomer is the major product of the reaction as endo-products are formed faster(kinetic product) due to transition state stabilisation and therefore lowered activation energy . Calculations were performed to predict and explain this stereoselectivity.

Transition State

Optimisation of the exo and endo transition states

The reactants (1,3-cyclohexadiene and maleic anhydride) were first optimised using the Semi-Empirical AM1 method. The transition structures for the endo and exo products were then optimised, using TS(Berny)at the Semi-Empirical/AM1 level of theory and subsequently at a higher level of theory of DFT/B3LYP/6-31G*. Calculations were performed using the frozen coordinates method.

Comparison of optimisation of transition states

	Exo TS		Endo TS
	AM1	B3LYP/6-31G*	AM1	B3LYP/6-31G*
structure	anti1	anti1	anti1	anti1
Energy/ a.u.	-0.05042	-612.69149	-0.05150	-612.69723
Sum of electronic and thermal energies / a.u.	0.14488	-612.50010	0.14368	-612.505861
Imaginary Frequency/ cm-1	-811	-448	-806	-446
Vibration

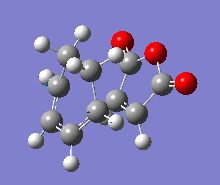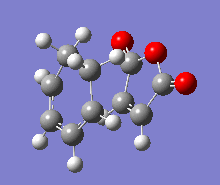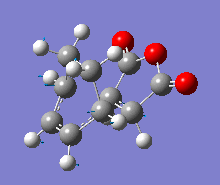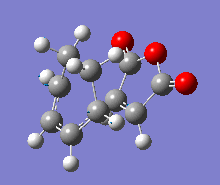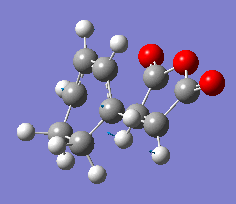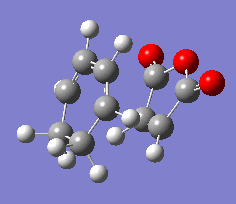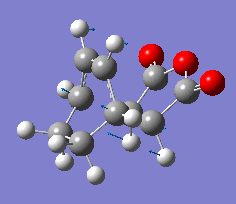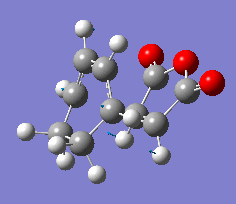data for exo-TS by AM1: DOI:10042/to-7152 data for endo-TS by AM1: DOI:10042/to-7153
data for exo-TS by B3LYP/6-31G*: DOI:10042/to-7154 data for endo-TS by B3LYP/6-31G*: DOI:10042/to-7158

The results show endo transition state is thermodynamically more stable (lower in energy) compared to the exo transition state suggesting the endo transition state is favoured(lower transition state energy results in reduced activation energy and formation of kinetic product).

The presence of one imaginary frequency confirms that the optimised structure is a transition state. The imaginary frequencies of exo and endo states show that the bond formation(in TS) occurs in a concerted, synchronous manner corresponding to the [4+2] pericyclic cycloaddition (Diels-Alder reaction).

Geometry

The geometry of the endo and exo TS found at the DFT/B3LYP/6-31G* level of theory are shown, important bond lengths including the partly formed σ C-C bonds and C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- for the exo and the “opposite” -CH=CH- for the endo were obtained along with other C-C distances.

Geometry of Exo and Endo Transition States

	Exo TS	Endo TS
Geometry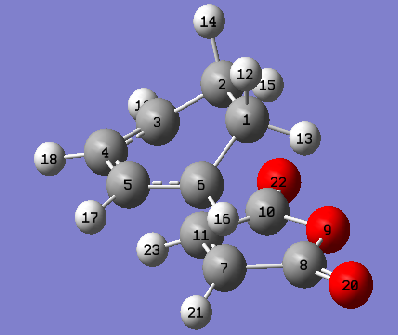
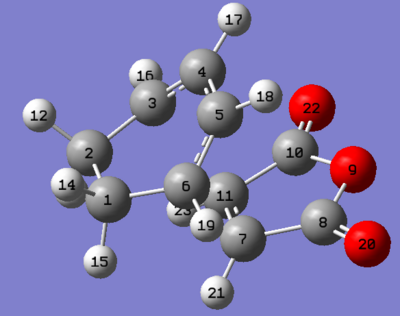
Bonds(σ) forming length C3-C11 & C6-C7/ Å	2.30	2.27
secondary orbital overlap length C4-C10 & C5-C8/ Å	3.87	2.99
Bonds length C1-C2/ Å	1.56	1.56
Bonds length C2-C3 & C1-C6/ Å	1.51	1.51
Bonds length C4-C5 / Å	1.40	1.40
Bonds length C3-C4 & C6-C5/ Å	1.39	1.39
Bonds length C7-C11 / Å	1.40	1.40
Bonds length C11-C10 & C7-C8 / Å	1.47	1.47
Bonds length C10-C19 & C8-C9 / Å	1.40	1.40

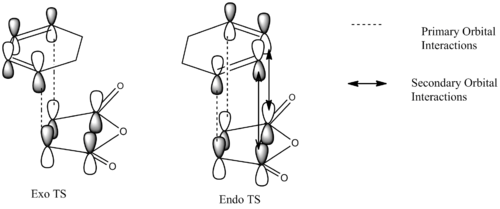
The results show all the non-through space bond length are similar between the two TS structures. The bond forming/breaking length are also similar for the TS structures. The steric repulsion in the endo TS is greater compared to the exo due to the 1,3-diaxial compression being present in the endo between the sp³ hydrogens at the back of the cyclohexen ring and hydrogens of the maleic anhydride. However the endo TS has a lower energy compared to the exo, this can be attributed to the secondary orbital interactions present only in the endo isomer (shown in molecular orbitals discussion below), the bond length for possible secondary orbital overlap length is much smaller for the endo(2.99Å) compared to the exo(3.87Å).

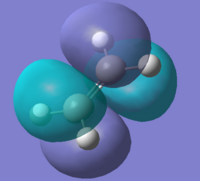
Molecular Orbitals

The primary and secondary orbital interactions involved in the Diels Alder cycloaddition reaction between 1,3-hexadiene and maleic anhydride can be described by the digram below, it is similar to that reported by Imade et. al. (cycloaddition of cyclopropene to butadiene).

The favourable secondary orbital overlap is present in the endo TS between the anhydride and diene at a distance of 2.99Å. This is not present in the exo TS as the distance(3.87Å) between the fragments is two far for effective overlap between the orbitals. Secondary orbital overlap is the interaction between the in-phase orbitals on the central carbons of the conjugated π-system in the cyclo-1,3-hexadiene fragment and the π*-orbital of the C=O bonds from the maleic anhydride fragment.

The key molecular orbitals of the exo and endo transition states obtained at the DFT/B3LYP/6-31G* level of theory were visualised and investigated.

Molecular Orbitals of Exo transition state

	HOMO	LUMO
Molecular Orbital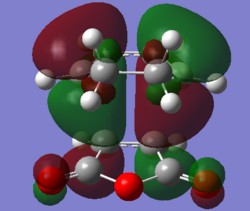
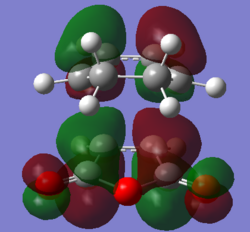
Energy / a.u.	-0.34271	-0.04048
Symmetry	Antisymmetric	Antisymmetric

Molecular Orbitals of Endo transition state

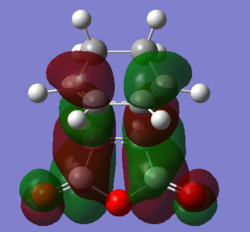
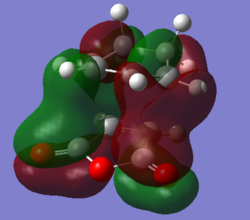
	HOMO	LUMO	HOMO - 12(Orbital 22)
Molecular Orbital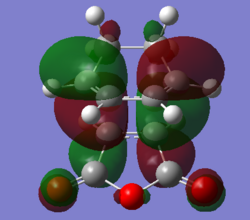
Energy / a.u.	-0.34506	0.03570	-0.54617
Symmetry	Antisymmetric	Antisymmetric	Antisymmetric

The MO diagrams confirm secondary orbital overlap is possible in the endo TS but not in the exo TS. The secondary orbital overlap in the endo TS can be observed in HOMO - 12(Orbital 22), the phase of the -(C=O)-O-(C=O)- fragment of maleic anhydride corresponds to that of the diene resulting in overlap between the in-phase p orbitals leading to overall stabilisation of the endo TS. Therefore the endo isomer is favoured despite having higher steric repulsion.

The results obtained is in agreement with literature, the endo product is favoured in a Diels Alder reaction due to its more stabilised transition. Therefore the endo is the kinetic product while exo is thermodynamic product.

Conclusion

Computational methods using Gaussian calculations was found to be useful in calculating and predicting transition states for kinetically controlled pericyclic reactions such as cycloaddition (Diels-Alder) or sigmatropic Cope rearrangement. Both steric and electronic aspects can be investigated by cacluating the energies, geometries, structures, frontier orbitals, and reaction coordinate/reaction pathways. This is helpful in predicting reactivity and selectivity of reactions.

An limitation of Gaussian calculations is that it can not predict if the reaction proceeds under kinetic or thermodynamic control so the major product of the reaction can not be determined. Larger(more complex) basis sets could have being investigated which will improve the calculations but will also use more time and resources, the DFT/B3LYP/6-31G(d) is a good compromise between accuracy and time. In addition, light controlled Diels-Alder reactions could be investigated.

Computational methods is a very powerful tool in pharmaceuticals, where it is used to model the binding of substrates to enzymes.