Rep:Mod:inorgcompquintinlo00690346

Inorganic Computational Experiment (Module 2) Quintin Lo CID: 00690346

Introduction

Computational chemistry is a branch of chemistry that uses computer simulations to solve complex problems in chemistry. It allows us to discern correlations between the properties and the structure of compounds and to simulate chemical reactions without having to carry out the experiment in the laboratory. One of the drawbacks to computational chemistry is that it is accurate only when small compounds are analysed and the accuracy also depends on the method used, which we will explore further in this experiment. There are numerous methods available, ranging from ab-initio methods to empirical and semi-empirical methods.

Part 1: Basic computational techniques

Optimisation of BH₃

3-21G Optimisation

The optimisation of BH₃ was done using Gaussview 5.0 with 3-21G basis-set. The 3-21G basis set is also known as a split valance basis set, where only the double zeta for the valance orbital is calculated as the inner shell electrons are not as important to the calculations. The log file for this optimisation can be found here File:Qlobh3optimisation.log.

Diagram 1: 3-21G optimised BH₃ molecule.

**BH₃ optimisation (Table 1)**
File Name	QLOBH3OPTIMISATION
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.46 au
RMS GRADIENT NORM	0.0000851 au
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	C_S

The gradient is close to zero (0.0000851 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000709     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672478D-07
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1947         -DE/DX =   -0.0002              !
 ! R2    R(1,3)                  1.1948         -DE/DX =   -0.0002              !
 ! R3    R(1,4)                  1.1944         -DE/DX =   -0.0001              !
 ! A1    A(2,1,3)              120.0157         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              119.9983         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.986          -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

**3-21G optimised BH₃ molecule (Table 2)**
Bond	Bond Length (Å)	Bond	Bond Angle (^o)
B1-H2	1.19	H4-B1-H3	120.0
B1-H4	1.19	H4-B1-H2	120.0
B1-H3	1.19	H2-B1-H3	120.0

The corresponding boron and hydrogen atoms are shown in diagram 1 above. The calculated B-H bond length in table 2 above corresponds to the experimentally determined bond length by Kawaguchi^[1], which was 1.19 Å. The three B-H bonds in the optimised BH₃ molecule was found to have slightly different bond lengths, but the deviations from the experimental bond lengths are extremely small (i.e. approximately ±0.006 Å) and these computational simulations are accurate to 0.01 Å, hence they are insignificant. Slight variations in bond angles were also observed, but in general the values are in good agreement with literature values^[2]. The discrepancies could be attributed to the 3-21G basis-set, which has extremely low accuracy.

The point group of this molecule is C_S and not D_3h due to previous adjustments to the bond lengths prior to optimisation.

6-31G(d,p) optimisation

The BH₃ molecule was further optimised using the 6-31G(d,p) basis set. The 6-31G(d,p) basis set is known as a higher level basis-set when compared to 3-21G. The 6-31G(d,p) is a polarised basis-set, where polarised functions are taken into account. These functions give the basis-set some flexibility so as to allow the orbitals to be unsymmetrical about the nucleus, which gives a more precise representation of the bonding between the boron and hydrogen atoms. The log file for this optimisation is shown here File:Qlobh3optimisationdp.log.

Diagram 2: 6-31G (d,p) optimised BH₃ molecule.

**BH₃ optimisation (Table 3)**
File Name	QLOBH3OPTIMISATIONDP
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.62 au
RMS GRADIENT NORM	0.00000707 au
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	C_S

The gradient is close to zero (0.00000707 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000061     0.001800     YES
 RMS     Displacement     0.000038     0.001200     YES
 Predicted change in Energy=-1.069855D-09
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1923         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.1923         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.1923         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0055         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0007         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.9939         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

**6-31G (d,p) optimised BH₃ molecule (Table 4)**
Bond	Bond Length (Å)	Bond	Bond Angle (^o)
B1-H2	1.19	H4-B1-H3	120.0
B1-H4	1.19	H4-B1-H2	120.0
B1-H3	1.19	H2-B1-H3	120.0

The corresponding boron and hydrogen atoms are shown in diagram 2 above. The B-H bond lengths show good correlation with the reported experimental values^[1] at 1.19 Å. The same could be said for the bond angles^[2]. It was observed that while 6-31G(d,p) optimisation took slightly longer when compared to 3-21G optimisation. This optimised BH₃ molecule is even closer to D_3h symmetry when compared to the 3-21G optimised BH₃ molecule.

The energy of the 3-21G optimised BH₃ molecule is -26.46 au while the energy of the 6-31G(d,p) optimised BH3 molecule is -26.62 au. Any comparisons made between these two energies are likely to be invalid as the basis set used to calculate these energies were different, one being 3-21G and the other 6-31G(d,p), where the calculated energy is highly dependent on the nature of the basis set.

The difference in energy is 0.16 au, which is equivalent to 420 kJ mol^-1.

Pseudo-potentials and basis-sets

Using pseudo-potentials and larger basis-sets

GaBr₃ was created using Gaussview 5.0. When compared to BH₃, GaBr₃ contains heavy atoms and hence pseudopotentials and a medium level basis set was used. The molecule was optimised using the LandL2DZ basis set option on a high performance computer (HPC). The results were published on D-Space^[3].

Diagram 3: LanL2DZ optimised GaBr₃ molecule.

**GaBr₃ optimisation using HPC (Table 5)**
File Name	Gabr3HPC
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.70 au
RMS GRADIENT NORM	0.00000016 au
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	D_3h

The gradient is close to zero (0.00000016 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282695D-12
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.3502         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.3502         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.3502         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

**LandL2DZ optimised GaBr₃ molecule (Table 6)**
Bond	Bond Length (Å)	Bond	Bond Angle (^o)
Ga1-Br2	2.35	Br4-Ga1-Br3	120.0
Ga1-Br4	2.35	Br4-Ga1-Br2	120.0
Ga1-Br3	2.35	Br2-Ga1-Br3	120.0

The gallium and bromine atoms correspond to the atoms shown in diagram 3. The computed Ga-Br bond length (2.35 Å) in table 3 was compared to the experimental value reported by Silva et. al.^[4] (2.33 Å) and the value in CRC handbook^[5] (2.249 Å), which showed a good correlation between computed and experimental values. Therefore it is safe to say that the result obtained is reasonable as the difference between the computed and literature values are extremely small and negligible.

Using a mixture of basis-sets and pseudo-potentials

BBr₃ contains a light atom (B) and heavy atoms (Br), which has a need for a full basis-set for Boron and a pseudo-potential for the heavy Bromine. The molecule was created using Gaussview 5.0 and the optimisation (Gen) was done using the HPC. The results were published on D-Space^[6].

**BBr₃ optimisation using HPC (Table 7)**
File Name	BBr3HPC
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	Gen
Charge	0
Spin	Singlet
E(RB3LYP)	-64.44 au
RMS GRADIENT NORM	0.00000974 au
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	C_s

The gradient is close to zero (0.00000974 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000018     0.000450     YES
 RMS     Force            0.000010     0.000300     YES
 Maximum Displacement     0.000106     0.001800     YES
 RMS     Displacement     0.000061     0.001200     YES
 Predicted change in Energy=-2.171373D-09
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.934          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.934          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.9339         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.002          -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0006         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.9974         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

**Gen optimised BBr₃ molecule (Table 8)**
Bond	Bond Length (Å)	Bond	Bond Angle (^o)
B1-Br2	1.93	Br4-B1-Br3	120.0
B1-Br4	1.93	Br4-B1-Br2	120.0
B1-Br3	1.93	Br2-B1-Br3	120.0

The boron and bromine atoms correspond to the atoms shown in diagram 4. The computed B-Br bond length shown in table 8 above correlates well with the value reported in literature (1.90 Å), which was obtained using X-ray crystallography^[7]. The computed bond angles also matches well with the values reported in literature^[7] (120 ^o). Further analysis is done below.

Analysis

**Summary of bond distances (Table 9)**
Bond	Mean Bond Length (Å)
B-H (6-31G(d,p))	1.19
B-Br	1.93
Ga-Br	2.35

It can be seen in table 9 that by increasing the size of the ligands (from H to Br), there was an increase in bond length due to an increase in atomic radii of the ligands. This could also be seen when we look into the electronic structures of both H and Br. H has 1 electron while Br has 35 electrons, therefore for larger atoms such as Br, it must be held further away from the B centre so as to avoid repulsive interactions. This is also known as the van der waals radii. Since both BH₃ and BBr₃ have the same central B atom, the observed differences were entirely dependent on the nature of the ligand.

Both H and Br atoms are one electron away from having a full valance shell, where both atoms uses 1 electron to form a covalent bond. However, the similarities between the two atoms end there. It is important to take note that the electron H uses to form a bond comes from the 1s orbital while in the case of Br, it accepts an electron to a 4p orbital to form a stable valance 4p shell. This suggests that a B-H bond is stronger when compared to a B-Br bond, which was confirmed by Cottrell et.al.,^[8]^,^[9] where the reported B-H bond strength is 390 kJ mol^-1 and the reported B-Br bond strength is 380 kJ mol^-1.

The same trend could be seen when the central atom was changed from B to Ga, where the same ligands were used in both molecules. Ga is larger and hence it has a greater atomic radii than B, as Ga has 31 electrons compared to the 5 electrons in B. Therefore the ligands must be held further away from Ga as compared to B so as to avoid repulsive interactions between the two large atoms.

Both B and Ga are in group 13 of the periodic table, with Ga being further down the group. Both atoms use 3 electrons to form covalent bonds. Boron is electron deficient and hence it is a stronger Lewis acid as compared to Ga. B containing compounds readily undergoes dimerisation due to its electron deficient nature while Ga containing compounds do not form dimers as it is less lewis acidic. The difference in Lewis acidity indicates that Ga is likely to form weaker bonds with Lewis bases as compared to B.

A chemical bond is the underlying basis of chemistry, which explains a wide variety of concepts in chemistry. It is an attraction between two atoms, possibly due to electrostatic interactions between the nuclei and the electrons of both atoms. It is this attraction that leads to the formation of molecules and compounds, without a chemical bond, we won't be able to explain a lot things we see in chemistry. There are several types of chemical bonds such as ionic, covalent and hydrogen bonds just to name a few.

It is important to note that in reality, a chemical bond is not just a straight line as shown in Gaussview, the only reason it is drawn as a straight line is for simplification purposes. Gaussview does optimisations based on a given set of parameters which are defined by the user, when the result of such optimisations fall outside of these parameters, the "bond" will disappear. This is not to say that a bond does not exist in reality, it just tells us that based on the parameters defined by the user, the bond does not "exist".

Further analysis of BH₃ and GaBr₃

Frequency analysis of BH₃

Frequency analysis is essentially the second derivative of the potential energy surface, which allows us to differentiate between a minimum and a transition state on the potential energy surface. If the frequencies are all positive then a minimum is present and if negative frequencies are present, we have a transition state. As we will see later, the frequency analysis allows us to generate an IR spectrum of the molecule, illustrating the different vibrational modes of the molecule.

The frequency analysis was done on the 6-31G(d,p) optimised BH₃ molecule using Gaussview 5.0. The molecule was restricted to a D_3h symmetry. The log file for this calculation is shown here. File:Qlobh3frequency2.log

**Frequency analysis of BH₃ (Table 10)**
File Name	QLOBH3FREQUENCY2
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-25.62 au
RMS GRADIENT NORM	0.00000291 au
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	D_3h

The gradient is close to zero (0.00000291 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000023     0.001800     YES
 RMS     Displacement     0.000015     0.001200     YES
 Predicted change in Energy=-2.008834D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.1923         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.1923         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.1923         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Low frequencies ---   0   0   0   6   12   12
 Low frequencies --- 1162.9963 1213.1826 1213.1853

A minimum is present as there are no negative frequencies. It is also important to note that BH₃ is a non-linear molecule, which tells us that there are 3N-6 vibrational degrees of freedom, where the low frequencies in the first line represent the value of "6" in 3N-6.

The energy of the molecule reported in table 9 is the same as the energy reported earlier for the 6-31G(d,p) optimised molecule. This confirms that there were no changes in the structure during the frequency analysis. The six frequencies are within the acceptable range of ±15 cm^-1.

Animating the vibrations in BH₃

The vibration animations were done on Gaussview 5.0 and the different forms of motion are described in table 11 below. This also allows us to generate the computed IR spectrum shown in diagram 5.

**Vibrational analysis of BH₃ (Table 11)**
Mode	Form of vibration	Frequency (cm^-1)	Intensity	Symmetry D_3h point group
1	The H atoms moves in and out of the plane while the B atom remains stationary.	1163	93	A₂'
2	The B atom and one of the H atoms move slightly upwards and downwards while the other two H atoms move in and out together in a concerted motion.	1213	14	E'
3	The H atoms on the left and right move in and out but in opposite directions while the remaining H atom and the B atom moves from left to right in a concerted fashion.	1213	14	E'
4	The B atom is stationary while all three H atoms move in and out in a concerted manner.	2582	0	totally symmetric, A₁'
5	One of the H atoms remains stationary while the other two H atoms moves in and out and the B atom moves from left to right in a concerted manner.	2715	126	E'
6	The B atom moves very little while one of the H atoms move upwards and downwards and the other two H atoms move in and out together in a concerted motion.	2715	126	E'

BH₃ has 6 different modes of vibrations, each with a definite frequency. Even though the vibrational modes are distinct in terms of the way the atoms move, some of the them are degenerate as they have the same frequency. Therefore the number of IR peaks is less than the number of modes of vibrations. The vibrational mode at 2582 cm^-1 has an intensity of 0, which means it does not appear on the spectrum. Thus we can conclude that this vibrational mode is not IR active where the source of inactivity is due to its completely symmetrical vibrational mode, which prevents it from absorbing IR light.

Frequency Analysis of GaBr₃

Further analysis was done on the LandL2DZ GaBr₃ molecule. In order to ensure that the molecule is at a minimum, it was subjected to frequency analysis using Gaussview 5.0 and the results are shown below. The log file for this analysis can be found here File:QLOGABR3FREQUENCY.LOG.

**Frequency analysis of GaBr₃ (Table 12)**
File Name	QLOGABR3frequency
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LandL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.70 a.u.
RMS GRADIENT NORM	0.00000011 a.u.
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	D_3h

The gradient is close to zero (0.00000011 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282694D-12
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.3502         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.3502         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.3502         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Low frequencies ---   0   0   0  0    0    1
 Low frequencies ---   76.3744   76.3753   99.6982

The frequency analysis was carried out correctly as there was no observable change in the energy of the molecule. A minimum was obtained as there are no negative frequencies. As with BH₃, GaBr₃ is a non-linear molecule, hence it has 3N-6 vibrational degrees of freedom, where the value of "6" is shown above.

**Vibrational analysis of GaBr₃ (Table 13)**
Mode	Form of vibration	Frequency (cm^-1)	Intensity	Symmetry D_3h point group
1	The central Ga atom moves from left to right together with one of the Br atoms. The other two Br atoms move up and down in opposite directions in a concerted manner.	76	3	E'
2	The central Ga atom together with one of the Br atoms moves up and down in concerted motion while the other two Br atoms move in and out in a coordinated manner.	76	3	E'
3	All four atoms move in and out of the plane but in opposite directions.	99	9	A₂'
4	The Ga atom remains stationary while all three Br atoms move in and out in a concerted fashion.	197	0	totally symmetric, A₁'
5	One of the Br atoms remains stationary while the two of the Br atoms move in and out in opposite directions and the remaining Ga atom moves from left to right in a concerted manner.	316	57	E'
6	The two Br atoms on the side moves very little while the remaining Br atom together with the Ga atom moves up and down in opposite directions in a concerted manner.	316	57	E'

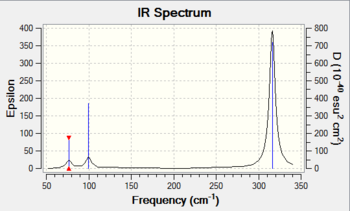
GaBr₃ has 6 vibrational modes but it only has 3 peaks in the IR spectrum (diagram 6). This is due to degenerate vibrational modes, where some vibrational modes have the same frequency even though each mode is distinct in terms of the motion of individual atoms associated with the molecule. The IR inactive peak is at 197 cm-1, which has an intensity of 0. As mentioned earlier, this is due to the totally symmetrical mode of vibration at this frequency.

Comparison between BH₃ and GaBr₃

**Frequencies of BH₃ and GaBr₃ (Table 14)**
Mode (BH₃)	Frequency (cm^-1)	Mode (GaBr₃)	Frequency (cm^-1)
1	1163	1	76
2	1213	2	76
3	1213	3	99
4	2582	4	197
5	2715	5	316
6	2715	6	316

The obvious difference in the frequencies of BH₃ and GaBr₃ is the fact that the frequencies for GaBr₃ is lower than that of BH₃. As mentioned earlier, Ga-Br bonds (2.35 Å) are longer than B-H bonds (1.19 Å) and as a result, Ga-Br bonds are known to be weaker than their B-H counterparts, which leads to lower frequencies in the IR spectrum of GaBr₃ as compared to the BH₃. An alternative explanation for the differences in frequency was put forward by Atkins and de Paula^[10], where the formula for the frequency (v) of absorption band was given by the equation 1 below:

where k is the spring constant for the B-H or Ga-Br bond, c is the speed of light and μ is the reduced mass of the B-H or Ga-Br bond. The reduced mass μ is given by equation 2 below:

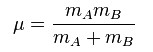
where m_A is the mass of atom A and m_B is mass of atom B.

It is clear that the reduced mass of the Ga-Br bond is greater than that of the B-H bond. Since the reduced mass is inversely proportional to the frequency of absorbance, the frequencies for GaBr₃ will definitely be lower than that of BH₃. This theory is further reinforced by the fact that the force constant of the Ga-Br bond is lower than that of the B-H bond, where the force constant is directly proportional to the frequency of absorbance as shown in equation 1.

There has been a reordering of modes. In BH₃, the first vibrational mode started off 1163 cm^-1 with a symmetry of A₂' followed by two E' vibrational modes as shown in table 11, while in GaBr₃, the first vibrational mode was at 76 cm^-1 with a E' symmetry followed by another E' and an A₂' vibrational modes as shown in table 13.

The IR spectra of BH₃ and GaBr₃ both contain 3 peaks where both molecules contains degenerate vibrational modes. Another similarity between these two molecules is the fact that both contain one IR inactive vibrational mode, which is rationalised by the symmetric A₁' vibrational mode.

The A₂' vibrational modes lie close to the E' vibrational modes while the A₁' vibrational modes lie close to the E' modes but are higher in energy. They are higher in energy because A₁' and E' vibrational modes in both BH₃ and GaBr₃ involve a greater displacement of all four atoms from their equilibrium positions as compared to the A₂' and E' vibrational modes. These stretching and bending motions require a considerable amount of energy as we need to overcome the attractive interactions between two atoms in a bond without breaking the bond. Hence the larger the displacement of atoms from their equilibrium positions, the higher the energy of the vibrational mode.

The same method and basis set for both optimisation and frequency analysis was used for calculations so that meaningful comparisons can be made between the results obtained in this experiment as the energy of the molecule is highly dependent on the method and basis set used. During optimisation and frequency analysis, the method and basis set determines the parameters used to solve the Schrodinger equation for the nuclear positions and electrons which in turn will allow us to obtain the energy of the molecule. Hence using different methods and basis sets will give different energies for the same molecule which will invalidate any comparisons that were made.

Frequency analysis gives the second derivative of the potential energy surface, which allows us to differentiate between a minimum on the potential energy surface or a transition state. Positive frequencies indicate the presence of a minimum while negative frequencies indicates a transition state is present instead of a minimum. This also allows us to generate a computed IR spectrum of a molecule and visualise the vibrational modes of a molecule as shown earlier.

It must be noted that a tight optimisation was used to obtain frequencies close to zero. 'Low frequencies' represents the frequency for rotation and translational motion of the molecule under investigation.^[11]

Molecular orbitals of BH₃

The molecular orbitals of the 6-31G(d,p) optimised BH₃ was analysed using Gaussview. The table below shows the first eight molecular orbitals (MO) of BH₃. The checkpoint file used can be found here. File:Qlobh3optimisationday3.chk

**MOs of BH₃ (Table 15)**
Number	Energy (au)	Number	Energy (au)
1	-6.77	5	-0.06
2	-0.51	6	0.16
3	-0.35	7	0.18
4	-0.35	8	0.18

Diagram 7: MO diagram of trigonal planar BH₃, showing both "real" MOs and "LCAO" MOs.

As shown in diagram 7 above, there are no significant differences between the real and LCAO MOs. This tells us that qualitative MO theory is very useful in allowing us to predict the real MOs of BH₃ without using a computer. However, BH₃ is a rather simple molecule, which might be a reason why the real and LCAO MOs look very similar. Further investigations must be made for more complex molecules before we can determine whether qualitative MO theory is indeed useful and accurate.

Analysis of NH₃

Optimisation and frequency analysis of NH₃

NH₃ was optimised on Gaussview 5.0 using the 6-31G(d,p) basis set, the frequency of NH3 was analysed at the same time using the Opt+Freq option in the Gaussian calculation setup window. Frequency analysis allows us to check if a minimum is present. The file for this analysis can be found here.File:QLONH3OPTFREQ1.LOG

**Optimisation and Frequency analysis of NH₃ (Table 16)**
File Name	qlonh3optfreq1
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.56 au
RMS GRADIENT NORM	0.00000323 au
Imaginary Freq	0
Dipole Moment	1.85 Debye
Point Group	C_3V

The gradient is close to zero (0.00000885 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000015     YES
 RMS     Force            0.000004     0.000010     YES
 Maximum Displacement     0.000014     0.000060     YES
 RMS     Displacement     0.000009     0.000040     YES
 Predicted change in Energy=-1.141602D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.018          -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.018          -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.018          -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              105.7446         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              105.7446         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              105.7446         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)           -111.8637         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Low frequencies ---   0   0   0    7    8   8
 Low frequencies --- 1089.3834 1693.9368 1693.9368

The frequency analysis did not result in a change the energy of the NH₃ molecule, hence it was carried out correctly. A minimum was obtained as there are no negative frequencies. As mentioned before, NH₃ is a non-linear molecule and hence it has 3N-6 vibrational degrees of freedom, where the value of "6" is shown in above (low frequencies).

The vibrations were then animated using Gaussview and are shown in the table below.

**Vibrational analysis of NH₃ (Table 17)**
Mode	Form of vibration	Frequency	Intensity	Symmetry C_3V point group
1	All three H atoms are moving in and out of the plane with little movement from N.	1089	145	A₁
2	All three H atoms are moving in different directions in a concerted motion while there is little movement from N.	1640	14	E
3	Two H atoms are moving up and down while the other H atom moves in and out of the plane. Slight movement from N.	1640	141	E
4	All three H atoms are moving in and out in a concerted manner, while N moves slightly.	3461	1	totally symmetric, A₁
5	One H atom is stationary while the other two H atoms are moving in and out in concerted motion with little movement from N.	3590	0	E
6	All three H atoms are moving in and out with one H atom moving in an opposite direction with respect to the other two H atoms. There is slight movement from N.	3590	0	E

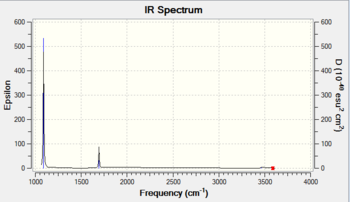
There are only 2 observable peaks in the IR spectrum of NH₃ even though there are 6 vibrational modes. This is due to the degeneracy of the vibrational modes where the vibrational modes are distinct in terms of the motion of atoms but are the same in terms of their frequencies. The A₁ vibrational mode has a rather low intensity (1), hence it could not be seen in the spectrum. The low intensity is probably due to the symmetric nature of the vibrational mode.

MOs of NH₃

**MOs of NH₃ (Table 18)**
Number	Energy	Number	Energy
1	-14.3568	5	-0.25318
2	-0.84466	6	0.07985
3	-0.45030	7	0.16923
4	-0.45030	8	0.16923

As with the case of BH₃, there were no significant differences between the real and LCAO MOs in NH₃. This shows that qualitative MO theory is accurate in this case and is useful in determining the MOs of NH₃.

Natural Bond Orbital (NBO) Analysis of NH₃

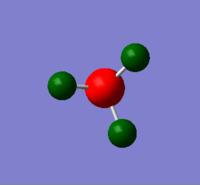
NBO analysis was done using Gaussview 5.0 and the results are shown in diagram 9. The file for this analysis is shown here. File:QLONH3FREQUENCY11.LOG

As shown in the diagram, the nitrogen atom is bright red, which indicates the presence of a large negative charge. This was expected due to the electronegativity of nitrogen. The bright green colour on the hydrogen atoms shows the presence of a high positive charge, which again is due to the polar N-H bond in NH₃. The charge range in this case is between -1.000 and +1.000.

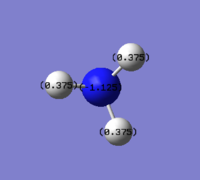
Diagram 10: NBO analysis of NH₃ showing specific NBO charges

The NBO charges as shown in the diagram 10 above illustrates the specific NBO charges for nitrogen and hydrogen atoms which are -1.125 and 0.375 respectively. It was noted that the nitrogen atom is outside of the -1.000 to +1.000 charge range.

Association energies: Ammonia-Borane

Ammonia-Borane was optimised using Gaussview 5.0 at the B3LYP/6-31G(d,p) level. Additional keywords such as 'int=ultrafine' and 'SCF=conver=9' were used to ensure a better optimisation takes place. The log file for this optimisation can be found here. File:QLOBH3NH3OPTIMISATIONSCF.LOG.

**Optimisation of NH₃BH₃ (Table 19)**
File Name	QLOBH3NH3OPTIMISATIONSCF
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.22 au
RMS GRADIENT NORM	0.00000047 au
Imaginary Freq	0
Dipole Moment	5.56 Debye
Point Group	C_3V

The gradient is very small and is close to zero (0.00000047 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000008     0.000060     YES
 RMS     Displacement     0.000004     0.000040     YES
 Predicted change in Energy=-1.705809D-11
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  1.2098         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  1.2098         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  1.2098         -DE/DX =    0.0                 !
 ! R4    R(1,5)                  1.6677         -DE/DX =    0.0                 !
 ! R5    R(5,6)                  1.0185         -DE/DX =    0.0                 !
 ! R6    R(5,7)                  1.0185         -DE/DX =    0.0                 !
 ! R7    R(5,8)                  1.0185         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              113.8737         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              113.8737         -DE/DX =    0.0                 !
 ! A3    A(2,1,5)              104.5976         -DE/DX =    0.0                 !
 ! A4    A(3,1,4)              113.8737         -DE/DX =    0.0                 !
 ! A5    A(3,1,5)              104.5976         -DE/DX =    0.0                 !
 ! A6    A(4,1,5)              104.5976         -DE/DX =    0.0                 !
 ! A7    A(1,5,6)              111.023          -DE/DX =    0.0                 !
 ! A8    A(1,5,7)              111.023          -DE/DX =    0.0                 !
 ! A9    A(1,5,8)              111.023          -DE/DX =    0.0                 !
 ! A10   A(6,5,7)              107.8759         -DE/DX =    0.0                 !
 ! A11   A(6,5,8)              107.8759         -DE/DX =    0.0                 !
 ! A12   A(7,5,8)              107.8759         -DE/DX =    0.0                 !
 ! D1    D(2,1,5,6)             60.0            -DE/DX =    0.0                 !
 ! D2    D(2,1,5,7)            180.0            -DE/DX =    0.0                 !
 ! D3    D(2,1,5,8)            -60.0            -DE/DX =    0.0                 !
 ! D4    D(3,1,5,6)            180.0            -DE/DX =    0.0                 !
 ! D5    D(3,1,5,7)            -60.0            -DE/DX =    0.0                 !
 ! D6    D(3,1,5,8)             60.0            -DE/DX =    0.0                 !
 ! D7    D(4,1,5,6)            -60.0            -DE/DX =    0.0                 !
 ! D8    D(4,1,5,7)             60.0            -DE/DX =    0.0                 !
 ! D9    D(4,1,5,8)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Once the molecule was confirmed to be optimised, a frequency analysis of NH₃BH₃ was carried out. The file for the frequency analysis can be found here. File:QLOBH3NH3FREQSCF.LOG

**Frequency analysis of NH₃BH₃ (Table 20)**
File Name	QLOBH3NH3FREQSCF
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.22 a.u.
RMS GRADIENT NORM	0.00000052 a.u.
Imaginary Freq	0
Dipole Moment	5.56 Debye
Point Group	C_3V

Low frequencies ---   0   0   0    0    0   0
 Low frequencies ---  263.3086  632.9964  638.4686

There are no negative frequencies, hence a minimum is present.

Association energy calculation for NH₃BH₃

The reaction between NH₃ and BH₃ is shown in the following equation:

NH₃ + BH₃ -> NH₃BH₃

The energies of each molecule in this reaction are shown below:

E(NH₃)= -56.55 au

E(BH₃)= -26.62 au

E(NH₃BH₃)= -83.22 au

The energy difference is given by ΔE = E(NH₃BH₃)-[E(NH₃)+E(BH₃)], where ΔE is equal to -0.05 au which is equivalent to -140 kJ mol^-1.

Therefore we can conclude that the association energy and the dissociation energy of NH₃BH₃ are -140 kJ mol^-1 and 140 kJ mol^-1 respectively.

The dissociation energy of NH₃BH₃ was then compared to the experimental value reported by Haaland^[12] (31 kcal mol^-1, which is equivalent to 130 kJ mol^-1), which showed relatively good correlation between experimental and computed values.

Part 2 (mini project): Lewis acids and bases

The conformers, vibrations and MOs of Al₂Cl₄Br₂ are investigated in this section using Gaussview 5.0. The 6-31G(d,p) basis set was used for Al and Cl and a pseudo-potential LanL2DZ was used for the heavy atom Br.

Monomers

Optimisation of AlCl₃

AlCl₃ was first optimised using Gaussview 5.0 using the 6-31G(d,p) basis set. A tight convergence criteria was set to ensure the optimisation is good. The file for this optimisation can be found below. File:QLOALCL3OPTIMISATION.LOG

Diagram 11: AlCl₃ with the atoms labelled.

**Optimisation of AlCl₃ (Table 21)**
File Name	qloalcl3optmisation
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-1623.23 au
RMS GRADIENT NORM	0.00000007 au
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	D_3h

The gradient is close to zero (0.00000007 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000001     0.000060     YES
 RMS     Displacement     0.000001     0.000040     YES
 Predicted change in Energy=-1.670988D-13
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.0874         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.0874         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.0874         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.0            -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.0            -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              120.0            -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

**6-31G(d,p) optimised AlCl₃ molecule (Table 22)**
Bond	Bond Length (Å)	Bond	Bond Angle (^o)
Al1-Cl2	2.09	Cl4-Al1-Cl3	120.0
A1-Cl3	2.09	Cl4-Al1-Cl2	120.0
Al1-Cl4	2.09	Cl2-Al1-Cl3	120.0

The computed bond length (2.09 Å) is close to the reported bond length in literature^[5] (2.063 Å), a difference of 0.027 Å is small and negligible. The computed bond angles are consistent and hence the optimisation of AlCl₃ was carried out correctly.

Optimisation of AlCl₂Br

AlCl₂Br was then optimised using the LanL2DZ basis set as it contains a heavy Br atom, which means the 6-31G(d,p) basis set cannot be used. A tight convergence criteria was set to ensure good optimisation. The log file for this optimisation can be found here. File:QLOALCL2BROPTIMISATION.LOG

Diagram 12: AlCl₂Br with the atoms labelled.

**Optimisation of AlCl₂Br (Table 23)**
File Name	qloalcl2broptmisation
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-45.22 au
RMS GRADIENT NORM	0.00000031 au
Imaginary Freq	0
Dipole Moment	0.52 Debye
Point Group	C_2V

The gradient is close to zero (0.00000031 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000007     0.000060     YES
 RMS     Displacement     0.000004     0.000040     YES
 Predicted change in Energy=-4.705638D-12
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,2)                  2.3355         -DE/DX =    0.0                 !
 ! R2    R(1,3)                  2.1782         -DE/DX =    0.0                 !
 ! R3    R(1,4)                  2.1782         -DE/DX =    0.0                 !
 ! A1    A(2,1,3)              120.3531         -DE/DX =    0.0                 !
 ! A2    A(2,1,4)              120.3531         -DE/DX =    0.0                 !
 ! A3    A(3,1,4)              119.2938         -DE/DX =    0.0                 !
 ! D1    D(2,1,4,3)            180.0            -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

**LanL2DZ optimised AlCl₂Br molecule (Table 24)**
Bond	Bond Length (Å)	Bond	Bond Angle (^o)
Al1-Br2	2.34	Cl4-Al1-Cl3	119.2
A1-Cl3	2.18	Cl4-Al1-Br2	120.4
Al1-Cl4	2.18	Br2-Al1-Cl3	120.4

No literature value was found for the bond lengths and angles for the AlCl₂Br molecule.

Isomers of Al₂Cl₄Br₂

There are four different isomers of Al₂Cl₄Br₂ and they are shown in diagram 13 below.

Optimisation

Optimisation of isomer 1

Isomer 1 was optimised using the LanL2DZ basis set with a tight convergence criteria on Gaussview 5.0, where the keywords "int=ultrafine" were used. The results are shown in table 25 below. The log file for this calculation is shown here. File:QLOAL2CL4BR2OPTIMISATION2.LOG

**Optimisation of Isomer 1 (Table 25)**
File Name	qloal2cl4br2optimisation2
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.46 au
RMS GRADIENT NORM	0.000000197 au
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	D_2h

The gradient is very small and is close to zero (0.000000197 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000003     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000028     0.000060     YES
 RMS     Displacement     0.000012     0.000040     YES
 Predicted change in Energy=-2.131688D-10
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,5)                  2.1805         -DE/DX =    0.0                 !
 ! R2    R(1,6)                  2.1805         -DE/DX =    0.0                 !
 ! R3    R(1,7)                  2.5878         -DE/DX =    0.0                 !
 ! R4    R(1,8)                  2.5878         -DE/DX =    0.0                 !
 ! R5    R(2,3)                  2.1805         -DE/DX =    0.0                 !
 ! R6    R(2,4)                  2.1805         -DE/DX =    0.0                 !
 ! R7    R(2,7)                  2.5878         -DE/DX =    0.0                 !
 ! R8    R(2,8)                  2.5878         -DE/DX =    0.0                 !
 ! A1    A(5,1,6)              122.9186         -DE/DX =    0.0                 !
 ! A2    A(5,1,7)              109.9006         -DE/DX =    0.0                 !
 ! A3    A(5,1,8)              109.9006         -DE/DX =    0.0                 !
 ! A4    A(6,1,7)              109.9013         -DE/DX =    0.0                 !
 ! A5    A(6,1,8)              109.9013         -DE/DX =    0.0                 !
 ! A6    A(7,1,8)               89.1314         -DE/DX =    0.0                 !
 ! A7    A(3,2,4)              122.9186         -DE/DX =    0.0                 !
 ! A8    A(3,2,7)              109.9006         -DE/DX =    0.0                 !
 ! A9    A(3,2,8)              109.9006         -DE/DX =    0.0                 !
 ! A10   A(4,2,7)              109.9013         -DE/DX =    0.0                 !
 ! A11   A(4,2,8)              109.9013         -DE/DX =    0.0                 !
 ! A12   A(7,2,8)               89.1314         -DE/DX =    0.0                 !
 ! A13   A(1,7,2)               90.8687         -DE/DX =    0.0                 !
 ! A14   A(1,8,2)               90.8686         -DE/DX =    0.0                 !
 ! D1    D(5,1,7,2)           -110.882          -DE/DX =    0.0                 !
 ! D2    D(6,1,7,2)            110.8969         -DE/DX =    0.0                 !
 ! D3    D(8,1,7,2)              0.0071         -DE/DX =    0.0                 !
 ! D4    D(5,1,8,2)            110.882          -DE/DX =    0.0                 !
 ! D5    D(6,1,8,2)           -110.897          -DE/DX =    0.0                 !
 ! D6    D(7,1,8,2)             -0.0071         -DE/DX =    0.0                 !
 ! D7    D(3,2,7,1)            110.882          -DE/DX =    0.0                 !
 ! D8    D(4,2,7,1)           -110.897          -DE/DX =    0.0                 !
 ! D9    D(8,2,7,1)             -0.0071         -DE/DX =    0.0                 !
 ! D10   D(3,2,8,1)           -110.882          -DE/DX =    0.0                 !
 ! D11   D(4,2,8,1)            110.8969         -DE/DX =    0.0                 !
 ! D12   D(7,2,8,1)              0.0071         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Optimisation of isomer 2

Isomer 2 was then optimised under the same conditions using the LanL2DZ basis set, where a tight convergence criteria was used together with the keywords "int=ultrafine". The log file for this optimisation can be found here. File:QLOISOMER2OPTIMISATION.LOG

**Optimisation of Isomer 2 (Table 26)**
File Name	qloisomer2optmisation
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.47 au
RMS GRADIENT NORM	0.000000095 au
Imaginary Freq	0
Dipole Moment	0.84 Debye
Point Group	C₁

The gradient is close to zero (0.000000095 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000034     0.000060     YES
 RMS     Displacement     0.000009     0.000040     YES
 Predicted change in Energy=-1.954841D-11
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,3)                  2.5825         -DE/DX =    0.0                 !
 ! R2    R(1,4)                  2.4113         -DE/DX =    0.0                 !
 ! R3    R(1,6)                  2.1783         -DE/DX =    0.0                 !
 ! R4    R(1,7)                  2.1789         -DE/DX =    0.0                 !
 ! R5    R(2,3)                  2.5996         -DE/DX =    0.0                 !
 ! R6    R(2,4)                  2.4251         -DE/DX =    0.0                 !
 ! R7    R(2,5)                  2.1818         -DE/DX =    0.0                 !
 ! R8    R(2,8)                  2.337          -DE/DX =    0.0                 !
 ! A1    A(3,1,4)               87.5617         -DE/DX =    0.0                 !
 ! A2    A(3,1,6)              110.4442         -DE/DX =    0.0                 !
 ! A3    A(3,1,7)              110.2081         -DE/DX =    0.0                 !
 ! A4    A(4,1,6)              110.0483         -DE/DX =    0.0                 !
 ! A5    A(4,1,7)              109.8039         -DE/DX =    0.0                 !
 ! A6    A(6,1,7)              123.0724         -DE/DX =    0.0                 !
 ! A7    A(3,2,4)               86.8844         -DE/DX =    0.0                 !
 ! A8    A(3,2,5)              109.4287         -DE/DX =    0.0                 !
 ! A9    A(3,2,8)              111.0149         -DE/DX =    0.0                 !
 ! A10   A(4,2,5)              109.1805         -DE/DX =    0.0                 !
 ! A11   A(4,2,8)              110.3894         -DE/DX =    0.0                 !
 ! A12   A(5,2,8)              123.7757         -DE/DX =    0.0                 !
 ! A13   A(1,3,2)               88.6256         -DE/DX =    0.0                 !
 ! A14   A(1,4,2)               96.9225         -DE/DX =    0.0                 !
 ! D1    D(4,1,3,2)             -0.5604         -DE/DX =    0.0                 !
 ! D2    D(6,1,3,2)            109.9461         -DE/DX =    0.0                 !
 ! D3    D(7,1,3,2)           -110.7836         -DE/DX =    0.0                 !
 ! D4    D(3,1,4,2)              0.6049         -DE/DX =    0.0                 !
 ! D5    D(6,1,4,2)           -110.2881         -DE/DX =    0.0                 !
 ! D6    D(7,1,4,2)            111.2234         -DE/DX =    0.0                 !
 ! D7    D(4,2,3,1)              0.5575         -DE/DX =    0.0                 !
 ! D8    D(5,2,3,1)           -108.6931         -DE/DX =    0.0                 !
 ! D9    D(8,2,3,1)            111.2201         -DE/DX =    0.0                 !
 ! D10   D(3,2,4,1)             -0.6013         -DE/DX =    0.0                 !
 ! D11   D(5,2,4,1)            108.8965         -DE/DX =    0.0                 !
 ! D12   D(8,2,4,1)           -111.8807         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Optimisation of isomer 3

Isomer 3 was optimised using the LanL2DZ basis set on Gaussview 5.0, where again a tight convergence criteria was used together with the keywords "int=ultrafine". The log file for this calculation can be found here. File:QLOISOMER31.LOG

**Optimisation of Isomer 3 (Table 27)**
File Name	isomer31
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.47 au
RMS GRADIENT NORM	0.000000084 au
Imaginary Freq	0
Dipole Moment	0.89 Debye
Point Group	C_2v

The gradient is close to zero (0.000000084 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000006     0.000060     YES
 RMS     Displacement     0.000002     0.000040     YES
 Predicted change in Energy=-5.876359D-12
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,3)                  2.4361         -DE/DX =    0.0                 !
 ! R2    R(1,4)                  2.4362         -DE/DX =    0.0                 !
 ! R3    R(1,5)                  2.3386         -DE/DX =    0.0                 !
 ! R4    R(1,6)                  2.3386         -DE/DX =    0.0                 !
 ! R5    R(2,3)                  2.407          -DE/DX =    0.0                 !
 ! R6    R(2,4)                  2.407          -DE/DX =    0.0                 !
 ! R7    R(2,7)                  2.1768         -DE/DX =    0.0                 !
 ! R8    R(2,8)                  2.1768         -DE/DX =    0.0                 !
 ! A1    A(3,1,4)               84.7937         -DE/DX =    0.0                 !
 ! A2    A(3,1,5)              109.9984         -DE/DX =    0.0                 !
 ! A3    A(3,1,6)              109.9985         -DE/DX =    0.0                 !
 ! A4    A(4,1,5)              109.9971         -DE/DX =    0.0                 !
 ! A5    A(4,1,6)              109.9972         -DE/DX =    0.0                 !
 ! A6    A(5,1,6)              124.8274         -DE/DX =    0.0                 !
 ! A7    A(3,2,4)               86.0688         -DE/DX =    0.0                 !
 ! A8    A(3,2,7)              110.3414         -DE/DX =    0.0                 !
 ! A9    A(3,2,8)              110.3416         -DE/DX =    0.0                 !
 ! A10   A(4,2,7)              110.3427         -DE/DX =    0.0                 !
 ! A11   A(4,2,8)              110.3429         -DE/DX =    0.0                 !
 ! A12   A(7,2,8)              123.2051         -DE/DX =    0.0                 !
 ! A13   A(1,3,2)               94.5688         -DE/DX =    0.0                 !
 ! A14   A(1,4,2)               94.5687         -DE/DX =    0.0                 !
 ! D1    D(4,1,3,2)              0.0009         -DE/DX =    0.0                 !
 ! D2    D(5,1,3,2)           -109.4052         -DE/DX =    0.0                 !
 ! D3    D(6,1,3,2)            109.4072         -DE/DX =    0.0                 !
 ! D4    D(3,1,4,2)             -0.0009         -DE/DX =    0.0                 !
 ! D5    D(5,1,4,2)            109.4065         -DE/DX =    0.0                 !
 ! D6    D(6,1,4,2)           -109.4085         -DE/DX =    0.0                 !
 ! D7    D(4,2,3,1)             -0.0009         -DE/DX =    0.0                 !
 ! D8    D(7,2,3,1)            110.2513         -DE/DX =    0.0                 !
 ! D9    D(8,2,3,1)           -110.2533         -DE/DX =    0.0                 !
 ! D10   D(3,2,4,1)              0.0009         -DE/DX =    0.0                 !
 ! D11   D(7,2,4,1)           -110.25           -DE/DX =    0.0                 !
 ! D12   D(8,2,4,1)            110.252          -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

Optimisation of isomer 4

Finally, isomer 4 was optimised using the LanL2DZ basis set where a tight convergence criteria was used together with the keywords "int=ultrafine". The log file can be found here. File:QLOISOMER4.LOG

**Optimisation of Isomer 4 (Table 27)**
File Name	qloisomer4
File Type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.47 au
RMS GRADIENT NORM	0.000000097 au
Imaginary Freq	0
Dipole Moment	0.96 Debye
Point Group	C_2v

The gradient is very small and is close to zero (0.000000097 au), which indicates that optimisation has occurred. This was further confirmed by the convergence of all forces in the table below.

Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000007     0.000060     YES
 RMS     Displacement     0.000004     0.000040     YES
 Predicted change in Energy=-3.082294D-12
 Optimization completed.
    -- Stationary point found.
                           ----------------------------
                           !   Optimized Parameters   !
                           ! (Angstroms and Degrees)  !
 --------------------------                            --------------------------
 ! Name  Definition              Value          Derivative Info.                !
 --------------------------------------------------------------------------------
 ! R1    R(1,3)                  2.4212         -DE/DX =    0.0                 !
 ! R2    R(1,4)                  2.4213         -DE/DX =    0.0                 !
 ! R3    R(2,3)                  2.4213         -DE/DX =    0.0                 !
 ! R4    R(2,4)                  2.4212         -DE/DX =    0.0                 !
 ! R5    R(3,5)                  2.3352         -DE/DX =    0.0                 !
 ! R6    R(3,8)                  2.1797         -DE/DX =    0.0                 !
 ! R7    R(4,6)                  2.3352         -DE/DX =    0.0                 !
 ! R8    R(4,7)                  2.1797         -DE/DX =    0.0                 !
 ! A1    A(3,1,4)               94.566          -DE/DX =    0.0                 !
 ! A2    A(3,2,4)               94.5659         -DE/DX =    0.0                 !
 ! A3    A(1,3,2)               85.4221         -DE/DX =    0.0                 !
 ! A4    A(1,3,5)              110.7247         -DE/DX =    0.0                 !
 ! A5    A(1,3,8)              109.6585         -DE/DX =    0.0                 !
 ! A6    A(2,3,5)              110.7232         -DE/DX =    0.0                 !
 ! A7    A(2,3,8)              109.657          -DE/DX =    0.0                 !
 ! A8    A(5,3,8)              123.9638         -DE/DX =    0.0                 !
 ! A9    A(1,4,2)               85.4222         -DE/DX =    0.0                 !
 ! A10   A(1,4,6)              110.7232         -DE/DX =    0.0                 !
 ! A11   A(1,4,7)              109.657          -DE/DX =    0.0                 !
 ! A12   A(2,4,6)              110.7247         -DE/DX =    0.0                 !
 ! A13   A(2,4,7)              109.6585         -DE/DX =    0.0                 !
 ! A14   A(6,4,7)              123.9637         -DE/DX =    0.0                 !
 ! D1    D(4,1,3,2)              1.1698         -DE/DX =    0.0                 !
 ! D2    D(4,1,3,5)            111.6113         -DE/DX =    0.0                 !
 ! D3    D(4,1,3,8)           -108.0837         -DE/DX =    0.0                 !
 ! D4    D(3,1,4,2)             -1.1699         -DE/DX =    0.0                 !
 ! D5    D(3,1,4,6)           -111.6129         -DE/DX =    0.0                 !
 ! D6    D(3,1,4,7)            108.0852         -DE/DX =    0.0                 !
 ! D7    D(4,2,3,1)             -1.1699         -DE/DX =    0.0                 !
 ! D8    D(4,2,3,5)           -111.6129         -DE/DX =    0.0                 !
 ! D9    D(4,2,3,8)            108.0852         -DE/DX =    0.0                 !
 ! D10   D(3,2,4,1)              1.1698         -DE/DX =    0.0                 !
 ! D11   D(3,2,4,6)            111.6114         -DE/DX =    0.0                 !
 ! D12   D(3,2,4,7)           -108.0838         -DE/DX =    0.0                 !
 --------------------------------------------------------------------------------
 GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The symmetry of all four isomers are shown in the tables above. A C₁ symmetry is also known as the identity operation (E), this operation returns the molecule back to its original orientation, hence it is trivial. The symmetry associated with isomers 3 and 4 is C_2v, which has the following symmetry elements E, C₂ and two vertical mirror planes. This can be rationalised by visualising the molecule in three dimensions.

It was noted that the disappearance of the bridging bonds in diagrams 13 to 16 was due to the fact that the optimisations for these bonds fell outside of the parameters set in Gaussview before the molecules were optimised.

Energies of the four Al₂Cl₄Br₂ isomers

**Energies of the four Al₂Cl₄Br₂ isomers (Table 28)**
Isomer 1	-237510 kJ mol^-1
Isomer 2	-237520 kJ mol^-1
Isomer 3	-237540 kJ mol^-1
Isomer 4	-237540 kJ mol^-1

As shown in table 28 above, the most stable isomer is isomer 3. All 4 isomers exhibit two 3-centre-4-electron bridging bond. 3-centre-4-electron bonds are known to be weak because four electrons are shared over three atoms instead of a conventional bond, where two electrons are shared between two atoms in a bond. Therefore, these bridging bonds are known to be weaker when compared to terminal bonds.

The isomers of Al₂Cl₄Br₂ tend to be most stable when the Br atoms occupy terminal positions. Al-Cl bonds are shorter and stronger when compared to Al-Br bonds, which are longer and weaker (shown in tables 22 and 24 above). Br has a larger atomic radii than Cl as Br has more electrons when compared to Cl. Therefore Br must be held further away from Al than Cl so as to avoid repulsive interactions with the Al atom. The strength of the Al-Cl-Al bridging bond contributes to the increased stability of both isomers 3 and 4 as compared to isomers 1 and 2, where Br atoms are in bridging positions. The strength of these bridging bonds are vital as these bonds hold the structure of the dimer in place.

Dissociation energy of isomer 3

The dissociation of Al₂Cl₄Br₂ (Isomer 3) into its respective monomers is shown in the following equation:

Al₂Cl₄Br₂ -> 2AlCl₂Br

The energies of each molecule in this reaction are shown below:

E(AlCl₂Br)= -45.22 au

E(Al₂Cl₄Br₂)= -90.47 au

The energy difference is given by ΔE = 2E(AlCl₂Br)-E(Al₂Cl₄Br₂), where ΔE is equal to 0.03 au which is equivalent to 80 kJ mol^-1. Hence the dissociation energy is 80 kJ mol^-1.

The difference in energy indicates that dissociation of isomer 3 is not favourable as the monomer AlCl₂Br is less stable as compared to the Al₂Cl₄Br₂ isomer, hence there is no driving force for the dissociation to occur spontaneously.

Frequency Analysis of all isomers

A frequency analysis was done using all four LanL2DZ optimised Al₂Cl₄Br₂ isomers on Gaussian 5.0.

Frequency Analysis of isomer 1

The log file for the frequency analysis of isomer 1 can be found here. File:QLOAL2CL4BR2FREQUENCY2.LOG

**Frequency analysis of Isomer 1 (Table 29)**
File Name	QLOAL2CL4BR2FREQUENCY2
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.46 a.u.
RMS GRADIENT NORM	0.000000200 a.u.
Imaginary Freq	0
Dipole Moment	0.00 Debye
Point Group	D_2h

Low frequencies ---   0  0   0  0    0    0
 Low frequencies ---   15.8928   52.6131   72.9783

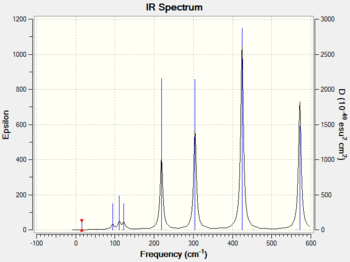
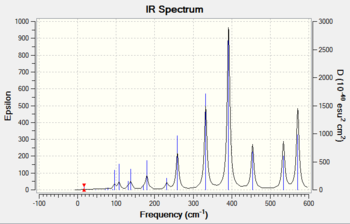
The frequency analysis was carried out correctly as there was no observable change in the energy of the molecule. A minimum was obtained as there are no negative frequencies. An IR spectrum of isomer 1 was computed as a result of the frequency analysis and the result is shown in diagram 17 below.

Frequency analysis of isomer 2

The log file for this analysis can be found here. File:QLOISOMER2FREQ.LOG

**Frequency analysis of Isomer 2 (Table 30)**
File Name	QLOISOMER2FREQ
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.47 a.u.
RMS GRADIENT NORM	0.000000095 a.u.
Imaginary Freq	0
Dipole Moment	0.84 Debye
Point Group	C₁

Low frequencies ---    0    0    0    1    1    2
 Low frequencies ---   16.9743   46.4585   71.6723

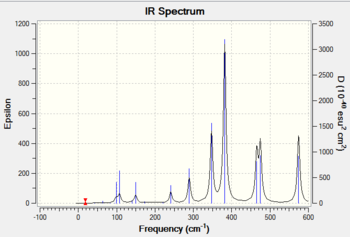
The frequency analysis was carried out correctly as there was no observable change in the energy of the molecule. A minimum was obtained as there are no negative frequencies. An IR spectrum of isomer 2 was computed as a result of the frequency analysis and the result is shown in diagram 18 below.

Frequency analysis of isomer 3

The log file for this analysis can be found here. File:QLOISOMER31FREQ.LOG

**Frequency analysis of Isomer 3 (Table 31)**
File Name	QLOISOMER31FREQ
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.47 a.u.
RMS GRADIENT NORM	0.000000085 a.u.
Imaginary Freq	0
Dipole Moment	0.89 Debye
Point Group	C_2v

Low frequencies ---   0    0   0    1    1    2
 Low frequencies ---   18.2819   42.1474   64.3213

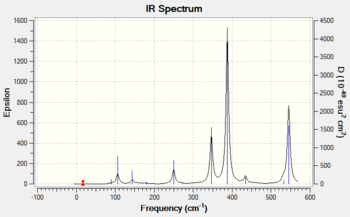
The frequency analysis was carried out correctly as there was no observable change in the energy of the molecule. A minimum was obtained as there are no negative frequencies. An IR spectrum of isomer 3 was computed as a result of the frequency analysis and the result is shown in diagram 19 below.

Frequency analysis of isomer 4

The log file for this analysis can be found here. File:QLOISOMER4FREQ.LOG

**Frequency analysis of Isomer 4 (Table 32)**
File Name	QLOISOMER4FREQ
File Type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis Set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-90.47 a.u.
RMS GRADIENT NORM	0.000000097 a.u.
Imaginary Freq	0
Dipole Moment	0.96 Debye
Point Group	C_2v

Low frequencies ---   0    0    0    1    2    3
 Low frequencies ---   17.4807   42.2309   69.7909

The frequency analysis was carried out correctly as there was no observable change in the energy of the molecule. A minimum was obtained as there are no negative frequencies. An IR spectrum of isomer 4 was computed as a result of the frequency analysis and the result is shown in diagram 20 below.

Discussion of the computed IR spectra of all four isomers

An IR band is only active when absorption of infrared light results in a change in the overall dipole moment of the molecule. The intensity of these bands are directly related to the change in dipole moment, where the more polar the bond, the more intense the IR band will appear on the spectrum. Vibrations involving symmetrical bonds are said to be IR inactive as it does not lead to a change in the overall dipole moment of the molecule.

Isomer 2 has a C₁ symmetry, which is also known as the identity operation (E). This operation returns the molecule back to its original orientation which makes this molecule asymmetric. This asymmetric property explains why this isomer produced an IR spectrum with the most number of peaks as compared to the other isomers (1,3 and 4).

All four isomers here are non-linear and which means they have 3N-6 vibrational degrees of freedom. However, as shown in diagrams 17-20 above, the number of peaks in each IR spectrum are less than the number of vibrational modes (18) in each isomer. This can be attributed to the fact that certain vibrational modes are degenerate or have the same energy, which accounts for the fewer number of peaks seen in diagrams 17-20.

The four isomers have different point groups as shown in the previous section, which explains why the IR spectra of all four isomers appear different. Different point groups will have vibrations with different symmetries, which will affect both the frequency (or energy) and the intensity of the band in IR spectrum.

Discussion of the Al-Br stretching vibrations

In this section, comparisons are made between similar vibrational modes of different isomers. Only key vibrational modes are considered here.

**Vibrational analysis (Table 33)**
Row	Isomer	Mode	Frequency (cm^-1)	Intensity	Isomer	Mode	Frequency (cm^-1)	Intensity
1	1	13	230	0	4	16	434	21
2	1	12	219	118	4	12	250	40
3	1	13	230	0	3	16	465	95

Vibrational mode 13 in isomer 1 has an intensity of zero as it is an IR inactive stretch. There was no observable change in dipole moment as the vibrational mode is symmetrical as shown in the table above.

Vibrational modes (12 and 13) in isomer 1 has bridging Br atoms which exhibits a lower frequency when compared to vibrational modes (12 and 16) in isomer 4, which has terminal Br atoms. This could be rationalised by taking into account the strength of terminal Al-Br bonds which are stronger than the electron deficient bridging three-centre-four-electron Al-Br-Al bonds.

Vibrational mode 13 in isomer 1 has bridging Br atoms which has weak Al-Br-Al bridging bonds, hence this vibrational mode has a lower frequency when compared to vibrational mode 16 in isomer 3. This isomer contains terminal Al-Br bonds which are stronger and therefore it has a higher frequency vibrational mode even though both vibrational modes are similar in terms of the motion of all the atoms in the molecule.

The heavy atom effect also plays a part in the frequency of the vibrational modes. A heavier atom such as Br will cause the bond to absorb IR light at a lower frequency. This heavy atom effect was explained earlier in this report using the following equations:

where k is the spring constant for the Al-Br bond, c is the speed of light and μ is the reduced mass of the Al-Br bond, which is given by equation 2 below:

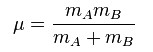
where m_A is the mass of atom A and m_B is mass of atom B.

As shown by the two equations above, a heavy atom will lead to an increase in the reduced mass which is inversely proportional to the frequency of the vibration.

MO calculations

MO calculations were carried out on the lowest energy isomer, which in this case is isomer 3. The .chk file from the optimisation of isomer 3 was used together with the keywords "pop=full" for NBO analysis. The file for this analysis can be found here. File:Qloisomer31.chk

In this MO calculation, only non-core orbitals are visualised and out of these orbitals, 5 MOs were chosen ranging from highly bonding to highly antibonding were chosen for further analysis. These MOs are shown in the diagrams below.

Diagram 21: MO 17 of isomer 3, where the interactions indicate that this is a bonding MO. The bonding interactions between AOs cancels out the antibonding interactions which are moderate at best. The antibonding interactions between the Cl p-orbitals are moderate due to non-ideal orbital overlap between these two orbitals. The AOs of the terminal Cl atoms are delocalised over three atoms, indicating a strong bonding interaction between Cl-Al-Cl bond and also the presence of interactions between the two terminal Cl atoms. AO interactions in this MO are mainly through space interactions as shown above. There are a total of 6 nodes in this MO where 2 of them are hidden.

Diagram 22: MO 18 of isomer 3, where the interactions indicate that this is a bonding MO. The bonding interactions are significantly stronger when compared to the antibonding interactions in this MO. The partial delocalisation of AOs between 2 terminal Cl atoms shown above gives credence to the idea that interactions between terminal Cl atoms are present. However in this case, the overlap between the terminal Cl AOs are not as good due to the orientation of the AOs relative to each other. AO interactions are predominately through space interactions. There are a total of 4 nodes in this MO.

Diagram 23: MO 19 of isomer 3, where the interactions indicate that this is an antibonding MO. Only antibonding through space interactions are present in this MO. This MO is not delocalised as we can see above. A node is present between terminal Cl p-orbitals because both p-orbitals are orientated in such a way that the wavefunction of each p-orbital perfectly cancels out and goes to zero. The same can be said for both p-orbitals of the bridging Cl atoms. There are a total of 6 nodes in this MO, where 2 of them are between AOs as shown above.

Diagram 24: MO 20 of isomer 3, where the interactions indicate that this is a moderately antibonding MO. Bonding through space interactions are present between the bridging Cl atoms in this MO, which are hidden in this diagram. The p-orbitals of the terminal Cl atoms are not completely out of phase due to their orientation relative to each other, hence a node is not present in this case. The antibonding through space interactions are slightly stronger than the bonding interactions mainly due to the proximity of the terminal p-orbitals, where strong through space antibonding interactions are present. There are a total of 4 nodes in this MO, where 2 of them are hidden.

Diagram 25: MO 24 of isomer 3, where the interactions indicate that this is an antibonding MO. The antibonding interactions in this MO are stronger than the bonding interactions, cancelling out the effect of the bonding interactions in the process. As with MO 20 shown in diagram 24, the p-orbitals of the terminal Br atoms are not completely out of phase due to their orientations with respect to each other, hence a node is absent between these two orbitals. MOs 20 and 24 share many similar characteristics with the exception of the fact that there are interactions between the p-orbitals of terminal Br atoms and not terminal Cl atoms and the other exception is the weaker through space bonding interaction between bridging Cl atoms in MO 24 as compared to the one in MO 20, which makes MO 24 more antibonding than MO 20. There are a total of 4 nodes in this MO.

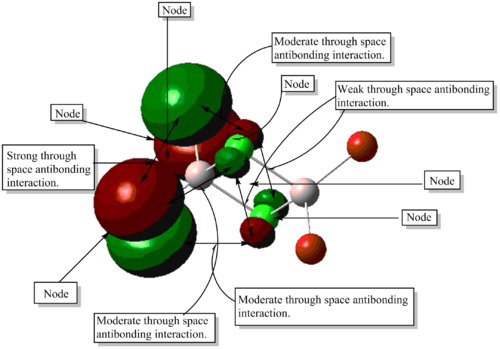
MO calculations of isomer 3 indicated the presence of 116 frozen core electrons, where 24 MOs were fully occupied by a pair of electrons with opposite spins due to Hund's rule and the Pauli exclusion principle. A brief visualisation of all 24 MOs including both core and non-core MOs showed the absence of bonding or antibonding interactions between the AOs of Al. It was concluded that an Al-Al bond does not exist, as evidenced by the presence of a node between two Al AOs in diagram 26.

Both bonding and antibonding interactions in the 5 non-core MOs shown above were mostly through space interactions. Which suggests that the AlCl₄Br₂ isomer is held together by these moderate to weak through space interactions. When these interactions are taken into account as a whole, they are considerably strong which prevents the isomer from breaking up into AlCl₂Br monomers.

There are no pi-bonds present in this isomer, as evidenced by the MO calculations and the MOs shown in diagrams 21-25 above. There were no sideways overlap of p-orbitals between adjacent atoms in the dimer in both core and non-core MOs. However, there are some form of interaction between the p-orbitals between terminal Cl and Br atoms as shown above, these interactions are also known as pi-type interactions. Pi-type interactions are vital to biological systems where common pi-interactions include metal-pi interactions and polar-pi interactions.

Larger than usual energy gaps (approximately 0.20 au) were observed between non-core MOs 24-25 and between core MOs. This suggests MO mixing might have occurred. MO mixing occurs when the MOs involved in mixing have the same symmetry and are close in energy. However, this cannot be verified as the MO calculations alone did not provide the symmetry of each individual MO.

Summary

In general, the computed properties of molecules investigated in both parts 1 and 2 using Gaussview 5.0 were in good agreement with the experimentally reported values and it was observed that using higher basis sets such as LanL2DZ led to better results. However, it was not possible to determine the accuracy of MO theory in the prediction of real MOs of more complex molecules as the molecules analysed here are rather simple (i.e. BH₃ and NH₃). Further analysis of more complex molecules could have been done as part of this experiment to determine the efficacy of this theory.

References

↑ ^1.0 ^1.1 K. Kawaguchi , J. Chem. Phys., 1992, 96, 3411
↑ ^2.0 ^2.1 D. Oxtoby, H. Gillis and A. Campion , Principles of Modern Chemistry, 2011, 274
↑ Q. Lo, Gaussian Job Archive Br3Ga1, 2014 ; DOI:10042/27634
↑ C. Da Silva, O. Proux, J-L. Hazemann, J. James-Smith, D. Testemale and T. Yamaguchi , J. Mol. Liq., 2008, 147, 83-95.
↑ ^5.0 ^5.1 W. M. Hayes and D. R. Lide, CRC Handbook of Chemistry and Physics, 2013, 94.
↑ Q. Lo,Gaussian Job Archive B1Br3, 2014 ; DOI:10042/27636
↑ ^7.0 ^7.1 G. Santiso-Quinones and I. Krossing, Z. Anorg. Allg. Chem., 2008, 634, 704-707.
↑ T. L. Cottrell , The Strength of Chemical Bonds, Butterworths, 1958, 2
↑ S. W. Benson , J. Chem. Educ., 1965, 42, 502.
↑ P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, 2009, 9.
↑ J. W. Ochterski, Vibrational Analysis in Gaussian, 1999.
↑ A. Haaland , Angew. Chem. Int. Ed. Engl., 1989, 28, 992-1007.

[kawa-1] 1.0 ^1.1 K. Kawaguchi , J. Chem. Phys., 1992, 96, 3411

[oxtoby-2] 2.0 ^2.1 D. Oxtoby, H. Gillis and A. Campion , Principles of Modern Chemistry, 2011, 274

[qlo1-3] Q. Lo, Gaussian Job Archive Br3Ga1, 2014 ; DOI:10042/27634

[silva-4] C. Da Silva, O. Proux, J-L. Hazemann, J. James-Smith, D. Testemale and T. Yamaguchi , J. Mol. Liq., 2008, 147, 83-95.

[CRC-5] 5.0 ^5.1 W. M. Hayes and D. R. Lide, CRC Handbook of Chemistry and Physics, 2013, 94.

[qlo2-6] Q. Lo,Gaussian Job Archive B1Br3, 2014 ; DOI:10042/27636

[santiso-7] 7.0 ^7.1 G. Santiso-Quinones and I. Krossing, Z. Anorg. Allg. Chem., 2008, 634, 704-707.

[Cottrell-8] T. L. Cottrell , The Strength of Chemical Bonds, Butterworths, 1958, 2

[Darwent-9] S. W. Benson , J. Chem. Educ., 1965, 42, 502.

[Atkins-10] P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, 2009, 9.

[ochterski-11] J. W. Ochterski, Vibrational Analysis in Gaussian, 1999.

[Haaland-12] A. Haaland , Angew. Chem. Int. Ed. Engl., 1989, 28, 992-1007.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]