Rep:Mod:indoranyon

Introductory Exercises

BH₃

Basic calculations

Having followed the instructions for creating and optimising a borane molecule, the optimum B-H bond distance was found to be 1.19 Å and the H-B-H bond, 120°.

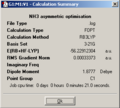
From the program summary:

file type = .log

calculation type = FOPT

calculation method = RB3LYP

basis set = 3-21G

final energy = -26.5 au

dipole moment = 0

point group = D_3h

calculation time = 21 s

The same steps being followed for BCl₃, the following information was found:

B-Cl distance = 1.78 Å

Cl-B-Cl angle = 120°

file type = .log

calculation type = FOPT

calculation method = RB3LYP

basis set = 3-21G

final energy = -1398.8 au

dipole moment = 0

point group = D_3h

calculation time = 25 s

Vibrational analysis

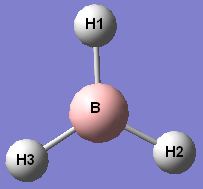
Frequency analysis was carried out on the BH₃ molecule. The predicted IR spectrum was obtained and the following table of modes and frequencies drawn up - the atoms are numbered as shown in the diagram to the right.

Table of predicted vibrational frequencies for BH₃

no.	mode	frequency	intensity	symmetry
1	H atoms vibrate up and down relative to plane of molecule	1145.71	92.70	A2’’
2	H2 & H3 bending, in plane	1204.66	12.38	A1’
3	H1 bending, in plane	1204.66	12.38	A2’
4	H atoms stretching, in plane & in phase	2592.79	0	A1’
5	H2 & H3 stretching in plane & in antiphase	2731.31	103.84	A2’
6	H1 stretching in antiphase with H2 & H3	2731.31	103.83	A1’

Looking at the table it is easy to see why there are only three peaks in the spectrum; only vibration 1 has a unique frequency. Vibrations 2 & 3, and 5 & 6 occur at exactly the same point in the spectrum and so their peaks overlap, while as vibration 4 has an intensity of 0 it will not give rise to a peak at all.

Molecular orbitals

MO diagram of borane

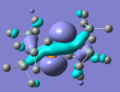
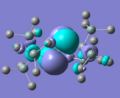
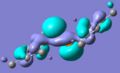
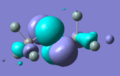
MO diagram drawn, and Gaussian used to create models of the molecular orbitals of BH₃. The HOMO and LUMO from both these methods are shown below; the close agreement indicates that basic, qualitative MO theory is a good method of estimating the shapes of orbitals, at least for this type of small, fairly simple structure.

HOMO

LUMO

A small molecule

The molecule selected was P(CN)₃. This was built in GaussView and optimised initially in the same way as the previous structures. This was then submitted to SCAN for a more thorough optimisation; the results were saved in ‘D-space’ and can be found here: DOI:10042/to-1253 . The results from both of these optimisations were the same which indicates that the previous, more basic method works well for small molecules.

Atom coordinates for P(CN)₃

centre number	atomic number	atomic type	X	Y	Z
1	15	0	0.000000	0.000000	0.000000
2	6	0	0.000000	1.732952	0.000000
3	6	0	1.500781	-0.866476	0.000000
4	6	0	-1.500781	-0.866476	0.000000
5	7	0	2.513316	-1.451064	0.000000
6	7	0	-2.513316	-1.451064	0.000000
7	7	0	0.000000	2.902128	0.000000

P-C distance = 1.73 Å

C-N distance = 1.17 Å

C-P-C angle = 120°

calculation method = RB3LYP

basis set = 3-21G

final energy = -616.5 au

dipole moment = 0

point group = D_3h

calculation time = 36 s

Isomers of an organometallic complex

Using L=P(CH₃)₃. Settings when submitted to SCAN for first optimisation: # B3LYP/B3LYP/3-21G* opt=loose

Settings for second optimisation: # B3LYP/LANL2DZ opt int=ultrafine scf=conver=9.

As suggested, the advanced options for including the d-orbital functions were explored. The settings for this final optimisation were: # opt b3lyp/lanl2mb geom=connectivity extrabasis. However, when opened in Gaussview, the optimisation had apparently removed the Mo-P bonds. Possibly this is due to inclusion of d-orbital character rendering these bonds less simply covalent in nature. Both the second optimisation and these structures were used for frequency and geometry analysis; the spectra, however, are very similar, as there are only three modes of vibration which give rise to notable peaks. The same for both isomers, these are: Mo-C-O ‘wagging’, with the C atoms moving the most, at around 550; C-H bending around 1200; and C-O stretching at 2000-2250.

The first vibration is slightly lower in energy, lower intensity, and less diffuse in the case of the cis-isomer, but none of these differences are particularly striking. The C-H bending vibrations are even more alike, which is unsurprising given that these molecules differ only in the relative placement of their C=O groups – in the cis-isomer some of the methyls will be closer together; however, this does not impact the motion of the hydrogen atoms. The C-O stretching peaks differ only very slightly in wavenumber, and the noticeable difference in intensity may be attributed to the fact that in the trans-isomer, both of the stretches (each set of two ligands gives rise to its own peak) are of the exact same energy. This is as expected, and causes an overlap which decreases the apparent intensity of the signal. Looking at the numerical output however, these signals are very close in intensity to the more intense of the two cis-isomer peaks. In this isomer, the peaks differ, as the ligand environments are no longer equivalent; the peak associated with the two ligands trans- to each other is significantly more intense than that of the two that are cis. This is likely due to the trans-effect, which tends to be very noticeable with carbonyl ligands.

The results of the final set of calculations can be found here:

Trans-isomers: without d-orbitals DOI:10042/to-1285 ; with d-orbitals included DOI:10042/to-1286

Cis-isomers: without d-orbitals DOI:10042/to-1284 ; with d-orbitals included DOI:10042/to-1283

The spectra and structures of the two isomers are provided below.

• 
  Spectrum of cis-isomer
• 
  Spectrum of trans-isomer

Structure of cis-isomer

Structure of trans-isomer

Ammonia

Molecule generated, optimised using the same method as for BH₃ / P(CN)₃. Point group was, indeed, C_3v. Optimising a molecule with one bond longer than the rest, the point group was C₁. With restricted symmetry, D_3h.

• results summaries for the three geometries of ammonia
• 
  C_3v
• 
  C₁
• 
  D_3h

The final structure was obviously changed by the symmetry; the very highly symmetric D_3h structure is planar, compared to the ‘puckered’ shapes of the other two. The time taken for a calculation, however, only seems to be significantly affected in the case of the D_3h structure – likely the number of symmetry operations possible on this structure, in comparison to the others, increases the amount of calculation necessary to optimise its geometry. Thus a structure with a very high symmetry – for example, an octahedral complex with eight identical ligands – would take a long time to optimise.

The energies of all three structures are very similar – the C_3v has very slightly lower energy than the C₁, making it the second lowest-energy geometry after D_3h – however the differences are slight, as the structural differences are not very great. Notably, however, the difference between the energies of the D_3h (flat) and C₁ structures is much greater than that between C₁ and C_3v (both puckered); this is significant, as this flat shape is the transitional state which ammonia undergoes when it inverts from one geometry to the other, passing over a potential barrier. Here, the results indicate that this state is actually more stable than either of the end structures, which seems implausible – this is most likely due to the fact that when dealing with such small differences, this basis set is not fine enough.

Energy of the potential barrier

As instructed, the shapes of the normal C_3v ammonia molecule and the planar transition state were optimised. These were more accurate, with better basis sets; the calculations took correspondingly longer, and the energies produced were slightly different – in this set, the expected pattern of the transition state having the higher energy is seen. It is the difference in energy between the C_3v and the D_3h structures which gives the potential barrier to ammonia’s inversion.

C_3v: -56.58263593 au

D_3h: -56.42664911 au

ΔE = 0.155987 au = 410 kJmol^-1

The experimentally determined value is 24.3 kJmol^-1; the great difference between these results and what was experimentally determined is either to do with a calculation error (though the procedure was repeated, and the same results obtained) or to do with the fact that using this method, the energy for one molecule’s inversion was calculated, and multiplied by Avogadro’s constant. This clearly assumes that each molecule acts entirely independently, which is probably not the case. Ammonia is potentially vulnerable to a great deal of inter-molecular interaction and it may be that some of this interaction acts to stabilise the transition state, thus lowering the potential barrier.

Vibrational analysis

Spectrum of C_3v NH₃

The IR spectra of C_3v and D_3h NH₃ are shown to the right. They are fairly similar to that of BH₃ (calculated earlier) which is not surprising; though the frequencies at which these vibrations occur are rather different, the C_3v shares with BH₃ a relatively intense H-wagging peak, appearing at the low end of the spectrum. The next peak (actually a pair of degenerate peaks) on both is much lower, and corresponds to the sideways rocking of the H-atoms (in BH₃, this happens in the molecule’s plane). The only striking difference is in the stretching vibrations. In NH₃, all three of these peaks are negligable, whereas in BH₃ only the perfectly symmetrical, in-phase stretching has an intensity of zero; the asymmetric, out-of-phase stretching vibrations give rise to a pair of degenerate peaks. This can be attributed to the difference in symmetry as the NH₃ transition state, which shares the symmetry of BH₃, shows a pattern of intensities which is a curious mix of the two molecules’ – though the last two peaks are noticeable, and degenerate, in the style of BH₃ they are (relative to the first peak) very small. This suggests that NH₃ does not favour in-plane hydrogen stretching vibrations (perhaps because the molecule’s natural shape is not planar) but the symmetry of the transition state causes sufficient vibrations to appear on a spectrum.

Spectrum of D_3h NH₃

The second interesting feature of the D_3h ammonia spectrum is that it contains a single negative peak, occurring at -318. This is characteristic of a transition state and in this case, corresponds to the out-of-plane hydrogen ‘wagging’ vibration. Given that the inversion of ammonia proceeds via this type of ‘umbrella opening’ mechanism, it can be deduced that this is the vibration which ‘follows’ the inversion path – a conclusion supported by the overwhelmingly high intensity of this peak in the spectrum.

Mini-project: Stabilisation of Phosphorus-Phosphorus Double Bonds

In the second year 'Main Group Chemistry' lecture course, it was briefly explained that elements such as phosphorus and sulphur prefer to catenate than to form homonuclear double bonds; and that these bonds can generally only be formed via kinetic stabilisation with very bulky ligands. I found this very interesting and so decided to focus this mini-project on this idea. I will be attempting to answer the question, Can I predict whether a P-P double bond, in a given structure, will be stable?. First I will look at two known stable compounds (specifically, bond lengths, MO's and vibrational spectra - though ³¹P NMR would be useful the methods outlined for NMR predictions are described as 'unsuitable for inorganic molecules') and one known unstable one, hopefully finding some common features which can then be applied to two unknown structures (these will be generated by removing some of the bulk from the known-stable molecules).

Stable molecules

bis(2,4,6-tri-tert-butylphenyl) diphosphene

bis(2,4,6-tri-tert-butylphenyl) diphosphene

This structure, reported by Yoshifuji et al in 1981, is one of the earliest examples of a P-P double bond. When constructing this structure (and all the others) the key bond lengths and angles were set to those reported in the referenced paper:

P-P = 2.034 Å

P-C = 1.862 Å

P-P-C = 102.8°

C-P-P-C = 172.2°

Although later it was found that the bond lengths had been optimised to be longer than this, and the angles somewhat more acute (this bond-lengthening was common to all of the structures studied). In this case, the P-P bond distance was found to be 2.17 Å, which although longer than what was expected, is still shorter than the 2.21-2.22 Å reported for a P-P single bond.

Vibrational spectrum of bis(2,4,6-tri-tert-butylphenyl) diphosphene

Shown to the right is the predicted vibrational spectrum of this molecule. The key vibration - P-P stretching - is too low intensity to be visible here. However, it is a clear and unique vibration, ocurring at 558 cm^-1. This is somewhat lower than the 580 - 600 cm^-1 range reported for the P-P double bond stretching; however, it accords well with the longer-than-expected bond lengths, and can probably be reported as a systematic feature rather than failure in this specific case.

The settings used for the optimisations of this structure (the others were the same) were: # opt b3lyp/3-21g geom=connectivity extrabasis - d-orbitals were judged to be important in this case, and were included. The optimisation report can be found here: DOI:10042/to-1368 .

• MO's of bis(2,4,6-tri-tert-butylphenyl) diphosphene (H's removed for clarity)
• 
  HOMO
• 
  LUMO

The HOMO and LUMO generated for this structure are shown above. It is mentioned in the literature that the LUMO of a stable diphosphene is the P-P π* orbital, and here this is certainly the case - if this pattern of orbitals repeats in the other stable molecule it will be something to look for when deciding the stability of unknown structures.

bis-tris-(trimethylsilyl)methyl diphosphene

bis-tris-(trimethylsilyl)methyl diphosphene

Optimisation report: DOI:10042/to-1369 .

Optimised bond lengths and angles:

P-P = 2.17 Å

P-C = 1.94 Å

P-P-C = 106.2°

C-P-P-C = 179.1°

This shares the P-P distance of the other stable structure, which suggests quite strongly that they are of the same type. If this is assumed to be the length of a P-P double bond (at least, such a bond when calculated with this method) it would provide a quick and easy way to judge whether a structure is likely to be stable or not.

Vibrational spectrum of bis-tris-(trimethylsilyl)methyl diphosphene

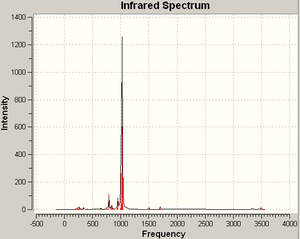
As above, the P=P stretching vibration has too low an intensity to be visible. In this case it is at 556 cm^-1; the common features of these stable molecules are a single, very low-intensity vibration around 550 - 560 cm^-1. Contrasting these characteristics with the vibrations of the unstable molecule (examined below) should help to decide whether a given structure is stable, or not.

• MO's of bis-tris-(trimethylsilyl)methyl diphosphene (H's removed for clarity)
• 
  HOMO
• 
  LUMO

The HOMO and LUMO here are the same as in the other stable molecule; evidence that this pattern is worth looking out for.

Unstable structure: 'phosphobenzene'

'phosphobenzene'

Optimisation report: DOI:10042/to-1372 .

P-P = 2.36 Å

P-C = 1.89 Å

P-P-C = 180°

C-P-P-C = -38°

As expected, here the P-P bond distance is considerably longer than the range predicted for even a single bond. The contrast between this length and the shorter one reported above should provide a rough estimate as to a molecule's stability.

Vibrational spectrum of 'phosphobenzene'

In this spectrum there are three calculated P-P stretches, all of which have an intensity of zero. The strongest (that is, the one in which the phosphorus atoms are the most displaced) is at 424 cm^-1; the other smaller ones are at 155 and 706 cm^-1. None of these are within the reported or experimental range for a P-P double bond stretch. Although these second two are more complex vibrations, involving the entire molecule, in the stable structure analysed above there was only one vibration involving a P-P stretch at all.

Interestingly, it did not seem to be possible to obtain MO's for this molecule; various error messages and several program crashes were obtained, and even when the file was importable into Gaussview, the 'visualize' tab was greyed out. Either the optimisation file was somehow corrupt or incorrect, or Gaussian is unable to create MO's for structures that do not strictly exist.

Unknown molecules

structure (a) - bis(2,4,6-trimethyl) diphosphene

'(a)'

Optimisation report: DOI:10042/to-1370 .

P-P = 2.16 Å

P-C = 1.90 Å

P-P-C = 99°

C-P-P-C = -180°

Although not sufficient to decide stability, the close agreement between the P-P bond length of this structure and the stable bis-tris-(trimethylsilyl)methyl diphosphene does support the conclusion that this molecule is a viable one.

Vibrational spectrum of bis(2,4,6-trimethyl) diphosphene

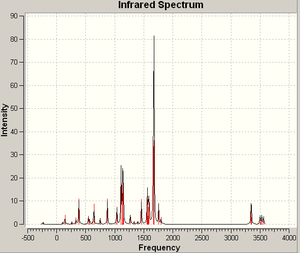
The two P-P stretching vibrations in this predicted spectrum are again, not visible. Importantly however their intensities are not zero. They ocurr at 523 and 590 cm^-1, one of which is well below the expected range and the other which is well within it. This mix of the characteristics of the stable and unstable molecules suggests that although this structure may not be entirely viable at room temperature, it does possess a degree of stability; it could be that it exists in equilibrium between the double-bonded state and, for example, a dimer with only single bonds between phosphorus atoms.

• MO's of bis(2,4,6-trimethyl) diphosphene (H's removed for clarity)
• 
  HOMO
• 
  LUMO

Given the apparent impossibility of obtaining MO's for the unstable molecule, the existence (as well as the form) of the HOMO and LUMO shown above is another argument in favour of this structure's viability. The HOMO is of the same form as the corresponding orbitals in the known stable molecules, and the LUMO is clearly the P-P π* orbital, which as mentioned is characteristic of stable diphosphenes. Based on this, the spectrum, and the details of the central bonds, it seems reasonable to suppose that this structure contains a fairly stable phosphorus-phosphorus double bond. Unfortunately, the literature is silent on this matter, and so independent corroboration is difficult.

structure (b) - bis-trisilylmethyl diphosphene

'(b)'

Optimisation report: DOI:10042/to-1371 .

P-P = 2.17 Å

P-C = 1.93 Å

P-P-C = 103.1°

C-P-P-C = 180°

As for structure (a), based merely off these bond lengths and angles it would be suggested that this was a stable molecule; these values are strikingly similar to those calculated for this molecule's 'parent compound', bis-tris-(trimethylsilyl)methyl diphosphene. Given how closely related the structures are this is not surprising but it provides strong evidence for stability.

Vibrational spectrum of bis-trisilylmethyl diphosphene

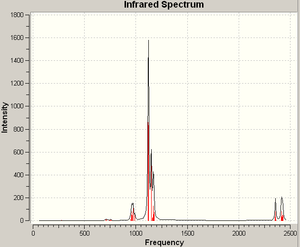
Here too this structure shows itself to be very similar to its parent (more similar to its parent than (a) above). There is one unique P-P stretching vibration, at 560 cm^-1, with an intensity too low to show on the spectrum. In comparison to structure (a) above it can be reasonably supposed that this is the more stable molecule, existing in a single state (not in equilibrium).

• MO's of bis-trisilylmethyl diphosphene (H's removed for clarity)
• 
  HOMO
• 
  LUMO

This case is much the same as structure (a) above - the HOMO is the characteristic shape, the LUMO is the P-P π*, and the energies given by Gaussview are about the same as for the parent (around -0.11 - -0.12 for the HOMO, and 0.035 - 0.045 for the LUMO); and so the same basic conclusion is drawn: this is a stable diphosphene. However, based on the vibrational data, I would suggest that this is the more stable of the two and unlike (a) does not exist in equilibrium. Again, unfortunately, literature reports of this are impossible to find.

Although this has been interesting to work on, there is still an obvious line of questioning that could be pursued: namely, if I continued to shrink the ligands on the two 'parents' used here (and others), and what point will the molecules produced become unquestionably unstable? The possibility of including heteroatoms, and perhaps coming to a general conclusion, seems like a very interesting one.