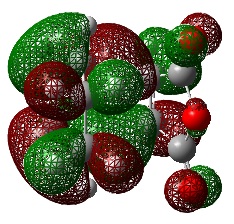
Rep:Mod:imissmelody

In this set of computational experiments, the transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions was characterised.

In this experiment, molecular orbital-based methods were used, by numerically solving the Schrodinger equation, and locating transition structures based on the local shape of a potential energy surface. As well as showing what transition structures look like, reaction paths and barrier heights can also be calculated.

For this wiki page, please click on the Jmol app button to open a new window of the Molecular Structure. GIF files displaying vibrational modes may not automatically play due to the size of the file, so open the file in a new window, and click on the file in the new window to play the vibrational animation.

The Cope Rearrangement

In the first part of this computational experiment, the Cope rearrangement of 1,5-hexadiene was studied. The objectives are to locate the low-energy minima and transition structures on the C6H10 potential energy surface, to determine the preferred reaction mechanism. This [3,3]-sigmatropic shift rearrangement has been the subject of numerous experimental and computational studies, and for a long time its mechanism (concerted, stepwise or dissociative) was the subject of controversy. It is now generally accepted that the reaction occurs in a concerted fashion via either a "chair" or a "boat" transition structure, with the "boat" transition structure lying several kcal/mol higher in energy. The B3LYP/6-31G* level of theory has been shown to give activation energies and enthalpies in remarkably good agreement with experimental values, and this will be carried out in this computation using Gaussian.

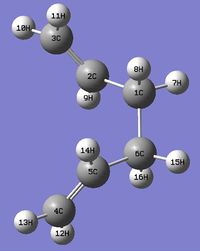
1,5-hexadiene

Optimization of Antiperiplanar 1,5-hexadiene (Anti 2 Conformer)

Optimised 1,5-hexadiene Molecule Summary File Type & Link .log Calculation Type FOPT Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.69254 Gradient (au) 0.00001891 Dipole Moment (Debye) 0.00 Symmetry Point Group C1 CPU Calculation Time (s) 26.0

Item Value Threshold Converged? Maximum Force 0.000060 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000516 0.001800 YES RMS Displacement 0.000171 0.001200 YES Predicted change in Energy=-2.036802D-08 Optimization completed. -- Stationary point found. A 1,5-hexadiene conformer where the 4 central carbon atoms are all antiperiplanar (app) to each other was created using Gaussview. The conformer was optimized using the the Hartree Fock method with a low level 3-21G basis set. The RMS Energy Gradient was below 0.001, which shows that the conformer was successfully optimized to a minimum/maximum in the Potential Energy Surface. This is also confirmed by the convergence of the force and displacement calculated. Further frequency analysis to confirm the minimum nature in the PES was carried out in a later section. Initially, the calculated conformer had a C1 symmetry, however, after "Symmetrize" operation, the conformer was found to have a Ci symmetry, with a point of inversion in between the 2 central C nuclei. The conformer was identified as the Anti 2 Conformer based on this table.

Optimization of Gauche 1,5-hexadiene (Gauche 3 Comformer)

Optimised Gauche 3 Conformer Summary File Type & Link .log Calculation Type FOPT Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.69266 Gradient (au) 0.00000851 Dipole Moment (Debye) 0.00 Symmetry Point Group C1 CPU Calculation Time (s) 44.0

Item Value Threshold Converged? Maximum Force 0.000027 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000402 0.001800 YES RMS Displacement 0.000172 0.001200 YES Predicted change in Energy=-7.448713D-09 Optimization completed. -- Stationary point found. In comparing the relative stabilities of gauche and app conformations, three effects need to be considered; the effect of stabilising σC-H → σ*C-H and σC-C → σ*C-C orbital interactions, the Pauli repulsion energy, and Van Der Wall's Forces. In n-butane, the first two favor the app conformation. However, in gauche 1,5-hexadiene, the vinyl hydrogen nuclei are separated by 2.5 A while in the case of n-butane the hydrogen nuclei separation is 2.35 A. As such, the H nuclei in gauche 1,5-hexadiene experience less steric repulsion, resulting in a gauche conformer that is relatively more stable and lower in energy. Thus, it was expected that the gauche conformer would be comparable in energy with the app conformer. In fact, when a gauche 1,5-hexadiene conformer was optimized, it was found that its energy was actually lower than the app conformer. This is unexpected stabilization is predicted to be due to an attractive interaction between the π orbital and the vinyl proton. The calculated conformer had a C1 symmetry, even after a "Symmetrize" operation. The conformer was identified as the Gauche 3 Conformer based on this table.

Optimization of Lowest Energy Conformer Prediction of 1,5-hexadiene

Attractive interaction between the π orbital and the vinyl proton.

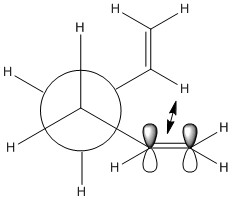If predictions were made based on prior knowledge on conformational behavior of alkanes, one would assume that the conformer with the most anti-periplanar interactions and least steric and Pauli repulsion would be the most stable. However, as shown in the Gauche 3 conformer optimization, this is certainly not true for 1,5-hexadiene. The diminished steric repulsion between hydrogen atoms leave the attraction between the π orbital and the vinyl proton to be the major interaction. Thus, maximizing this interaction would result in the lowest energy conformer. However, all conformers where this interaction is possible are just enantiomers of the Gauche 3 conformer. Thus, the lowest energy conformer would be the Gauche 3 conformer found above, as proven in literature and this table.

Optimization of 1,5-hexadiene Anti 2 Conformer with a Higher Basis Set

An Anti-2 Conformer has already been optimized using the HF/3-21G basis set shown above. However, the HF/3-21G basis set is a very low level basis set and is prone to inaccuracy although it has a fast calculation time. To increase the accuracy of the computation, a higher level B3LYP/6-31G* basis set will be used instead. Before this calculation however, the conformer was reoptimized to "Enable Point Group Symmetry" to lock the conformer in the C_i point group.

Re-optimised 1,5-hexadiene Molecule Summary with Symmetry File Type & Link .log Calculation Type FOPT Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.69254 Gradient (au) 0.00001896 Dipole Moment (Debye) 0.00 Symmetry Point Group Ci CPU Calculation Time (s) 4.0

Item Value Threshold Converged? Maximum Force 0.000060 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000316 0.001800 YES RMS Displacement 0.000099 0.001200 YES Predicted change in Energy=-1.847630D-08 Optimization completed. -- Stationary point found. As seen is the optimization summary, the Ci symmetry has been enforced, with no negligible deviation in Energy and Gradient than the previous HF/3-21G calculation.

Higher Basis Set Re-optimised 1,5-hexadiene Molecule Summary File Type & Link .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.61171 Gradient (au) 0.00000059 Dipole Moment (Debye) 0.00 Symmetry Point Group Ci CPU Calculation Time (s) 159.0

Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000008 0.000060 YES RMS Displacement 0.000003 0.000040 YES Predicted change in Energy=-1.510358D-11 Optimization completed. -- Stationary point found. The conformer was then reoptimized using the B3LYP/6-31G(d) basis set with an "ultrafine" integral grid. The relative energies of the calculations differed significantly by 2.919 au (1832 kcal mol-1), which illustrates the inaccuracy of the HF/3-21G basis set. However, the geometries of the conformer remain relatively unchanged, and is summarized below.

Comparison of Geometric Properties of Different Basis Set Calculations for 1,5-hexadiene Anti 2 Conformer

	Geometric Property	HF/3-21G	B3LYP/6-31G(d)
	Bond Length of C1-C2 & C5-C6 (Å)	1.32	1.33
	Bond Length of C2-C3 & C4-C5 (Å)	1.51	1.50
	Bond Length of C3-C4 (Å)	1.55	1.55
	Bond Angle of C1-C2-C3 & C4-C5-C6 (°)	124.8	125.3
	Bond Angle of C2-C3-C4 & C3-C4-C5 (°)	111.3	112.7

Frequency Analysis of 1,5-hexadiene Anti 2 Conformer

1,5-hexadiene Anti 2 Vibrational Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.61171 Gradient (au) 0.00000059 Dipole Moment (Debye) 0.00 Symmetry Point Group Ci CPU Calculation Time (s) 236.0

Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000010 0.001800 YES RMS Displacement 0.000005 0.001200 YES Predicted change in Energy=-1.919922D-11 Optimization completed. -- Stationary point found. The purpose of carrying out a frequency analysis is to ensure that the optimized molecule was in its energy minima, and not just in a transition state. The frequencies obtained in the calculation are the second derivative in the Potential Energy Surface graph; if the frequencies calculated are all positive in value, the molecule has been optimized to its energy minima. The frequency analysis was calculated using the same basis set and method to avoid energy discrepancies. Above, the low frequencies represent the frequencies of motion of the molecules' center of mass. Better optimizations lead to very low values of centre of mass vibrational frequencies. Thus, low frequencies within the range of ±15cm-1 are an indicator that the optimization was satisfactory, as is the case in this frequency analysis.

 Low frequencies ---   -7.6838   -2.7069   -0.0008   -0.0003   -0.0002    1.6692
 Low frequencies ---   73.5565   80.5652  121.0120

Vibrational Frequncies and IR Spectrum of 1,5-hexadiene Anti 2 Conformer

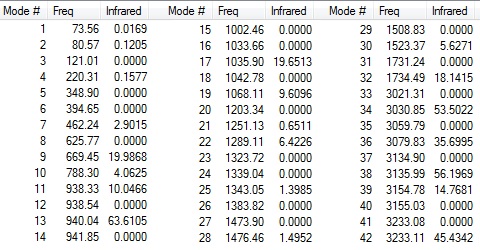
All vibrational frequencies were positive in value and "real", showing that the critical point of the optimized structure is a minima.

 Sum of electronic and zero-point Energies=           -234.469219
 Sum of electronic and thermal Energies=              -234.461869
 Sum of electronic and thermal Enthalpies=            -234.460925
 Sum of electronic and thermal Free Energies=         -234.500808

The frequency analysis was re-calculated at 0K by directly modifying the input file (found here). As shown below, the first value remains constant because the 'Sum of electronic and zero-point Energies' is calculated at 0K. At 0K, all energy values are equal because there are no additional contributions from translational, rotational and vibrational modes. Similarly, there is no additional thermal energy that contributing to the total energy of the system (H = E + RT, where T = 0, thus H=E).

 Sum of electronic and zero-point Energies=           -234.469219
 Sum of electronic and thermal Energies=              -234.469219
 Sum of electronic and thermal Enthalpies=            -234.469219
 Sum of electronic and thermal Free Energies=         -234.469219

"Chair" and "Boat" Transition Structures

In this section,a transition structure optimization was carried out by (i) computing the force constants at the beginning of the calculation, (ii) using the redundant coordinate editor, and (iii) using QST2. The objective was to visualize the reaction coordinate, run the IRC (Intrinisic Reaction Coordinate) and calculate the activation energies for the Cope rearrangement via the "chair" and "boat" transition structures.

Optimization of Allyl Fragment (CH₂CHCH₂)

Optimized Allyl Fragment (CH2CHCH2) Summary File Type & Link .log Calculation Type FOPT Calculation Method UHF Basis Set 3-21G Final Energy (au) -115.82304 Gradient (au) 0.00003119 Dipole Moment (Debye) 0.03 Symmetry Point Group C1 CPU Calculation Time (s) 38.0

Item Value Threshold Converged? Maximum Force 0.000076 0.000450 YES RMS Force 0.000025 0.000300 YES Maximum Displacement 0.000909 0.001800 YES RMS Displacement 0.000300 0.001200 YES Predicted change in Energy=-6.724446D-08 Optimization completed. -- Stationary point found. An allyl fragment was optimized with a low level basis set, and the symmetrized to obtain a fragment with C2v symmetry. This fragment is used for building the "boat" and "chair" transition structures by appending 2 of these fragments to obtain a "guess" transition state structure.

Optimizing the "Chair" Transition State (The Hessian Method)

The first method of calculation method used is known as the Hessian method. This method is the easiest, but requires the "guess" transition state to be close to the actual structure. It computes the force constant matrix in the first step of the optimisation, and then revises the "guess" structure as the optimization proceeds. Two previously optimized allyl fragments were oriented in the "chair" transition state, with the C-atom terminal ends of the allyl fragments separated by approximately 2.2 Å. The transition state was then optimized using the HF/3-21G level of theory. To do so, the 'Optimization' command was set to a 'TS (Berny)', force constants were only calculated once, and the additional keywords Opt=NoEigen were included, the latter which stops the calculation crashing if more than one imaginary frequency is detected during the optimization; which can often happen if the guess transition structure is not good enough.

Optimised Hessian Chair Transition State Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.61932 Gradient (au) 0.00003069 Dipole Moment (Debye) 0.00 Symmetry Point Group C1 CPU Calculation Time (s) 176.0

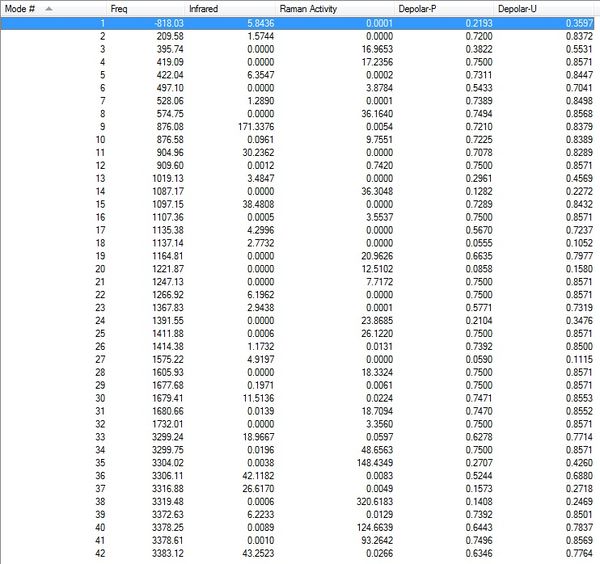
Item Value Threshold Converged? Maximum Force 0.000066 0.000450 YES RMS Force 0.000016 0.000300 YES Maximum Displacement 0.001102 0.001800 YES RMS Displacement 0.000278 0.001200 YES Predicted change in Energy=-1.352980D-07 Optimization completed. -- Stationary point found. The optimized chair transition structure possessed a C2h after the symmetrize operation, and yielded an imaginary frequency of -818cm-1 in the vibrational analysis, which correponds to the Cope rearrangement, showing that the optimization was successful. Low frequencies --- -818.0257 -1.8831 -0.0009 -0.0004 -0.0003 3.3961 Low frequencies --- 4.7588 209.5755 395.7415

 Sum of electronic and zero-point Energies=           -231.466703
 Sum of electronic and thermal Energies=              -231.461343
 Sum of electronic and thermal Enthalpies=            -231.460399
 Sum of electronic and thermal Free Energies=         -231.495209

Vibration of imaginary frequency -818 cm_-1 corresponding to the Cope rearrangement.

Optimizing the "Chair" Transition State (Reaction Coordinate Freezing)

As the Hessian method often yields misleading results, the "chair" structure was reoptimized by freezing the reaction coordinate (using Opt=ModRedundant. Once the molecule is fully relaxed, the reaction coordinate can then be unfrozen and the transition state optimization is started again. One advantage of doing this, is that it may not be necessary to compute the whole Hessian once this has been done, and just differentiating along the reaction coordinate might give a good enough guess for the initial force constant matrix. This can save a considerable amount of time in cases where the force constant calculation is expensive.

Optimised Hessian Chair Transition State Summary File Type & Link .log Calculation Type FOPT Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.61519 Gradient (au) 0.00325674 Dipole Moment (Debye) 0.00 Symmetry Point Group C1 Symmetrized Point Group C2h CPU Calculation Time (s) 35.0

Item Value Threshold Converged? Maximum Force 0.000046 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.000622 0.001800 YES RMS Displacement 0.000109 0.001200 YES Predicted change in Energy=-2.396745D-08 Optimization completed. -- Stationary point found. The two pairs of terminal carbons from the allyl fragments which form/break a bond during the Cope rearrangment were frozen at 2.2Å using the Redundant Coordinate Editor, giving a transition structure with C1 symmetry. After symmetrizing, the structure had a C2h symmetry.

Optimised Hessian Chair Transition State Summary File Type & Link .log Calculation Type FOPT Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.61932 Gradient (au) 0.00002130 Dipole Moment (Debye) 0.00 Symmetry Point Group C1 Symmetrized Point Group C2h CPU Calculation Time (s) 21.0

Item Value Threshold Converged? Maximum Force 0.000072 0.000450 YES RMS Force 0.000020 0.000300 YES Maximum Displacement 0.001608 0.001800 YES RMS Displacement 0.000407 0.001200 YES Predicted change in Energy=-1.681774D-07 Optimization completed. -- Stationary point found. The second step was to use the Hessian method on the bonds which form/break during the Cope rearrangement. This was done by using the Redundant Mod Editor to differentiate the bonds between the two termianl carbon pairs.

Chair Transition State Comparison

The geometry of the chair transition state optimized using the two methods were compared and summarized in the table below;

Comparison of Geometric Properties of Chair Transition Structures

	Geometric Property	Hessian Method	Freezing Coordinates
	Bond Length of C1-C2 & C9-C10 (Å)	1.39 (1.38934)	1.39 (1.38930)
	Bond Length of C1-C6 & C9-C14 (Å)	1.39 (1.38918)	1.39 (1.38929)
	Bond Length of C2-C10 (Å)	2.21 (2.2084)	2.21 (2.2072)
	Bond Length of C6-C14 (Å)	2.21 (2.2094)	2.21 (2.2074)

Considering that the Final Energies calculated from the Hessian method and the Freezing method were similiar (-231.61932 a.u.), and that the geometric properties of the Chair transition state in both calculations were very similiar (Bond lengths are usually calculated to 2 decimal places), it is concluded that the optimization were both successful, and that the "guess" transition state was close to the actual chair transition state.

"Boat" Transition State Optimization using QS2 Method

A "boat" transition structure was optimized using the QST2 method. To do so, the reactants and products for a reaction need to be specified so that the calculation interpolates between the two structures to find the transition state located between them. The optimized 1,5-hexadiene Anti 2 conformer was duplicated as the reactant and product molecule. It is then oriented and renumbered as so that both the reactant and the product were numbered in the same way, as shown below.

Reactant	Product

Optimized Boat Transition Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.61932 Gradient (au) 0.00004773 Dipole Moment (Debye) 0.00 Symmetry Point Group C2H CPU Calculation Time (s) 7.0

Item Value Threshold Converged? Maximum Force 0.000037 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.000705 0.001800 YES RMS Displacement 0.000265 0.001200 YES Predicted change in Energy=-2.465559D-07 Optimization completed. -- Stationary point found. Low frequencies --- -818.0098 -0.0020 -0.0011 0.0007 3.0643 5.0143 Low frequencies --- 5.1439 209.6603 396.1197 The optimized structure resembles a chair transition structure but more dissociated, which was not the expected boat transition structure. This is due to the fact when the calculation linearly interpolated between the two structures, it simply translated the top allyl fragment and did not even consider the possibility of a rotation around the central bonds. It is clear that the QST2 method is never going to locate the boat transition structure if starting from the reactant and product structures above.

To correct for this, the reactant and product geometries were modified to look closer to the boat transition structure. The central C-C-C-C dihedral angle was set to 0° and the inside C-C-C angle was set to 100°.

Reoptimized Boat Transition Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.60280 Gradient (au) 0.00004114 Dipole Moment (Debye) 0.16 Symmetry Point Group CS CPU Calculation Time (s) 6.0

Vibration corresponding to -840cm-1 Item Value Threshold Converged? Maximum Force 0.000094 0.000450 YES RMS Force 0.000024 0.000300 YES Maximum Displacement 0.001191 0.001800 YES RMS Displacement 0.000390 0.001200 YES Predicted change in Energy=-2.584619D-07 Optimization completed. -- Stationary point found. Low frequencies --- -840.2217 -1.5560 -0.0012 -0.0009 0.0017 4.2566 Low frequencies --- 7.8246 155.3803 382.0866 The optimized structure is the expected boat structure in this calculation, with an imaginary low frequency at -340cm-1 corresponding to the Cope Rearrangment bond breaking-forming.

"Boat" Transition State Optimization using QS3 Method

Although the QST2 method, has the advantage of being fully automated, it often fails if the reactants or products are not close to the transition structure. The QST3 method however, which allows an input of the geometry of a guess transition structure, which can been used for the calculations. The guess "Boat" transition structure was built and renumbered so that its numbering would match the ones of the reactant and product, and a QST3 calculation performed.

Reactant	Transition State	Product

Optimized QTS3 Boat Transition Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.60280 Gradient (au) 0.00000618 Dipole Moment (Debye) 0.16 Symmetry Point Group CS CPU Calculation Time (s) 7.0

Item Value Threshold Converged? Maximum Force 0.000022 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000563 0.001800 YES RMS Displacement 0.000106 0.001200 YES Predicted change in Energy=-1.646979D-08 Optimization completed. -- Stationary point found. Low frequencies --- -840.0535 -2.5892 -1.0382 -0.0013 -0.0003 0.0047 Low frequencies --- 1.9320 155.2387 382.0876 The QTS3 optimized structure resembles the structure calculated using the QTS2 method, as shown in the Jmol structure, the summary and log file, and the frequency of the imaginary vibration at -840cm-1, showing that the optimization was succesful.

 Sum of electronic and zero-point Energies=           -231.450927
 Sum of electronic and thermal Energies=              -231.445299
 Sum of electronic and thermal Enthalpies=            -231.444354
 Sum of electronic and thermal Free Energies=         -231.479773

Boat Transition Structure Comparison

Comparison of Geometric Properties of Boat Transition Structures

Geometric Property	QTS2	QTS3
Bond Length of C1-C2 & C5-C6 (Å)	1.38 (1.38152)	1.38 (1.38144)
Bond Length of C2-C3 & C4-C5 (Å)	1.38 (1.38150)	1.38 (1.38147)
Bond Length of C1-C6 (Å)	2.14 (2.13989)	2.14 (2.13981)
Bond Length of C3-C4 (Å)	2.14 (2.13995)	2.14 (2.13977)

Both the boat transition structures have the correct atom numbering. Also the geometric properties of the transition structures of the QTS2 and QTS3 methods of calculation are very similiar, showing that the boat transition structures calculated are consistent.

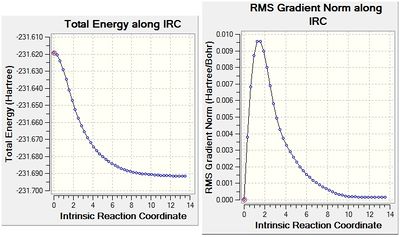
Intrinsic Reaction Coordinates (IRC)

The IRC method can be used to predict from which conformer of 1,5-hexadiene originates from the chair transition structure. It follows the minimum energy path from a transition structure, by taking small geometry steps in the direction where the slope of the potential energy surface is steepest, until it reaches a local minimum. The "Freeze" method calculation of the chair transition state was used for the IRC calculation.

Chair Transition Structure IRC Summary (50 Steps) File Type & Link .log Calculation Type IRC Final Energy (au) -231.69158 Gradient (au) 0.00015225 Dipole Moment (Debye) 0.36 Symmetry Point Group C2 CPU Calculation Time (s) 885.4

As the chair transition state was symmetrical, the IRC calculation was set to "forward only". A total of 50 points were specified along the IRC, which lead to a calculation which determined that the minima was at set (44), which is shown in the Jmol file.

Chair Transition Structure IRC Summary (60 Steps) File Type & Link .log Calculation Type IRC Final Energy (au) -231.69158 Gradient (au) 0.00015225 Dipole Moment (Debye) 0.36 Symmetry Point Group C2 CPU Calculation Time (s) 891.6

The IRC was recalculated, with 60 sets on the IRC to ensure that the minima was met in the first IRC. The minma was also at set (44), which was the same structure as previously calculated, indicating that the minimum at the IRC has been reached.

The last point on the IRC (Set 44), is then optimized to a minimum at a HF/3-21G level of theory with vibrational analysis to ensure that the structure was at its minimum in the Potential Energy Surface.

Optimized Set 44 Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.69167 Gradient (au) 0.00000475 Dipole Moment (Debye) 0.38 Symmetry Point Group C2 CPU Calculation Time (s) 7.0

Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000167 0.001800 YES RMS Displacement 0.000049 0.001200 YES Predicted change in Energy=-2.173227D-09 Optimization completed. -- Stationary point found. Low frequencies --- -1.3078 -0.8712 -0.0073 0.0041 0.0053 1.4009 Low frequencies --- 63.6549 98.2277 113.3916 The optimized structure is identified as the Gauche 2 conformer of 1,5-hexadiene, as found in this table. It is similiar in Energy, point group, and geometry. Thus, it can be concluded that through the IRC method, the conformer that leads to the chair transition state structure in the Cope Rearrangement of 1,5-hexadiene was found to be the Gauche 2 conformer.

 Sum of electronic and zero-point Energies=           -231.538704
 Sum of electronic and thermal Energies=              -231.531794
 Sum of electronic and thermal Enthalpies=            -231.530850
 Sum of electronic and thermal Free Energies=         -231.569476

Activation Energy

The last step is to calculate the activation energies for the reaction via both transition structures. To do this, the chair and boat transition structures were reoptimized using the B3LYP/6-31G* level of theory from the HF/3-21G optimized structures and frequency calculations were performed. Once the calculations have converged, both the geometries and the difference in energies between the reactants and transition states at the two levels of theory were compared. The geometries are reasonably similar, but the energy differences are markedly different. This shows that it is more computationally efficient to map the potential energy surface using the low level of theory first and then to reoptimize at the higher level.

Reoptimized Chair Transition Structure

Reoptimized Chair Transition Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.55693 Gradient (au) 0.00000108 Dipole Moment (Debye) 0.00 Symmetry Point Group C2H CPU Calculation Time (s) 81.0

Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000031 0.000060 YES RMS Displacement 0.000009 0.000040 YES Predicted change in Energy=-1.492370D-10 Optimization completed. -- Stationary point found. Low frequencies --- -569.3626 0.0005 0.0010 0.0012 4.9991 11.1492 Low frequencies --- 13.3587 195.9150 262.5148 Sum of electronic and zero-point Energies= -234.414909 Sum of electronic and thermal Energies= -234.408980 Sum of electronic and thermal Enthalpies= -234.408036 Sum of electronic and thermal Free Energies= -234.443148

Reoptimized Boat Transition Structure

Reoptimized Boat Transition Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.54308 Gradient (au) 0.00000059 Dipole Moment (Debye) 0.06 Symmetry Point Group C2V CPU Calculation Time (s) 137.0

Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000027 0.000060 YES RMS Displacement 0.000006 0.000040 YES Predicted change in Energy=-6.032194D-11 Optimization completed. -- Stationary point found. Low frequencies --- -532.1378 -11.2601 0.0002 0.0008 0.0008 1.9317 Low frequencies --- 6.8664 133.8462 259.9736 Sum of electronic and zero-point Energies= -234.402356 Sum of electronic and thermal Energies= -234.396012 Sum of electronic and thermal Enthalpies= -234.395068 Sum of electronic and thermal Free Energies= -234.431126

Geometry Comparison of Transition States at Two Levels of Theory

The geometries of the chair and boat transition states calculated using the HF/3-21G and B3LYP/6-31G* levels of theory were compared and summarized in the table below.

Comparison of Geometric Properties of Transition Structures at Two Levels of Theory

Structure	Chair Transition State			Boat Transition State
Level of Theory	HF/3-21G	B3LYP/6-31G*	Literature	HF/3-21G	B3LYP/6-31G*	Literature
Bond Length of C1-C2, C5-C6, C2-C3 & C4-C5(Å)	1.39	1.41	1.401	1.38	1.39	1.390
Bond Length of C1-C6 & C3-C4 (Å)	2.21	1.97	2.086	2.14	2.21	2.208

The geometries of the calculated transition states at different levels of theory were relatively similiar, but it was found that the the geometry of the transition state calculates using the B3LYP/6-31G* level of theory was more similiar to literature values than the lower level HF/3-21G, as expected.

Energy Comparison of Transition States

The activation energies at 0 K can be calculated from difference between the 'sum of electronic and zero-point energies' of the reactant and the transition states, while the activation energies at 298.15K can be calculated from the difference between 'Sum of electronic and thermal energies' of the reactant and transition states, which are properties that are found in the "Thermochemistry" section in the respective .log files. The calculation can be found here.

Summary of energies (Hartree/a.u.)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.466703	-231.461343	-234.55693	-234.414909	-234.408980
Boat TS	-231.60280	-231.450927	-231.445299	-234.54308	-234.402356	-234.396012
Reactant (anti2)	-231.69167	-231.538704	-231.531794	-234.61171	-234.469219	-234.461869

*1 Hartree/a.u. = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	34.08	33.19	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.33	44.7 ± 2.0

As expected, the higher level of theory of the 6-31G(d)basis set provides results which are closer to experimental values.

The chair transition state is lower in energy than the boat transition state, and hence, leads to a smaller activation energy, which suggests that the chair geometry is the preferred transition state of the Cope rearrangement. This behavior mimics the geometric properties of cyclohexane, which also favours the chair geometry conformer, as all the atoms in a chair conformer are in a staggered conformation, while the boat geometry forces two pairs of carbon atoms to be parallel and in an eclipsed conformation.

As can be seen from the table, the activation energy for a 1,5-hexadiene Anti 2 conformer to a Chair transition state at 0K (34.08kcal/mol) is quite similiar to the experimental activation energy for a Cope Rearrangement cia the Chair Transition structure at 0K (33.5 ± 0.5kcal/mol). However, based on the previous IRC calculations (here), the conformer of 1,5-hexadiene to originate from the chair transittion structure was found to be Gauche 2 instead. To further investigate this, the Gauche 2 conformer was reoptimized at a B3LYP/6-31G* level of theory, and the activation energy calculated.

Reoptimized 1,5-hexadiene Gauche 2 Conformer File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.61070 Gradient (au) 0.00000009 Dipole Moment (Debye) 0.44 Symmetry Point Group C2 CPU Calculation Time (s) 198.0

Item Value Threshold Converged? Maximum Force 0.000000 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000009 0.000060 YES RMS Displacement 0.000003 0.000040 YES Predicted change in Energy=-1.277752D-12 Optimization completed. -- Stationary point found. Low frequencies --- -2.8377 -0.0009 -0.0006 -0.0005 3.9448 5.0754 Low frequencies --- 65.6748 101.7135 108.1470 Sum of electronic and zero-point Energies= -234.468244 Sum of electronic and thermal Energies= -234.460957 Sum of electronic and thermal Enthalpies= -234.460013 Sum of electronic and thermal Free Energies= -234.499225

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932	-231.466703	-231.461343	-234.55693	-234.414909	-234.408980
Reactant (Gauche2)	-231.69254	-231.539539	-231.532566	-234.61070275	-234.468244	-234.460957

*1 Hartree/a.u. = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.69	33.47	32.62	33.5 ± 0.5

At 0k and B3LYP/6-31G* level of theory, the calculated activation energy for a 1,5-hexadiene Gauche 2 conformer transitioning into the Chair transition state is 33.47kcal/mol, which is even closer to experimental values of 33.5 ± 0.5kcal/mol than the Anti 2 conformer. This information highly supports the theory that in the Cope Rearrangement of 1,5-hexadiene, the preferred reaction mechanism is via the Gauche 2 conformer and the Chair Transition State. The calculation can be found here.

Conclusion

From Gaussian calculations at a B3LYP/6-31G* level of theory, it was concluded that the preferred reaction mechanism for the Cope Rearrangement is a Gauche 2 conformer as the reactant and via a Chair Transition State. At 0k, the activation energy for this transition was found to be 33.47 kcal/mol, while at 298.15K, the activation energy was found to be 32.62kcal/mol.

Gauche 2 Conformer

Chair Transition State

Gauche 2 Conformer

The Dies Alder Cycloaddition

Diels Alder cycloaddition

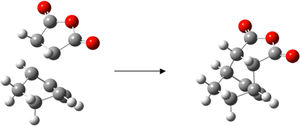
The Diels Alder reaction belongs to a class of reactions known as pericyclic reactions. The π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene. Whether or not the reactions occur in a concerted stereospecific fashion (allowed) or not (forbidden) depends on the number of π electrons involved. In general the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. The nodal properties allow one to make predictions according to the following rule:

If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed.

The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden.

If the dieneophile is substituted, with substituents that have π orbitals that can interact with the new double bond that is being formed in the product, then this interaction can stabilise the regiochemistry (i.e. head to tail versus tail to head) of the reaction. In this computational exercise, the nature of the transition structure for the Diels Alder reaction was studied, both for the prototypical reaction and for the case where both diene and dieneophile carry substituents, and where secondary orbital effects are possible. Since the factors that control the nature of the transition state are quantum mechanical in origin, methods based upon quantum chemistry shall be used for this computation.

The Dies Alder reaction that will be used for this computational experiment will be a Dies Alder [_π4_s +_π2_s] cycloaddition between s-cis-1,3-butadiene and ethylene.

Dies Alder [_π4_s +_π2_s] cycloaddition

Optimization of Ethylene

Molecule was optimized to a near zero gradient, Force Constants and Displacements were converged, and the vibrational analysis indicates a minima in the PES, as the low frequency vibrations were ±15cm_-1. Optimization was successful.

Optimized Ethylene Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -78.58745869 Gradient (au) 0.00000484 Dipole Moment (Debye) 0.00 Symmetry Point Group D2H CPU Calculation Time (s) 7.0

Item Value Threshold Converged? Maximum Force 0.000010 0.000015 YES RMS Force 0.000006 0.000010 YES Maximum Displacement 0.000027 0.000060 YES RMS Displacement 0.000016 0.000040 YES Predicted change in Energy=-6.205088D-10 Optimization completed. -- Stationary point found. Low frequencies --- -4.7728 -3.4085 -0.0010 -0.0007 -0.0004 2.6265 Low frequencies --- 834.7584 956.0916 976.0679 Sum of electronic and zero-point Energies= -78.536235 Sum of electronic and thermal Energies= -78.533193 Sum of electronic and thermal Enthalpies= -78.532249 Sum of electronic and thermal Free Energies= -78.557110

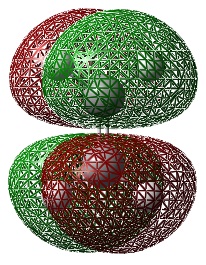
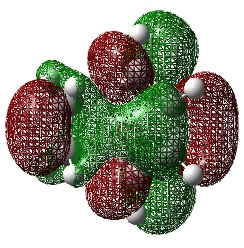
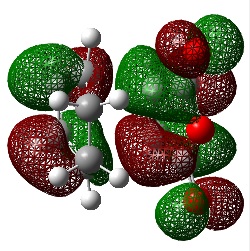
Ethylene Frontier Orbitals

An Energy calculation was performed on the ethylene structure at the B3LYP/6-31G* level of theory. The HOMO and LUMO of the structure were visualized using the checkpoint file.

Ethylene MO Summary File Type & Link .chk Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -78.58745830 Dipole Moment (Debye) 0.00 Symmetry Point Group D2H CPU Calculation Time (s) 5.0

Molecular Orbital HOMO LUMO Structure Energy Level E=-0.26663 E=+0.01879 Symmetry with respect to plane Symmetric Antisymmetric

Optimization of s-cis-1,3-butadiene

s-cis-1,3-butadiene was optimized using the AM1 semi-empirical molecular orbital method and then reoptimized using the higher levels of theory HF/3-21G and B3LYP/6-31G(*). Each optimization was successfully converged and followed by a vibrational analysis to ensure a minimum in the Potential Energy Surface.

Optimized cis-1,3-butadiene Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RAM1 Basis Set ZDO Final Energy (au) 0.04879720 Gradient (au) 0.00001727 Dipole Moment (Debye) 0.04 Symmetry Point Group C2V CPU Calculation Time (s) 2.0

Item Value Threshold Converged? Maximum Force 0.000061 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.000438 0.001800 YES RMS Displacement 0.000150 0.001200 YES Predicted change in Energy=-2.813141D-08 Optimization completed. -- Stationary point found. Low frequencies --- -37.2602 -0.0325 -0.0288 -0.0005 5.9181 6.7453 Low frequencies --- 9.3796 312.6721 485.4793 Sum of electronic and zero-point Energies= 0.134552 Sum of electronic and thermal Energies= 0.138572 Sum of electronic and thermal Enthalpies= 0.139516 Sum of electronic and thermal Free Energies= 0.109172

Optimized cis-1,3-butadiene Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -154.05394305 Gradient (au) 0.00011873 Dipole Moment (Debye) 0.03 Symmetry Point Group C2V CPU Calculation Time (s) 4.0

Item Value Threshold Converged? Maximum Force 0.000239 0.000450 YES RMS Force 0.000078 0.000300 YES Maximum Displacement 0.000740 0.001800 YES RMS Displacement 0.000291 0.001200 YES Predicted change in Energy=-2.461500D-07 Optimization completed. -- Stationary point found. Low frequencies --- -150.9367 -0.0012 -0.0011 -0.0007 8.4685 11.0084 Low frequencies --- 17.6002 335.4976 573.4751 Sum of electronic and zero-point Energies= -153.962200 Sum of electronic and thermal Energies= -153.958418 Sum of electronic and thermal Enthalpies= -153.957474 Sum of electronic and thermal Free Energies= -153.987467

Optimized cis-1,3-butadiene Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -155.98595131 Gradient (au) 0.00000067 Dipole Moment (Debye) 0.09 Symmetry Point Group C2V CPU Calculation Time (s) 37.0

Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000005 0.000060 YES RMS Displacement 0.000002 0.000040 YES Predicted change in Energy=-1.255951D-11 Optimization completed. -- Stationary point found. Low frequencies --- -125.3437 -6.0025 -2.3069 -0.0016 -0.0012 -0.0010 Low frequencies --- 2.8480 295.3468 518.2367 Sum of electronic and zero-point Energies= -155.900839 Sum of electronic and thermal Energies= -155.896796 Sum of electronic and thermal Enthalpies= -155.895852 Sum of electronic and thermal Free Energies= -155.926257

An imaginary frequency was found in the vibrational anaylsis (-125 cm-1 at the B3LYP/6-31G(*) level of theory). Upon , inpection, the vibration corresponding to this frequency corresponds to an assymetrical bending in/out of the plane. This suggests that the planar cis-butadiene structure is not at an energy minima, and other conformers which are not planar, are at the energy minima.

Imaginary Vibration at -125 cm-1

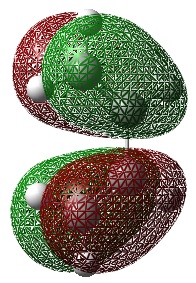
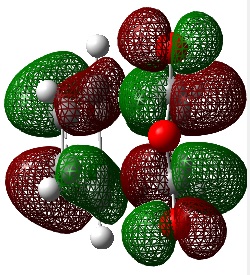
cis-Butadiene Frontier Orbitals

An Energy calculation was performed on the cis butadiene structure at the B3LYP/6-31G* level of theory. The HOMO and LUMO of the structure were visualized using the checkpoint file.

cis-Butadiene MO Summary File Type & Link .chk Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -155.98595131 Gradient (au) 0.000000007 Dipole Moment (Debye) 0.0853 Symmetry Point Group C2V CPU Calculation Time (s) 5.0

Molecular Orbital HOMO LUMO Structure Energy Level E=-0.22733 E=-0.03014 Symmetry with respect to plane Antisymmetric Symmetric

Optimization of Cyclohexene

Cyclohexene was optimized using the levels of theory HF/3-21G and B3LYP/6-31G(*). Each optimization was successfully converged and followed by a vibrational analysis to ensure a minimum in the Potential Energy Surface.

Optimized Cyclohexene Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.71058873 Gradient (au) 0.00003106 Dipole Moment (Debye) 0.28 Symmetry Point Group C2V CPU Calculation Time (s) 6.0

Item Value Threshold Converged? Maximum Force 0.000108 0.000450 YES RMS Force 0.000025 0.000300 YES Maximum Displacement 0.000572 0.001800 YES RMS Displacement 0.000186 0.001200 YES Predicted change in Energy=-1.347426D-07 Optimization completed. -- Stationary point found. Low frequencies --- -273.9773 -150.7668 -5.3442 -0.0030 0.0002 0.0005 Low frequencies --- 5.6203 5.8847 397.8178 Sum of electronic and zero-point Energies= -231.553338 Sum of electronic and thermal Energies= -231.549208 Sum of electronic and thermal Enthalpies= -231.548264 Sum of electronic and thermal Free Energies= -231.580420

Optimized Cyclohexene Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.63289900 Gradient (au) 0.00000183 Dipole Moment (Debye) 0.3496 Symmetry Point Group C2V CPU Calculation Time (s) 139.0

Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000016 0.000060 YES RMS Displacement 0.000006 0.000040 YES Predicted change in Energy=-1.800511D-10 Optimization completed. -- Stationary point found. Low frequencies --- -262.8960 -133.2036 -8.8995 -0.0008 -0.0006 0.0002 Low frequencies --- 3.2331 3.3492 361.9719 Sum of electronic and zero-point Energies= -234.486224 Sum of electronic and thermal Energies= -234.481818 Sum of electronic and thermal Enthalpies= -234.480874 Sum of electronic and thermal Free Energies= -234.513422

Two imaginary frequencies were found at -263 cm^-1 and -133 cm^-1. These frequencies correspond to the half chair conformation (-263 cm^-1, and half boat conformation (-133 cm^-1) of cyclohexane, which shows that the optimized structure was not at the energy minima. These conformations are the most stable conformers for cyclohexene,and the half chair the more stable conformer, thus the corresponding vibration is of larger magnitude. However, since the pericyclic reaction in question is assumed to proceed in a concerted, synchronous fashion, , we will assume that the product cyclohexene of the Dies Alder Reaction is the half boat conformer, not the half chair transition state.

Imaginary Vibration Corresponding to -263 cm-1

Imaginary Vibration Corresponding to -133 cm-1

Optimization of the Dies Alder Transition State

To find the transition state of the Dies Alder reaction between cis-butadiene and ethylene, a "Freezing Coordinates" and QTS3 method will be employed. This method calculates the transition state based on a reactant, a product, and a "guess" transition state structure. For this reaction, we have calculated that the planar cis-butadiene and the planar cyclohexene are the energy minima structures based on frequency calculations. However, for the QTS3 calculations, the "reactants" and "products" need not be optimized minima structures. Therefore, for the purpose of finding the transition state, the planar molecules will be used.

Optimizing Transition State by Freezing Coordinates

The previously optimised planar cis-butadiene and ethylene fragments were oriented such that they would resemble the halfboat cyclohexene structure optimized previously, and freezing the separation of the terminal ends by approximately 2.2 Å. The transition state was then optimized using the HF/3-21G level of theory.

Optimized Transition State Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RHF Basis Set 3-21G Final Energy (au) -231.60320843 Gradient (au) 0.00015087 Dipole Moment (Debye) 0.5750 Symmetry Point Group C1 CPU Calculation Time (s) 7.0

Item Value Threshold Converged? Maximum Force 0.000133 0.000450 YES RMS Force 0.000027 0.000300 YES Maximum Displacement 0.001478 0.001800 YES RMS Displacement 0.000292 0.001200 YES Predicted change in Energy=-1.829348D-07 Optimization completed. -- Stationary point found. Low frequencies --- -816.6902 -0.0002 0.0007 0.0009 2.4027 5.1439 Low frequencies --- 8.0606 166.7360 284.0357 Sum of electronic and zero-point Energies= -231.451348 Sum of electronic and thermal Energies= -231.445659 Sum of electronic and thermal Enthalpies= -231.444714 Sum of electronic and thermal Free Energies= -231.480290

The guess transition structure is then reoptimized at the RHF/6-31G(*) level using a Hessian method

Optimized Transition State Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method B3LYP Basis Set 6-31G(d) Final Energy (au) -232.87960559 Gradient (au) 0.00000622 Dipole Moment (Debye) 0.5064 Symmetry Point Group C1 CPU Calculation Time (s) 94.7

Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000241 0.001800 YES RMS Displacement 0.000061 0.001200 YES Predicted change in Energy=-4.470580D-10 Optimization completed. -- Stationary point found. Low frequencies --- -902.6197 -2.2891 -2.1349 -0.0009 -0.0006 0.0008 Low frequencies --- 1.5128 161.5976 262.5019 Sum of electronic and zero-point Energies= -232.728939 Sum of electronic and thermal Energies= -232.723105 Sum of electronic and thermal Enthalpies= -232.722161 Sum of electronic and thermal Free Energies= -232.757991

Optimizing Transition State by QST3 Method

The previously optimised and oriented planar cis-butadiene and ethylene fragments were input as reactants while the half boat structure was input as the product. The previous structure from the Freezing Method calculation was input as the "guess" transition structure. A QST3 calculation was then performed at the B3LYP/6-31G(*) level of theory.

Optimized Transition State Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.54389653 Gradient (au) 0.00001764 Dipole Moment (Debye) 0.3947 Symmetry Point Group C1 CPU Calculation Time (s) 339.7

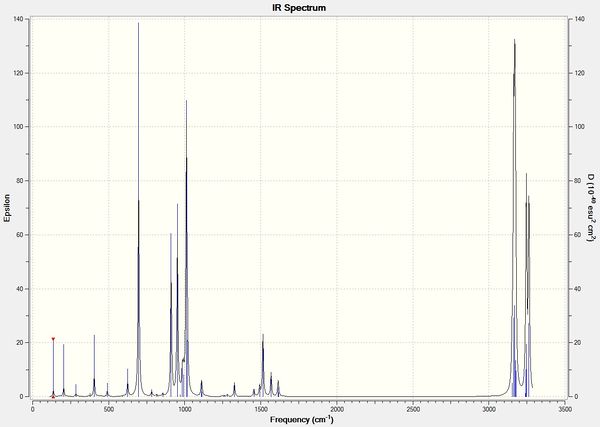
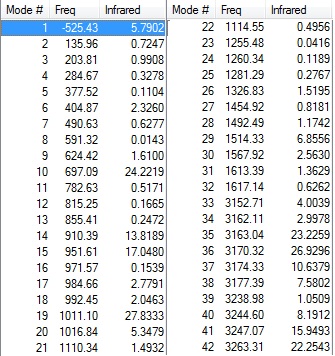
Item Value Threshold Converged? Maximum Force 0.000023 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.001249 0.001800 YES RMS Displacement 0.000389 0.001200 YES Predicted change in Energy=-2.857020D-08 Optimization completed. -- Stationary point found. Low frequencies --- -525.4316 -4.9436 -0.0006 -0.0003 0.0003 11.1457 Low frequencies --- 20.1646 136.0151 203.8233 Sum of electronic and zero-point Energies= -234.403322 Sum of electronic and thermal Energies= -234.396906 Sum of electronic and thermal Enthalpies= -234.395962 Sum of electronic and thermal Free Energies= -234.432887

Geometric Properties of the Transition State

Bond Lengths in the Reactants and Transition State

Structure	Bonds	Reactants	Transition State
	C1-C2	1.33 (1.33094)	1.39 (1.38604)
	C4-C5	1.47 (1.47139)	1.41 (1.40717)
	C3-C4/C5-C6	1.34 (1.33992)	1.38 (1.38312)
	C2-C3/C1-C6	-	2.27 (2.27190)

Typical sp3 C-C bond lengths are 1.54 Å, while typical sp2 C=C bond lengths are 1.32 Å, while the Van Der Wall radius of the carbon atom is 1.7 Å. The bondlength of the partly formed σ C-C bonds in the Transition Structure (2.27 Å), is more than the typical C-C bond length, but less than twice the Van Der Wall radii of carbon atoms. This suggests that there is an overlap of the Van Der Waals radii between the two terminal carbon atoms, leading to the partially formed σ bonds. As seen from the transition structure, these partially formed bonds are of equal length, furher proof that this Dies Alder Reaction is a concerted, synchronous reaction.

Furthermore, we observe that the C=C double bonds in both ethylene and cis butadiene becomes shorter in the transition state, while the C-C bond becomes longer in the transition state. This results in all C-C bonds in the transition structure to be of comparable lengths. This illustrates a delocalisation of electrons in the transition state not unlike those in aromatic structures like benzene, thus showing that the reaction proceeds in a cyclic manner.

Vibrational Analysis of Transition State

The imaginary vibration at -525 cm-1 corresponds to the Diels-Alder reaction. As shown, the bond forming/breaking occurs in a concerted, synchronous fashion. This contrasts with the lowest positive frequency, occurring at 136 cm-1, in which both fragments clearly show separate motions, and is assynchronous.

Imaginary vibration corresponding to -525 cm-1

Vibration corresponding to 136 cm-1

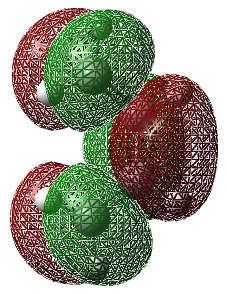
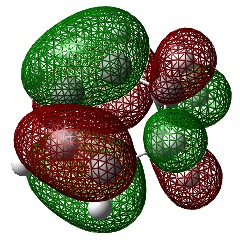
HOMO and LUMO Comparison

An Energy calculation was performed on the optimized transition state structure obtained from the QST3 method. cis-Butadiene MO Summary File Type & Link .chk Calculation Type SP Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -234.54389653 Dipole Moment (Debye) 0.3947 Symmetry Point Group C1 CPU Calculation Time (s) 339.7 Ethylene cis-Butadiene Transition State LUMO E= +0.01879 Antisymmetric E= -0.03014 Symmetric E= -0.0858 Symmetric HOMO E= -0.26663 Symmetric E= -0.22733 Antisymmetric E= -0.21894 Symmetric 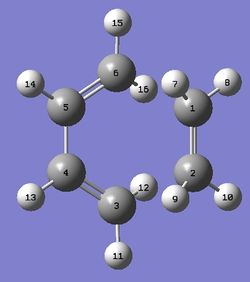This Dies Alder reaction is a [4+2] pericyclic reaction, with the butadiene molecule contributing 4 electrons and the ethylene molecule contributing 2 electrons. Again, pericyclic reactions are subject to the following rules; If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed. The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden. Both the HOMO and LUMO of the transition state are symmetrical to the plane of symmetry bisecting the structures. Thus, the orbitals that were used to form these MOs have to be symmetrical to the plane of symmetry too. The only HOMO/LUMO pair that have are symmetrical is the HOMO of ethylene and LUMO of cis-butadiene, which are the MO's giving rise to the the HOMO and LUMO of the transition state. Regioselectivity of the Diels Alder Reaction The objective of this section of the experiment is to study the regioselectivity of the Dies Alder Reaction, in particular, the reaction between cycloheca-1,3-diene and maleic anhydride. Cyclohexa-1,3-diene undergoes facile reaction with maleic anhydrideto give primarily the endo adduct. The reaction is supposed to be kinetically controlled so that the exo transition state should be higher in energy. This reaction is illustrated below. 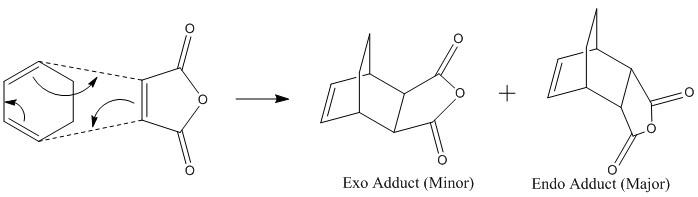Optimization of Reactants and Products Optimization of Cyclohexa-1,3-diene Optimised Cyclohexa-1,3-diene Molecule Summary File Type & Link .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -233.41588448 Gradient (au) 0.00011248 Dipole Moment (Debye) 0.5483 Symmetry Point Group C2V CPU Calculation Time (s) 26.0 Item Value Threshold Converged? Maximum Force 0.000356 0.000450 YES RMS Force 0.000055 0.000300 YES Maximum Displacement 0.001030 0.001800 YES RMS Displacement 0.000254 0.001200 YES Predicted change in Energy=-3.856836D-07 Optimization completed. -- Stationary point found. Optimization of Maleic Anhydride Optimised Maleic Anhydride Molecule Summary File Type & Link .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -379.28954459 Gradient (au) 0.00004134 Dipole Moment (Debye) 4.0719 Symmetry Point Group C2V CPU Calculation Time (s) 20.0 Item Value Threshold Converged? Maximum Force 0.000102 0.000450 YES RMS Force 0.000036 0.000300 YES Maximum Displacement 0.000442 0.001800 YES RMS Displacement 0.000160 0.001200 YES Predicted change in Energy=-8.062601D-08 Optimization completed. -- Stationary point found. Optimization of Exo Adduct Optimised Exo Adduct Molecule Summary File Type & Link .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -612.75578539 Gradient (au) 0.00003177 Dipole Moment (Debye) 4.7600 Symmetry Point Group CS CPU Calculation Time (s) 86.0 Item Value Threshold Converged? Maximum Force 0.000055 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.001663 0.001800 YES RMS Displacement 0.000286 0.001200 YES Predicted change in Energy=-1.731421D-07 Optimization completed. -- Stationary point found. Optimization of Endo Adduct Optimised Endo Adduct Molecule Summary File Type & Link .log Calculation Type FOPT Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -612.75828959 Gradient (au) 0.00006979 Dipole Moment (Debye) 5.0199 Symmetry Point Group CS CPU Calculation Time (s) 88.0 Item Value Threshold Converged? Maximum Force 0.000098 0.000450 YES RMS Force 0.000026 0.000300 YES Maximum Displacement 0.001696 0.001800 YES RMS Displacement 0.000359 0.001200 YES Predicted change in Energy=-4.522956D-07 Optimization completed. -- Stationary point found. Optimization of the Transition States Both Transition states were optimized using the QST3 method using the B3LYP/6-31G* level of theory. Guess exo and endo transition structures were built, and the reactants, (Cyclohexa-1,3-diene and Maleic Anhydride) were oriented in such a way which favours the guess transition structures. Optimization of the Exo Transition State Optimized Transition State Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -612.67931096 Gradient (au) 0.00000287 Dipole Moment (Debye) 5.5501 Symmetry Point Group C1 CPU Calculation Time (s) 496.0 Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000486 0.001800 YES RMS Displacement 0.000121 0.001200 YES Predicted change in Energy=-3.899144D-09 Optimization completed. -- Stationary point found. Low frequencies --- -448.4962 -13.9293 -11.7622 0.0010 0.0013 0.0014 Low frequencies --- 3.0597 53.3060 109.0928 Sum of electronic and zero-point Energies= -612.498013 Sum of electronic and thermal Energies= -612.487662 Sum of electronic and thermal Enthalpies= -612.486717 Sum of electronic and thermal Free Energies= -612.534265 An imaginary vibration at -448 cm-1 corresponding to the concerted, synchronous mechanism of the Dies Alder Reaction was found. Imaginary vibration at 448 cm-1 Optimization of the Endo Transition State Optimized Transition State Structure Summary File Type & Link .log Calculation Type FREQ Calculation Method RB3LYP Basis Set 6-31G(d) Final Energy (au) -612.68339638 Gradient (au) 0.00003786 Dipole Moment (Debye) 6.1141 Symmetry Point Group C1 CPU Calculation Time (s) 488.0 Item Value Threshold Converged? Maximum Force 0.000091 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.001785 0.001800 YES RMS Displacement 0.000487 0.001200 YES Predicted change in Energy=-1.550842D-07 Optimization completed. -- Stationary point found. Low frequencies --- -447.5171 -14.5044 0.0009 0.0012 0.0012 3.8640 Low frequencies --- 11.1505 59.5742 118.3854 Sum of electronic and zero-point Energies= -612.502136 Sum of electronic and thermal Energies= -612.491783 Sum of electronic and thermal Enthalpies= -612.490839 Sum of electronic and thermal Free Energies= -612.538324 An imaginary vibration at -448 cm-1 corresponding to the concerted, synchronous mechanism of the Dies Alder Reaction was found. Imaginary vibration at 448 cm-1 Comparison of Energies Exo Transition State Endo Transition State Sum of electronic Energies = -612.67931096 Sum of electronic and zero-point Energies= -612.498013 Sum of electronic and thermal Energies= -612.487662 Sum of electronic and thermal Enthalpies= -612.486717 Sum of electronic and thermal Free Energies= -612.534265 Sum of electronic Energies = -612.68339638 Sum of electronic and zero-point Energies= -612.502136 Sum of electronic and thermal Energies= -612.491783 Sum of electronic and thermal Enthalpies= -612.490839 Sum of electronic and thermal Free Energies= -612.538324 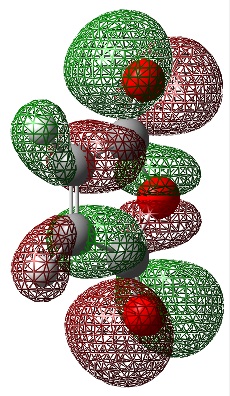As seen from the table, the endo transition state is lower in energy than the exo transition structure. This leads to a lower activation energy for the reactants to transition into the endo Transition State. Thus, the calculation proves that the Endo product of the Dies Alder reaction would be the major product in the Dies Alder reaction. The reasons for this difference in energy is explained in the sections below. Comparison of Transition State Geometries Comparison of Bond Lengths (Å) of Transition Structures and Reactants Bond(s) Exo Transition State Endo Transition State C1-C2 1.40 (1.39790) 1.39 (1.39394) 1.34 (1.33565) C10-C15/C13-C14 1.39(1.39140/1.39142) 1.39 (1.39135/1.39110) 1.34 (1.33962) C14-C15 1.40(1.40345) 1.40 (1.40309) 1.47 (1.46726) C1-C10/C2-C13 2.29(2.29068/2.29046) 2.27(2.26513/2.27033) - As shown on the table, bonds which are initially double bonds in the reactant (C1-C2 and C10-C15/C13-C14) become longer in the transition states while bonds which are initially sigma bonds in the reactants (C14-C15) become shorter in the transiton states. These bonds resulted in almost equal bond lengths of 1.39±0.01 Å, which indicates the presence of delocalised electrons, and thus, a cyclic transition mechanism. The terminal carbon bonds (C1-C10/C2-C13) have a bond lengths of 2.29 Å and 2.27 Å in the exo and endo transition states respectively. Bear in mind that the typical sp3 C-C bond lengths are 1.54 Å, while typical sp2 C=C bond lengths are 1.32 Å, while the Van Der Wall radius of the carbon atom is 1.7 Å. The bondlength of the partly formed σ C-C bonds in the Transition Structure (2.27 Å), is more than the typical C-C bond length, but less than twice the Van Der Wall radii of carbon atoms. This suggests that there is an overlap of the Van Der Waals radii between the two terminal carbon atoms, leading to the partially formed σ bonds. As seen from the transition structure, these partially formed bonds are of equal length, furher proof that this Dies Alder Reaction is a concerted, synchronous reaction. The most notable difference between the bond lengths of the exo and endo transition structures are the bond lengths between the terminal carbons which form the sigma bond C1-C10/C2-C13, which is 2.29 Å in the exo structure and 2.27 Å in the endo structure. This difference in bond length is because the endo Transition State would be more sterically hindered than the Exo Transition State. This is due to the C=O fragments in Maleic Anhydride, which, in the Exo TS, is oriented towards the less hindered Pi orbitals of the CH2CH2 fragment, whilst in the Endo state, the C=O bonds of Maleic Anhydride is oriented close to the sterically hindered CHCH bridge. This is counter-intuitive, as the Energy of the Endo state is lower than the Exo State. However, this irrgularity can be explained by, Secondary Orbital Overlap which is explained in the next section. HOMO and LUMO comparison of Reactants and Transition States Cyclohexa-1,3-diene .chk Maleic Anhydride .chk Exo Transition State .chk Endo Transition State .chk LUMO E= -0.01511 Antisymmetric E= -0.03116 Antisymmetric E= -0.07840 Antisymmetric E= -0.06769 Antisymmetric HOMO E= -0.20103 Antisymmetric E= -0.26437 Antisymmetric E= -0.24216 Antisymmetric E= -0.24232 Antisymmetric

It was observed that the HOMO/LUMO of the reactants and the transition states are all antisymmetrical to the plane of symmetry bisecting the structures. Determining the HOMO/LUMO responsible for these transition structures via the rules of symmetry is not possible. However, investigating the energies of the frontier orbitals yield an interesting observation.

It was observed that the energy gap between the HOMO of cyclohexadiene and LUMO of Maleic Anhydride was much smaller (0.16987 a.u.) than the energy gap between the LUMO of cyclohexadiene and HOMO of Maleic Anhydride (0.24926 a.u.). As the energy gap determines the rate of the reaction, the main frontier orbital interaction is that of the HOMO of cyclohexadiene and LUMO of Maleic anhydride. This reaction follows a normal electron demand due to the large electron-withdrawing effect of dienophile Maleic Anhydride, which has electron withdrawing C=O bonds and electronegative O atoms, and the electron donating capabilities of the electron-rich cyclohexadiene. The HOMO of cyclohexadiene and LUMO of Maleic Anhyrdide are both assymetric with respect to the plane of symmetry, which results in the observed assymetric HOMO of the transition states.

The reason why the energy of the Endo Transition State is lower than the Exo Transition State is due to an effect named the Secondary Orbital Overlap. It is defined as the positive overlap of a nonactive frame in the frontier molecular orbitals of a pericyclic reaction.

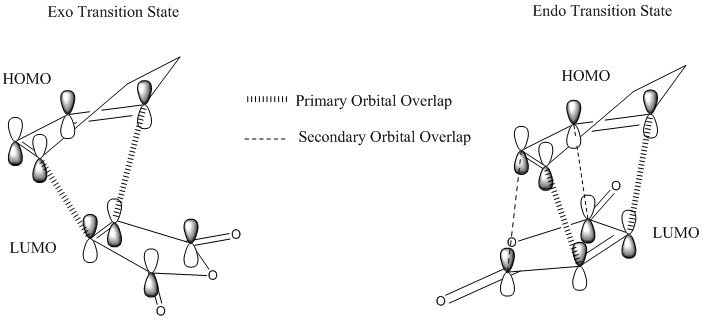
As seen in the above diagram, there is an additional overlap in the frontier orbitals of the reactants when assuming the Endo transition state, while this secondary interaction is absent in the Exo Transition State. These interactions lower the energy and stabilize the Transition State, thus, the ativation energy from teh reactants to the Endo Transition State is smaller than to the Exo Transition State. Thus, this Dies Alder Reaction selectively produces the Endo product through kinetic control.

Further Discussion

In a normal demand Diels–Alder reaction, the dienophile has an electron-withdrawing group in conjugation with the alkene; in an inverse-demand scenario, the dienophile is conjugated with an electron-donating group. This inverse demand Dies Alder reaction mechanism was not explored in this computation. By changing the reactants to an electron-rich dienophile and an electron-poor diene, the inverse demand mechanism could be investigated through computational methods. This is particularly useful because inverse demand Diels Alder reactions often involve heteroatoms, and can be used to form heterocyclic compounds. This makes itparticularly useful in natural product syntheses, where the target compounds often contain heterocycles.

Another factor in the Diels Alder reaction that was not investigated was the effects of regioselectivity. The Diels Alder reactions used in this computational experiment were all symmetrical, thus regioselectivity was not an issue. However, introduction of electron withdrawing and electron donating groups could alter the regioselectivity of the reaction, which could have been investigated computationally via FMO analysis.

Other factors that could have been considered include solvent effects and thermal activation, which may alter the preference of a specific transition state. These calculations may be possible by altering the temperature in Gaussian, or changing the solvent options from "none" to a solvent.