Jump to content

Rep:Mod:ickm1320

From ChemWiki

Module 2 - Bonding in Inorganic Chemistry

Computational Inorganic report by Keith Moore

Introduction

Bonding in chemical systems often diverges from the familiar 2-centre-2-electron bond widespread in chemistry texts, and sometimes the very existance of bonds in even simple structures can be called into question. In order to better understand structure in a selection of molecules, a computational approach will be taken to asseses vibrational modes, molecular orbitals and natural bond orbitals.


Optimisation

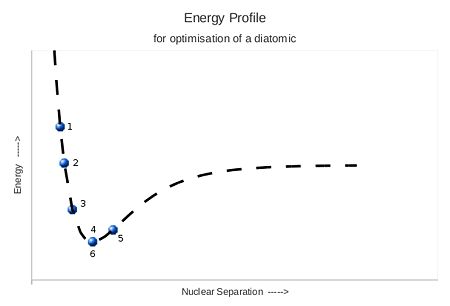
Before properties are computed it is important to ensure that the geometry of the structures studied correlate with an energy minimum. That is to say that the atoms are in an equilbrium position associated to the stable configuration of that molecule. When searching for this equilibrium postition, Gaussian begins by calculating the energy of the initial state using the chosen method. It then distorts the molecule slightly and recalculates the energy. These energies are compared, and the structure with the lower energy is chosen. Gaussian then continues with this process, lowering the energy until a minimum is found. This concept is illustrated for a simple diatomic system.


Positions 1 to 4 see the energy decreased as the separation is increased. When increased too much, at 5, the system is returned to the lower previous value 6


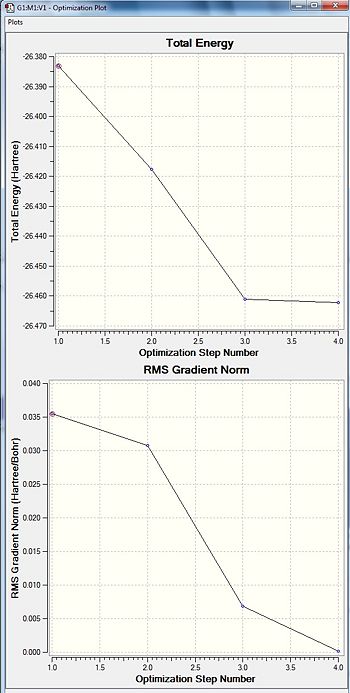
To ensure that a minimum is found, Gausian analyses the gradient of the potential energy surface to ensure that it has reached zero. This can be seen through the GaussView interface as charts of Energy and Gradient against the iteration number.



Vibration Analysis

When Gaussian performs a frequency analysis, it is calculating the ways in which the molecule oscillates about its equilibrium position. This can alternatively be thought of as the second derivative of the potential energy surface of the molecule. The second derivative provides information on the nature of the system about it's equilibrium position. If all the normal modes are positive, then the system is at a minimal stationary point i.e. the system is definitely at an energy minimum. When looking at ground states, negative frequencies are indicative of mistakes in the input. However negative values in the "low frequency" output, which arise through the motion of the molecule's centre of mass, are to be expected so long as they are of a suitably low value.

Vibrations arise due to a "restoring force" exerted on atoms as they are displaced from the equilibrium position. This restoring force is suggestive of bonding within a system, and it's strength gives a good indication of the strength of the bond. So, by analysing the shape and frequency of a vibration, much information can be gained on the nature of bonding in a system.

Molecular Orbital Analysis

Natural Bond Orbital Analysis

Borane, BH3

Boron hydrides form an extensive range of cluster structures, that are electron deficient and behave as Lewis acids . The parent structure to these compounds is BH3, however it is too unstable and so the simplest of the boranes is diborane, B2H6[1].

Although too reactive to form, monoborane can be investigated computationally to gain an understanding of its bonding and structure. A D3H BH3 structure was constructed using GaussView. This structure was then submitted for optimisation using B3LYP/3-21G. Frequency, MO and NBO analysis was then performed on the optimised structure.


Vibrational Frequency Analysis

A frequency calculation, using B3LYP/3-21G, was performed on BH3 to check that it had definitely reached a minimum. Relatively high low frequencies were observed at up to -67cm-1. Although these values are very large for the low frequencies, they are still relatively small in contrast to the lowest normal mode observed at 1144cm-1, and are likely to have arisen through the use of an a low level method / basis set combination.


Table of Vibrational Modes in BH3
Illustration Mode No. Frequency / cm-1 IR Intensity / km mol-1 Symmetry under D3h Type
1 1144 93 A" Symmetric Bend
2 1204 12 E' Degenerate Bend
3 1204 12 E' Degenerate Bend
4 2598 0 A' Symmetric Stretch
5 2737 104 E' Degenerate Stretch
6 2737 104 E' Degenerate Stretch


Molecular Orbitals

A full population analysis was performed, using B3LYP/3-21G, with additional NBO analysis, to analyse the bonding in BH3 in terms of its molecular and natural bond orbitals.

Molecular Orbitals of BH3
MO diagram Molecular Orbital Orbital Energy/a.u.

0.192

0.189

-0.075

-0.357

-0.518

-6.730


Comparing the LCAO molecular orbitals produced through a LCAO approach to the computationally generated MOs, it can be seen that they serve as good "cartoons" of the complete MOs. Although the localised lobes shown in the LCAO approach do not correlate well with the more diffuse view seen computationally, seen particularly in the e` examples, if in-phase interactions were shown "joined up" then the LCAO cartoons would be incredibly close to the true molecular orbitals.

This supports the LCAO approach as a method of MO generation, since a strong qualitative picture of the bonding in a compound can be produced using a pen and paper. However the LCAO approach is held back quantitatively as demostrated by the orbitals 2e`, 3a1`. LCAO managed to predict well the shape of MOs, but failed to offer any substantial prediction of the energy of the orbitals. Instead approximations had to be made based on the in-phase and out-of-phase interactions between the combined AOs, and so the 3a1` orbital was incorrectly predicted to be lower in energy than the degenerate 2e` orbitals.


Natural Bond Orbitals

The key result from the NBO analysis in this case are the charges on the atoms. An increase in negative charge is seen on all three hydrogen atoms, leaving the central boron atoms electron deficient.

Looking more closely at the results from the NBO analysis, it can be seen that three bonds exist, one between the boron and each of the hydrogen bonds. Each of these bonds is 33.3% s in character and 66.7% p in character. Thus, it can be seen that the boron form three sp3 hybrid orbitals with the hydrogens. The bond is biased by 55.5% toward the hydrogen, resulting in the charge distribution already noted.


Thallium (III) Bromide, TlBr3

Thallium (III) Bromide can be prepared through combination of its respective elements[2]. However it is unstable and will decompose to ThBr and bromine gas at room temperature.

As thallium is incredibly toxic analysis of TlBr3 computationally is advantageous, since properties of its compounds can be predicted prior to synthesis. If no useful properties are predicted in a compound then the risk of its use can be avoided.

The molecular structure of thallium bromide, TlBr3 was optimised using the B3LYP method and the LANL2DZ basis set.

After optimisation each Tl-Br bond was 2.65 Å and the Br-Tl-Br bond angle was 120°. Xray studies have shown TlBr3 to have a bond length of 2.564 Å[3], which compares favourably to the computationally obtained result suggesting that the the simulation is a reasonable model of the system.


Vibrational Analysis

Frequency analysis was carried out on the optimised TlBr3 structure again with the B3LYP/LANL2DZ setup. It is important to maintain the same methods and basis sets, as each setup will have different parameters for any variables, and so will produce different results. Upon changing methods it would be likely that the system was no longer at a minimum, leading to negative frequencies.


Vibrational Modes of ThBr3
Illustration Mode No. Vibrational Frequency / cm-1 Intensity / km mol-1 Symmetry Type
1 46 4 E' Degenerate Bend
2 46 4 E' Degenerate Bend
3 52 6 A2" Symmetric Bend
4 165 1 A1' Symmetric Stretch
5 211 3 E' Degenerate Stretch
6 211 3 E' Degenerate Stretch


Miniproject-Group 15 Sulphur Cages

Combinations of the group 15 elements with sulphur of the form X4S4 (where X is a group 15 element), are capable of forming a series of analogous cage structures. However the nature of the bonding within the cage structure is seen to change as the group is descended.

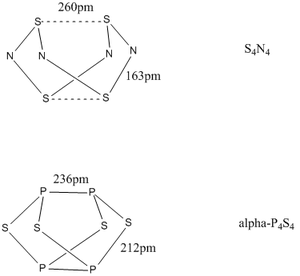
S4N4 is an eight membered ring with a puckered structure. However the S-S contact distance is found to be 2.60 Å[4]. This is reasonably close to 2.06 Å, the sum of the covalent radii[4] for two sulphur atoms, and so it could be suspected that there may be some bonding interaction present between opposite sulphur atoms in this system.

The S-N bonds are also of interest as they are only 1.63 Å, which is significantly shorter than the sum of the covalent radii, 1.78 Å, suggesting that the bonds might be slightly more than singly bonded.

In contrast, P4S4 does not have the S-S contacts shown in S4N4, but rather the phosphorus atoms opposite each other are formally bonded to each other to form a cage like structure. The bond distances in this case are 2.36 Å for the P-P bonds and 2.12 Å for the P-S bonds[5]. The P-S length is almost identical to the sum of the P-S covalent radii, 2.13 Å, but the P-P distance is quite long compared to the covalent radii sum, 2.20 Å[4].

The aim of this miniproject is to investigate the MOs and NBOs of these cage structures to compare the nature of the bonding in the two systems, and to see where the differences in bonding arise.

Gaussview was used to build the structures for the two cage compounds, with particular attention to the interatomic distances. The structures were constrained to C2v symmetry, and optimised using B3LYP/6-311G(d). Frequency analysis was performed to ensure the energy had been minimised, and a full population analysis was performed with NBO analysis also.

Molecular orbital analysis for S4N4. Note that low lying core orbitals not involved in bonding are not displayed.


Molecular Orbital Analysis for S4N4
Illustration MO Energy / amu Symmetry under C2v Comment MO Energy / amu Symmetry under C2v Comment
HOMO -21 -1.04 A1 Continuous loop of σ orbital density following shape of molecule HOMO -9 -0.44 B2
HOMO -20 -0.98 B1 two lobes of σ density extending across 1 sulphur and 2 nitrogen atoms. HOMO -8 -0.40 B1
HOMO -19 -0.98 B2 two lobes of σ density extending across 1 sulphur and 2 nitrogen atoms. HOMO -7 -0.40 B2
HOMO -18 -0.87 A2 orbital density extending from N atoms toward S atoms, with phase change over S HOMO -6 -0.36 B1
HOMO -17 -0.83 A1 orbital density extending from S atoms toward N atoms, with phase change over N HOMO -5 -0.36 B2
HOMO -16 -0.69 B2 σ ring with six nodes HOMO -4 -0.33 A1
HOMO -15 -0.69 B1 σ ring with six nodes HOMO -3 -0.31 A2
HOMO -14 -0.56 A2 σ ring with 8 nodes HOMO -2 -0.29 A1
HOMO -13 -0.55 A1 σ bonding interaction across Sulphur contacts, with opposite phase lobes on the Nitrogen atoms HOMO -1 -0.28 A2
HOMO -12 -0.51 A1 HOMO -0.27 A1
HOMO -11 -0.50 A1 LUMO -0.13 B1
HOMO -10 -0.44 B1 LUMO +1 -0.13 B2

Appendix

References

  1. ↑ P. Atkins, T. Overton, J. Rourke, M. Weller, F. Armstrong, in Inorganic Chemistry, ed. Oxford University Press, Oxford, 4th edn., 2006
  2. ↑ E. Wiberg, N. Wiberg, A. F. Holleman, in Inorganic Chemistry, ed. N. Wiberg, Academic Press, California, 2001, pp. 1033
  3. ↑ J. Glaser, G. Johansson, Acta Chem. Scand., Ser. A, 1982, 36, 125-135, DOI:10.3891/acta.chem.scand.36a-0125
  4. ↑ 4.0 4.1 4.2 C. Housecroft, A. G. Sharpe, in Inorganic Chemistry, ed. Prentice Hall, 3rd edn., 2008
  5. ↑ A. M. Griffin, P. C. Minshall, G. M. Sheldrick, J. Chem. Soc., Chem. Commun., 1976, 809-810 DOI:10.1039/C39760000809
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:ickm1320&oldid=819540"