Rep:Mod:hyl314MgO

The Free Energy and Thermal Expansion of MgO

Introduction

In this assignment, the thermal expansion and of MgO and its thermal expansion coefficient are computed by the quasi-harmonic approach and the molecular dynamic approach.

Thermal expansion coefficient is defined by the equation $\alpha =\frac{1}{V_0}{\left(\frac{\partial V}{\partial T}\right)}_p$ and can therefore be found if the temperature dependence of cell volume and the initial cell volume are known.

MgO has a crystalline solid with a face-centred cubic unit cell, the ions are held together by the strong ionic interactions between the Mg²⁺ and O^2- ions.

Phonon modes of MgO

Phonon dispersion curves and the density of states were computed for various grid size in order to find out an appropriate grid size for the free energy calculation using the quasi-harmonic model.

Phonon dispersion curve and DOS of grd size 1x1x1

Grid size	Phono dispersion curve	Density of states
1x1x1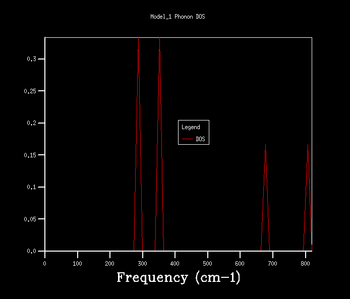

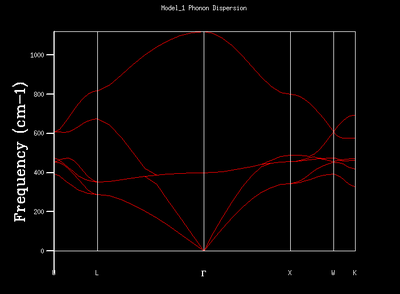By comparing the frequencies in the DOS and the phonon dispersion curve, it can be seen that the k point responsible for the DOS of 1x1x1 grid is at symmetry point L which corresponds to (0.5, 0.5, 0.5) fractional coordinates in reciprocal space. The intensities at the 2 lower frequencies are doubled as there are 2 overlapping acoustic branches passing through them in the phonon dispersion curve due to symmetry.

Grid size	Density of states	Grid size	Density of states
2x2x2		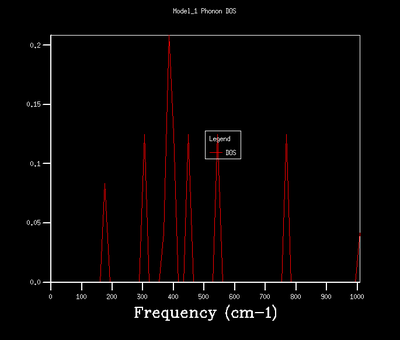16x16x16
3x3x3		32x32x32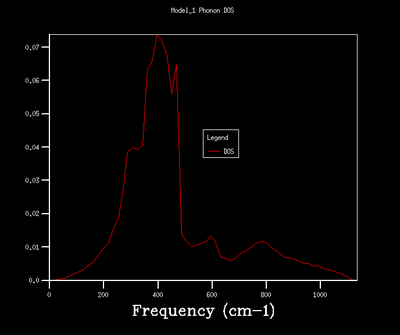
8x8x8		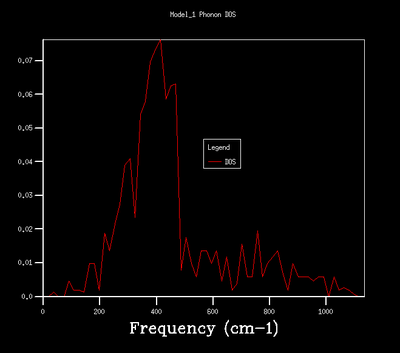64x64x64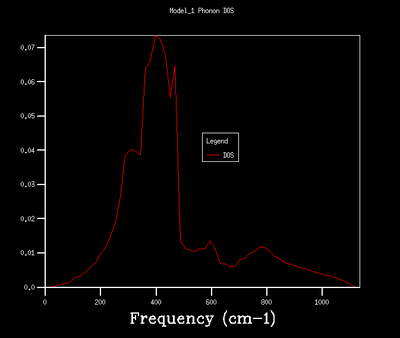

As shown in the above table, an increase in grid size leads to a smoother and more comlicated DOS due to more k points, and therefore vibrational modes, being included in the calculation. A grid size of 32x32x32 was chosen for the quasi-harmonic calculation as it provides a smooth and continuous DOS without being too computationally expensive. It produces a less noisy DOS when compared to 16x16x16 grid size as indicated by the smooth appearance. The DOS of 32x32x32 and 64x64x64 grid sizes show the same general shape with the latter one in a higher resolution.

The same grid size of 32x32x32 can be used to model CaO as the two oxides have similar primitive cells and the same number of atom per unit cell. Crystals with more than 2 atoms in their primitive cells, such as Zeolites, requires a smaller grid size as an increase in the size of primitive cell leads to a decrease in size in k-space so less k-points has to be sampled to achieve the same level of accuracy. The same applies to regular metals such as lithium as the delocalised electrons in the lattice screens repulsions between the metal cations, resulting in more dispersed bands so less k-points and therefore a smaller grid size is needed to produce a DOS with a similar level of accuracy.

Free Energy of MgO

The free energy of MgO was computed using the quasi-harmonic model as a sum over all the vibrational modes. The free energy initially increases with the grid size as more k points and therefore more vibrational states are sampled. The difference between the free energy calculated using different grid size decreases as the grid size increases until it reaches a constant at 32x32x32 grid.

Grid size	Helmholtz free energy (eV)	ΔA (eV)
1x1x1	-40.930301
2x2x2	-40.926609	3.692E-03
4x4x4	-40.926450	1.590E-04
8x8x8	-40.926478	-2.800E-05
16x16x16	-40.926482	-4.000E-06
32x32x32	-40.926483	1.000E-06
64x64x64	-40.926483	0

The accuracy each grid size can achieve in a calculation can be estimated using ΔA, an accuracy of 1 meV corresponds to a ΔA in the order of 10^-3 and can therefore be achieved by a 4x4x4 grid. An accuracy of 0.1 meV is therefore achieved by 8x8x8 grid which has a ΔA in the order of 10^-4 while that of 0.5 meV is achieved by an intermediate grid size of 6x6x6.

A grid size of 32x32x32 is used for the investigation of the temperature dependence of the Helmholtz free energy, cell volume and parameter by running the calculations at 0-1000 K with an interval of 100 K.

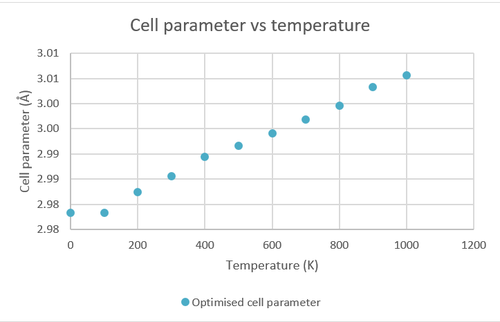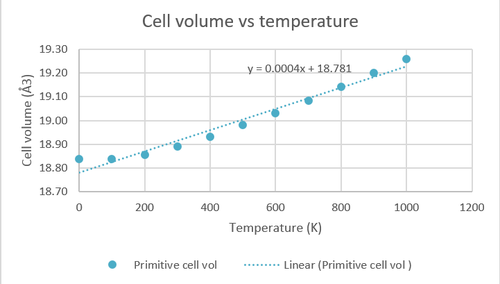
As seen from above, the Helmholtz free energy of MgO decreases with increased temperature. This trend agrees with the equation of Helmholtz free energy (A=U-TS) as an increase in temperature leads to an increase in the second term which is always positive (entropy is always positive) resulting in a more negative Helmholtz free energy, this effect is amplified by the increase in entropy caused by an increased temperature. The opposite is true for cell volume and cell parameter as they increase with an increased temperature.

The thermal expansion coefficient was calculated using the equation $\alpha =\frac{1}{V_0}{\left(\frac{\partial V}{\partial T}\right)}_p$ where ${\left(\frac{\partial V}{\partial T}\right)}_p$ is the gradient of the line of best fit in the cell volume against temperature graph. This gradient is divided by the initial cell volume in order to obtain an intrinsic property which is independent of the amount of matter.Using the method mentioned above, the thermal expansion coefficient was found to be 2.124x10^-5 K^-1 which is a close approximate to the literature value (3.706x10^-5 K^-1).

Molecular Dynamics

The thermal expansion coefficient can also be found using molecular dynamics in which all atoms in a system are given a velocity and allowed to move accordingly following Newton's second law (F=ma). The loss of periodicity of movements means that a larger number of cell is required for this method and a supercell of 32 MgO units is used.

As with the quasi-harmonic model, the thermal expansion coefficient can be found by dividing the gradient of the change in cell volume per formula unit with respect to temperature by the initial cell volume. The coefficient obtained is 2.654x10^-5 K^-1 and is a closer match to the literature value.

From the above graph, it can be seen that both approaches show the same general trend where the cell volume increases with temperature. The two sets of data do not overlap perfectly but seem to converge as the temperature increases. This disagreement is likely to be caused by the difference in the nature of movements between the two models where movements in the quasi-harmonic approach are periodic and can be modelled by a primitive cell and that in molecular dynamic approach are non-periodic and the random movements have to be modelled by a supercell of which the size is limited due to a large supercell being computationally expensive to operate.

Conclusion

Both the quasi-harmonic and molecular dynamic approach provide a fair estimate of the thermal expansion coefficient of MgO with the later one giving a better approximation that lies closer to literature value. They also predict the same general trends of the temperature dependence of Helmholtz free energy and cell volume where the former one decreases with increasing temperature and the later one decreases as the temperature increases.

Thermal expansion is caused by the increased kinetic energy provided by the increased temperature allowing higher energy vibrational modes to be accessed. As more atoms in the crystal are in these high energy vibrational states, the repulsive interactions and therefore the distance between them increases, leading to thermal expansion.

The quasi-harmonic model fails at high temperature close to the melting point of MgO as bond breaking, which would normally occur when a solid melts, is not allowed in this model and is therefore not a good reflection of reality. The opposite is ture for the molecular dynamic model which is a poor approximation at low temperature due to its classical nature which fails to take into account of the zero point energy.