Rep:Mod:hweioe4yvn45
Introduction
Using modern computation techniques it is possible to model organic structure, predict reactivity, rationalise outcomes of reactions and predict improvements and modifications. Firstly, molecular mechanics will be used geometry and regioselectivity and secondly semi-empirical and DFT molecular orbital theory to investigate regioselectivity and neighbouring group participation. Finally, investigate a recent journal article which contains regioisomers, and rationalise there assignment using a number of computational techniques.
Modelling using Molecular Mechanics
The Hydrogenation of Cyclopentadiene Dimer
Dimerisation of cyclopentadiene
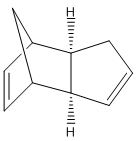
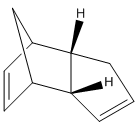
Molecular mechanics force field calculations (MM2 using ChemBio3D) can be applied to molecules to find their lowest energy conformers or isomers. In this investigation the dimer of cyclopentadiene (dicyclopentadiene) shall be modelled to help understand the mechanism.
Cyclopentadiene has been shown to undergo rapid Diels-Alder cycloaddition with itself at room temperature to form a dimer.[1]The reaction is stereospecfic, exclusively producing the endo dimer.[2]
| Dimer | MM2 Energy kcal/mol | Stretching | Bending | Torsion | van der Waals | Hydrogen bond |
|---|---|---|---|---|---|---|
| Molecule 1 | 31.9 | 1.29 | 20.6 | 7.63 | 4.24 | 0.377 |
| Molecule 2 | 34.0 | 1.28 | 20.8 | 9.50 | 4.28 | 0.444 |
The above molecular mechanics result show that the exo cyclopentadiene dimer is thermodynamical more stable than the endo form. The energy difference comes from the increased torsional strain (1,4 interactions) that the endo form incurs across the two new C-C. In the endo dimer the C-C-C-C have a dihedral angle of 50 and -47 degrees, whereas the exo forms dihedral angle is 178 and 177. The angles are roughly gauche and antiperiplanar respectively. Thus, the endo form suffers from more torsional strain as gauche is less energetically favourable than antiperiplanar.
It is unlikely that the reaction is thermodynamically controlled and under equilibrating conditions as the most stable product is not formed at all in the course of the reaction. Baldin et al [3] observed that upon gentle heating endo dimer converts to the exo dimer, showing that the exo dimer is more thermodynamically stable.
In 2002 Caramella et al[4] showed that the formation of endo dicyclopentadiene progressed kinetically through a bispericyclic transition structure. These results from Caramella et al also show the presence of attractive secondary orbital interactions (SOI) and which also support the endo product being formed. The less stable endo product is also predicted by Alder's "endo rule"; where the most stable transition state involves "maximum accumulation of double bonds". Furthermore, as the Diels-Alder cycloaddition is irreversible at room temperature, the reaction will progress rapidly through the pathway with the lowest activation energy. This results in a stereospecific reaction, in which only the kinetic product is formed.
To conclude dicyclopentadiene forms a dimer through a kinetic pathway as indicated by the MM2 calculations. However, any intricacies about that mechanism cannot be found by this calculation method and this is therefore a limitation of the method. A more complex computational treatment, such as the one performed by Carmella et al, could be performed to help elucidate the mechanism.
Hydrogenation of Cyclopentadiene
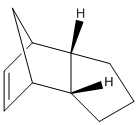
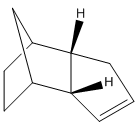
The next experiment involves the hydrogenation of endo dicyclopentadiene. During the hydrogenation firstly a specific dihydro derivative is formed before saturating fully to the tetrahydro derivative. The two possible dihydro derivatives are shown below along with their calculated energies.[5]
| Molecule | Total | Stretching | Bending | Torsion | van der Waals | Hydrogen bond |
|---|---|---|---|---|---|---|
| 2 | 34.0 | 1.28 | 20.8 | 9.50 | 4.28 | 0.444 |
| 3 | 35.7 | 1.28 | 19.8 | 10.9 | 5.6 | 0.162 |
| 4 | 31.2 | 1.1 | 14.5 | 12.5 | 4.5 | 0.142 |
From the MM2 calculations it can be clearly seen that 4 is thermodynamically more stable than 3 (and even 2). Thermodynamically molecule 4 is more stable as the double bond in the norbornene ring has been hydrogenated; the bond is now longer, reducing the stretching and bending strain in the very stressed bicyclic system. The reduction in bending and stretching strain is more than if the cyclopentene ring had been saturated. The result is that molecule 4 is more stable than 2 or 3. Therefore, 4 is the thermodynamically favoured product of hydrogenation.
Hydrogenation of 2 to 3 is a thermodynamically unfavourable process. Molecule 3 has an increase in adverse 1,4 steric interactions (torsion and 1,4 VDW) compared to 2, from the newly hydrogenated double bond; the magnitude of which is larger than the reduction of strain in the cyclopentane system.
Zoua et al[6] have shown that the double bond in the norbene ring is longer, has a smaller vibrational frequency and lower bond order than the double bond in the cyclopentene. Its comparitive weakness means it has a lower activation enthalpy of hydrogenation. Therefore, 4 is the kinetically favoured dihydro derivative as well.
To conclude molecules 4 is the thermodynamically favoured product, from MM2 calculations and the kinetically favoured product from the literature.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
Alkylation of Pyridinium Ring in Molecule 5 with Grinard reagents
The nucleophilic addition of a methyl group from a Grignard reagent to a pyridinium ring in molecule 5 proceeds with interesting regio- and stereochemistry. Schultz et al hypothesised the mechanism below. [7]

Schultz et al postulated that the unusually high regio- and stereoselectivity was from the electronegative amide oxygen coordinating with the electropostive magnesium of the Grignard reagent. Due to the rigid positioning positioning of the amide oxygen, lead to the Grignard regagent always coordinated in a particular manner, in turn leading to a regio- and stereoselective alkylation of the pyridium ring.
The aim of this experiment is investigate this postulate for molecule 5. This can be done by modelling different conformations of molecule 5 (i.e. positions of C=O) using MM2 calculations, to find with conformers are the lowest energy and therefore the relative positioning of the amide O.
| Dihedral angle (o) | Energy of conformer (kcal/mol) |
|---|---|
| 9 | 43.1429 |
| 9 | 44.1174 |
| 12 | 43.1446 |
| 18 | 46.0511 |
| 23 | 44.7376 |
| 34 | 193.8915 |
| 122 | 168.2197 |
From the table is becomes clear that there are numerous low energy conformers between the dihedral angle of 9-23. Therefore, the C=O will spend time at all of these conformations. All of these angles and positive and therefore the coordination of the C=O---Mg will result in the methyl undergoinng nucleophilic addition to the same face of the pyridinium ring. Helping to prove the postulated proposed by Schultz et al.[7]
N. B. on inclusion of MeMgI in the MM2 calculation, ChemBio3D cannot complete the calculation and instead brings up an error - molecular mechanics parameters are available only for certain types of bonds, and frequently are not available for many functional groups. Metal ions are also a category less easily handled at present by this type of model. Molecular mechanics calculates in values by using predefined force constants for bonds and therefore unless is already has the values set it cannot calculate them.
Derivitisation of Pyridinium Ring in Molecule 7 with Aniline
In a similar manner to that above Leleu et al[8] noted that the below reaction scheme progressed with high regio- and stereoselectivity. However, Leleu et al observed the amine attack on the opposite face to the C=O. They attributed this to steric control by the C=O group, i.e. it blocked incoming amines on the it's face and therefore directed tem to the opposite face.
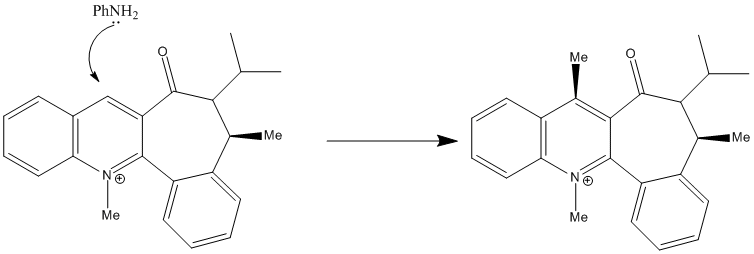
Similarly to above the MM2 can be used to find low energy conformations. The aim of this experiment is investigate this observation for molecule 7. This can be done by modelling different conformations of molecule 7 (i.e. positions of C=O relative to the ring) using MM2 calculations, allowing the observation to be checked.
| Dihedral angle (o) | Energy of conformer (kcal/mol) |
|---|---|
| -21 | 63.4265 |
| -20 | 63.4751 |
| -19 | 66.3836 |
| 23 | 84.1319 |
| 56 | 44.7376 |
The equilibrium conformation is likely to have an angle between the C=O and pyridium ring of approximately -20o. At this angle the C=O is positioned above the ring and prevents the attack on this face. As can be seen by this jmol.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol.
Stereochemistry in 9 & 10
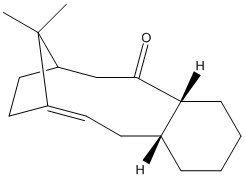
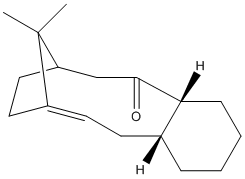
Atropisomerism is a type of stereoisomerism, where a high barrier of rotation about a single bond allows the sepearate conformers to be isolated.[9]. Paquette et al showed in their total synthesis of taxol the intermediate 9 and 10 were atropisomers, with 9 inter converting to the more energetically stable isomer 10 on standing.[10]
 |
 |
| Atropisomer | MMFF94 energy | MM2 energy | Stretching | Bending | Torsion | van der Waals | Hydrogen bond |
|---|---|---|---|---|---|---|---|
| Molecule 9 | 70.6 | 48.9 | 2.68 | 15.8 | 18.2 | 12.7 | 0.146 |
| Molecule 10 | 60.6 | 44.3 | 2.56 | 19.8 | 12.6 | 12.6 | -0.181 |
The optimised structure of 10 is the lowest energy isomer of the intermediate according to MMFF94 and MM2 calculations. In both atropisomers the 5 & 6 membered rings adopt the same favourable conformations, twisted envelope and chair respectively. In contrast the Paquette et al reported the 6 membered ring adopts higher energy twist boat of 9 and chair conformation for 10.
The differences in energy between the two atropisomers are that 10 has smaller torsion energy and a negative H-bond interaction, while 9 has a smaller bending energy. Therefore, the difference in energy comes mainly from the 9 membered ring conformations and the orientation of the carbonyl and double-bond functionalities.
Unusual stability of intermediates 9 & 10
It was noted in the synthesis of Taxol, by Paquette at al, that the alkene of 10 reacted unusually slowly in the subsequent reactions. By comparing the MM2 force field energies of 10 and the dihydro 10 derivative it is possible to investigate why the alkene is strangely unreactive.
 |
 |
| Dihydro derivate | Total | Stretching | Bending | Torsion | van der Waals | Hydrogen bond |
|---|---|---|---|---|---|---|
| Molecule 10 | 44.3 | 2.56 | 10.8 | 19.8 | 12.6 | -0.181 |
| Molecule 10 dihydro | 60.3 | 3.40 | 19.2 | 21.2 | 15.5 | 0.00 |
More conformers of 10 dihydro derivative were calculated, but all the values for the force field energy were considerably larger above energy than the above conformer.[11]
On initial inspection it can be seen that 10 has a lower total energy than the the lowest energy 10 dihydro-derivative conformer. The biggest difference in calculated energies for 10 is in the torsion energy. The increase in torsion energy is from the increased 1,4 interactions from the newly saturated bond. The torsion energy increases quite dramatically as the 1,4 interaction is between a new hydrogen and a dimethyl bridging unit, and across the newly saturated bond.
This molecule is an example of a hyperstable alkene, i.e. an the olefin has a negative strain energy compared to the parent hydrocarbon[11]. They tend to occur around bridgehead groups of medium polycyclic rings.[12] Molecule 10 fulfils both of these criteria and therefore can be labelled as a hyperstable olefin. With its unusual stability explaining the observation of Paquette et al that the alkene was slow to react.
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
Part 1 - MO description of Molecule 12
9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene (molecule 12) has been reported to show remarkable π-selectivity when reacted with electrophilic reagents, such as dichlorocarbene or peraacid.[13]
For examples for dichlorocarbene adds to the double bond syn/endo to the chlorosubstiuent of molecule 12 regioselectivity, only the syn/endo mono adduct is detected. The reaction scheme is shown below.[14]
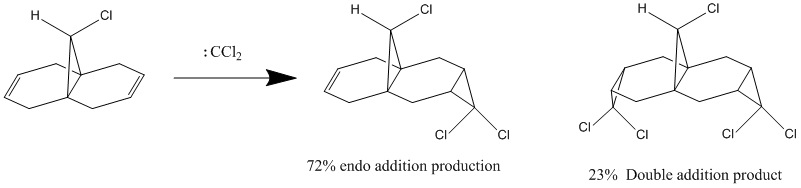
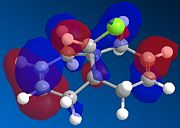
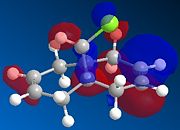
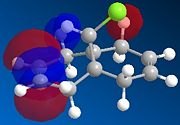
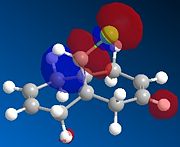
MOPAC/PM6 calculations were run on molecule 12, this treatment yielded the calculated molecular orbitals of 12, allowing further investigation into why the addition is regiospecific. The orbitals surrounding the HOMO (highest occupied MO) and LUMO (lowest unoccupied MO) are shown below as these orbitals affect the reactivity of a molecule to electrophilic addition, as the HOMO is the orbital which will be donating electrons to the incoming electrophile to form new bonds and complete the reaction.
| HOMO-1 | HOMO | LUMO | LUMO+1 | LUMO+2 |
|---|---|---|---|---|
 |
 |
 |
 |
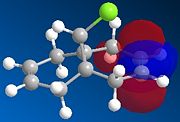 |
Initial observation of the HOMO shows that the syn-alkene has a significantly higher electron density compare to the anti-alkene, making the syn-alkene more nucleophilic. The result of which is that the electron deficient dichlorocarbene will react preferentially with the electron rich syn-alkene, as the syn-alkene can donate the required electron density to perform an electrophilic addition. It can also be seen that the more stable HOMO-1 has high electron density and therefore can react with an electrophile, after the syn-alkene, but this requires more forcing conditions.
Halton et al have reported similar results using PM3 calculations.[13] Furthermore, they speculated that the anti-alkene with its banana shaped π-MO's (HOMO-1) is more stable than the syn-alkene π-MO (HOMO)due to a favourable overlap between itself and C-Cl σ* (LUMO+1 but is LUMO+2 in lit.[13]).
One would expect that if HOMO-1 and HOMO are the anti- and syn-alkene π bonding orbitals then LUMO and LUMO+1 are the π* orbitals. However, LUMO+2 in our case is the π* on anti-alkene.
As noted above the results between Halton et al[13] and our results differ. The origin of this discrepancy is likely to be the relatively high symmetry of our flat molecule, compared to the puckered molecule reported in the lit. It is therefore likely that the C-Cl σ* is undergoing favourable overlap with another σ* orbital.
Part 2 - Vibrational frequencies of C=C double bonds and C-Cl
The vibrational frequencies of molecule 12 are influenced by the C-Cl bond, to calculate the influence DFT - B3LYP/6-31G(d,p) methods were applied to molecule 12 and syn-mono-alkene derivative.
 |
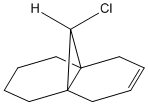 |
| Molecule | C-Cl Stretch | C=C Syn | C=C Anti |
|---|---|---|---|
| Molecule 12 | 772.62 | 1760.99 | 1740.88 |
| Molecule 12 syn-mono-alkene derivative | 779.93 | 1753.76 | - |
The value for C-Cl vibrational frequency for both molecules compares well to the lit. value of 780cm-1 [15]. Whereas, the alkenes vibrational frequency is somewhat higher than the lit. value of 1630-1680cm-1[16]. This suggests that the alkene is higher in energy than they should be and is likely to be from there strained cyclic nature.
The C-Cl bond becomes slightly higher in energy on removal on the anti-alkene, possibly due to the removal of favourable overlap between the C-Cl orbitals and anti-alkene orbitals. The syn-alkene also becomes lower in energy with the hydrogenation of the anti-alkene, with possibly the C-Cl σ* and syn-alkene undergoing increased overlap. It is therefore likely that the Cl-C σ* orbital stabilises both alkenes to a different extent due to amount of favourable overlap.
The vibrational frequencies of the syn- and anti-alkenes can be compared to show their relative strengths. The calculations show that the anti-alkene has a lower in vibrational frequency and therefore has a lower bond-energy than the syn-alkene, meaning it should be more reactive. This appear to be at odds with the results above, in which the syn-alkene reacts first. The difference can be explained by in two parts; firstly, vibrational frequency takes into account both σ and π contributions in the C=C, and secondly only π orbitals interact with incoming electrophiles. Therefore, the anti-alkene must have a relatively small C-C σ contributing (inductive effect of Cl) which means its bond is weaker than expected, but the π orbitals are still more stable than the syn-alkene π orbitals.
A possible improvement to this experiment would be to use a better basis set that covers the relative atoms more accurately. As using a too large basis set is like filling a fruitbowl with just watermelons, i.e. will not totally fill teh bowl. However, if you use a more representative basis set, a fruitbowl full of plums, apples, peaches, lemons and watermelons it can be a better fit and give more accurate results.
Another improvement would be to use a anharmonic oscillator to represent the bonds in the molecules, as using a harmonic oscillator brings in inherent errors due to simplicity and assumptions. An anharmonic oscillator model would make the calculations more accurate, but also require CPU power.
Part 3 - changing substituents on anti alkyne
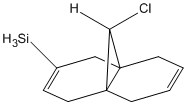
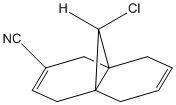
By changing the substituents on the anti-alkene one can investigate how the vibrational frequencies of molecule 12 change due to there different electronic properties.
 |
 |
 |
 |
| Molecule 12 Derivatives | C-Cl Stretch | C=C Syn/Endo | C=C Anti/Exo |
|---|---|---|---|
| Molecule 12 | 772 | 1760 | 1741 |
| -BH2 | 759 | 1756 | 1657 |
| -SiH3 | 763 | 1756 | 1690 |
| -CN | 765 | 1756 | 1706 |
| -OH | 766 | 1756 | 1657 |
All the substituents cause a weaken of the C-Cl and anti and syn C=C bonds, this can be noted from the decrease in vibrational frequency.
The electropostive -BH2 causes a weaken of the bond possibly due to the donation occurring into LUMO, which is the anti-alkenes antibonding orbital explaining the weakening of the anti alkene. Furthermore, the C-Cl bond σ* overlaps with the LUMO therefore the donation also occurs into the C-Cl σ* weakening the bond as well.
The same principle can be applied to the electropositive SiH3 and the resonance donating CN group. Which can donate electron density and stabilise the resulting positive charge. The OH group is both electron withdrawing and slightly resonance donating. The electron drawing property is the most important and causes a large decrease in anti-alkene bond strength but only a small decrease is C-Cl strength.
Mini Project
Introduction
It has been reported that cycloalkyl- and cycloalkenylbis-(phosphonates) have received attention as a possible class of pharmacologically active molecules.[17] They are seen as important alternatives to the closely related gem-diphosphonic acid derivatives, which have shown likelihood in becoming effective therapeutic options.[18] [19] [20]
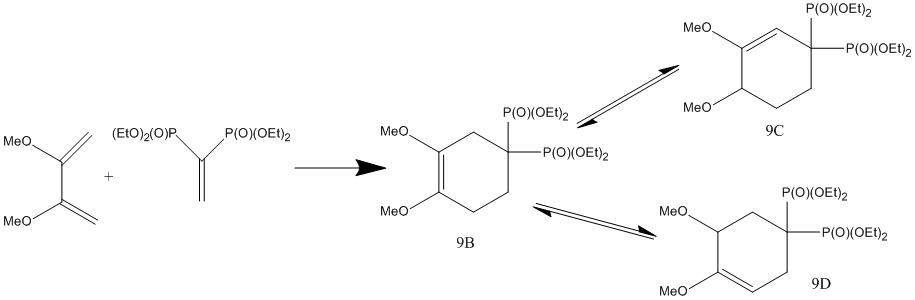
One synthetic route to cycloalkenybis-phosphonates is through the cycloaddition of vinyl-phosphonates and 1,3-dienes, which is the topic of Ruzziconi et al[21] paper. In this investigation we will analysis the NMR properties, IR and calculated energies of the regioisomers synthesised by Ruzziconi et al during their synthesis of cycloalkenylbis-(phosphonates) and check if their NMR assignments of their regioisomers are correct. With particular importance on the correct assignment due to potential pharmalogical nature of the resulting molecules.
The 3 regioisomers in question are shown in the reaction scheme below.
NMR comparison between Ruzziconi et al and calculated NMR spectra
All the following NMR spectra have been calculated in the following manner; firstly the molecule was drawn on ChemBio3D, the lowest energy conformer found using MM2, energy then minimized by MOPAC/PM6 calculated, energy minimized by DFT mpw1pw91/6-31g(d,p) calculations, the NMR was then calculated using the same DFT method as before.
The calculated NMR was then compared to the values reported by Ruzziconi et al.
NMR of regioisomer 9B
The spectrum produced by the calculations for molecule 9B is shown below.
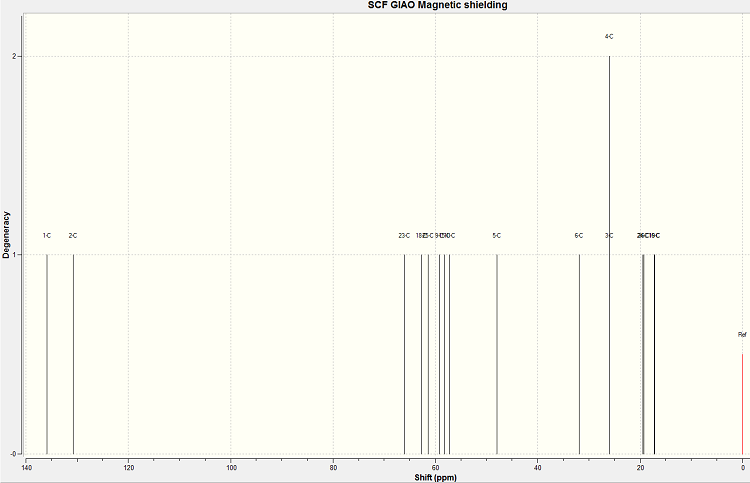
The assignment of the calculated and literature NMR spectra is shown below.
|
|
There are differences between the two chemical shifts values.

Analysis of the NMR data will follow at the end of the NMRs.
NMR of compound regioisomer 9C
The spectrum produced by the calculations for molecule 9C is shown below.
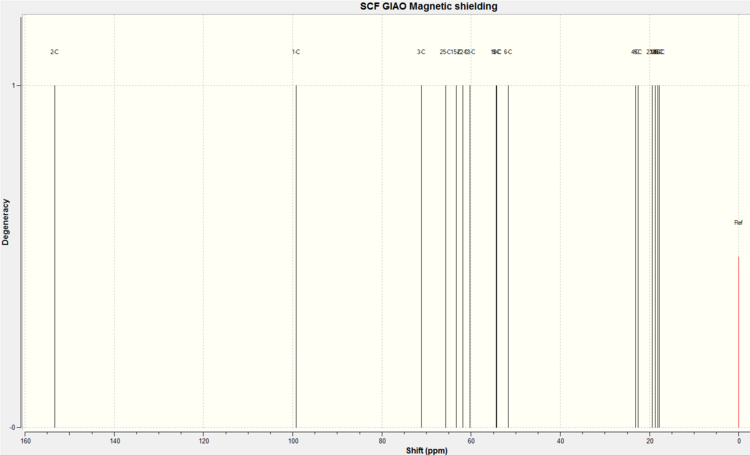
The assignment of the calculated and literature NMR spectra is shown below.
|
|
There are differences between the two chemical shifts values.

Analysis of the NMR data will follow at the end of the NMRs.
NMR of regioisomer 9D
The spectrum produced by the calculations for molecule 9B is shown below.
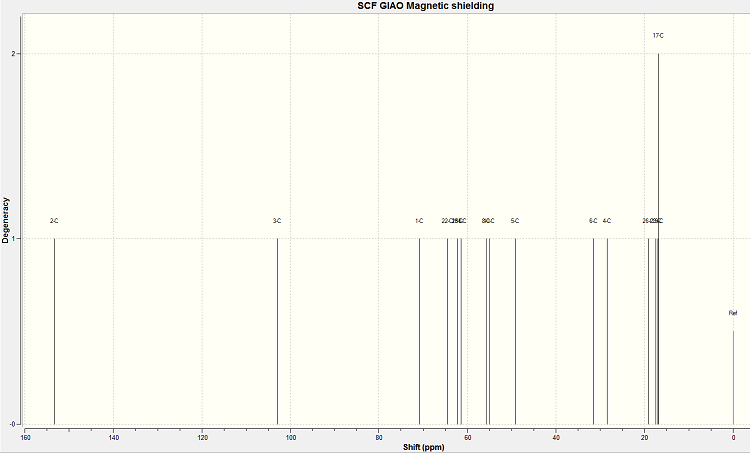
The assignment of the calculated and literature NMR spectra is shown below.
|
|
There are differences between the two chemical shifts values.
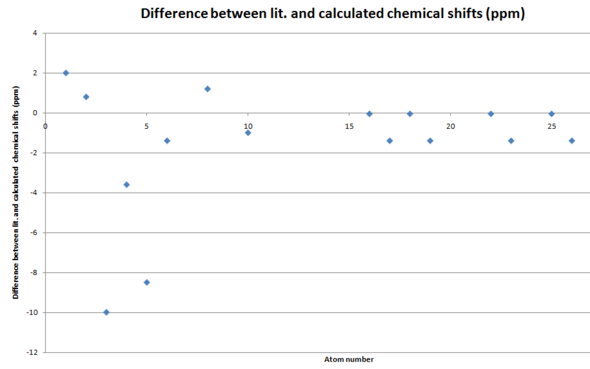
Analysis of the NMR data will follow at the end of the NMRs.
Discussion of NMR data
On initial inspection it is obvious that 9B is a correct assignment, as it is the only predicted spectra that has two peaks in the 140-130ppm region. Both 9C & 9D don't have peaks in that region and instead have only one peak in the +150-110ppm region. This is further backed up by the fact that both 9B's spectra omit peaks at ~100ppm and ~70ppm, which both 9C and 9D have. It is therefore a reasonable conclusion to draw that 9B is the correctly assigned regioisomer.
The NMR data of compounds 9C and 9D is remarkably similar with either Gaussian calculated NMR fitting the literature data to a reasonably good degree. This obviously brings round the issue of how to tell the regioisomers apart. Ruzziconi et al reported the difference between the 9C and 9D regioisomers by carbon-phosphorous coupling. Janocchio method was applied to the JC-P coupling to try and assign the regioisomers but it would appear the Janocchio method is not suitable for "unusual" coupling such as carbon and phosphorous. A more rigorous approach must then be applied using DFT methods and the Gaussian keyword NMR(spinspin). This is displayed on the next section.
At first glance on the difference graphs for all three regioisomers show their largest differences for atoms in the cyclohexene ring, i.e. carbon atoms 1-6. One possible reason for this is that the cyclohexene ring can adopt numerous conformations which are accessible in the NMR timescale, with the carbon atoms have slightly different chemical shifts in each conformation. Therefore, the chemical shifts shown in the literature are actually weighted averages. This would explain the apparent systematic discrepancy for these atoms. A possible improvement for this investigation would be to find several low energy conformers and run the NMR simiulation calculations on each of them, to give a more appropriate value.
Furthermore, the carbon atom bond to the two phosphonate groups had a consistent error of +6.9-8.5ppm. This implies that either the basis set/calculation type is unsuitable for treatment of this or an empirical correction factor should be applied to the heavy phosphorus atom.
Phosphorous-Carbon couplings assignment of the regioisomers
Ruzziconi et al distinguished between the two regioisomers 9C and 9D by the phosphorous carbon couplings of the carbons 3 (green) and 1 (blue) respectively. The 9C 3 carbon is at 73.3ppm is a singlet and the 9D 1 carbon 72.7 clean doublet with J=14.5Hz, the coupling is said to occur with the equatorial phosphorous.
Regioisomer 9C
|
Regioisomer 9D
|
| Regioisomer (Carbon #) |
Lit. Chemical shift |
Calc. Chemical shift |
Lit. carbon phosphorous coupling (Hz) |
Calc. carbon phosphorous 11 coupling (Hz) |
Calc. carbon phosphorous 12 coupling (Hz) |
|---|---|---|---|---|---|
| 9C 3 | 73.3 | 71.1 | Not observed | 4JP(eq)-C =-0.88 | 4JP-C =-0.88 |
| 9D 1 | 72.7 | 70.8 | 3JPC = 14.5 | 3JP(eq)-C = 14.3 | 3JP(ax)-C = 1.00 |
The calculated coupling supports the literature with the information between the two matching to a high degree of accuracy. For example the peak for 9D at 72.7 being split into a doublet of ~14.5Hz. After this initial foray into carbon phosphorous NMR more comparisons between the literature and experimental can be made to check the assertions made.
| Reported coupling lit | Calculated coupling |
|---|---|
| 9C - 3JP-C(2) = 11.3 Hz t | 9C - 3JP-C(2) = 10.5 Hz t |
| 9C- 3JP-C(4) = 10.4 Hz t | 9C - 3JP-C(4) = 4.7 Hz t |
| 9D - 3JP-C(3) = 14.5 Hz t | 9D - 3JP-C(3) = 14.3 Hz t |
| 9D- 3JP-C(1) = 12.6 Hz t | 9D - 3JP-C(1) = 8.7 Hz t |
There is reasonable correlation between the 3JP-C values. This shows that the method is good, but still somewhat limited, more conformations and more detailed calculations could lead to a more accurate analysis of the carbon-phosphorous coupling.
IR comparison of the three regioisomers
The infra-red data provided by Ruzziconi et al can be compared the calculated IR data to help the assignments of regioisomers further.
| Regioisomer | Calculated | Lit. value | Corrected* calc. value |
|---|---|---|---|
| 9B | 1766 | 1652 | 1668 |
| 9C | 1728 | 1655 | 1632 |
| 9D | 1758 | 1654 | 1660 |
*The corrected value is the calculated value multiplied by a factor of 0.944, which was empirical found using linear least squares method.
Unfortunately since the literature values for the three IR's spectrum are so similar no real conclusions can be drawn from them.
Free energy comparison of the three regioisomers
It is reported by Ruzziconi et al that after prolonged heating (240hours at 100oC) only one of the three regioisomers was left, implying that one of the three regioisomers is more thermodynamically stable. Ruzziconi attributed 9C to be the most stable isomer. Using DFT calculations based on first principles the relative energies of the three regioisomers can be calculated.
| Regioisomer | Sum of electronic and thermal Free Energies ( |
|---|---|
| 9B | -1913.176033 |
| 9C | -1913.177028 |
| 9D | -1913.174471 |
The regioisomer with the lowest free energy (and therefore most thermodyanically stable) is 9C according to the DFT calculations. supporting Ruzziconi et al observation that 9C the regioisomer preferred after extended periods of heating.This supports their assignment of regioisomer 9C.
Mechanistic justification of the three regioisomers
Justification of the assignment can be achieved somewhat by considering the mechanism - i.e. the stereospecific nature of the Diels-Alder 4+2 cycloaddition. [22]
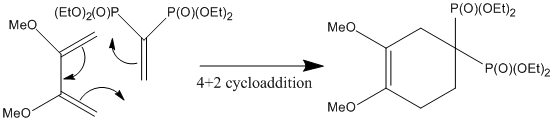
As the above mechanism details there is only one feasible product of this reaction, with the conditions being set as to encourage the cycloaddition (Ruzziconi et al). A more rigorous approach using frontier molecular orbitals could be applied to understand the reaction, but due to the stereospecificity of the mechanism it would not appear to be the case. The regioisomers 9C and 9D also appear in the product, but it is unlikely that they are formed from the reactant but rather by isomerismation of 9B.
Mini-project conclusion
In conclusion, by using a plethora of computational techniques it is possible to assign the regioisomers 9B, 9C and 9D with a fair degree of confidence. 9B can be assigned by it's distinctive NMR compared to 9C and 9D. The 9C and 9D regioisomers can then be told apart by phosphorous carbon coupling of the methoxy substituted alkane carbon. The free energies and IR cannot help this the assignment of the regioisomers. The mechanism can only help assign 9B from 9C and 9D.
Therefore, phosphorous carbon coupling is the one of the way ways to tell the two regioisomers of this potential pharmaceutical apart. This coupling technique is powerful and it's full potential has not been shown here, it could be used to identify many other regioisomers containing phosphorous and other NMR active elements.
References
- ↑ P.J. Jr. Wilson, J.H. Wells, Chem. Rev., 1944, 34, 1
- ↑ K. Alder, G. Stein, Angew. Chem., 1937, 514
- ↑ J. Baldwin, J. Org. Chem., 1966, 2441
- ↑ P. Caramella,P. Quadrelli and L. Toma, J. Am. Chem. Soc., 2002, 1130, DOI:10.1021/ja016622h
- ↑ D. Skála, J. Hanika, Pet. Coal, 2003, 45, 105
- ↑ J. Zoua, X. Zhanga, J. Konga and L. Wang, Fuel, 2008, 3655
- ↑ 7.0 7.1 A. Schultz, L. Flood, J. Springer, J. Org. Chem., 1986, 51, 838; DOI:10.1021/jo00356a016
- ↑ S. Leleu, C. Papamicaël, F. Marsais, G. Dupas and V. Levacher, Tetrahedron: Asymmetry, 2004, 15, 3919
- ↑ G. Bringmann, A.J.P. Mortimer, P.A. Keller, et al, Angew. Chem. Int. Ed., 2005, 44, 5384: DOI:10.1002/anie.200462661
- ↑ S.W. Elmore, L.A. Paquette, Tetrahedron Lett., 1991, 32, 319
- ↑ 11.0 11.1 A. McEwen, P. Schleyer, J. Am. Chem. Soc., 1986, 3951
- ↑ W. Maier, P. Schleyer,J. Am. Chem. SOC., 1981, 1891
- ↑ 13.0 13.1 13.2 13.3 B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447. DOI:10.1039/P29920000447
- ↑ B. Halton, S. Russell, J. Org. Chem., 1991, 5553
- ↑ G. Socrates, Infrared and Raman Characteristic Group Frequencies, 3rd Edition, 2001, p. 65.
- ↑ J. Coates, “Interpretation of Infrared Spectra, A Practical Approach", Encyclopedia of Analytical Chemistry, John Wiley & Sons Ltd, Chichester, 2000
- ↑ Ebetino, F. H.; Dansereau, S. M. In Bisphosphonate Antiresorptive Structure-Activity Relationships; Bijvoet, O. L. M., Fleisch, H. A., Canfield, R. E., Russell, R. G. G., Eds.; Elsevier Science Biomedical: Amsterdam, The Netherlands, 1995; Chapter 9.
- ↑ Geddes, A. D.; D’Souza, S. M.; Ebetino, F. H.; Ibbotson, K. J. Bone and Mineral Research/8; Elsevier Science: New York, 1994.
- ↑ Papaploulos, S. E.; Lanoman, J. O.; Bijvoet, O. L. M.; Lowix, C. W. G. M.; Valkema, R.; Pauwels, E. K. J.; Vermeij, P. Bone, 1992, 13, S41
- ↑ Fleisch, H.; Senn, H.-J. In Bisphosphonates and Tumor- Osteolysis; Brunner, K. W., Fleisch, H., Senn, H.-J., Eds.; Recent Results in Cancer Research; Springer-Verlag: New York, 1989; Vol. 11603.
- ↑ R. Ruzziconi, G. Ricci, A. Gioiello, H. Couthon-Gourvès, and J. Gourvès‡J. Org. Chem., 2003, 736
- ↑ Daniewski, W. M.; Griffin, C. E. J. Org. Chem., 1966, 31, 3236
